How to Find Linear Momentum: A Comprehensive Guide

by

Linear momentum is a fundamental concept in classical mechanics that describes the motion of an object. It is defined as the product of an object’s mass and its velocity, and it is a vector quantity, meaning it has both magnitude and direction. Understanding how to calculate and apply linear momentum is crucial for various fields, including physics, engineering, and even sports analysis.

Understanding the Linear Momentum Equation

The linear momentum equation is expressed as:

$P = m \cdot v$

Where:
– $P$ is the linear momentum of the object
– $m$ is the mass of the object
– $v$ is the velocity of the object

The SI unit for linear momentum is kilogram-meter per second (kg·m/s).

Calculating Linear Momentum

how to find linear momentum

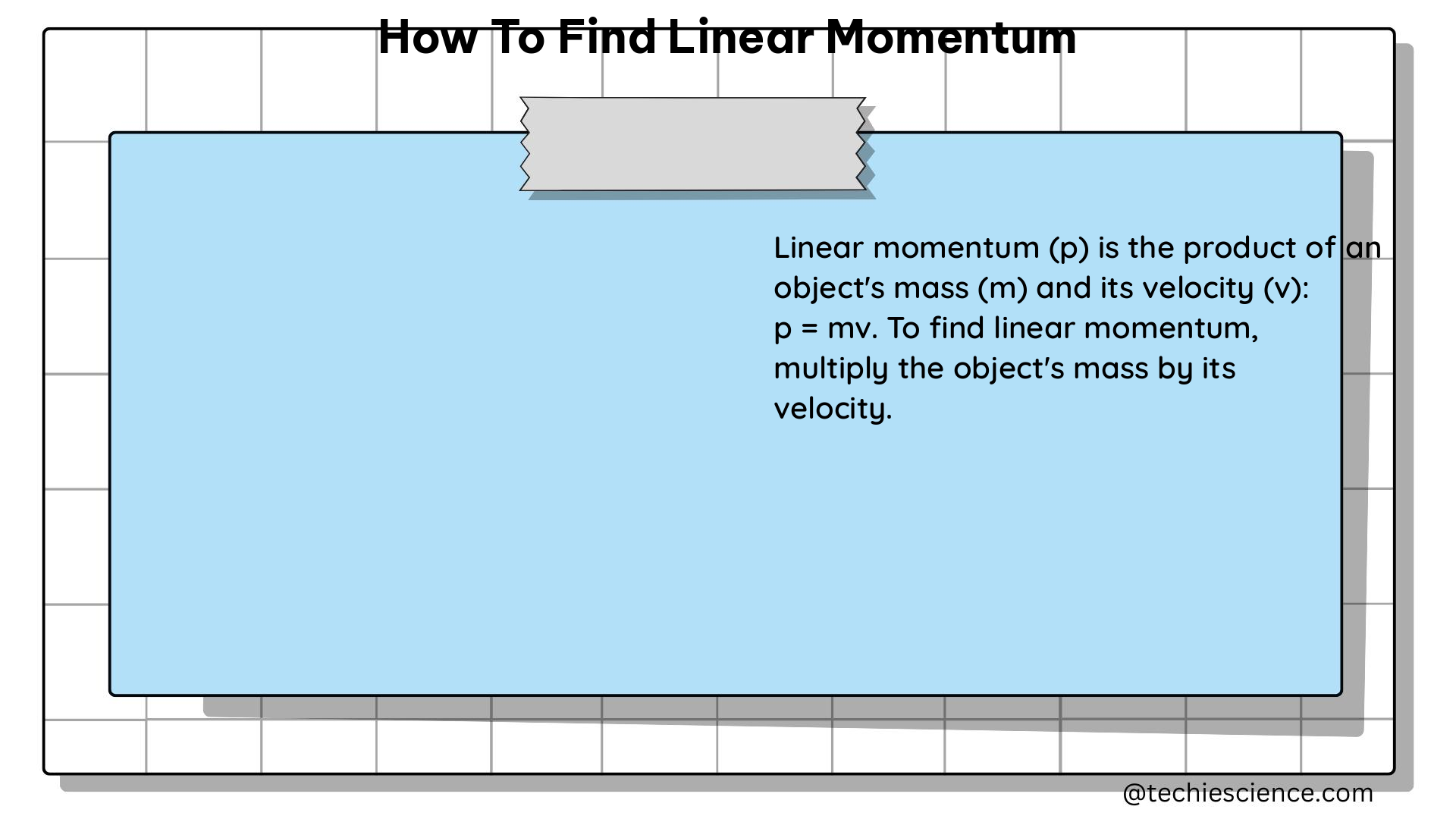
To calculate the linear momentum of an object, you need to know its mass and velocity. Here’s the step-by-step process:

  1. Determine the mass of the object in kilograms (kg).
  2. Measure the velocity of the object in meters per second (m/s).
  3. Multiply the mass and velocity to obtain the linear momentum in kg·m/s.

For example, let’s say you have a 2.5 kg object moving at a velocity of 4.0 m/s. The linear momentum of the object would be:

$P = m \cdot v$
$P = 2.5 \text{ kg} \cdot 4.0 \text{ m/s}$
$P = 10 \text{ kg} \cdot \text{m/s}$

Applying the Linear Momentum Equation

The linear momentum equation can be used in various scenarios, such as:

  1. Calculating the Momentum of an Object: As shown in the previous example, you can use the linear momentum equation to calculate the momentum of an object given its mass and velocity.

  2. Determining the Net Force Acting on an Object: The relationship between linear momentum and force is given by Newton’s second law of motion, which states that the net external force acting on an object is equal to the change in momentum divided by the time over which the change occurs:

$F_{net} = \frac{\Delta P}{\Delta t}$

This equation can be used to find the net force acting on an object if you know the change in its momentum and the time over which the change occurred.

  1. Analyzing Collisions and Impulse: The linear momentum equation is also useful in the analysis of collisions and impulse. The change in momentum of an object during a collision is equal to the impulse applied to the object, which is the product of the net force and the time over which the force is applied.

Examples and Applications

  1. Football Player vs. Football: In the example provided in the original answer, we compared the linear momentum of a football player (110 kg, 8.0 m/s) to the linear momentum of a hard-thrown football (0.410 kg, 25.0 m/s). The player’s momentum was found to be approximately 86 times greater than the football’s momentum.

  2. Airplane Propulsion: In the field of aerospace engineering, the linear momentum equation is used to analyze the behavior of fluid systems, such as in airplane propulsion. Engineers can use the equation to calculate the net force required to change the direction of airflow within the aircraft’s engines, which is crucial for efficient design and control.

  3. Hydraulic Pumps: Similarly, in the design of hydraulic pumps, the linear momentum equation helps engineers calculate the net force required to change the direction of fluid flow, enabling them to optimize the pump’s performance and energy efficiency.

  4. Robotics: In the field of robotics, the linear momentum equation is used to design robots that can perform actions requiring specific forces. By understanding the relationship between momentum and force, engineers can develop robots capable of executing tasks with the necessary precision and control.

Conclusion

Linear momentum is a fundamental concept in classical mechanics that describes the motion of an object. The linear momentum equation, $P = m \cdot v$, allows you to calculate the momentum of an object given its mass and velocity, or to determine the net force acting on an object given the change in its momentum and the time over which the change occurs.

Understanding and applying the linear momentum equation is crucial in various fields, from sports analysis to engineering applications. By mastering the concepts and techniques presented in this guide, you’ll be well-equipped to tackle a wide range of problems involving linear momentum.

References

  1. Linear Momentum Equation: Meaning, Purpose & Applications, StudySmarter, https://www.studysmarter.co.uk/explanations/engineering/engineering-fluid-mechanics/linear-momentum-equation/
  2. 8.1 Linear Momentum and Force, Texas Gateway, https://www.texasgateway.org/resource/81-linear-momentum-and-force
  3. Chapter 8 – Linear Momentum and Collisions, OpenStax College Physics 2e, https://www.theexpertta.com/book-files/OpenStaxCollegePhysics2e/Chapter8.pdf