How to Find Frequency of Transverse Wave
Transverse waves are a fascinating phenomenon in physics, and understanding their frequency is crucial to comprehending their behavior. In this blog post, we will delve into the intricacies of finding the frequency of transverse waves, exploring the foundational concepts, mathematical formulas, practical measurement techniques, and advanced concepts related to frequency and transverse waves. So, let’s dive in!
Understanding the Basics of Transverse Waves
Before we can tackle the concept of frequency, let’s first grasp the basics of transverse waves. In a transverse wave, the oscillations occur perpendicular to the direction of wave propagation. Imagine a rope held at one end while you shake the other end up and down. The wave moves horizontally, while the rope oscillates vertically. This up-and-down motion represents the transverse nature of the wave.
The Role of Frequency in Transverse Waves
Frequency plays a vital role in transverse waves. It refers to the number of complete cycles or oscillations that a wave undergoes in one second. In simpler terms, frequency tells us how many times the wave repeats its pattern per unit of time. For example, if you observe a transverse wave and count 10 complete cycles in one second, the frequency of that wave would be 10 hertz (Hz).
The Importance of Frequency Measurement in Physics
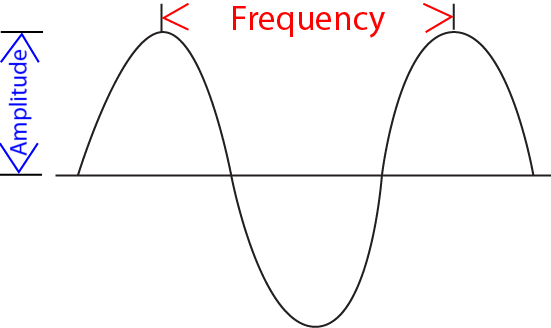
Frequency measurement is of utmost importance in physics, as it helps us understand the characteristics and behavior of transverse waves. By accurately measuring the frequency, we can determine various properties of the wave, such as its speed, wavelength, and amplitude. Additionally, frequency analysis allows us to study wave interference, propagation, reflection, and the energy carried by the wave.
The Mathematical Approach to Finding Frequency of Transverse Waves
Now, let’s delve into the mathematical aspect of finding the frequency of transverse waves. To calculate the frequency, we can use a simple formula:
![]()
Where:
– ![]() represents the frequency of the wave,
represents the frequency of the wave,
– ![]() denotes the wave speed, and
denotes the wave speed, and
– ![]() represents the wavelength of the wave.
represents the wavelength of the wave.
Understanding the Variables in the Frequency Formula
To use the frequency formula effectively, it is essential to understand the variables involved. Wave speed ![]() ) refers to the rate at which the wave propagates through a medium. It is typically measured in meters per second (m/s).
) refers to the rate at which the wave propagates through a medium. It is typically measured in meters per second (m/s).
Wavelength ![]() ), on the other hand, represents the distance between two corresponding points on the wave, such as the crest of one wave to the crest of the next wave or the trough to the trough. It is measured in meters (m).
), on the other hand, represents the distance between two corresponding points on the wave, such as the crest of one wave to the crest of the next wave or the trough to the trough. It is measured in meters (m).
Worked Out Examples: Using the Formula to Calculate Frequency

Let’s put the frequency formula into action with a couple of worked-out examples to solidify our understanding.
Example 1:
Suppose we have a transverse wave traveling through a medium with a speed of 20 m/s and a wavelength of 2 meters. To find the frequency of the wave, we can use the formula:
![]()
Plugging in the given values, we get:
![]()
Simplifying the equation gives us:
![]()
Therefore, the frequency of the transverse wave in this example is 10 Hz.
Example 2:
Let’s consider another scenario where the wave speed is 15 m/s, and the wavelength is 0.5 meters. Applying the frequency formula, we have:
![]()
Simplifying further, we find:
![]()
Hence, the frequency of this transverse wave is 30 Hz.
Practical Approach to Measuring Frequency of Transverse Waves
In real-world applications, measuring the frequency of transverse waves requires appropriate tools and techniques. One commonly used tool is an oscilloscope, which displays the waveform graphically, allowing us to visualize the number of cycles per second. Another technique involves using a frequency counter, a device specifically designed to measure the frequency of a wave accurately.
Step-by-Step Guide to Measure Frequency
If you want to measure the frequency of a transverse wave manually, here is a step-by-step guide you can follow:
- Identify a complete cycle of the transverse wave you wish to measure.
- Start a stopwatch or timer.
- Count the number of complete cycles the wave undergoes within a specific time frame, for example, 10 seconds.
- Divide the number of cycles by the time taken to get the frequency (cycles per second or Hz).
Common Problems and Solutions in Measuring Frequency

While measuring the frequency of transverse waves, you may encounter a few challenges. One common issue is distinguishing complete cycles accurately, especially if the waveform is complex or distorted. To overcome this, it is crucial to carefully observe the wave and identify the points that represent a full cycle. Additionally, external noise or interference can affect the accuracy of measurements. To mitigate this, try conducting measurements in a controlled and quiet environment.
Advanced Concepts Related to Frequency of Transverse Waves
As we delve deeper into the topic, it is essential to explore some advanced concepts related to the frequency of transverse waves:
-
The Impact of Frequency on Wave Properties: The frequency of a transverse wave directly influences its speed, wavelength, and amplitude. Higher frequencies generally correspond to shorter wavelengths and higher speeds, while lower frequencies tend to have longer wavelengths and lower speeds.
-
The Role of Frequency in Wave Interference and Diffraction: Frequency plays a crucial role in wave interference and diffraction phenomena. When two or more waves with different frequencies intersect, they can interfere constructively or destructively, resulting in complex patterns. Similarly, diffraction occurs when waves encounter obstacles or pass through narrow openings, and the frequency determines the extent of diffraction.
-
The Connection between Frequency and Energy of Transverse Waves: The energy of a transverse wave is directly proportional to its frequency. Higher frequency waves carry more energy, while lower frequency waves carry less energy. This relationship between frequency and energy is a fundamental principle in wave physics.
By understanding these advanced concepts, we can gain a deeper insight into the behavior and properties of transverse waves.
Numerical Problems on How to Find Frequency of Transverse Wave
Problem 1:

A transverse wave travels along a string with a speed of 30 m/s. The wavelength of the wave is 0.5 m. Find the frequency of the wave.
Solution:
Given:
Wave speed, ![]() ,
,
Wavelength, ![]()
The formula to find the frequency of a wave is given by:
![]()
Substituting the given values, we get:
![]()
Simplifying the equation:
![]()
Therefore, the frequency of the wave is 60 Hz.
Problem 2:
A transverse wave is produced on a string with a frequency of 200 Hz. If the wave speed is 40 m/s, find the wavelength of the wave.
Solution:
Given:
Frequency, ![]() ,
,
Wave speed, ![]()
The formula to find the wavelength of a wave is given by:
![]()
Substituting the given values, we get:
![]()
Simplifying the equation:
![]()
Therefore, the wavelength of the wave is 0.2 m.
Problem 3:

A transverse wave has a wavelength of 1 m and a frequency of 50 Hz. Find the wave speed.
Solution:
Given:
Wavelength, ![]() ,
,
Frequency, ![]()
The formula to find the wave speed is given by:
![]()
Substituting the given values, we get:
![]()
Simplifying the equation:
![]()
Therefore, the wave speed is 50 m/s.
Also Read:
- How to find the frequency of a wave
- How to find horizontal velocity without time
- How to find wavelength of transverse wave
- How to find horizontal velocity of a projectile
- How to find the amplitude of a wave
- How to find distance in velocity time graph
- How to find velocity with acceleration and time
- How to find velocity without time
- How to find molar mass from volume
- How to find angular acceleration of a wheel
I am Sakshi Sharma, I have completed my post-graduation in applied physics. I like to explore in different areas and article writing is one of them. In my articles, I try to present physics in most understanding manner for the readers.