How to Find Acceleration in Velocity-Time Graph
Understanding the Basics of Velocity-Time Graph
When studying the motion of an object, it is often helpful to analyze its velocity as a function of time. A velocity-time graph, also known as a V-T graph, provides a graphical representation of an object’s velocity over a specific time interval. The graph consists of a horizontal time axis and a vertical velocity axis. By examining the shape and characteristics of the graph, we can gain valuable insights into the object’s motion.
In a velocity-time graph, the slope of the line represents the object’s acceleration. Acceleration is the rate at which an object’s velocity changes over time. It indicates how quickly the object is speeding up or slowing down. When the velocity-time graph has a straight line, the acceleration is constant. A steeper slope indicates a higher acceleration, while a shallower slope represents a lower acceleration.
Importance of Acceleration in Velocity-Time Graph
Acceleration is a fundamental concept in physics that helps us understand the changes in an object’s motion. By examining the acceleration in a velocity-time graph, we can determine whether an object is accelerating, decelerating, or moving at a constant velocity. This information is crucial for analyzing various physical phenomena, including the motion of vehicles, projectiles, and celestial bodies.
Calculating the acceleration in a velocity-time graph allows us to quantify the rate at which an object’s velocity is changing. This information helps us predict an object’s future motion, determine the forces acting upon it, and analyze its overall dynamics.
Steps to Calculate Acceleration in Velocity-Time Graph
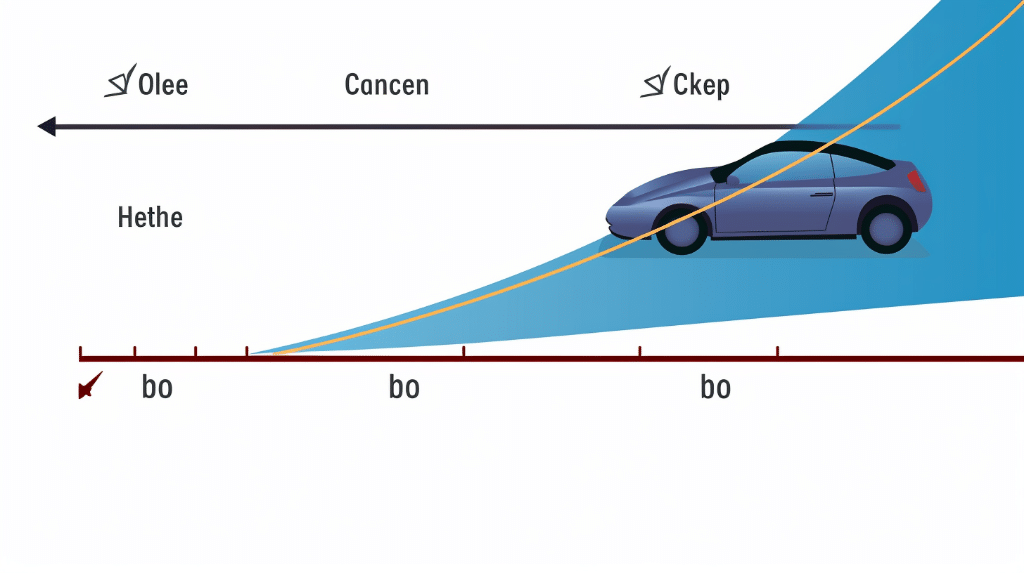
To calculate acceleration using a velocity-time graph, follow these steps:
1. Identifying Key Points on the Graph
Examine the velocity-time graph and identify two key points: the initial velocity (vi) and the final velocity (vf). The initial velocity represents the object’s velocity at the beginning of the time interval, while the final velocity represents its velocity at the end of the interval.
2. Using the Slope Formula to Calculate Acceleration
The slope of the velocity-time graph represents the object’s acceleration. To calculate the slope, we use the formula:
![]()
where vf is the final velocity, vi is the initial velocity, and t is the time interval.
3. Interpreting the Results
Once you have calculated the acceleration using the slope formula, you can interpret the results. A positive acceleration indicates that the object is speeding up, while a negative acceleration indicates that it is slowing down. If the acceleration is zero, the object is moving at a constant velocity.
Worked Out Examples
Let’s work through a few examples to solidify our understanding of calculating acceleration in velocity-time graphs.
Example of a Positive Acceleration
Suppose we have a velocity-time graph that shows a straight line with a positive slope. The initial velocity (vi) is 10 m/s, the final velocity (vf) is 30 m/s, and the time interval (t) is 5 seconds.
Using the slope formula, we can calculate the acceleration:
![]()
Therefore, the object has a positive acceleration of 4 m/s^2, indicating that it is speeding up.
Example of a Negative Acceleration
Now let’s consider a velocity-time graph with a negative slope. The initial velocity (vi) is 20 m/s, the final velocity (vf) is 10 m/s, and the time interval (t) is 2 seconds.
Using the slope formula:
![]()
In this case, the object has a negative acceleration of -5 m/s^2, indicating that it is slowing down.
Example of Zero Acceleration
Finally, let’s examine a velocity-time graph with a horizontal line. This line represents a constant velocity. If the initial velocity (vi) is 15 m/s, the final velocity (vf) is also 15 m/s, and the time interval (t) is 4 seconds, the acceleration will be zero.
Using the slope formula:
![]()
The object has a zero acceleration, indicating that its velocity remains constant.
Common Misconceptions in Calculating Acceleration in Velocity-Time Graph
While calculating acceleration in a velocity-time graph, it is crucial to avoid common misconceptions. Let’s address a few of them:
Misconception about the Slope
Some people may mistakenly assume that the slope of a velocity-time graph represents the velocity instead of the acceleration. Remember, the slope represents the change in velocity over time, which gives us the acceleration.
Misconception about the Area under the Graph
Another misconception is that the area under a velocity-time graph directly provides the acceleration. However, the area under the graph represents the displacement or distance traveled, not the acceleration.
Misconception about the Time Interval
People sometimes assume that the time interval for calculating acceleration should be the entire duration of the graph. However, the time interval should only include the specific segment for which you want to calculate the acceleration.
Understanding how to find acceleration in a velocity-time graph is essential for analyzing an object’s motion. By identifying key points on the graph and using the slope formula, we can determine the acceleration and gain valuable insights into the object’s dynamics. Remember to be aware of common misconceptions to ensure accurate calculations.
How can we find acceleration and velocity using velocity-time graphs and constant acceleration?
To understand the concept of finding acceleration and velocity using velocity-time graphs and constant acceleration, we can explore the article on How to Find Acceleration in Velocity-Time Graph. This article provides a comprehensive explanation of the steps involved in determining acceleration from a velocity-time graph. Additionally, to understand the connection between acceleration and velocity, you can refer to the article on Finding Velocity with Constant Acceleration. This article elucidates the process of calculating velocity when the acceleration remains constant. By integrating these two concepts, we can gain a deeper understanding of the relationship between velocity and acceleration in dynamic systems.
Numerical Problems on how to find acceleration in velocity time graph
Problem 1:
A car accelerates uniformly from rest to a velocity of 40 m/s in 10 seconds. Find the acceleration of the car.
Solution:
Given:
Initial velocity, ![]()
Final velocity, ![]()
Time taken, ![]()
The acceleration (![]() ) can be found using the formula:
) can be found using the formula:
![]()
Substituting the given values, we have:
![]()
Simplifying the equation, we get:
![]()
Therefore, the acceleration of the car is ![]() .
.
Problem 2:
A train starts from rest and accelerates uniformly. It covers a distance of 200 m in 10 seconds. Find the acceleration of the train.
Solution:
Given:
Initial velocity, ![]()
Distance covered, ![]()
Time taken, ![]()
The acceleration (![]() ) can be found using the formula:
) can be found using the formula:
![]()
Substituting the given values, we have:
![]()
Simplifying the equation, we get:
![]()
Therefore, the acceleration of the train is ![]() .
.
Problem 3:
A particle is moving with a constant acceleration. Its initial velocity is 10 m/s and it covers a distance of 100 m in 5 seconds. Find the acceleration of the particle.
Solution:
Given:
Initial velocity, ![]()
Distance covered, ![]()
Time taken, ![]()
The acceleration (![]() ) can be found using the formula:
) can be found using the formula:
![]()
Substituting the given values, we have:
![]()
Simplifying the equation, we get:
![]()
Therefore, the acceleration of the particle is ![]() .
.
Also Read:
- How to determine velocity in quantum decoherence
- Find coefficient of friction given velocity and distance
- How to find final velocity
- How to find velocity of ultrasonic waves
- How to calculate mass from force and velocity
- How to calculate velocity of a wave on a string
- How does position change velocity
- Is angular velocity negative
- How to find velocity between two points
- How to find velocity vector
Hi, I’m Akshita Mapari. I have done M.Sc. in Physics. I have worked on projects like Numerical modeling of winds and waves during cyclone, Physics of toys and mechanized thrill machines in amusement park based on Classical Mechanics. I have pursued a course on Arduino and have accomplished some mini projects on Arduino UNO. I always like to explore new zones in the field of science. I personally believe that learning is more enthusiastic when learnt with creativity. Apart from this, I like to read, travel, strumming on guitar, identifying rocks and strata, photography and playing chess.