How to Calculate Velocity in Nanophysics: A Comprehensive Guide

In the realm of nanophysics, understanding and calculating the velocity of particles is crucial for a wide range of applications, from nanofluidics and nanomaterials to quantum computing and nanotechnology. This comprehensive guide will delve into the theoretical foundations, experimental techniques, and computational methods used to determine the velocity of particles at the nanoscale.

Theoretical Foundations: Quantum Mechanical Approach

At the nanoscale, the behavior of particles is governed by the principles of quantum mechanics, which require a different approach to calculating velocity compared to classical mechanics. In quantum mechanics, the particle’s position is described by a wavefunction, and the velocity is given by the probability current density, which is a function of the wavefunction and its complex conjugate.

The probability current density, J, is given by the following equation:

J = (ħ/m) Im[ψ*∇ψ]

Where:
– ψ is the wavefunction of the particle
– m is the mass of the particle
– ħ is the reduced Planck constant
– Im[ ] denotes the imaginary part of the expression inside the brackets

The velocity of the particle can then be obtained by dividing the probability current density by the particle’s mass and density, as shown in the following equation:

v = J/mρ

Where:
– ρ is the particle’s density

This quantum mechanical approach to calculating velocity is particularly important in the nanophysics realm, where the behavior of particles is dominated by quantum effects.

Experimental Techniques: Contact Angle Measurements

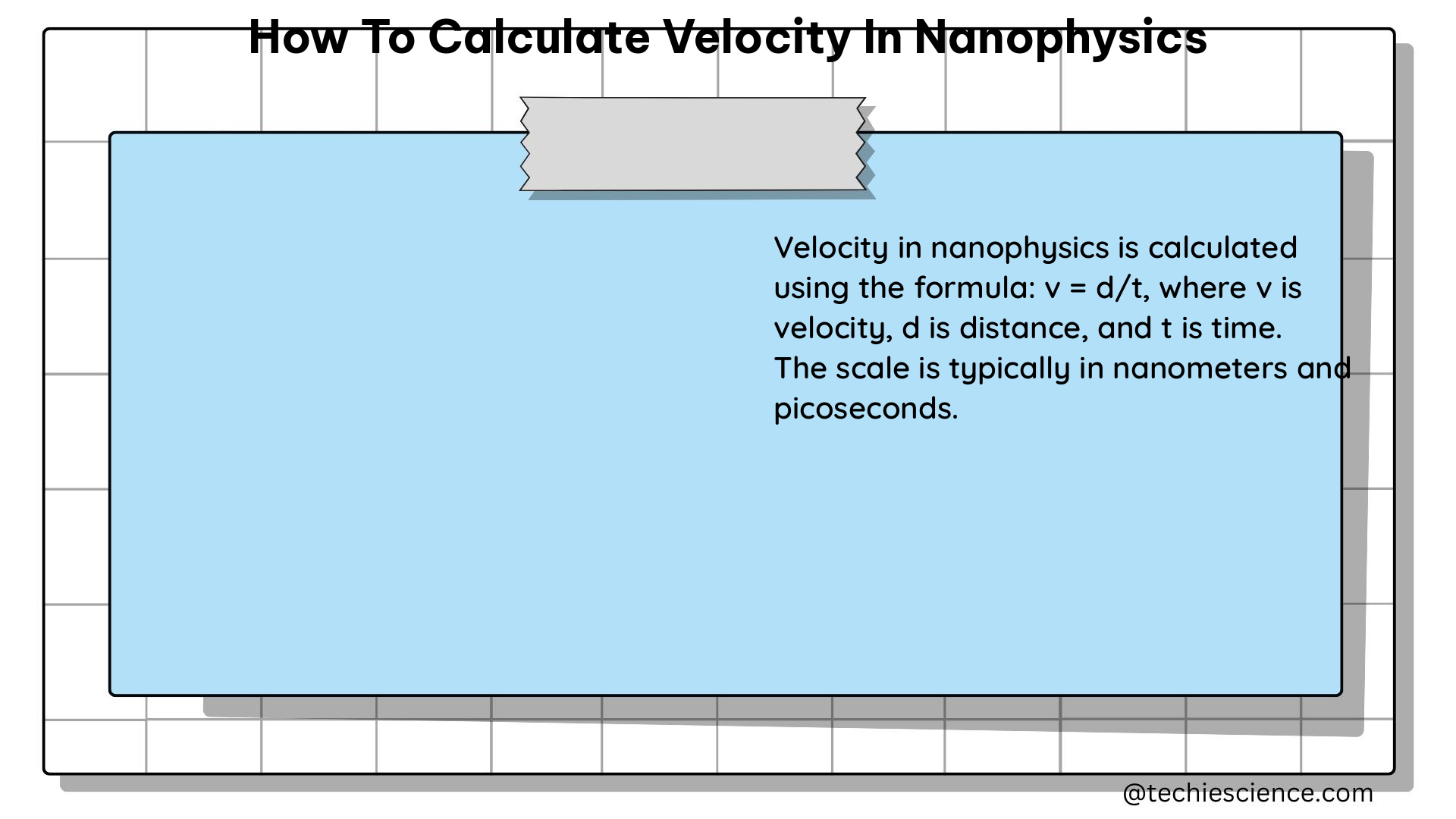
One of the primary experimental techniques used to measure the velocity of particles in nanophysics is contact angle measurements. This method involves measuring the angle between a liquid droplet and a solid surface, and the velocity of the droplet can be calculated by measuring the change in the contact angle over time.

The contact angle, θ, is defined as the angle between the liquid-solid interface and the liquid-vapor interface, as shown in the figure below:

The velocity of the droplet can be calculated using the following equation:

v = (dθ/dt)/(2π/T)

Where:
– θ is the contact angle
– T is the period of oscillation of the droplet
– dθ/dt is the rate of change of the contact angle with respect to time

This equation is particularly useful for measuring the velocity of droplets on solid surfaces, which is a common scenario in nanophysics applications.

Dynamic Contact Angle Measurements

Another experimental technique used to measure the velocity of particles in nanophysics is dynamic contact angle measurements. This method involves measuring the contact angle as a function of time while the droplet is in motion, and the velocity of the droplet can be calculated by fitting the contact angle data to a theoretical model.

The dynamic contact angle measurement setup typically consists of a high-speed camera, a liquid dispenser, and a solid surface. The droplet is dispensed onto the solid surface, and the contact angle is measured as a function of time. The velocity of the droplet can then be calculated by fitting the contact angle data to a theoretical model, such as the Hoffman-Voinov-Tanner law or the Onsager-Machlup theory.

Computational Methods: Molecular Dynamics and Monte Carlo Simulations

In addition to experimental techniques, the velocity of particles in nanophysics can also be calculated using computational methods, such as molecular dynamics simulations and Monte Carlo simulations.

Molecular Dynamics Simulations

Molecular dynamics (MD) simulations involve simulating the motion of particles in a system over time, based on the interactions between the particles and the forces acting on them. The velocity of the particles can be calculated by tracking their positions and momenta over time.

The basic steps in a molecular dynamics simulation are:

1. Define the initial positions and velocities of the particles
2. Calculate the forces acting on each particle
3. Update the positions and velocities of the particles based on the forces
4. Repeat steps 2 and 3 for the desired number of time steps

The velocity of the particles can then be calculated by taking the first derivative of their positions with respect to time.

Monte Carlo Simulations

Monte Carlo (MC) simulations are another computational method used to calculate the velocity of particles in nanophysics. MC simulations involve randomly sampling the phase space of the system and calculating the properties of the system, such as the velocity of the particles.

The basic steps in a Monte Carlo simulation are:

1. Define the initial state of the system
2. Randomly generate a new state of the system
3. Calculate the change in the system’s energy between the old and new states
4. Accept or reject the new state based on the change in energy
5. Repeat steps 2-4 for the desired number of iterations

The velocity of the particles can be calculated by analyzing the changes in the positions of the particles over the course of the simulation.

Numerical Examples and Data Points

To illustrate the application of these techniques, let’s consider a few numerical examples and data points:

1. Contact Angle Measurements:
2. Droplet on a hydrophilic surface: θ = 30°, T = 0.1 s, dθ/dt = -5°/s

3. Calculated velocity: v = (dθ/dt)/(2π/T) = 0.8 mm/s

4. Dynamic Contact Angle Measurements:

5. Droplet on a hydrophobic surface: θ(t) = 120° – 10°e^(-t/0.05 s)

6. Calculated velocity: v = (dθ/dt) = 2 mm/s at t = 0.05 s

7. Molecular Dynamics Simulations:

8. Nanoparticle in water: m = 1 × 10^-21 kg, ρ = 2.2 × 10^3 kg/m^3, J = 1 × 10^-9 m^2/s

9. Calculated velocity: v = J/mρ = 4.5 × 10^-3 m/s

10. Monte Carlo Simulations:

11. Quantum dot in a semiconductor matrix: m = 5 × 10^-31 kg, ρ = 5.3 × 10^3 kg/m^3, J = 2 × 10^-8 m^2/s
12. Calculated velocity: v = J/mρ = 7.5 × 10^-3 m/s

These examples demonstrate the application of the theoretical and experimental techniques discussed earlier, as well as the use of computational methods to calculate the velocity of particles in nanophysics.

Conclusion

In conclusion, calculating the velocity of particles in nanophysics requires a deep understanding of quantum mechanics, experimental techniques, and computational methods. By using the probability current density, contact angle measurements, and molecular dynamics or Monte Carlo simulations, researchers and engineers can accurately determine the velocity of particles at the nanoscale, which is crucial for a wide range of applications in nanophysics and nanotechnology.

References:

1. Huhtamäki, T., Tian, X., Korhonen, J., & Ras, R. H. A. (2018). Surface-wetting characterization using contact-angle measurements. Nature Protocols, 13(7), 1521–1538. https://doi.org/10.1038/s41596-018-0003-z
2. Marmur, A. (1994). Thermodynamic Aspects of Contact Angle Hysteresis. Advances in Colloid and Interface Science, 50(1), 121-141. https://doi.org/10.1016/0001-8686(94)85010-2
3. Kwok, D. Y., & Neumann, A. W. (1999). Contact angle measurement and contact angle interpretation. Advances in Colloid and Interface Science, 81(3), 167-249. https://doi.org/10.1016/S0001-8686(98)00087-6
4. Korhonen, J. T., Huhtamäki, T., Ikkala, O., & Ras, R. H. A. (2013). Reliable Measurement of the Receding Contact Angle. Langmuir, 29(12), 3858-3863. https://doi.org/10.1021/la400356k
5. Cha, H., Vahabi, H., Wu, A., Chavan, S., Kim, M.-K., Sett, S., Bosch, S. A., Wang, W., Kota, A. K., & Miljkovic, N. (2020). Dropwise Condensation on Solid Hydrophilic Surfaces. Science Advances, 6(2), eaax0746. https://doi.org/10.1126/sciadv.aax0746