Flexural Strength: 13 Interesting Facts To Know

Content

Flexural strength

“Flexural strength (σ), also acknowledged as Modulus of rupture, or bend strength, or transverse rupture strength, is a property of material, well-defined as the material stress just before it yields in a flexure test. A sample ( circular/ rectangular cross-section) is bent until fracture or yielding using a 3 point flexural testing. The flexural strength signifies the highest stress applied at the moment of yielding.”

Flexural strength definition

flexural strength can be defined as the normal stress generated in the material because of the member’s bending or flexing in a flexure test. It is evaluated by employing a three-point bending method in which a specimen of a circular or rectangular cross-section is yielding till fractured. It is the Maximum stress experienced at the yield point by that materials.

Flexural strength formula | Flexural strength unit

Assume a rectangular specimen under a Load in 3 – point bending setup:

$\\sigma=\\frac{3WL}{2bd^2}$

Where W is the force at the point of fracture or failure

L is the distance between the supports

b is the width of the beam

d is the thickness of the beam

The unit of flexural strength is MPa, Pa etc.

Similarly, in 4 – point bending setup where the loading span is half of the support span

$\\sigma=\\frac{3WL}{4bd^2}$

Similarly, in 4 – point bending setup where loading span is 1/3 of the support span

$\\sigma=\\frac{WL}{bd^2}$

Flexural strength test

This test produces tensile stress on the specimen’s convex side and Compressive stress on the opposite side. The span to depth ratio is controlled to minimize the shear stress-induced. For most material L/d ratio is equal to 16 is considered.

In comparison with the three-point bending flexural test, Four-point bending flexural test observes No shear forces in the area between the two loading pins. Thus, The four-point bending test is most appropriate for brittle materials that cannot bear shear stresses.

Three-Point Bend test and Equations

Equivalent Point Load wL will act at the centre of the beam. i.e., at L/2

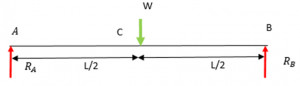
The value of the reaction at A and B can be calculated by applying Equilibrium conditions of

$\\sum F_x=0, \\sum F_y=0, \\sum M_A=0$

For vertical Equilibrium,

$\\sum F_y=0$

$R_A+R_B = W.............[1]$

Taking a moment about A, Clockwise moment positive, and Counter Clockwise moment is taken as negative

$W*(L/2) - R_B*L = 0$

$R_B=\\frac{W}{2}$

Putting the value of R_B in [1], we get

$\\\\R_A=W-R_B\\\\ \\\\R_A=W-\\frac{W}{2}\\\\ \\\\R_A=\\frac{W}{2}$

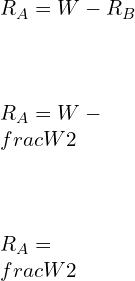
Following the Sign convention for S.F.D. and BMD

Shear Force at A

$V_A=R_A=\\frac{W}{2}$

Shear Force at C

$\\\\V_C=R_A-\\frac{W}{2}\\\\ \\\\V_C=\\frac{W}{2}-\\frac{W}{2}=0$

Shear Force at B

$\\\\V_B=R_B=-\\frac{W}{2}$

For Bending Moment Diagram, if we start calculating Bending Moment from the Left side or Left end of the beam, Clockwise Moment is taken as positive. Counter Clockwise Moment is taken as Negative.

Bending Moment at A = M_A = 0

Bending Moment at C

$\\\\M_C=M_A-\\frac{W}{2}*\\frac{L}{2} \\\\ \\\\M_C= 0-\\frac{WL}{4}\\\\ \\\\M_C=\\frac{-WL}{4}$

Bending Moment at B = 0

In 3 – point bending setup, Flexural strength is given by

$\\sigma=\\frac{3WL}{2bd^2}$

Where W is the force at the point of fracture or failure

L is the distance between the supports

b is the width of the beam

d is the thickness of the beam

The unit of flexural strength is MPa, Pa etc.

Four-Point Bend test and Equations

Consider a simply supported beam with two equal Loads W acting at a distance L/3 from either end.

The value of the reaction at A and B can be calculated by applying Equilibrium conditions of

$\\sum F_x=0, \\sum F_y=0, \\sum M_A=0$

For vertical Equilibrium,

$\\sum F_y=0$

$R_A+R_B = W.............[1]$

Taking a moment about A, Clockwise moment positive, and Counter Clockwise moment is taken as negative

$W*[L/6] - R_B*L = W[L/3]$

$R_B=\\frac{W}{2}$

Putting the value of R_B in [1], we get

$\\\\R_A=W-R_B\\\\ \\\\R_A=W-\\frac{W}{2}\\\\ \\\\R_A=\\frac{W}{2}$

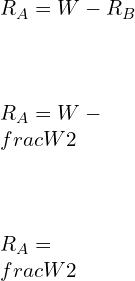
Following the Sign convention for S.F.D. and BMD

Shear Force at A

$V_A=R_A=\\frac{W}{2}$

Shear Force at C

$\\\\V_C=R_A-\\frac{W}{2}\\\\ \\\\V_C=\\frac{W}{2}-\\frac{W}{2}=0$

Shear Force at B

$\\\\V_B=R_B=-\\frac{W}{2}$

Bending Moment at A = M_A = 0

Bending Moment at C = [W/2]*[L/3]………………………… [since the moment is counter-clockwise, the bending moment is coming out as negative]

Bending Moment at C =

$\\\\M_C=\\frac{WL}{6}$

Bending Moment at D =

$M_D=\\frac{W}{2}*\\frac{2L}{3}-\\frac{W}{2}*\\frac{L}{3}$

$M_D=\\frac{WL}{6}$

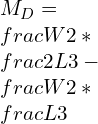
Bending Moment at B = 0

For a rectangular specimen under in 4 – point bending setup:

Similarly, when the loading span is 1/3 of the support span

$\\sigma=\\frac{WL}{bd^2}$

In 4 – point bending setup where the loading span is half of the support span

$\\sigma=\\frac{3WL}{4bd^2}$

Where W is the force at the point of fracture or failure

L is the distance between the supports

b is the width of the beam

d is the thickness of the beam

The unit of flexural strength is MPa, Pa etc.

Flexural strength vs Flexural Modulus

Flexural Modulus is a ratio of stress-induced during flexural bending to the strain during flexing deformation. It is the property or the ability of the material to resist bending. In comparison, flexural strength can be defined as the normal stress generated in the material because of the member’s bending or flexing in a flexure test. It is evaluated employing the Three-point bending method in which a specimen of a circular or rectangular cross-section is bent until fracture or yielding. It is the Maximum stress experienced by the material at the yield point.

Assume a rectangular cross-section beam made of isotropic material, W is the force applied at the middle of the beam, L is the beam’s length, b is the beam’s width, d is the thickness of the beam. δ be a deflection of the beam

For 3 – point bending setup:

Flexural Modulus can be given by

$E_{bend}=\\frac{\\sigma }{\\epsilon }$

$E_{bend}=\\frac{WL^3 }{4bd^3\\delta }$

for a simply supported beam with load at the centre, the deflection of the beam can be given by

$\\delta =\\frac{WL^3}{48EI}$

Flexural strength vs Tensile strength

Tensile strength is the maximum tensile stress a material can withstand under tensile loading. It is the property of the material. It is independent of the shape of the specimen. It gets affected by the thickness of the material, notches, internal crystal structures etc.

Flexural strength is not the property of the material. It is the normal stress generated in the material because of the member’s bending or flexing in a flexure test. It is dependent upon the size and shape of the specimen. The following example will explain further:

Consider a square cross-section beam and a diamond cross-section beam with sides ‘a’ and bending moment M

For a square cross-section beam

By Euler-Bernoulli’s Equation

$\\\\M=\\frac{\\sigma I/y}{y}\\\\ \\\\Z=\\frac{I}{y}\\\\ \\\\M_1=\\frac{\\sigma _1 a^3}{6}$

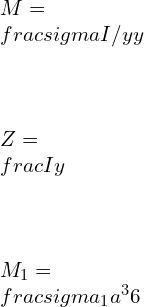
For a Diamond cross-section beam

$\\\\I=\\frac{bd^3}{12}*2\\\\ \\\\I=\\sqrt{2}a*[\\frac{a}{\\sqrt{2}}]^3*\\frac{2}{12}\\\\\\\\ \\\\Z=\\frac{I}{y}=\\frac{a^3}{6\\sqrt{a}}\\\\\\\\ \\\\M_2=\\frac{\\sigma _2 a^3}{6\\sqrt{a}}$

But M₁ = M₂

$\\\\\\frac{\\sigma _1 a^3}{6}=\\frac{\\sigma _2 a^3}{6\\sqrt{a}} \\\\\\\\\\sigma _2= \\sqrt{2}\\sigma _1 \\\\\\sigma _2>\\sigma _1$

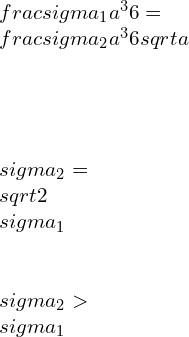
Flexural strength of Concrete

Procedure for evaluating Flexure Strength of Concrete

Consider any desired grade of Concrete and prepare an unreinforced specimen of dimensions 12in x 4 in x 4 in. Cure the prepared solution for 26-28 days.
Before performing the Flexure test, Allow the specimen to rest in the water at 25 C for 48 hours.
Immediately perform the bend test on the specimen while it is in wet condition. [Quickly after removing the specimen from the water]
To indicate the roller support position, draw a reference line at 2 inches from both the edges of the specimen.
The roller supports act as a simply supported beam. Gradual application of load is made on the axis of the beam.
The load is increased continuously until the stress in the extreme fiber of the beam increases at the rate of 98 lb./sq. in/min.
The load is continuously applied until the test specimen breaks, and the maximum load value is recorded.

In 3 – point bending setup, Flexural strength is given by

$\\sigma=\\frac{3WL}{2bd^2}$

Where W is the force at the point of fracture or failure

L is the distance between the supports

b is the width of the beam

d is the thickness of the beam

The unit of flexural strength is MPa, Pa etc.

Flexural strength is nearly = 0.7 times the compressive strength of the Concrete.

Flexural strength of steel

Consider a steel beam with width = 150 mm, depth = 150 mm, and length = 700 mm, applied load be 50 kN, and find the beam’s flexural stress of the beam?

In 3 – point bending setup, Flexural stress is given by

$\\\\\\sigma=\\frac{3WL}{2bd^2} \\\\\\\\\\sigma=\\frac{3*50*10^3*0.7}{2*0.15*0.15^2} \\\\\\\\\\sigma=15.55\\;MPa$

Flexural strength of Aluminum

The flexural strength of Aluminum grade 6061 is 299 MPa.

Flexural strength of Wood

The following table shows the flexural strength of the various type of woods.

Type of Wood	Flexural strength [MPa]
Alder	67.56 MPa
Ash	103.42 MPa
Aspen	57.91 MPa
Basswood	59.98 MPa
Beech	102.73 MPa
Birch, Yellow	114.45 MPa
Butternut	55.84 MPa
Cherry	84.80 MPa
Chestnut	59.29 MPa
Elm	81.35 MPa
Hickory	139.27 MPa

Flexural strength of a Cylinder

Consider a simply supported beam with two equal Loads W/2 acting at a distance L/3 from either end.

The value of the reaction at A and B can be calculated by applying Equilibrium conditions of

$\\sum F_x=0, \\sum F_y=0, \\sum M_A=0$

For vertical Equilibrium,

$\\sum F_y=0$

$R_A+R_B = W.............[1]$

Taking a moment about A, Clockwise moment positive, and Counter Clockwise moment is taken as negative

$W*[L/6] - R_B*L = W[L/3]$

$R_B=\\frac{W}{2}$

Putting the value of R_B in [1], we get

$\\\\R_A=W-R_B\\\\ \\\\R_A=W-\\frac{W}{2}\\\\ \\\\R_A=\\frac{W}{2}$

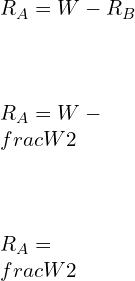
Following the Sign convention for S.F.D. and BMD

Shear Force at A

$V_A=R_A=\\frac{W}{2}$

Shear Force at C

$\\\\V_C=R_A-\\frac{W}{2}\\\\ \\\\V_C=\\frac{W}{2}-\\frac{W}{2}=0$

Shear Force at B

$\\\\V_B=R_B=-\\frac{W}{2}$

Bending Moment at A = M_A = 0

Bending Moment at C = [W/2]*[L/3]………………………… [since the moment is counter-clockwise, the bending moment is coming out as negative]

Bending Moment at C =

$\\\\M_C=\\frac{WL}{6}$

Bending Moment at D =

$M_D=\\frac{W}{2}*\\frac{2L}{3}-\\frac{W}{2}*\\frac{L}{3}$

$M_D=\\frac{WL}{6}$

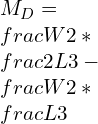
Bending Moment at B = 0

Let d = diameter of the cylindrical beam, According to Euler-Bernoulli’s Equation

$\\\\\\sigma =\\frac{My}{I}\\\\ \\\\I=\\frac{\\pi}{64}d^4, \\\\\\\\y=d/2 \\\\\\\\\\sigma =\\frac{1.697WL}{d^3}$

Find the Flexural stress in the circular cylindrical beam with span of 10 m and diameter 50 mm. The beam is made of Aluminum. Compare the result with beam of square cross section with side = 50 mm. The total load applied is 70 N.

Consider a simply supported beam with two equal Loads W/2 = 35 N acting at a distance L/3 from either end.

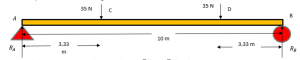
The value of the reaction at A and B can be calculated by applying Equilibrium conditions of

$\\sum F_x=0, \\sum F_y=0, \\sum M_A=0$

For vertical Equilibrium,

$\\sum F_y=0$

$R_A+R_B = 70.............[1]$

Taking a moment about A, Clockwise moment positive, and Counter Clockwise moment is taken as negative

$W*[L/6] - R_B*L = W[L/3]$

$R_B=\\frac{W}{2}=35$

Putting the value of R_B in [1], we get

$\\\\R_A=W-R_B\\\\ \\\\R_A=W-\\frac{W}{2}\\\\ \\\\R_A=70-35=35N$

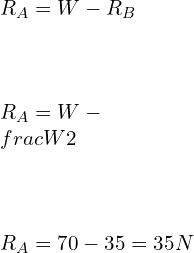
Following the Sign convention for S.F.D. and BMD

Shear Force at A

$V_A=R_A=\\frac{W}{2}=35 N$

Shear Force at C

$\\\\V_C=R_A-\\frac{W}{2}\\\\ \\\\V_C=\\frac{W}{2}-\\frac{W}{2}=0$

Shear Force at B

$\\\\V_B=R_B=-\\frac{W}{2}=-35N$

Bending Moment at A = M_A = 0

Bending Moment at C = [W/2]*[L/3]………………………… [since the moment is counter-clockwise, the bending moment is coming out as negative]

Bending Moment at C =

$\\\\M_C=\\frac{WL}{6}=\\frac{70*10}{6}=125\\;Nm$

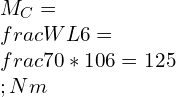
Bending Moment at D =

$M_D=\\frac{W}{2}*\\frac{2L}{3}-\\frac{W}{2}*\\frac{L}{3}$

$M_D=\\frac{WL}{6}=\\frac{70*10}{6}=125\\;Nm$

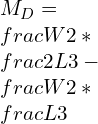
Bending Moment at B = 0

Let d = diameter of the cylindrical beam, According to Euler-Bernoulli’s Equation

$\\\\\\sigma =\\frac{My}{I}\\\\ \\\\I=\\frac{\\pi}{64}d^4=\\frac{\\pi}{64}*0.05^4=3.067*10^{-7}\\;m^4, \\\\\\\\y=0.05/2=0.025\\;m$

$\\\\\\sigma =\\frac{125*0.025}{3.067*10^{-7}}=10.189\\;MPa$

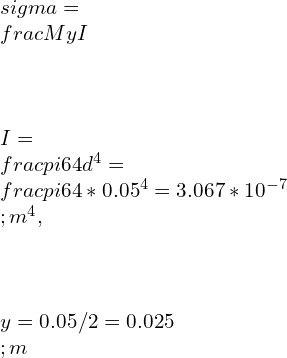
For a square specimen: wiith side =d = 50mm

$\\\\\\sigma =\\frac{My}{I}\\\\ \\\\\\sigma = \\frac{M(d/2)}{d^4/12} \\\\ \\\\\\sigma =\\frac{6M}{d^3} \\\\ \\\\\\sigma =\\frac{6*125}{0.05^3}\\\\ \\\\\\sigma =6 \\;MPa$

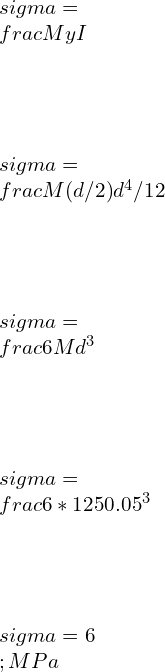
Some Important FAQs.

Q.1) What does high flexural strength mean?

Ans: A material is considered to possess high flexural strength, if it bears high amount of stress in flexing or bending condition without failure in a flexure test.

Q.2) Why is flexural strength higher than tensile strength?

Ans: During flexure test, the extreme fibers of the beam are experiencing maximum stress (top fiber experiences compressive stress and bottom fiber experiences tensile stress). If the extreme fibers are free from any defects, the flexural strength will depend upon the strength of the fibers which are yet to fail. However, when tensile load is applied to a material, all the fibers experience equal amount of stress and the material will fail upon the failure of the weakest fiber reaching its ultimate tensile strength value. Thus, In most cases flexural strength is higher than tensile strength of a material.

Q.3) What is the difference between flexure and bending?

Ans: In case of flexural bending, according to the theory of simple bending, the cross section of the plane remains plane before and after the bending. The bending moment generated acts along the entire span of the beam. no resultant force is acting perpendicular to cross section of the beam. thus, shear force along the beam is zero and any stress induced is purely due to bending effect only. In non-uniform bending, resultant force is acting perpendicular to cross section of the beam, and bending moment also varies along the span.

Q.4) Why is flexural strength important?

Ans: High flexural strength is critical for stress-bearing materials or components, when high stress is applied on the component or material. Flexural strength also assists in determining the indications for which type of material can be used for high pressure applications. High flexural strength of the material also affects the thickness of the component’s walls. A high-strength material permits low wall thickness. A material which provides high flexural strength and high fracture toughness allows very thin wall thickness to be manufactured and is therefore ideal for minimal invasive treatment options.

Q.5) find flexural strength from stress strain curve?

Ans: Flexural strength can be defined as the highest applied stress on the stress strain curve. The energy absorption by the material beforehand failure could be estimated by area under the stress-strain curve.

Q.6) Provide the maximum flexural strength of the M30 grade of concrete?

Ans: The compressive strength of M30 grade of concrete is 30 MPa. The relation between flexural strength and compressive strength can be given by:

$\\\\\\sigma_f =0.7\\sqrt{\\sigma_c}$

. Thus, the maximum flexural strength of the M30 grade of concrete is,

$\\\\\\sigma_f =0.7\\sqrt{30}=3.83\\;MPa$

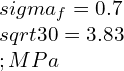
Q.7) Why is the maximum compressive strain in concrete in the flexural test 0.0035, not more or less, whereas the failure strain in concrete ranges from 0.003 to 0.005?

Ans: For theoretical calculation of maximum compressive strain in concrete in the flexural test, we consider all the assumptions of simple bending theory. During practical experimentation, various factors like defect in material, uneven cross section etc. affects the compressive strain in concrete in the flexural test. Thus, the maximum compressive strain in concrete in the flexural test 0.0035, not more or less, whereas the failure strain in concrete ranges from 0.003 to 0.005.

Q.8) If additional reinforcing bars are sited at compression side of a reinforced concrete beam. Is that enhance to the beam’s flexural strength?

Ans: Adding extra reinforcing bars provides additional strength to beam’s compressive strength, especially at the location at the positive moments occurs. The purpose of reinforcement bars is to prevent tensile failures like bending moment, since the concrete is weak in tensile loading. If the beam is high thickness along with reinforcement bars, the steel bars exclusively behave as tensile strength element while the concrete provides compression strength.

Q.9) What would happen to the flexural strength of a concrete beam if its dimensions are halved?

Ans: for a rectangular cross section beam,

In 3 – point bending setup, Flexural strength is given by

$\\\\\\sigma =\\frac{3WL}{2bd^2} \\\\\\\\\\sigma =\\frac{1.5WL}{bd^2}$

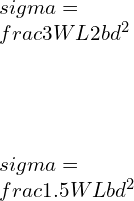
If the dimensions are halved
B = b/2, D = d/2

$\\\\\\sigma_1 =\\frac{3WL}{2BD^2} \\\\\\\\\\sigma_1 =\\frac{3WL}{2\\frac{b}{2}*\\frac{d^2}{4}}$

$\\\\\\sigma_1 =\\frac{12WL}{bd^2}$

$\\\\\\sigma_1 >\\sigma$

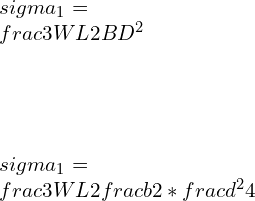
If the dimensions are halved, the flexural strength increased by 8 times for a rectangular cross-section material.

Q.10) What is modulus of rupture?

Ans: Flexural Modulus is a ratio of stress-induced during flexural bending to the strain during flexing deformation. It is the property or the ability of the material to resist bending.

To know about Simply Supported Beam (click here)and Cantilever beam (Click here .)

Hakimuddin Bawangaonwala

I am Hakimuddin Bawangaonwala , A Mechanical Design Engineer with Expertise in Mechanical Design and Development. I have Completed M. Tech in Design Engineering and has 2.5 years of Research Experience. Till now Published Two research papers on Hard Turning and Finite Element Analysis of Heat Treatment Fixtures. My Area of Interest is Machine Design, Strength of Material, Heat Transfer, Thermal Engineering etc. Proficient in CATIA and ANSYS Software for CAD and CAE. Apart from Research.

Content

Flexural strength

Flexural strength definition

Flexural strength formula | Flexural strength unit

Flexural strength test

Three-Point Bend test and Equations

Four-Point Bend test and Equations

Flexural strength vs Flexural Modulus

Flexural strength vs Tensile strength

Flexural strength of Concrete

Procedure for evaluating Flexure Strength of Concrete

Flexural strength of steel

Flexural strength of Aluminum

Flexural strength of Wood

Flexural strength of a Cylinder

Find the Flexural stress in the circular cylindrical beam with span of 10 m and diameter 50 mm. The beam is made of Aluminum. Compare the result with beam of square cross section with side = 50 mm. The total load applied is 70 N.

Some Important FAQs.

Q.1) What does high flexural strength mean?

Q.2) Why is flexural strength higher than tensile strength?

Q.3) What is the difference between flexure and bending?

Q.4) Why is flexural strength important?

Q.5) find flexural strength from stress strain curve?

Q.6) Provide the maximum flexural strength of the M30 grade of concrete?

Q.7) Why is the maximum compressive strain in concrete in the flexural test 0.0035, not more or less, whereas the failure strain in concrete ranges from 0.003 to 0.005?

Q.8) If additional reinforcing bars are sited at compression side of a reinforced concrete beam. Is that enhance to the beam’s flexural strength?

Q.9) What would happen to the flexural strength of a concrete beam if its dimensions are halved?

Q.10) What is modulus of rupture?

Leave a Comment