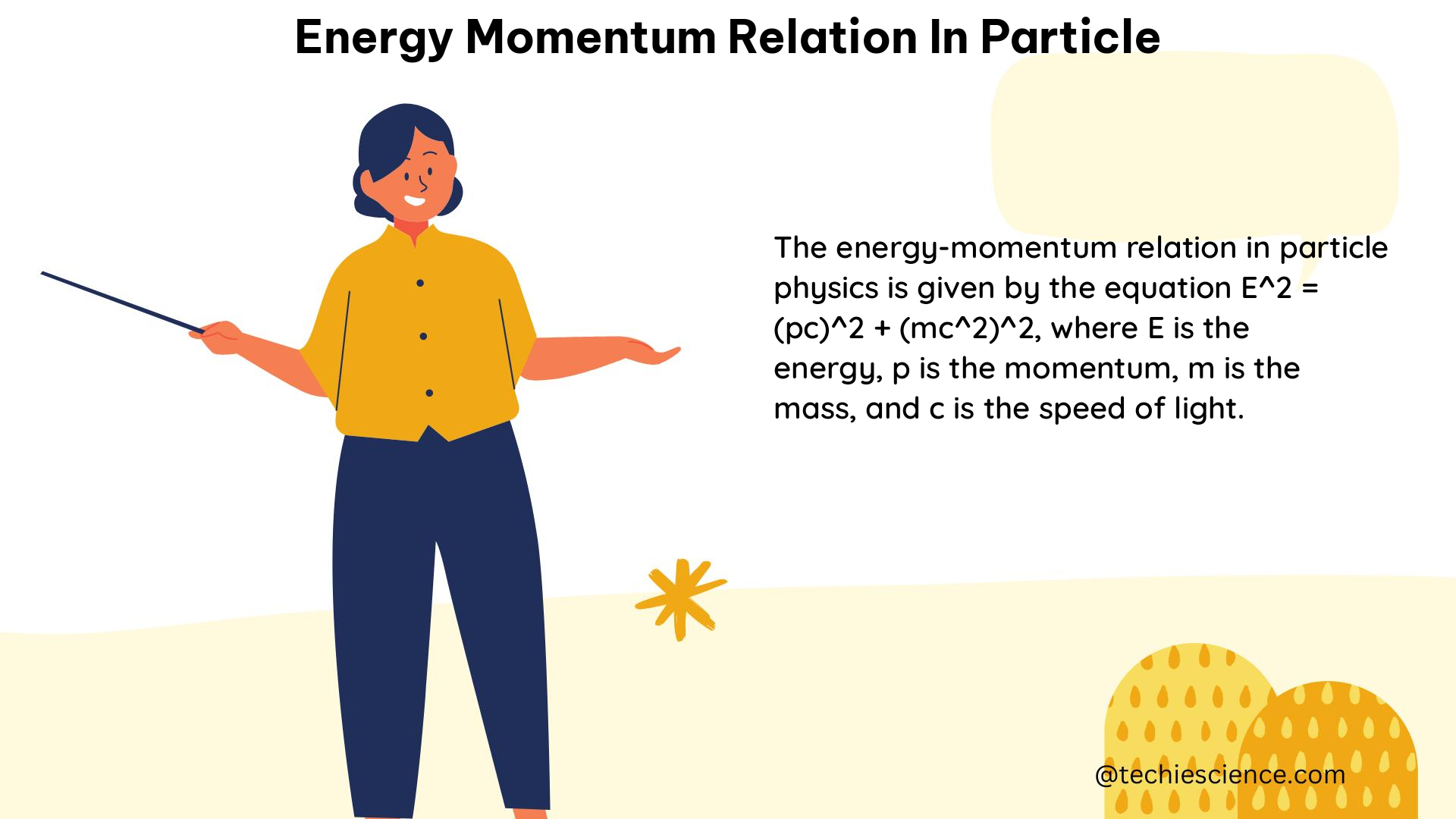
The Energy-Momentum Relation in Particle Physics: A Comprehensive Guide

The energy-momentum relation is a fundamental principle in particle physics that connects the energy (E), momentum (p), and mass (m) of a particle. This relation is expressed by the equation E^2 = (pc)^2 + (mc^2)^2, where c is the speed of light. This equation reveals that the total energy of a particle is the sum of its kinetic energy (the energy associated with its motion) and its rest energy (the energy associated with its mass).

Understanding the Energy-Momentum Relation

Relativistic Energy and Momentum

In the context of special relativity, the energy-momentum relation can be expressed as:

E^2 = (pc)^2 + (mc^2)^2

Where:
– E is the total energy of the particle
– p is the momentum of the particle
– m is the rest mass of the particle
– c is the speed of light

This equation shows that the total energy of a particle is the sum of its kinetic energy (pc) and its rest energy (mc^2).

Quantum Mechanical Perspective

In the context of quantum mechanics, the energy-momentum relation can be expressed in terms of wave quantities, such as the frequency (ω) and wavevector (k) of a matter wave. The energy-momentum relation can then be written as:

(ħω)^2 = (cħk)^2 + (m_0c^2)^2

Where:
– ħ is the reduced Planck constant
– ω is the frequency of the matter wave
– k is the wavevector of the matter wave
– m_0 is the rest mass of the particle

This equation shows that the frequency and wavevector of a matter wave are related to the mass and momentum of the corresponding particle.

Derivation of the Energy-Momentum Relation

The energy-momentum relation can be derived from the magnitude of the four-wavevector, which is a four-dimensional vector that includes the frequency and wavevector of a wave. This derivation is similar to the derivation of the four-momentum, which is a four-dimensional vector that includes the energy and momentum of a particle.

The four-wavevector is defined as:

k^μ = (ω/c, k)

Where:
– k^μ is the four-wavevector
– ω is the frequency of the wave
– k is the wavevector of the wave

The magnitude of the four-wavevector is given by:

k^μ k_μ = (ω/c)^2 – k^2 = (ħω)^2/c^2 – (ħk)^2 = (m_0c)^2

Rearranging this equation, we arrive at the energy-momentum relation:

(ħω)^2 = (cħk)^2 + (m_0c^2)^2

Implications of the Energy-Momentum Relation

Relativistic Dynamics

The energy-momentum relation has important implications for the behavior of particles in relativistic dynamics, which is the study of the motion of particles at high speeds.

High Velocity Limit

In the limit of high velocities, the energy-momentum relation approaches the equation E = pc, which is the exact relation between the energy and momentum of massless particles such as photons and neutrinos.

Low Velocity Limit

In the limit of low velocities, the energy-momentum relation reduces to the non-relativistic relation expressed by the equation E = mc^2 + p^2/2m.

Applications in Particle Physics

The energy-momentum relation is a fundamental concept in particle physics and has numerous applications, including:

1. Particle Accelerators: The energy-momentum relation is crucial in the design and operation of particle accelerators, where particles are accelerated to high energies to study their properties and interactions.

2. Particle Collisions: The energy-momentum relation is used to analyze the outcomes of particle collisions, where the conservation of energy and momentum can be used to infer the properties of the particles involved.

3. Particle Decay: The energy-momentum relation is used to study the decay of unstable particles, where the energy and momentum of the decay products can be used to infer the properties of the parent particle.

4. Particle Identification: The energy-momentum relation can be used to identify the type of particle based on its measured energy and momentum.

5. Relativistic Kinematics: The energy-momentum relation is used in the study of relativistic kinematics, which describes the motion of particles at high speeds.

Numerical Examples and Problems

Example 1: Relativistic Kinetic Energy

Calculate the relativistic kinetic energy of an electron with a momentum of 1 MeV/c. The rest mass of an electron is 0.511 MeV/c^2.

Given:
– Momentum (p) = 1 MeV/c
– Rest mass (m_0) = 0.511 MeV/c^2

Using the energy-momentum relation:
E^2 = (pc)^2 + (m_0c^2)^2
E = √[(pc)^2 + (m_0c^2)^2]
E = √[(1 MeV)^2 + (0.511 MeV)^2]
E = √(1 + 0.261) MeV
E = 1.128 MeV

Relativistic kinetic energy = E – m_0c^2 = 1.128 MeV – 0.511 MeV = 0.617 MeV

Problem 1: Relativistic Momentum

A proton has a kinetic energy of 10 GeV. Calculate its relativistic momentum.

Given:
– Kinetic energy (K) = 10 GeV

Using the energy-momentum relation:
E^2 = (pc)^2 + (m_0c^2)^2
(E – m_0c^2)^2 = (pc)^2
p^2 = (E – m_0c^2)^2/c^2
p = √[(E – m_0c^2)^2/c^2]

Where:
– E = K + m_0c^2 (total energy)
– m_0 = 0.938 GeV/c^2 (rest mass of proton)

Substituting the values:
E = 10 GeV + 0.938 GeV = 10.938 GeV
p = √[(10.938 GeV – 0.938 GeV)^2/c^2]
p = √[(10 GeV)^2/c^2]
p = 10 GeV/c

Therefore, the relativistic momentum of the proton is 10 GeV/c.

Conclusion

The energy-momentum relation is a fundamental principle in particle physics that connects the energy, momentum, and mass of a particle. It has important implications for the behavior of particles in relativistic dynamics and is a key concept in the study of particle physics. Understanding the energy-momentum relation is crucial for analyzing particle interactions, designing particle accelerators, and studying the properties of subatomic particles.

References

1. Energy-Momentum Relation – Wikipedia
2. Relativistic Energy and Momentum – Lumen Learning
3. Relativistic Momentum – Physics LibreTexts
4. Particle Physics – HyperPhysics
5. Relativistic Kinematics – University of Oregon