The term constant refers to steadiness. The object under motion whose acceleration is steady is called constant acceleration.
We know from the previous post that a uniform increase in velocity with a regular interval of time gives constant acceleration. Using an increase in velocity, we plot the constant acceleration on the graph, then if the velocity decreases steadily in the motion graph, can we plot a constant negative acceleration graph?
In a general sense, the motion of any object is positive. But while describing the motion, the entities like velocity and acceleration can be negative. Since the integral value of acceleration gives the velocity, it does not mean that negative velocity gives negative acceleration.
Now let us learn what is constant negative acceleration means and how to plot a constant negative acceleration graph in the following section.
What is constant negative acceleration graph?
Suppose a particle is moving at a certain speed and suddenly the speed of the particle is decreasing; it may be due to friction or due to loss of energy. Then if we plot the decreasing speed on the graph, we get a negative slope.
When the particle’s velocity decreases consistently with time, there will be a decrease in the slope of the particle’s motion. The acceleration of the particle will be unvarying, and it is acted in the direction opposite to the direction of motion; such acceleration can be interpreted on a graph called a constant negative acceleration graph.

For example, a person is driving a car that has a certain velocity. The driver has to slow down the speed of the car due to a traffic signal. The velocity is decreasing linearly, and hence the acceleration will act in the direction opposite to the velocity. Hence the car has attained negative acceleration. Since the velocity is decreasing at a uniform rate, the plot of the motion of the car has a constant negative acceleration graph.
Constant negative acceleration position time graph
The constant negative acceleration can be plotted using the position-time graph. In the position-time graph, the acceleration will be constant only when the path traced by the particle on the x-t graph is a parabolic curve.
The position-time graph represents the distance traveled by the particle in the given time; thus, its slope gives the change in velocity. The time is always zero or non-negative numbers; thus, we always take the time in the positive axis. We can say that if the slope of the x-t graph decreases constantly, we can achieve negative acceleration graph.
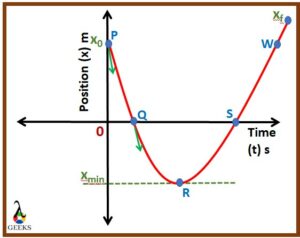
From the above x-t graph, we can say that,
- At point P: the point p is the initial position of the particle at time t=0. This is the position from where the particle has begun its motion. The velocity at this position is the initial velocity of the particle (v0).
- Curve PR: between the points P and R, the particle is traveling towards the negative x-direction. The slope is decreasing between the points P and Q. The slope of the curve keeps on decreasing as the particle moves from P to R. Thus, there is a constant variation in the velocity, and we get constant negative acceleration between the curve P and R.
- Points Q and S: The parabolic curve traced by the particle intersects the x-axis at points Q and S. The time corresponding to points Q and S give the real roots of the quadratic equation.
- At Point R: The slope of the curve at point R is zero, and at this position, the particle will be at rest. The particle can change its direction only once during the motion; the point Q is the position where the particle can reverse its motion under constant acceleration. So at point R, the particle changes its sign.
- Curve RW: The curve traced by the particle now has increased its slope, and thus the magnitude of the velocity increases, and now the particle attain constant positive acceleration.
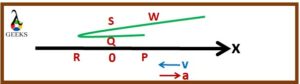
- Point W and Z: At point W, the particle is in a position equal to its initial position and has the same initial velocity. At point Z, which is the final position of the particle thus the motion is retarded. The constant negative acceleration can be given by free body diagram as given below.
The general expression for distance traveled by a particle from the kinematic equation is given by
The above equation is similar to the quadratic equation,
Ax2+Bx+c=0
Comparing the above two equations, the determinant of the quadratic equation is given by
D= B2 – 4AC
D = v02 – 2ax0
When the particle is at x=0, the quadratic equation has real non zero roots; thus the determinant can be rewritten as
D = v02 – 2ax0 ≥ 0
v02 ≥ 2ax0
The value of x is given by the quadratic equation is;
In the case of constant negative acceleration, the coefficient of t2 would be negative as the slope of the parabolic curve is decreasing, so the maximum value of x is given by
From the above explanation, we can say that the acceleration is negative and constant as the acceleration is opposite to the origin that we have considered as the reference point and the change in velocity is constant as we consider the uniform motion.
So it is clear that the acceleration is negative or positive based on the reference point.
Constant negative acceleration velocity time graph
If suddenly the motion of the particle decreases steadily with time, the slope of the velocity-time graph decreases. The decrease in the slope of the graph gives the negative acceleration on the graph.
Suppose the slope of the v-t graph increases, the acceleration will be more significant. But the slope is decreasing at a steady rate; hence the particle is decelerating.
The graph of velocity vs. time is given below:

From the v-t graph, we can say that,
- v0 is the initial velocity of the particle, from where the velocity is decreasing with time.
- The velocity of the particle intersects the origin in the X-axis at point P, where the particle tends to reverse its direction of motion.
- v is the final velocity of the particle achieved by inverting its sign. The velocity now is the negative velocity with decreasing slope.
The slope of steady decrease of velocity with time is given by,
From the graph, the change in the velocity is given by
∆v = v – v0
We have the final velocity is in the negative axis, hence
Thus we get the slope as
The acceleration obtained by the graph has a negative sign, which means the particle is decelerating with a constant decrease in velocity. Thus we get a constant negative acceleration graph by plotting the v-t graph.
For example, consider a rider riding a bike on a dirt track. Initially, he was riding the bike with the velocity of v0, suddenly he encountered an obstacle, and his speed was gradually decreasing at a constant rate with time, and after crossing the obstacle, his speed remained constant for some time, and it slowly increased to reach his initial velocity. The interpretation of the Velocity-time graph for the bike is given below.

- At point P: the time t=0, the velocity of the bike is beginning to decrease with time at a steady rate.
- Between P and Q: the velocity of the bike decreases between the point P and Q, thus the slope becomes negative between those points. At point Q, the bike attains the velocity v, which is the minimum velocity of the bike during its motion. Hence the acceleration at this path is given by
The magnitude of the slope gives the acceleration. Since the slope is decreasing and has attained the negative value even though the velocity is still in the positive axis, thus constant negative acceleration graph is plotted between the points P and Q.
- Between Q and R: The velocity of the bike is constant along with the path Q and R; thus, there is no acceleration of the bike along the path Q and R. ie., a=0.
- Between R and S: The velocity increases along the path R and S Thus, reaching the bike’s initial velocity at point S., the velocity at point S is now equal to the velocity at point P.
- At point W: the velocity of the bike is vf, the final velocity that bike has acquired; at this point, the bike has stopped.
Thus to achieve a constant negative acceleration graph using the velocity-time, the particle has to lose its velocity, and the slope has to be decreased.
Also Read:
- How to find acceleration with mass and force and friction
- How to find acceleration with time and displacement
- How to find max acceleration in simple harmonic motion
- How to find acceleration with kinematic equations
- Centripetal acceleration and centrifugal acceleration
- How to find instantaneous acceleration
- Angular acceleration and centripetal acceleration
- How to find gravitational acceleration without mass
- How to find acceleration of gravity
- How to calculate acceleration with force and mass
I am Keerthi K Murthy, I have completed post graduation in Physics, with the specialization in the field of solid state physics. I have always consider physics as a fundamental subject which is connected to our daily life. Being a science student I enjoy exploring new things in physics. As a writer my goal is to reach the readers with the simplified manner through my articles.