Centripetal acceleration and acceleration are two concepts that are often confused but have distinct meanings. Acceleration is a fundamental concept in physics that refers to the rate of change of velocity with respect to time. It is a vector quantity, meaning it has both magnitude and direction. On the other hand, centripetal acceleration is a specific type of acceleration that occurs when an object moves in a circular path. It is always directed towards the center of the circle and is responsible for keeping the object moving in a curved trajectory. While both centripetal acceleration and acceleration involve changes in velocity, they differ in terms of their direction and the forces involved. Understanding the differences between these two concepts is crucial for grasping the dynamics of circular motion and its applications in various fields such as mechanics, astronomy, and engineering.
Key Takeaways
| Centripetal Acceleration | Acceleration |
|---|---|
| Always directed towards the center of the circle | Can be directed in any direction |
| Causes an object to move in a circular path | Can cause an object to change speed or direction |
| Depends on the radius and speed of the object | Depends on the net force acting on the object |
| Measured in meters per second squared (m/s²) | Also measured in meters per second squared (m/s²) |
| Formula: (a_c = frac{v^2}{r}) | Formula: (a = frac{Delta v}{Delta t}) |
Normal Acceleration vs Centripetal Acceleration
Explanation of normal acceleration and its characteristics
When we think about acceleration, we often picture a car speeding up or slowing down. However, acceleration is not just about changes in speed. It also involves changes in direction. This is where normal acceleration comes into play.
Normal acceleration refers to the rate at which an object changes its direction while moving along a curved path. It is called “normal” because it is perpendicular to the object’s velocity vector at any given point. In simpler terms, normal acceleration is the force that keeps an object moving in a curved path.
To better understand normal acceleration, let’s consider the example of a car driving along a circular track. As the car moves around the track, it experiences a force towards the center of the circle, known as the centripetal force. This force is responsible for the car’s circular motion. The normal acceleration of the car is directly proportional to the centripetal force and inversely proportional to the mass of the car.
Comparison with centripetal acceleration and their differences
Now that we have a grasp of normal acceleration, let’s compare it to centripetal acceleration and explore their differences.
Centripetal acceleration, on the other hand, is the acceleration experienced by an object moving in a circular path. It is also directed towards the center of the circle, just like the centripetal force. However, unlike normal acceleration, centripetal acceleration is not concerned with changes in direction. Instead, it focuses solely on changes in speed.
To put it simply, centripetal acceleration is the acceleration that keeps an object moving in a circular path at a constant speed. It is responsible for maintaining the object’s velocity vector tangent to the circle.
One key difference between normal acceleration and centripetal acceleration is their relationship to velocity. Normal acceleration is perpendicular to the velocity vector, while centripetal acceleration is tangent to the velocity vector. Another difference lies in their formulas. Normal acceleration can be calculated using the equation a_normal = v^2/r, where v is the velocity of the object and r is the radius of the circular path. On the other hand, centripetal acceleration can be calculated using the equation a_centripetal = v^2/r.
To summarize, normal acceleration is the rate at which an object changes its direction while moving along a curved path, while centripetal acceleration is the acceleration experienced by an object moving in a circular path. Normal acceleration is perpendicular to the velocity vector, while centripetal acceleration is tangent to the velocity vector.
Relationship between Centripetal Acceleration and Angular Velocity
Centripetal acceleration and angular velocity are two fundamental concepts in the study of circular motion. Understanding the connection between these two quantities is crucial for comprehending the dynamics of objects moving in circular paths. In this section, we will explore the relationship between centripetal acceleration and angular velocity, as well as how changes in angular velocity affect centripetal acceleration.
Understanding the Connection between Centripetal Acceleration and Angular Velocity
Centripetal acceleration is the acceleration experienced by an object moving in a circular path. It is always directed towards the center of the circle and is responsible for keeping the object on its curved trajectory. On the other hand, angular velocity refers to the rate at which an object rotates around a fixed axis. It is a vector quantity and is measured in radians per second.
To understand the connection between centripetal acceleration and angular velocity, let’s consider a simple example. Imagine a car moving along a circular track. As the car accelerates, it experiences a centripetal force that keeps it on the track. This force is provided by the friction between the car’s tires and the road surface. The magnitude of the centripetal force depends on the mass of the car, the radius of the circular track, and the car’s speed.
Now, let’s relate this to angular velocity. The angular velocity of the car is determined by how quickly it rotates around the center of the circular track. If the car completes one full revolution in a given time, its angular velocity is higher compared to a car that takes more time to complete the same revolution. In other words, the faster the car rotates, the higher its angular velocity.
Explanation of How Changes in Angular Velocity Affect Centripetal Acceleration
Now that we understand the connection between centripetal acceleration and angular velocity, let’s explore how changes in angular velocity affect centripetal acceleration.
When the angular velocity of an object in circular motion changes, its centripetal acceleration also changes. This can be observed by considering the centripetal acceleration formula, which is given by:
![]()
where ( a_c ) represents the centripetal acceleration, ( v ) is the linear velocity of the object, and ( r ) is the radius of the circular path.
If the angular velocity of the object increases, its linear velocity also increases. As a result, the centripetal acceleration increases because the object is moving faster along the circular path. Conversely, if the angular velocity decreases, the linear velocity decreases, leading to a decrease in centripetal acceleration.
It’s important to note that centripetal acceleration is always perpendicular to the linear velocity of the object. This means that even if the object is moving at a constant speed, its centripetal acceleration can change if the direction of its linear velocity changes. This is because the centripetal acceleration is determined by the change in direction of the object’s velocity, rather than its speed.
In summary, centripetal acceleration and angular velocity are closely related in circular motion. Changes in angular velocity directly affect the centripetal acceleration experienced by an object. By understanding this relationship, we can gain insights into the dynamics of objects moving in circular paths and how their accelerations change with varying angular velocities.
Direction of Centripetal Acceleration
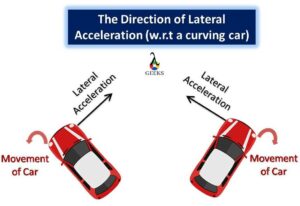
Centripetal acceleration is a concept that describes the acceleration experienced by an object moving in a circular path. In this section, we will explore the direction in which centripetal acceleration acts and discuss the factors that determine its direction.
Explanation of the direction in which centripetal acceleration acts
When an object moves in a circular path, it experiences a force called the centripetal force, which is directed towards the center of the circle. This force is responsible for causing the object to continuously change its direction, even though its speed may remain constant.
The direction of centripetal acceleration is always towards the center of the circle. This means that the object is accelerating towards the center of the circle, even though its speed may not be changing. It is important to note that centripetal acceleration is always perpendicular to the velocity of the object at any given point on its path.
To better understand this concept, let’s consider the example of a car moving along a curved road. As the car takes a turn, it experiences a centripetal force that acts towards the center of the curve. This force causes the car to accelerate towards the center of the curve, allowing it to maintain its circular path.
Discussion of the factors determining the direction of centripetal acceleration
The direction of centripetal acceleration is determined by two main factors: the direction of the velocity vector and the curvature of the circular path.
-
Direction of the velocity vector: The velocity vector of an object moving in a circular path is always tangent to the circle at any given point. The centripetal acceleration vector, on the other hand, is directed towards the center of the circle. Therefore, the direction of centripetal acceleration is always perpendicular to the velocity vector.
-
Curvature of the circular path: The curvature of the circular path determines the magnitude of the centripetal acceleration. If the curvature of the path increases, the centripetal acceleration also increases. However, the direction of the centripetal acceleration remains the same, always pointing towards the center of the circle.
In summary, the direction of centripetal acceleration is always towards the center of the circle, perpendicular to the velocity vector of the object. The magnitude of the centripetal acceleration depends on the curvature of the circular path. Understanding the direction of centripetal acceleration is crucial in analyzing circular motion and its effects on objects moving in curved paths.
Centripetal Acceleration vs Radial Acceleration
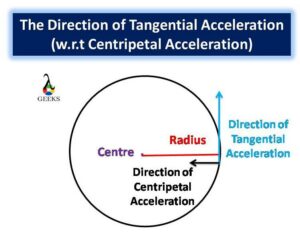
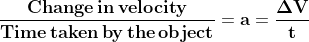
Differentiating between centripetal acceleration and radial acceleration
Centripetal acceleration and radial acceleration are two terms often used in the context of circular motion. While they may sound similar, they have distinct meanings and implications. Let’s explore the differences between these two types of acceleration.
Centripetal acceleration refers to the acceleration experienced by an object moving in a circular path. It is always directed towards the center of the circle and is responsible for keeping the object in its curved trajectory. This acceleration is caused by a centripetal force acting on the object, which is necessary to counteract the natural tendency of the object to move in a straight line.
On the other hand, radial acceleration refers to the acceleration component that is directed along the radius of the circular path. It is perpendicular to the tangential velocity of the object and is responsible for changing the direction of the object’s velocity. Unlike centripetal acceleration, radial acceleration does not necessarily point towards the center of the circle. Instead, it can be directed towards or away from the center, depending on the specific motion of the object.
Explanation of their similarities and differences
While centripetal acceleration and radial acceleration are distinct concepts, they are related and can be thought of as different aspects of the same phenomenon. Here are some key similarities and differences between them:
-
Direction: Centripetal acceleration always points towards the center of the circle, while radial acceleration can be directed towards or away from the center.
-
Magnitude: The magnitude of centripetal acceleration is determined by the speed of the object and the radius of the circular path it follows. In contrast, the magnitude of radial acceleration depends on the rate at which the object’s direction changes.
-
Relationship to velocity: Centripetal acceleration is always perpendicular to the object’s velocity, while radial acceleration is perpendicular to the tangential component of the object’s velocity.
-
Relationship to centripetal force: Centripetal acceleration is directly related to the centripetal force acting on the object. The centripetal force is responsible for providing the necessary inward acceleration to keep the object in its circular path. Radial acceleration, on the other hand, is not directly related to any specific force but is a result of the object’s changing direction.
To summarize, centripetal acceleration and radial acceleration are two distinct components of the overall acceleration experienced by an object in circular motion. Centripetal acceleration is always directed towards the center of the circle and is responsible for maintaining the object’s curved path, while radial acceleration is perpendicular to the tangential velocity and is responsible for changing the object’s direction. Understanding these concepts is crucial for comprehending the dynamics of circular motion.
Centripetal Acceleration vs Gravitational Acceleration
Comparison of Centripetal Acceleration and Gravitational Acceleration
When it comes to understanding the motion of objects, two important concepts to consider are centripetal acceleration and gravitational acceleration. While they both involve the idea of acceleration, they have distinct characteristics and applications.
Centripetal acceleration refers to the acceleration experienced by an object moving in a circular path. It is always directed towards the center of the circle and is responsible for keeping the object in its circular trajectory. On the other hand, gravitational acceleration is the acceleration experienced by an object due to the force of gravity.
One key difference between centripetal acceleration and gravitational acceleration is the source of the force that causes the acceleration. Centripetal acceleration is caused by a centripetal force, which is directed towards the center of the circular path. This force can be provided by various factors, such as tension in a string, friction, or even the normal force. Gravitational acceleration, on the other hand, is caused by the gravitational force exerted by a massive object, such as the Earth.
Another difference lies in the direction of the acceleration. Centripetal acceleration is always directed towards the center of the circle, perpendicular to the velocity of the object. This means that it changes the direction of the object’s velocity but not its magnitude. Gravitational acceleration, on the other hand, is always directed towards the center of the massive object, such as the Earth. It acts vertically downwards and can change both the direction and magnitude of an object’s velocity.
Discussion of their Distinct Characteristics and Applications
Centripetal acceleration and gravitational acceleration have distinct characteristics that make them applicable in different scenarios. Let’s take a closer look at their unique features and applications.
Centripetal Acceleration
Centripetal acceleration is a crucial concept in circular motion and is used to describe the acceleration of objects moving in a circular path. It is responsible for keeping objects in orbit, such as satellites around the Earth or planets around the Sun. Without centripetal acceleration, these objects would move off in a straight line due to their inertia.
The formula for centripetal acceleration depends on the object’s velocity and the radius of the circular path. It can be derived from the centripetal force acting on the object. By using the equation a = v^2/r, where a represents centripetal acceleration, v is the velocity, and r is the radius, we can calculate the magnitude of the acceleration.
Gravitational Acceleration
Gravitational acceleration, also known as the acceleration due to gravity, is a force that attracts objects towards the center of the Earth. It is responsible for keeping us grounded and objects from floating away into space. The acceleration due to gravity on Earth is approximately 9.8 m/s^2.
Gravitational acceleration plays a significant role in various fields, such as physics, engineering, and astronomy. It is used to calculate the weight of objects, determine the motion of celestial bodies, and understand the behavior of free-falling objects. The acceleration due to gravity can also vary depending on the location, such as on other planets or in space.
In conclusion, while both centripetal acceleration and gravitational acceleration involve the concept of acceleration, they have distinct characteristics and applications. Centripetal acceleration is associated with circular motion and is directed towards the center of the circle, while gravitational acceleration is caused by the force of gravity and acts vertically downwards. Understanding these concepts is essential in comprehending the motion of objects in various scenarios, from satellites orbiting the Earth to objects falling towards the ground.
Working of Centripetal Acceleration
Centripetal acceleration is a fundamental concept in physics that helps us understand how objects move in circular paths. In this section, we will explore how centripetal acceleration operates on objects in circular motion and discuss the forces involved in generating this acceleration.
Explanation of how centripetal acceleration operates on objects in circular motion
When an object moves in a circular path, it experiences a force directed towards the center of the circle. This force is called the centripetal force. It is responsible for keeping the object in its circular path and preventing it from moving in a straight line.
To understand how centripetal acceleration operates on objects in circular motion, let’s consider the example of a car taking a turn on a curved road. As the car turns, it experiences a force towards the center of the curve. This force is provided by the friction between the car’s tires and the road surface. The centripetal force acts as the inward force that keeps the car moving in a curved path.
The centripetal acceleration of an object is the rate at which its velocity changes as it moves in a circular path. It is always directed towards the center of the circle and is perpendicular to the object’s velocity vector at any given point. The magnitude of centripetal acceleration can be calculated using the formula:
a = v^2 / r
where “a” is the centripetal acceleration, “v” is the velocity of the object, and “r” is the radius of the circular path.
Discussion of the forces involved in generating centripetal acceleration
In circular motion, there are two main forces involved in generating centripetal acceleration: the centripetal force and the normal force.
The centripetal force, as mentioned earlier, is responsible for keeping the object in its circular path. It acts towards the center of the circle and is equal to the product of the object’s mass and centripetal acceleration. In the case of the car turning on a curved road, the centripetal force is provided by the friction between the tires and the road surface.
The normal force is the force exerted by a surface to support the weight of an object resting on it. In the context of circular motion, the normal force acts perpendicular to the surface and is directed towards the center of the circle. It helps balance the inward centripetal force and prevents the object from sinking into the surface.
In summary, centripetal acceleration operates on objects in circular motion by causing a change in their velocity, keeping them in their circular path. This acceleration is generated by the centripetal force, which acts towards the center of the circle, and is balanced by the normal force. Understanding the working of centripetal acceleration is crucial in various fields, such as physics, engineering, and even everyday activities like driving.
Importance of Centripetal Acceleration
Centripetal acceleration plays a crucial role in various contexts, from understanding circular motion to maintaining stability. Let’s delve into the significance of centripetal acceleration and explore its role in different scenarios.
Understanding the Significance of Centripetal Acceleration in Various Contexts
Centripetal acceleration is a concept that helps us comprehend the motion of objects moving in a circular path. It is the acceleration directed towards the center of the circle, enabling an object to continuously change its direction without altering its speed. This concept finds applications in numerous fields, including physics, engineering, and everyday life.
In physics, centripetal acceleration is vital for understanding rotational motion. It allows us to analyze the forces acting on an object moving in a circular path. By considering the centripetal acceleration, we can determine the magnitude and direction of the force required to keep the object on its circular trajectory.
In engineering, centripetal acceleration is crucial for designing and maintaining stable systems. For example, when designing a roller coaster, engineers must consider the centripetal acceleration to ensure the safety and comfort of the riders. By calculating the required centripetal acceleration, they can determine the appropriate banking angle of the track and the necessary frictional force to prevent any mishaps.
Discussion of Its Role in Maintaining Circular Motion and Stability
Centripetal acceleration is essential for maintaining circular motion and stability. Without it, objects moving in a circular path would veer off tangentially, resulting in a loss of control and stability.
When an object moves in a circular path, it experiences a continuous change in direction. This change in direction requires a force directed towards the center of the circle, known as the centripetal force. The centripetal force is responsible for providing the necessary centripetal acceleration to keep the object on its circular path.
In the absence of centripetal acceleration, an object would continue moving in a straight line due to its inertia. This is known as tangential acceleration, which is the acceleration in the direction tangent to the circular path. However, without the centripetal acceleration, the object would no longer follow a circular trajectory and would instead move in a straight line.
Centripetal acceleration is also closely related to stability. In systems where stability is crucial, such as vehicles taking sharp turns, the centripetal acceleration must be carefully considered. For example, when driving a car around a curve, the centripetal acceleration is responsible for keeping the car on the road and preventing it from skidding off. By adjusting the speed and the centripetal force, drivers can maintain control and ensure a safe turn.
In conclusion, centripetal acceleration plays a vital role in various contexts, allowing us to understand circular motion and maintain stability. Its significance in physics and engineering cannot be overstated, as it enables us to analyze forces, design safe systems, and ensure controlled motion. By grasping the concept of centripetal acceleration, we gain a deeper understanding of the mechanics behind circular motion and its applications in our daily lives.
Occurrence of Centripetal Acceleration in Objects
Centripetal acceleration is a fundamental concept in physics that describes the acceleration experienced by an object moving in a circular path. It is important to understand the conditions under which centripetal acceleration occurs and the various objects and scenarios where it is observed.
Explanation of the conditions under which centripetal acceleration occurs
Centripetal acceleration occurs when an object is moving in a circular path and experiences a force directed towards the center of the circle. This force is known as the centripetal force. According to Newton’s second law of motion, the acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass. In the case of centripetal acceleration, the net force acting on the object is the centripetal force.
To maintain circular motion, an object must constantly change its direction, which requires a force to act towards the center of the circle. This force is responsible for keeping the object in its circular path. Without this force, the object would move in a straight line tangent to the circle.
Examples of objects and scenarios where centripetal acceleration is observed
Centripetal acceleration can be observed in various objects and scenarios in our daily lives. Here are a few examples:
-
Car turning a corner: When a car turns a corner, it experiences centripetal acceleration. As the car takes the curved path, the tires exert a centripetal force on the car, keeping it in the circular motion. This force allows the car to change its direction without sliding off the road.
-
Satellite orbiting the Earth: Satellites in orbit around the Earth experience centripetal acceleration. The gravitational force between the satellite and the Earth acts as the centripetal force, keeping the satellite in its circular orbit. This allows the satellite to maintain a constant distance from the Earth while moving at a high speed.
-
Child on a merry-go-round: When a child sits on a merry-go-round and it starts spinning, the child experiences centripetal acceleration. The force of friction between the child and the merry-go-round provides the centripetal force, keeping the child in circular motion. This force prevents the child from flying off the merry-go-round.
-
Cyclist going around a curve: When a cyclist goes around a curve, they experience centripetal acceleration. The friction between the tires and the road provides the necessary centripetal force, allowing the cyclist to navigate the curve without skidding.
In all these examples, centripetal acceleration is observed because there is a force acting towards the center of the circular path, allowing the objects to maintain their curved motion.
In conclusion, centripetal acceleration occurs when an object moves in a circular path and experiences a force directed towards the center of the circle. It can be observed in various objects and scenarios, such as cars turning corners, satellites orbiting the Earth, children on merry-go-rounds, and cyclists going around curves. Understanding centripetal acceleration is essential for comprehending the dynamics of circular motion in the world around us.
Location of Maximum Centripetal Acceleration
Centripetal acceleration refers to the acceleration experienced by an object moving in a circular path. In this section, we will explore the identification of the points where centripetal acceleration is the greatest and the factors that influence its magnitude.
Identification of the Points where Centripetal Acceleration is the Greatest
When an object moves in a circular path, there are specific points where the centripetal acceleration is the greatest. These points are crucial to understanding the dynamics of circular motion.
-
Outer Edge of the Circular Path: At the outer edge of the circular path, the centripetal acceleration is at its maximum. This is because the object is farther away from the center of the circle, resulting in a larger radius. According to the centripetal acceleration formula, which states that acceleration is directly proportional to the square of the velocity divided by the radius, the larger radius leads to a greater centripetal acceleration.
-
Inner Edge of the Circular Path: Conversely, at the inner edge of the circular path, the centripetal acceleration is the smallest. This is because the object is closer to the center of the circle, resulting in a smaller radius. As per the centripetal acceleration formula, the smaller radius leads to a smaller centripetal acceleration.
-
Midpoint of the Circular Path: At the midpoint of the circular path, the centripetal acceleration is intermediate between the maximum and minimum values. This is because the midpoint represents an average distance from the center of the circle, resulting in an average radius. Consequently, the centripetal acceleration at this point is neither the greatest nor the smallest.
Factors Influencing the Magnitude of Centripetal Acceleration
Several factors influence the magnitude of centripetal acceleration. Let’s take a closer look at these factors:
-
Velocity of the Object: The velocity of the object moving in a circular path has a direct impact on the magnitude of centripetal acceleration. According to the centripetal acceleration formula, acceleration is directly proportional to the square of the velocity. Therefore, the higher the velocity, the greater the centripetal acceleration.
-
Radius of the Circular Path: The radius of the circular path also plays a significant role in determining the magnitude of centripetal acceleration. As mentioned earlier, the centripetal acceleration is inversely proportional to the radius. Thus, a larger radius results in a smaller centripetal acceleration, while a smaller radius leads to a greater centripetal acceleration.
-
Mass of the Object: The mass of the object moving in a circular path affects the magnitude of centripetal acceleration. However, it is important to note that the mass does not directly influence the centripetal acceleration. Instead, it affects the force required to maintain the circular motion. According to Newton’s second law of motion, the force is equal to the mass multiplied by the centripetal acceleration. Therefore, a greater mass requires a larger force, which in turn leads to a greater centripetal acceleration.
-
Applied Force: The force applied to the object also affects the magnitude of centripetal acceleration. If an external force is applied in the direction of the circular path, it can increase the centripetal acceleration. On the other hand, if the applied force opposes the circular motion, it can decrease the centripetal acceleration.
In conclusion, the location of maximum centripetal acceleration can be identified at the outer edge of the circular path, while the inner edge represents the minimum value. The magnitude of centripetal acceleration is influenced by factors such as the velocity of the object, the radius of the circular path, the mass of the object, and the applied force. Understanding these factors is essential for comprehending the dynamics of circular motion and its associated acceleration.
Angular Acceleration vs Centripetal Acceleration vs Tangential Acceleration
When discussing the concept of acceleration, it is important to understand the distinctions between angular acceleration, centripetal acceleration, and tangential acceleration. Each of these types of acceleration plays a unique role in various physical phenomena. Let’s explore the differences and relationships between them.
Differentiating between Angular Acceleration, Centripetal Acceleration, and Tangential Acceleration
Angular Acceleration refers to the rate at which an object’s angular velocity changes over time. It is a measure of how quickly an object’s rotational motion is changing. Angular acceleration is denoted by the symbol “α” and is expressed in units of radians per second squared (rad/s²). It is calculated using the formula:
α = Δω / Δt
where Δω represents the change in angular velocity and Δt represents the change in time.
Centripetal Acceleration is the acceleration experienced by an object moving in a circular path. It is always directed towards the center of the circle and is responsible for keeping the object in its circular trajectory. Centripetal acceleration is given by the formula:
ac = v² / r
where “v” represents the velocity of the object and “r” represents the radius of the circular path.
Tangential Acceleration is the component of acceleration that is tangent to the circular path. It is responsible for changing the magnitude of an object’s velocity as it moves along the circular path. Tangential acceleration can be calculated using the formula:
at = α * r
where “α” represents the angular acceleration and “r” represents the radius of the circular path.
Explanation of their Individual Characteristics and Relationships
Angular acceleration, centripetal acceleration, and tangential acceleration are interconnected and play crucial roles in circular motion.
-
Angular acceleration determines how quickly an object’s rotational motion changes. It is influenced by the torque acting on the object and can be positive or negative, depending on the direction of the change in angular velocity.
-
Centripetal acceleration is responsible for keeping an object moving in a circular path. It is always directed towards the center of the circle and is proportional to the square of the object’s velocity. As the velocity increases, so does the centripetal acceleration.
-
Tangential acceleration affects the magnitude of an object’s velocity as it moves along the circular path. It is directly proportional to the angular acceleration and the radius of the circular path. If the angular acceleration increases or the radius decreases, the tangential acceleration will also increase.
To better understand the relationships between these types of acceleration, let’s consider an example. Imagine a car moving along a curved road. The car‘s wheels are rotating, resulting in angular acceleration. This angular acceleration leads to tangential acceleration, which changes the car’s linear velocity as it moves along the curved path. At the same time, the car experiences centripetal acceleration, which keeps it on the road and prevents it from veering off in a straight line.
In summary, angular acceleration, centripetal acceleration, and tangential acceleration are distinct but interconnected concepts that play vital roles in circular motion. Understanding these concepts allows us to comprehend the forces and motions involved in various phenomena, from the rotation of objects to the movement of vehicles along curved paths.
Centripetal vs Centrifugal
Comparison of centripetal acceleration and centrifugal acceleration
Centripetal acceleration and centrifugal acceleration are two terms often used when discussing circular motion. While they may sound similar, they actually represent different aspects of an object’s motion. Let’s take a closer look at each of them and understand their differences.
Centripetal acceleration refers to the acceleration experienced by an object moving in a circular path. It is always directed towards the center of the circle and is responsible for keeping the object in its circular path. On the other hand, centrifugal acceleration is a term commonly used to describe the apparent outward force experienced by an object in circular motion. It is important to note that centrifugal acceleration is not a real force but rather a perceived force due to the inertia of the object.
To better understand the distinction between centripetal and centrifugal acceleration, let’s consider an example. Imagine you are driving a car around a curved road. As you steer the car, it follows a circular path. The centripetal acceleration is the force that keeps the car moving in the curved path, pulling it towards the center of the circle. This force is provided by the friction between the tires and the road surface. On the other hand, the centrifugal acceleration is the apparent outward force that you feel as the car turns. This force is a result of your body’s inertia, which tends to keep you moving in a straight line.
Understanding their opposing directions and relationship
One important aspect to note is that centripetal and centrifugal acceleration have opposing directions. Centripetal acceleration is directed towards the center of the circle, while centrifugal acceleration appears to be directed away from the center. This apparent outward force is a result of the inertia of the object trying to maintain its straight-line motion.
It is important to understand that centripetal and centrifugal acceleration are not independent of each other. They are two sides of the same coin, representing different perspectives of the same motion. Centripetal acceleration is the force that keeps an object in circular motion, while centrifugal acceleration is the apparent outward force experienced by the object due to its inertia.
To summarize, centripetal acceleration is the force that keeps an object moving in a circular path, always directed towards the center of the circle. On the other hand, centrifugal acceleration is the apparent outward force experienced by the object due to its inertia. While they may seem like opposing forces, they are actually two different perspectives of the same motion.
In the next section, we will delve deeper into the formulas and equations used to calculate centripetal acceleration and further explore their relationship.
Difference between Centripetal Acceleration and Centripetal Force
Explanation of the distinction between centripetal acceleration and centripetal force
When it comes to circular motion, two important concepts to understand are centripetal acceleration and centripetal force. While they may sound similar, they actually refer to different aspects of an object’s motion.
Centripetal acceleration is the acceleration experienced by an object moving in a circular path. It is always directed towards the center of the circle and is responsible for continuously changing the direction of the object’s velocity. In simpler terms, it is the acceleration that keeps an object moving in a circular path.
On the other hand, centripetal force is the force that acts on an object moving in a circular path, pulling it towards the center of the circle. It is the force that is required to maintain the object’s circular motion. Without centripetal force, an object would move in a straight line tangent to the circle.
To better understand the distinction between centripetal acceleration and centripetal force, let’s consider an example. Imagine you are driving a car around a curved road. As you turn the steering wheel, the car starts to change its direction. This change in direction is due to the centripetal acceleration acting on the car. The centripetal force, in this case, is provided by the friction between the car’s tires and the road surface. This frictional force pulls the car towards the center of the curved path, allowing it to maintain its circular motion.
Discussion of their roles and effects in circular motion
Both centripetal acceleration and centripetal force play crucial roles in circular motion. Let’s take a closer look at their effects and how they contribute to the overall motion of an object.
Centripetal acceleration is responsible for continuously changing the direction of an object’s velocity. In circular motion, an object’s velocity is always tangent to the circle at any given point. However, since the object is constantly changing its direction, its velocity vector is also changing. This change in velocity is what we refer to as centripetal acceleration. It is always directed towards the center of the circle and its magnitude can be calculated using the formula:
a = (v^2) / r
where “a” represents the centripetal acceleration, “v” is the object’s velocity, and “r” is the radius of the circular path.
Centripetal force, on the other hand, is the force that acts on an object to keep it moving in a circular path. It is directed towards the center of the circle and its magnitude depends on the mass of the object, its velocity, and the radius of the circular path. The centripetal force can be calculated using the formula:
F = (m * v^2) / r
where “F” represents the centripetal force, “m” is the mass of the object, “v” is its velocity, and “r” is the radius of the circular path.
In summary, centripetal acceleration is the acceleration that keeps an object moving in a circular path, while centripetal force is the force that acts on the object to maintain its circular motion. They are closely related and work together to ensure an object moves in a curved path rather than a straight line.
To further illustrate the difference between centripetal acceleration and centripetal force, let’s consider a simple example. Imagine swinging a ball attached to a string in a horizontal circle. The tension in the string provides the centripetal force required to keep the ball moving in a circular path. At the same time, the ball experiences centripetal acceleration, which constantly changes its direction towards the center of the circle.
In conclusion, centripetal acceleration and centripetal force are distinct concepts that are essential in understanding circular motion. While centripetal acceleration refers to the acceleration experienced by an object moving in a circular path, centripetal force is the force that acts on the object to maintain its circular motion. Together, they ensure that objects can move in curved paths and experience the fascinating phenomena of circular motion.
Centripetal Acceleration vs Linear Acceleration

Comparison of Centripetal Acceleration and Linear Acceleration
When it comes to the study of motion, two important concepts that often come up are centripetal acceleration and linear acceleration. While they both deal with the idea of acceleration, they have some key differences that set them apart. Let’s take a closer look at how centripetal acceleration and linear acceleration compare to each other.
Centripetal acceleration refers to the acceleration experienced by an object moving in a circular path. It is always directed towards the center of the circle and is responsible for keeping the object in its circular motion. On the other hand, linear acceleration refers to the acceleration experienced by an object moving in a straight line. It can be in any direction, depending on the forces acting on the object.
One way to understand the difference between centripetal acceleration and linear acceleration is to consider the direction of the acceleration. Centripetal acceleration always points towards the center of the circle, while linear acceleration can be in any direction. This means that centripetal acceleration is always perpendicular to the velocity of the object, while linear acceleration can be parallel or perpendicular to the velocity.
Explanation of their Differences in Terms of Direction and Motion
Another way to differentiate between centripetal acceleration and linear acceleration is to consider the motion of the object. Centripetal acceleration is responsible for changing the direction of an object’s motion, while linear acceleration is responsible for changing the speed of an object’s motion.
For example, imagine a car moving in a circular path on a racetrack. The car experiences centripetal acceleration, which keeps it moving in a circle. This acceleration is provided by the friction between the car’s tires and the track. The centripetal acceleration allows the car to continuously change its direction as it goes around the track.
On the other hand, if the car were to speed up or slow down while moving in a straight line, it would experience linear acceleration. This acceleration can be caused by pressing the gas pedal to increase speed or applying the brakes to decrease speed. Linear acceleration affects the car’s velocity, either by increasing or decreasing it.
In summary, centripetal acceleration and linear acceleration differ in terms of their direction and the type of motion they affect. Centripetal acceleration always points towards the center of the circle and is responsible for changing the direction of an object’s motion in a circular path. Linear acceleration, on the other hand, can be in any direction and is responsible for changing the speed of an object’s motion in a straight line.
Understanding the differences between centripetal acceleration and linear acceleration is crucial in various fields, such as physics, engineering, and sports. By grasping these concepts, we can better analyze and predict the behavior of objects in different types of motion.
Centripetal Acceleration vs Centrifugal Force
Differentiating between centripetal acceleration and centrifugal force
When discussing circular motion, two terms often come up: centripetal acceleration and centrifugal force. While they may seem similar, they are actually quite different. Let’s take a closer look at each of them.
Centripetal Acceleration
Centripetal acceleration refers to the acceleration experienced by an object moving in a circular path. It is always directed towards the center of the circle and is responsible for keeping the object moving in its circular trajectory. In other words, it is the acceleration that keeps an object from flying off in a straight line.
To understand centripetal acceleration, we need to consider the concept of velocity. Velocity is a vector quantity that includes both speed and direction. In circular motion, the direction of the velocity is constantly changing as the object moves around the circle. This change in direction results in a change in velocity, which in turn leads to acceleration.
Centrifugal Force
On the other hand, centrifugal force is often referred to as a “fictitious force” because it is not a real force in the traditional sense. Instead, it is a perceived force that appears to push an object away from the center of the circle. This apparent force is experienced by an object moving in a circular path and is equal in magnitude but opposite in direction to the centripetal force.
The centrifugal force is a result of inertia, which is the tendency of an object to resist changes in its state of motion. As an object moves in a circular path, it wants to continue moving in a straight line due to its inertia. The centrifugal force is the perceived force that arises from this tendency to move in a straight line.
Understanding their relationship and the concept of fictitious forces
Now that we have a basic understanding of centripetal acceleration and centrifugal force, let’s explore their relationship and the concept of fictitious forces.
As mentioned earlier, centripetal acceleration is the real acceleration experienced by an object moving in a circular path. It is responsible for changing the direction of the object’s velocity and keeping it on its circular trajectory. Without centripetal acceleration, the object would simply move in a straight line.
On the other hand, centrifugal force is not a real force but rather a perceived force that arises from the object’s tendency to move in a straight line. It is equal in magnitude but opposite in direction to the centripetal force. While the centrifugal force does not actually exist, it is a useful concept in understanding the dynamics of circular motion.
It is important to note that centripetal acceleration and centrifugal force are two sides of the same coin. They are interconnected and dependent on each other. Without centripetal acceleration, there would be no centrifugal force, and vice versa.
In summary, centripetal acceleration is the real acceleration that keeps an object moving in a circular path, while centrifugal force is the perceived force that appears to push the object away from the center of the circle. Understanding the relationship between these two concepts is crucial in comprehending the dynamics of circular motion.
Equivalence of Centripetal and Tangential Acceleration
Exploring the conditions under which centripetal acceleration and tangential acceleration are equal
When studying circular motion, we often come across two types of acceleration: centripetal acceleration and tangential acceleration. These two terms might sound complex, but they are actually quite straightforward once we break them down.
Centripetal acceleration refers to the acceleration experienced by an object moving in a circular path. It is always directed towards the center of the circle and is responsible for keeping the object in its circular trajectory. On the other hand, tangential acceleration is the acceleration that occurs along the tangent of the circular path. It is responsible for changing the object’s speed as it moves around the circle.
At first glance, it might seem that centripetal and tangential acceleration are two separate entities with different magnitudes and directions. However, under certain conditions, these two accelerations can be equal. Let’s explore these conditions further.
To understand when centripetal and tangential acceleration are equal, we need to consider the specific scenario in which an object is moving in a circular path. In this scenario, the object’s speed remains constant, meaning there is no change in its magnitude. This condition is crucial because it allows the tangential acceleration to be zero.
When the tangential acceleration is zero, the only acceleration acting on the object is the centripetal acceleration. Since the object is moving in a circular path, the centripetal acceleration is directed towards the center of the circle. Therefore, in this particular case, the centripetal acceleration and tangential acceleration are equal in magnitude.
Discussion of the implications and significance of this equivalence
The equivalence between centripetal and tangential acceleration has significant implications in the study of circular motion. It allows us to simplify calculations and analyze the motion of objects in a more straightforward manner.
By recognizing that centripetal and tangential acceleration can be equal, we can focus solely on the centripetal acceleration when dealing with circular motion scenarios where the object’s speed remains constant. This simplification saves us from having to consider the tangential acceleration separately, making our calculations more efficient.
Moreover, understanding the equivalence between centripetal and tangential acceleration helps us grasp the underlying principles of circular motion. It highlights the fact that circular motion involves both a change in direction (centripetal acceleration) and a change in speed (tangential acceleration). This realization deepens our understanding of how objects move in circular paths and how different types of acceleration come into play.
In practical terms, this equivalence is particularly relevant in various fields such as physics, engineering, and even everyday scenarios. For example, when designing roller coasters or analyzing the motion of vehicles on curved roads, understanding the relationship between centripetal and tangential acceleration is crucial. It allows engineers to ensure the safety and efficiency of these systems by considering the appropriate forces and accelerations involved.
In conclusion, the equivalence between centripetal and tangential acceleration is a fundamental concept in the study of circular motion. It simplifies calculations, deepens our understanding of motion, and has practical applications in various fields. By recognizing this equivalence, we can approach circular motion problems with greater clarity and efficiency.
Importance of v^2/r in Centripetal Acceleration
Centripetal acceleration is a fundamental concept in physics that helps us understand the motion of objects moving in a circular path. It is defined as the acceleration experienced by an object moving in a circular path towards the center of that path. One of the key factors that determine the magnitude of centripetal acceleration is the term v^2/r, where v represents the velocity of the object and r is the radius of the circular path.
Explanation of the significance of v^2/r in the formula for centripetal acceleration
In order to understand the significance of v^2/r in the formula for centripetal acceleration, let’s break it down. The formula for centripetal acceleration is given by:
a = v^2/r
Here, v^2 represents the square of the velocity of the object, while r represents the radius of the circular path. The square of the velocity is used in the formula because it takes into account both the speed and the direction of the object’s motion.
The term v^2/r represents the rate at which the object’s velocity is changing with respect to the radius of the circular path. In other words, it tells us how quickly the object’s velocity is changing as it moves along the circular path. This is important because it helps us understand the force required to keep the object moving in a circular path.
Understanding its role in determining the magnitude of centripetal acceleration
The term v^2/r plays a crucial role in determining the magnitude of centripetal acceleration. As mentioned earlier, it represents the rate at which the object’s velocity is changing with respect to the radius of the circular path.
When the velocity of the object increases, the magnitude of centripetal acceleration also increases. This is because a higher velocity means that the object is moving faster along the circular path, and therefore, its velocity is changing at a faster rate.
On the other hand, when the radius of the circular path increases, the magnitude of centripetal acceleration decreases. This is because a larger radius means that the object has to cover a greater distance to complete one revolution, which in turn reduces the rate at which its velocity is changing.
To put it simply, the term v^2/r tells us how much centripetal acceleration is needed to keep an object moving in a circular path. The larger the value of v^2/r, the greater the centripetal acceleration required. Conversely, a smaller value of v^2/r indicates a lower centripetal acceleration.
In conclusion, the term v^2/r in the formula for centripetal acceleration is of utmost importance as it helps us understand the rate at which an object’s velocity is changing with respect to the radius of the circular path. By considering this term, we can determine the magnitude of centripetal acceleration required to keep an object moving in a circular path.
Conclusion
In conclusion, centripetal acceleration and acceleration are closely related but distinct concepts in physics. Centripetal acceleration refers to the acceleration experienced by an object moving in a circular path, always directed towards the center of the circle. On the other hand, acceleration is a more general term that refers to any change in velocity, including changes in speed or direction. While centripetal acceleration is a specific type of acceleration, it is important to note that not all acceleration is centripetal. Overall, understanding the difference between centripetal acceleration and acceleration is crucial for comprehending the motion of objects in circular paths and the broader concepts of acceleration in physics.
What is the difference between centripetal acceleration and instantaneous velocity?
Centripetal acceleration and instantaneous velocity are both concepts in physics that involve the motion of objects. However, they represent different aspects of an object’s movement. Centripetal acceleration refers to the acceleration experienced by an object moving in a circular path, while instantaneous velocity refers to the velocity of an object at a specific moment in time. To understand these concepts in more depth, it is important to explore the Difference between instantaneous velocity and acceleration. By studying this article, you can gain insights into the subtle distinctions between these two fundamental principles in physics.
Frequently Asked Questions
1. What is the difference between centripetal acceleration and centripetal force?
Centripetal acceleration refers to the acceleration experienced by an object moving in a circular path, while centripetal force is the force responsible for causing this acceleration towards the center of the circle.
2. How does centripetal acceleration work?
Centripetal acceleration works by continuously changing the direction of an object’s velocity, keeping it moving in a circular path. It is always directed towards the center of the circle.
3. Why is centripetal acceleration important?
Centripetal acceleration is important because it allows objects to move in circular paths. It is necessary to maintain the object’s motion and prevent it from moving in a straight line tangent to the circle.
4. When does centripetal acceleration occur in an object?
Centripetal acceleration occurs in an object whenever it moves in a circular path. It is present as long as the object is undergoing circular motion.
5. Where is centripetal acceleration directed?
Centripetal acceleration is always directed towards the center of the circle in which the object is moving. It acts as a centripetal force, pulling the object inward.
6. How does centripetal acceleration change with radius?
Centripetal acceleration is inversely proportional to the radius of the circular path. As the radius decreases, the centripetal acceleration increases, and vice versa.
7. What is the relationship between centripetal acceleration and angular velocity?
Centripetal acceleration is related to angular velocity through the equation: centripetal acceleration = angular velocity^2 * radius. This equation shows that an increase in angular velocity or radius leads to an increase in centripetal acceleration.
8. What is the difference between centripetal acceleration and radial acceleration?
Centripetal acceleration refers to the acceleration towards the center of the circle, while radial acceleration refers to the acceleration along the radius of the circle. Radial acceleration includes both centripetal and tangential components.
9. How does centripetal acceleration compare to gravitational acceleration?
Centripetal acceleration and gravitational acceleration are two different types of acceleration. Centripetal acceleration is the acceleration towards the center of the circular path, while gravitational acceleration is the acceleration due to gravity. They are not directly related to each other.
10. When are centripetal and tangential acceleration equal?
Centripetal and tangential acceleration are equal when an object is moving in a circular path at a constant speed. In this case, the tangential acceleration is zero, and all the acceleration is directed towards the center of the circle, resulting in centripetal acceleration.
Also Read:
- How to find normal force with mass and acceleration
- How to find acceleration in a pulley system
- How to find acceleration from distance
- Angular acceleration and centripetal acceleration
- How to find angular acceleration without time
- How to find acceleration from distance and time
- How to find acceleration kinematics
- How to find average acceleration
- How to find centripetal acceleration without radius
- What causes centripetal acceleration
I am Durva Dave, completed my post-graduation in Physics. Physics fascinates me a lot and I like in knowing the ‘Why’ and ‘How’ of everything that unfolds in our universe. I try to write my blogs in simple yet effective language so that it is easier for the reader to understand as well remember. I hope with my curiosity I am able to provide the readers for what their looking for through my blogs. Let’s connect through LinkedIn.