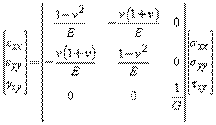What is shear strain?
Shear strain is the ratio of change in dimensions to the original dimension due to shear stress and deformation perpendicular rather than parallel to it. Shear strain results from the use of 2 parallel and opposite forces working at the surfaces of an object.
Shear strain formula:
Shear strain=ΔxL0/L.
Shear Modulus:
“This is the constant of proportion and is well-defined by the ratio of stress to strain.”
Shear modulus is generally represented by S.
S=shear-stress. / shear-strain.
Shear strain units:
This is dimensionless quantity, so this is Unitless.
Shear strain symbol:
Shear strain symbol=γ or ε
Shear strain unit:
1, or radian
Shear strain from axial strain
Strain:
Applied loads or displacements lead to change in dimensions. For the uniaxial displacement, the axial strain defined basically as the ratio of the variation in length to the actual length.
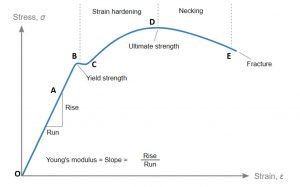
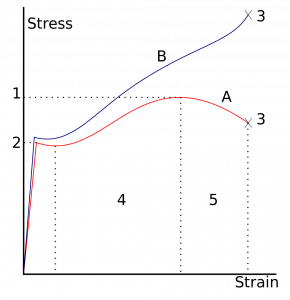
Shear stress strain diagram
The three-dimensional strain components may also be represented as simple axial strains and shear-strains. The displacement vectors (u,v,w) acting along the axes (x,y,z) respectively.
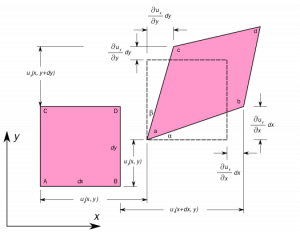
The uniaxial strain in x-direction due to displacement gradient,
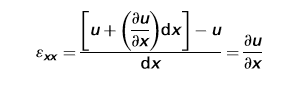
Similarly, the shear-strain in the y-direction due to displacement gradient is given by,

The shear-strain components are represented as strain matrix as following,

Three shear-strains are the strains represented in all planes in x,y,z directions as XY, YZ, XZ.
The strains are represented in the strain matrix-induced due to the stress:
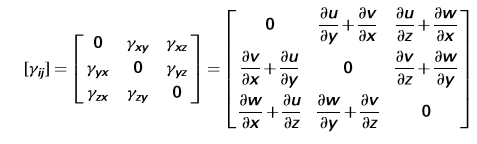
Strain Measurement:
It is difficult to measure stress directly. So, the strain measurement can be done using electric resistance circuit gauges connected to it.
Strain gauge measurement | Shear strain from a strain gauge
The strain gauge measurement is used to determine the resistance of the wire foiled together to the conducting substrate. The wire resistance is R,
\\frac{\\Delta R}{R}= K.\\varepsilon
where K recognized as strain-factor
Alternatively,
\\varepsilon= deformation = strain
so, strain can be induced by using strain measurement.
Since the strains are low, the Wheatstone bridge needs to determine the resistances. The galvanometer reading has to be zero to find out the resistances R1, R2, R3, R4. More than one configuration can be used to measure the strain. A half wiring can be used and attached to the other gauges. There are one active meter and one dummy meter. The dummy gauge reduces the temperature effects by canceling out them. Such difference can lead to an improvement in the accuracy of the circuits.
Maximum shear strain equation:
Maximum normal strain (εmax.)
(εx+εy)/2+(((εx-εy)/2)2+(γxy/2)2)0.5.
Minimum normal strain (εmin).
(εx+εy)/2-(((εx-εy)/2)2+(γxy/2)2)0.5.
Maximum shear-strain (in-plane) ( γmax (in-plane)).
((εx-εy)2+(γxy)2)0.5
Principal angle (θp)
[atan(γxy/(εx-εy))]/2
Principal shear strain:
Principal Stress:
Shear stress is zero at an alignment then principal stress happens.
Principal Angle:
This is the angle of alignment in that principal stress will occur for a definite point.
Principal Strain:
This is the highest and least normal strain possible for an material at that specific point and shear-strain is zero at the angle where principal strain occurs.
The 3 stresses normal to principal shear plane are termed principal-stress, where as in a plane where shear-strain is zero is termed as principal-strain.
Pure shear strain:
principal stress and strain are zero.
What is shear strain energy ?
Strain energy due to shear stress | Shear strain energy theory:
Maximum shear strain energy | Distortion energy (Von Mises) theory
The failure of utmost ductile material could have been determined by the shear stress theories or Von Mises theory as the failure occurs at the shearing of the materials. This theory can be represented as
(σ1−σ2)2+(σ2−σ3)2+(σ3−σ1)2=2σy2=constant
For σ3 = 0,
The yield locus is an ellipse similar to sheer diagonal. In3D Stress system, this equation states the surface of a prism with circular cross section. More precisely a cylinder with its central axis along the line σ1 = σ2 = σ3.
The axis cut-thru the principal stress’s origin, and it is inclined at equal angle. when σ3 = 0,
The failure condition for ellipse formed by the intersection of the (σ1, σ2) plane with the inclined cylinder.
Shear strain energy per unit volume theory.
As per von Mises theory in 3D,the yield locus will be at the surface of the inclined cylinder. Points inside the cylinder show the safe points, whereas the points outside the cylinder show the failure conditions. The cylinder axis along σ1 = σ2 = σ3 line termed the hydrostatic stress line. It shows that the hydrostatic stress alone cannot give yield. It considers all the conditions altogether and shows that all cylinder points are safe.
Shear strain example problems
- metal cutting
- painting brush
- Chewing gum
- In river water case, river bed will experience the shear stress because of water flow situations.
- During screen-sliding circumstance.
- To Polishing a surface.
- To write on surface, will experience shear-strain.
The following image of rectangular hut shows the deformation of rectangular into parallelogram due to shear-strain.

The reason behind shear strain:
Shear stress is the applied force that will cause deformation of a material by slippage along a plane or a plane parallel to the stress imposed on the surface of the object.
Relationship between shear stress and strain
Shear strain vs shear stress | shear strain vs shear force
The shear strain is the deformation caused due to shear stress. Shear stress is the stress occurred due to shear forces in-between the object’s parallel surfaces.
Torsional shear strain
Torsional shear-strain τ = shear stress (N/m2, Pa) T = applied torque (Nm)
The shear-strain is calculated by the angle of twist, the length, and the distance along the radius.
γ = shear strain (radians)
Shear stress strain curve:
Shear stress acts along the surface or parallel to the surface and may cause 1 layer to slide on others. shear stress leads to deforming the rectangular object into the parallelogram.
Shear stress acts to change the dimension and angle of the object.
Shear stress= F/A
Shear-strain: The shear-strain is the deformation amount to a given line rather than parallel.
Shear strain gamma
Shear-strain gamma= delta x/L.
The relationship between the shear stress and shear-strain for a specific material is acknowledged as that material’s shear.
Shear stress strain curve Yield stress
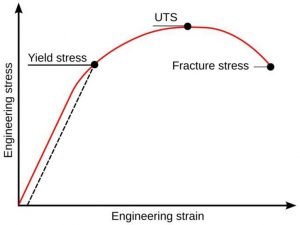
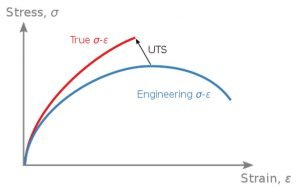
Stress Strain curve Engineering and True
Variation of shear stress with rate of deformation
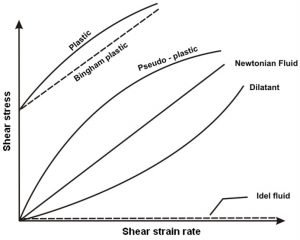
Shear stress-strain curves are a significant graphical measure.
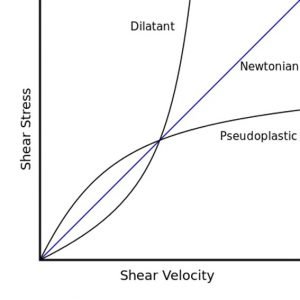
Shear Stress vs Shear velocity
Shear stress vs shear rate for dilatant and pseudoplastic non-Newtonian fluids compared to Newtonian fluid.

Octahedral shear strain:
The octahedral shear stress/ strain gives the yield point of elastic material under a general stress state. The material displays yielding when the octahedral shear stress reach the extreme value of stress/strain. This is equivalent acknowledged as Von Mises yield criteria.
Shear strain rate :
The strain is the ratio of change in the length to its original length, so; shear-strain is a dimensionless quantity, so the strain-rate is in inversed time unit.
Shear strain formula in metal cutting:
Shear Plane Angle:
This is the angle between the horizontal plane and the shear plane, Significant for shear-strain applications in metal cutting.
The shear-strain rate at the shear plane, ϒAB is a function of cutting velocity and feed.
Difference between shear stress and Shear strain
Shear stress vs Shear strain:
Shear stress contemplates a block, which is subjected to a set of equal and opposite forces Q and this block recognized as bi-cycle-brake-block linked to wheel.There is a chance that one layer of the body slides on others, during shear stress initiation. If this failure is not permitted, then a shear stress T will be formed.
Q – shear load shear stress (z) = area resisting shear A.
This shear stress will act on vertically to the area. The direct stresses will be at normal direction to the area of application though.
Considering bicycle brake block, the rectangular shaped blocks mightn’t be deformed after the baking force has been applied and block might change the shape in the form of strain.
The shear-strain is proportionate to the shear stress in the elastic range. The modulus of rigidity is represented as
shear stress z shear strain y = – = constant = G
The constant G = the modulus of rigidity or shear modulus
Why do edge dislocations in crystal lattices introduce compressive tensile and shear lattice strains while screw dislocations only introduce shear strains ?
Because observational and pedagogical definition prescribes the coordinate frames in which this is true”, is probably the most accurate answer.
There are several approaches to visualizing the behavior of the strain fields around dislocations. The first approach is by direct observation; the second one borrows concepts from fracture mechanics. Both are equivalent.
- An edge dislocation directed to the Burgers vector. Although a screw-dislocation directed perpendicularly to it.
- The screw-dislocation ‘unzip’ the lattice as it travels thru it, creating a ‘screw’ or helical prearrangement of atom around the core.
Shear strain problems:
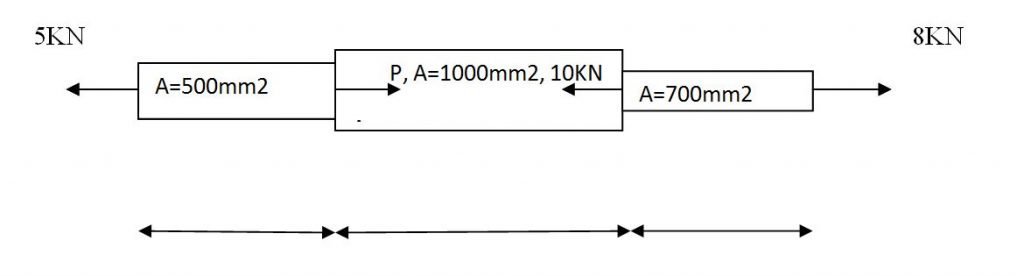
Problem : A rectangular block has area of 0.25m2. The height of the block is 10cm.A shearing force is applied to the top face of the block. And the displacement is 0.015mm.Find the stress, strain and shearing force. Modulus of rigidity= 2.5*10^10 N/m2
Given:
A= 0.25m2
H=10m
x=0.015mm
η =2.5*10^10N/m2.
Solution:
Shear strain = tan θ =X/H
=0.015*10^-3/10*10^-2
tan θ =1.5*10^-3
Modulus of Rigidity = Shear stress/Shear strain
2.5*10^10 = shear stress /0.0015
Shear stress =2.5*10^10*1.5*10^-3
=3.75*10^7 N/m2
Shear stress =F/A
F = 3.75*10^7*0.25
= 9.37*10^6 N.
Problem : A cube has side of 10 cm. The shearing force is applied on the upper side of the cube and the displacement is 0.75 cm by force of 0.25N. Calculate modulus of rigidity of the substance.
Given:
A= 10*10= 100 cm2
F=0.25N
H= 5cm
X=0.75cm
As we know,
Modulus of rigidity = Shear stress/Shear strain
Shear-strain is= X/H
=0.75/5
= 0.15
Shear Stress= F/A
= 0.25/100*10^-4
=25N.
Modulus of Rigidity = 25/0.15
= 166.7 N/m^2
For more articles click here


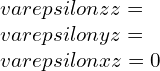

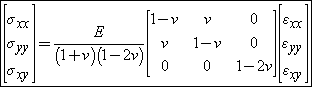
 is represented as,
is represented as,