Sangeeta Das

How to Calculate Mass Flow Rate

Introduction

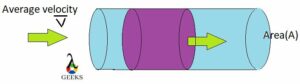
When it comes to fluid dynamics, understanding how to calculate mass flow rate is crucial. Mass flow rate is a fundamental concept in engineering and thermodynamics that measures the amount of mass passing through a given point in a system per unit of time. It is an essential parameter in various applications, including pipe flow, nozzle design, and flowmeter calibration.

Definition and Notation

Before diving into the calculation of mass flow rate, let’s define some key terms and notation. Mass flow rate, denoted as ṁ, is the mass of a substance flowing through a given cross-sectional area per unit of time. It is typically measured in kilograms per second (kg/s) or other mass units per time unit.

To calculate the mass flow rate, we need to consider the density of the fluid, the velocity of the fluid, and the cross-sectional area through which the fluid is flowing. The formula for mass flow rate is:

ṁ = ρ * A * V

Where:
– ṁ is the mass flow rate
– ρ is the density of the fluid
– A is the cross-sectional area
– V is the velocity of the fluid

Calculation of Mass Flow Rate

To calculate the mass flow rate, we need to know the density of the fluid, the velocity of the fluid, and the cross-sectional area. Let’s break down the steps involved in calculating the mass flow rate:

1. Determine the density of the fluid: The density of the fluid can be obtained from reference tables or measured using specialized instruments. It is typically expressed in kilograms per cubic meter (kg/m³).

2. Measure the velocity of the fluid: The velocity of the fluid can be measured using various techniques, such as flowmeters or pitot tubes. It is crucial to ensure accurate velocity measurements for precise mass flow rate calculations.

3. Determine the cross-sectional area: The cross-sectional area refers to the area through which the fluid is flowing. It can be calculated using geometric formulas or measured directly using appropriate instruments.

4. Plug the values into the formula: Once you have obtained the density, velocity, and cross-sectional area, you can plug these values into the mass flow rate formula: ṁ = ρ * A * V. Calculate the product of the density, cross-sectional area, and velocity to obtain the mass flow rate.

Importance of Accurate Measurement

Accurate measurement of mass flow rate is crucial in many engineering applications. It allows engineers to understand and control the flow of fluids in various systems. Whether it’s optimizing the performance of a chemical process or designing efficient HVAC systems, accurate mass flow rate measurement ensures proper operation and prevents potential issues.

By accurately calculating the mass flow rate, engineers can make informed decisions regarding system design, equipment sizing, and process optimization. It enables them to identify potential bottlenecks, optimize energy consumption, and ensure the safety and reliability of the system.

Factors Affecting Mass Flow Rate

Several factors can affect the mass flow rate of a fluid. Understanding these factors is essential for accurate calculations and system design. Here are some key factors that influence mass flow rate:

1. Fluid properties: The density and viscosity of the fluid play a significant role in determining the mass flow rate. Different fluids have different densities and viscosities, which affect their flow characteristics.

2. Cross-sectional area: The size and shape of the cross-sectional area through which the fluid is flowing directly impact the mass flow rate. A larger area allows for a higher flow rate, while a smaller area restricts the flow.

3. Velocity: The velocity of the fluid is a critical factor in determining the mass flow rate. Higher velocities result in higher mass flow rates, while lower velocities lead to lower flow rates.

4. Pressure: Pressure differentials across a system can affect the mass flow rate. Higher pressure differentials can increase the flow rate, while lower differentials can restrict it.

5. Temperature: Changes in temperature can affect the density and viscosity of the fluid, thereby impacting the mass flow rate. It is essential to consider temperature variations when calculating mass flow rate.

By taking these factors into account and accurately calculating the mass flow rate, engineers can ensure the efficient and reliable operation of various systems.

In conclusion, understanding how to calculate mass flow rate is essential in fluid dynamics and engineering. By considering the density, velocity, and cross-sectional area, engineers can accurately determine the mass flow rate of a fluid. Accurate measurement of mass flow rate is crucial for system design, optimization, and ensuring the proper functioning of various processes. By considering factors such as fluid properties, cross-sectional area, velocity, pressure, and temperature, engineers can make informed decisions and achieve desired outcomes in their applications.

How to Calculate Mass Flow Rate from Volumetric Flow Rate

Definition and Calculation of Volumetric Flow Rate

When it comes to fluid dynamics, understanding the concept of volumetric flow rate is essential. Volumetric flow rate refers to the amount of fluid that passes through a given point in a specified amount of time. It is commonly denoted as Q and is measured in units such as cubic meters per second (m³/s) or liters per minute (L/min).

To calculate the volumetric flow rate, you need to know the cross-sectional area of the flow and the velocity of the fluid. The formula to calculate volumetric flow rate is:

Volumetric Flow Rate (Q) = Cross-sectional Area (A) × Velocity (V)

The cross-sectional area is the area perpendicular to the direction of flow, and the velocity is the speed at which the fluid is moving. By multiplying these two values together, you can determine the volumetric flow rate.

Relationship between Mass Flow Rate and Volumetric Flow Rate

While volumetric flow rate provides information about the volume of fluid passing through a point, mass flow rate gives insight into the mass of fluid passing through that same point. Mass flow rate is denoted as m-dot and is measured in units such as kilograms per second (kg/s) or pounds per minute (lb/min).

To calculate the mass flow rate, you need to consider not only the volumetric flow rate but also the density of the fluid. The formula to calculate mass flow rate is:

Mass Flow Rate (m-dot) = Volumetric Flow Rate (Q) × Density (ρ)

The density of a fluid is a measure of its mass per unit volume. It is typically denoted as ρ and is measured in units such as kilograms per cubic meter (kg/m³) or pounds per cubic foot (lb/ft³). By multiplying the volumetric flow rate by the density, you can determine the mass flow rate.

It’s important to note that the relationship between mass flow rate and volumetric flow rate depends on the density of the fluid. Different fluids have different densities, so the same volumetric flow rate can correspond to different mass flow rates depending on the fluid being considered.

In engineering and various fields of science, calculating mass flow rate from volumetric flow rate is crucial for understanding fluid behavior, designing systems, and ensuring proper measurements. By applying the principles of fluid mechanics and thermodynamics, engineers and scientists can accurately determine mass flow rates in pipes, nozzles, orifices, and other flow systems.

In summary, the mass flow rate can be calculated from the volumetric flow rate by multiplying it by the density of the fluid. Understanding this relationship is fundamental in fluid dynamics and plays a vital role in various engineering and scientific applications.

How to Calculate Mass Flow Rate from Pressure Gradient

Introduction to Pressure Gradient

In fluid dynamics, the pressure gradient refers to the change in pressure over a given distance in a fluid. It plays a crucial role in understanding the flow behavior of fluids in various engineering applications. When there is a pressure difference within a fluid, it creates a force that drives the fluid to move from an area of high pressure to an area of low pressure. This phenomenon is known as fluid flow.

Hagen Poiseuille Equation

To calculate the mass flow rate from a pressure gradient, we can utilize the Hagen Poiseuille equation. This equation is derived from the principles of fluid mechanics and is particularly useful for calculating the flow rate of viscous fluids through pipes, orifices, and nozzles.

The Hagen Poiseuille equation relates the pressure gradient, fluid viscosity, and the geometry of the flow system. It can be expressed as follows:

Where:
– Q is the volume flow rate
– ΔP is the pressure gradient
– η is the dynamic viscosity of the fluid
– L is the length of the flow path
– A is the cross-sectional area of the flow path

Calculation of Mass Flow Rate from Pressure Gradient

To calculate the mass flow rate from a given pressure gradient, we need to consider the density of the fluid. The mass flow rate is the measure of the mass of fluid passing through a given point per unit time. It can be calculated by multiplying the volume flow rate by the density of the fluid.

The volume flow rate (Q) can be determined using the Hagen Poiseuille equation. Once we have the volume flow rate, we can calculate the mass flow rate (M) using the following equation:

Where:
– M is the mass flow rate
– Q is the volume flow rate
– ρ is the density of the fluid

By incorporating the density of the fluid into the calculation, we can accurately determine the mass flow rate from a given pressure gradient.

Example Calculation

Let’s consider an example to illustrate the calculation of mass flow rate from a pressure gradient. Suppose we have a fluid flowing through a pipe with a pressure gradient of 100 Pa/m. The fluid has a dynamic viscosity of 0.01 Pa·s and a density of 1000 kg/m³. The length of the pipe is 10 m, and the cross-sectional area is 0.1 m².

Using the Hagen Poiseuille equation, we can calculate the volume flow rate (Q):

Substituting the given values into the equation, we get:

Now, we can calculate the mass flow rate (M) by multiplying the volume flow rate by the density:

Therefore, the mass flow rate of the fluid through the pipe is 98 kg/s.

Conclusion

In conclusion, the mass flow rate can be calculated from a pressure gradient by utilizing the Hagen Poiseuille equation and considering the density of the fluid. By understanding the principles of fluid dynamics and applying the appropriate equations, engineers and scientists can accurately determine the mass flow rate in various fluid flow systems.

How to Calculate Mass Flow Rate of Fuel in an Engine

Fuel mass flow rate is an essential parameter to consider when analyzing the performance of an engine. By accurately calculating the mass flow rate of fuel, engineers and technicians can gain valuable insights into the efficiency and effectiveness of the engine’s fuel consumption. In this section, we will explore the importance of calculating fuel mass flow rate, the formula used for its calculation, and the calculation of Brake Specific Fuel Consumption (BSFC) and Indicated Specific Fuel Consumption (ISFC).

Importance of Calculating Fuel Mass Flow Rate

The mass flow rate of fuel is a crucial factor in understanding the overall efficiency of an engine. It provides valuable information about the amount of fuel consumed per unit of time, allowing engineers to evaluate the engine’s performance and make necessary adjustments for optimal operation.

By accurately calculating the fuel mass flow rate, engineers can determine the engine’s fuel efficiency and identify any potential issues or areas for improvement. This information is particularly valuable in the automotive industry, where fuel consumption plays a significant role in both environmental impact and cost-effectiveness.

Formula for Fuel Mass Flow Rate

The mass flow rate of fuel can be calculated using a simple formula that takes into account the volume flow rate, density, and velocity of the fuel. The formula is as follows:

Mass Flow Rate = Volume Flow Rate x Density

To calculate the volume flow rate, you need to multiply the cross-sectional area of the flow by the velocity of the fuel. The density of the fuel can be obtained from reference tables or by measuring it directly.

Calculation of BSFC and ISFC

Brake Specific Fuel Consumption (BSFC) and Indicated Specific Fuel Consumption (ISFC) are two important metrics used to evaluate the fuel efficiency of an engine.

BSFC is a measure of the amount of fuel consumed per unit of power produced by the engine. It is calculated by dividing the fuel mass flow rate by the power output of the engine. The units of BSFC are typically in grams per kilowatt-hour (g/kWh).

ISFC, on the other hand, is a measure of the amount of fuel consumed per unit of work done within the engine cylinder. It is calculated by dividing the fuel mass flow rate by the indicated power output of the engine. The units of ISFC are also typically in grams per kilowatt-hour (g/kWh).

Both BSFC and ISFC provide valuable information about the fuel efficiency of an engine. By monitoring these metrics and making adjustments to the engine’s operation, engineers can optimize fuel consumption and reduce environmental impact.

In conclusion, calculating the mass flow rate of fuel in an engine is essential for evaluating its performance and fuel efficiency. By understanding the importance of this calculation, utilizing the appropriate formula, and considering metrics such as BSFC and ISFC, engineers can make informed decisions to improve the overall efficiency of the engine.

How to Calculate Mass Flow Rate of Air in an Engine

Measurement of Air Flow Rate

When it comes to understanding the performance of an engine, one crucial parameter to consider is the mass flow rate of air. The mass flow rate of air refers to the amount of air that passes through the engine per unit of time. This measurement is essential for various applications, including engineering, thermodynamics, and fluid mechanics.

To accurately determine the mass flow rate of air in an engine, it is necessary to measure the volume flow rate, density, and velocity of the air. These measurements can be obtained using different techniques and instruments, depending on the specific requirements of the engine and the available resources.

Here are some common methods used to measure air flow rate:

1. Flowmeters: Flowmeters are devices specifically designed to measure the flow rate of a fluid, including air. There are various types of flowmeters available, such as orifice meters, venturi meters, and magnetic flowmeters. These instruments utilize different principles to measure the flow rate accurately.

2. Pitot Tubes: Pitot tubes are simple yet effective devices used to measure the velocity of a fluid. They consist of a small tube with one end pointed directly into the fluid flow and the other end connected to a pressure gauge. By measuring the pressure difference between the two ends of the tube, the velocity of the fluid can be determined.

3. Anemometers: Anemometers are handheld devices commonly used to measure wind speed. However, they can also be used to measure air flow rate in engines. Anemometers typically utilize rotating cups or propellers to determine the velocity of the air, which can then be used to calculate the mass flow rate.

Formula for Air Mass Flow Rate

Once the necessary measurements of volume flow rate, density, and velocity have been obtained, the mass flow rate of air can be calculated using a simple formula. The formula for calculating the mass flow rate is as follows:

Mass Flow Rate = Volume Flow Rate x Density

The volume flow rate represents the amount of air passing through the engine per unit of time, usually measured in cubic meters per second (m³/s). The density of the air is the mass of the air per unit volume, typically measured in kilograms per cubic meter (kg/m³).

By multiplying the volume flow rate by the density, we obtain the mass flow rate of air. This value represents the actual mass of air passing through the engine per unit of time and is crucial for understanding the engine’s performance and efficiency.

It is important to note that the units used in the calculations should be consistent. For example, if the volume flow rate is measured in cubic feet per minute (CFM), it should be converted to cubic meters per second (m³/s) before calculating the mass flow rate.

In conclusion, calculating the mass flow rate of air in an engine is a fundamental aspect of understanding its performance. By accurately measuring the volume flow rate, density, and velocity of the air, and applying the appropriate formula, engineers and researchers can gain valuable insights into the engine’s efficiency and make informed decisions for optimization and improvement.

How to Calculate Mass Flow Rate of Dry Air

To understand how to calculate the mass flow rate of dry air, we need to start by defining what mass flow rate is. Mass flow rate is a fundamental concept in fluid dynamics that measures the amount of mass passing through a given point per unit of time. In the case of dry air, it refers to the amount of air passing through a specific location in a system.

Calculation of Mass Flow Rate of Dry Air

Calculating the mass flow rate of dry air involves considering several factors, such as the volume flow rate, density, and velocity of the air. The formula for calculating mass flow rate is:

Mass Flow Rate = Volume Flow Rate x Density

Let’s break down each component of the formula and understand how to calculate them.

1. Volume Flow Rate

The volume flow rate represents the volume of air passing through a given point per unit of time. It is usually measured in cubic meters per second (m³/s) or cubic feet per minute (CFM). To calculate the volume flow rate, you need to know the cross-sectional area of the flow and the velocity of the air.

The formula for volume flow rate is:

Volume Flow Rate = Cross-sectional Area x Velocity

To find the cross-sectional area, you can measure the dimensions of the pipe, duct, or any other conduit through which the air is flowing. Once you have the cross-sectional area, you need to determine the velocity of the air. This can be done using various methods, such as using a flowmeter or calculating it based on the pressure difference across a nozzle or an orifice.

2. Density

Density is a measure of how much mass is contained in a given volume of a substance. In the case of dry air, density is affected by factors such as temperature, pressure, and humidity. However, for simplicity, we will assume that the air is at a constant temperature and pressure.

The density of dry air can be calculated using the ideal gas law:

Density = (Pressure x Molecular Weight) / (Gas Constant x Temperature)

Where:
– Pressure is the absolute pressure of the air in Pascals (Pa)
– Molecular Weight is the molar mass of dry air, which is approximately 28.97 grams per mole (g/mol)
– Gas Constant is the ideal gas constant, which is approximately 8.314 J/(mol·K)
– Temperature is the absolute temperature of the air in Kelvin (K)

3. Calculation

Now that we have the volume flow rate and the density, we can calculate the mass flow rate of dry air by multiplying the two values together:

Mass Flow Rate = Volume Flow Rate x Density

It’s important to note that the units used for each component of the calculation should be consistent. For example, if the volume flow rate is measured in cubic meters per second (m³/s) and the density is in kilograms per cubic meter (kg/m³), the resulting mass flow rate will be in kilograms per second (kg/s).

By calculating the mass flow rate of dry air, we can gain valuable insights into various engineering and thermodynamic applications. Understanding the mass flow rate is crucial for designing efficient HVAC systems, optimizing combustion processes, and analyzing fluid mechanics in a wide range of industries.

In conclusion, calculating the mass flow rate of dry air involves determining the volume flow rate and the density of the air. By using the appropriate formulas and units, engineers and scientists can accurately quantify the amount of air passing through a specific point in a system. This knowledge is essential for designing and optimizing various processes that rely on the flow of dry air.

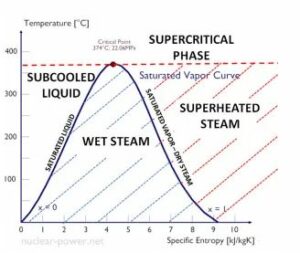
How to Calculate Mass Flow Rate of Steam

To calculate the mass flow rate of steam, we need to understand the basic principles of fluid dynamics and conservation of mass. Mass flow rate is a fundamental concept in engineering, thermodynamics, and fluid mechanics, and it plays a crucial role in various applications such as nozzle design, pipe flow analysis, orifice sizing, and flowmeter calibration.

Formula for Steam Mass Flow Rate

The mass flow rate of steam can be calculated using the equation:

Mass Flow Rate = Volume Flow Rate x Density

The volume flow rate represents the amount of steam passing through a given cross-sectional area per unit time, while the density is the mass per unit volume of the steam. By multiplying these two values, we can determine the mass flow rate of steam.

To calculate the volume flow rate, we can use the equation:

Volume Flow Rate = Velocity x Cross-Sectional Area

The velocity represents the speed at which the steam is flowing, while the cross-sectional area is the area perpendicular to the direction of flow. By multiplying these two values, we can determine the volume flow rate of steam.

Units and Measurements

When calculating the mass flow rate of steam, it is essential to ensure that the units are consistent. The most commonly used unit for mass flow rate is kilograms per second (kg/s). However, other units such as pounds per hour (lb/hr) or grams per minute (g/min) may also be used depending on the specific application.

Similarly, the units for volume flow rate can vary, with cubic meters per second (m³/s) being the standard SI unit. Other units such as cubic feet per minute (cfm) or liters per minute (L/min) are also commonly used.

To obtain accurate results, it is crucial to measure the velocity and cross-sectional area correctly. Various techniques and instruments, such as Pitot tubes, flowmeters, orifice plates, and ultrasonic flowmeters, can be used to measure these parameters accurately.

Example Calculation

Let’s consider an example to illustrate the calculation of the mass flow rate of steam. Suppose we have a steam pipe with a velocity of 10 m/s and a cross-sectional area of 0.5 m². The density of the steam is 2 kg/m³.

First, we calculate the volume flow rate:

Volume Flow Rate = Velocity x Cross-Sectional Area
= 10 m/s x 0.5 m²
= 5 m³/s

Next, we calculate the mass flow rate:

Mass Flow Rate = Volume Flow Rate x Density
= 5 m³/s x 2 kg/m³
= 10 kg/s

Therefore, the mass flow rate of steam in this example is 10 kg/s.

Conclusion

Calculating the mass flow rate of steam is a fundamental concept in fluid dynamics and thermodynamics. By understanding the principles of conservation of mass and using the appropriate equations, we can accurately determine the mass flow rate of steam. It is crucial to ensure consistent units and accurate measurements of velocity and cross-sectional area to obtain reliable results.

How to Calculate Mass Flow Rate of Exhaust Gas

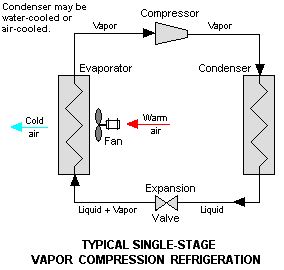
Importance of Exhaust Gas Mass Flow Rate

When it comes to understanding and optimizing the performance of engines and exhaust systems, calculating the mass flow rate of exhaust gas is of utmost importance. The mass flow rate provides crucial information about the amount of exhaust gas being expelled from the system per unit of time. By accurately determining the mass flow rate, engineers and researchers can evaluate the efficiency of combustion processes, assess emissions, and design effective exhaust systems.

The mass flow rate of exhaust gas is particularly significant in the automotive industry, where it plays a vital role in meeting emission standards and improving fuel efficiency. It helps engineers identify potential issues such as incomplete combustion, excessive emissions, or restricted flow, allowing them to make necessary adjustments to enhance engine performance and reduce environmental impact.

Calculation of Exhaust Gas Mass Flow Rate

To calculate the mass flow rate of exhaust gas, we need to consider several factors, including the volume flow rate, density, and velocity of the gas. The equation used to calculate mass flow rate is:

Mass Flow Rate = Volume Flow Rate x Density

Let’s break down the steps involved in calculating the mass flow rate:

1. Determine the Volume Flow Rate:
   The volume flow rate represents the amount of gas passing through a given point in the system per unit of time. It is typically measured in cubic meters per second (m³/s) or cubic feet per minute (CFM). To calculate the volume flow rate, you can use various methods such as flowmeters, orifice plates, or differential pressure devices.

2. Determine the Density:
   The density of the gas is a measure of its mass per unit volume. It is typically expressed in kilograms per cubic meter (kg/m³) or pounds per cubic foot (lb/ft³). The density of exhaust gas depends on factors such as temperature, pressure, and composition. It can be obtained from gas property tables or calculated using equations based on the ideal gas law.

3. Calculate the Mass Flow Rate:
   Once you have the volume flow rate and density, you can multiply them together to obtain the mass flow rate. The resulting value will be expressed in kilograms per second (kg/s) or pounds per minute (lb/min), depending on the units used for volume flow rate and density.

It is important to note that the mass flow rate remains constant throughout a closed system, in accordance with the principle of conservation of mass. This means that regardless of changes in velocity or cross-sectional area, the mass flow rate will remain the same as long as there are no additions or subtractions of mass within the system.

In engineering and thermodynamics, accurately calculating the mass flow rate of exhaust gas is crucial for designing efficient systems, optimizing performance, and meeting regulatory requirements. By understanding the principles and equations involved, engineers can make informed decisions to improve the overall efficiency and environmental impact of exhaust systems.

How to Calculate Mass Flow Rate of Gas

Calculation of Mass Flow Rate of Gas

When it comes to fluid dynamics, calculating the mass flow rate of a gas is an essential task. Mass flow rate refers to the amount of mass that passes through a given point per unit of time. It is a crucial parameter in various fields, including engineering, thermodynamics, and fluid mechanics. In this section, we will explore how to calculate the mass flow rate of a gas and understand the underlying principles.

To calculate the mass flow rate of a gas, we need to consider a few key factors: the volume flow rate, density, and velocity of the gas. The equation for mass flow rate is derived from the principle of conservation of mass, which states that mass cannot be created or destroyed, only transferred or transformed.

The equation for mass flow rate is as follows:

Mass Flow Rate = Volume Flow Rate x Density

Let’s break down each component of the equation to understand how to calculate the mass flow rate of a gas.

Volume Flow Rate

The volume flow rate refers to the volume of gas that passes through a given point per unit of time. It is typically measured in cubic meters per second (m³/s) or cubic feet per minute (CFM). To calculate the volume flow rate, we need to multiply the cross-sectional area of the flow by the velocity of the gas.

Volume Flow Rate = Cross-Sectional Area x Velocity

Density

Density is a measure of how much mass is contained in a given volume of a substance. In the context of gas flow, density is typically measured in kilograms per cubic meter (kg/m³) or pounds per cubic foot (lb/ft³). The density of a gas depends on various factors, including temperature and pressure. It can be calculated using the ideal gas law or obtained from reference tables.

Velocity

Velocity refers to the speed at which the gas is flowing. It is typically measured in meters per second (m/s) or feet per second (ft/s). The velocity of a gas can be determined using various methods, such as using a flowmeter, measuring the pressure difference across a nozzle or orifice, or using Bernoulli’s equation.

Once we have determined the volume flow rate, density, and velocity of the gas, we can plug these values into the equation for mass flow rate to calculate the desired parameter.

Units and Measurement

When calculating the mass flow rate of a gas, it is crucial to ensure that all the units are consistent. For example, if the volume flow rate is measured in cubic meters per second, the density should be in kilograms per cubic meter, and the resulting mass flow rate will be in kilograms per second. It is essential to convert units if necessary to maintain consistency and accuracy in the calculations.

In engineering and scientific applications, precise measurements are crucial. Therefore, it is essential to use accurate instruments and techniques to measure the various parameters involved in calculating the mass flow rate of a gas. Flowmeters, pressure sensors, and temperature sensors are commonly used tools in these measurements.

Understanding how to calculate the mass flow rate of a gas is fundamental in many engineering and scientific disciplines. By considering the volume flow rate, density, and velocity of the gas, we can determine the amount of mass that passes through a given point per unit of time. This knowledge is invaluable in designing and optimizing systems that involve gas flow, such as pipelines, nozzles, and ventilation systems.

How to Calculate Mass Flow Rate of Refrigerant

Determining Refrigerating Capacity

When it comes to refrigeration systems, understanding the mass flow rate of the refrigerant is crucial for efficient operation. The mass flow rate refers to the amount of refrigerant that passes through a specific point in the system per unit of time. By calculating the mass flow rate, engineers and technicians can determine the refrigerating capacity of the system and make informed decisions regarding its performance and efficiency.

To determine the refrigerating capacity, several factors need to be considered. These include the specific heat capacity of the refrigerant, the temperature difference across the evaporator or condenser, and the rate at which heat is transferred. By analyzing these factors, it becomes possible to calculate the mass flow rate of the refrigerant accurately.

Calculation of Mass Flow Rate of Refrigerant

To calculate the mass flow rate of the refrigerant, engineers and technicians rely on a combination of fluid dynamics principles and thermodynamic equations. The mass flow rate can be determined using the equation:

Mass Flow Rate = Volume Flow Rate x Density

The volume flow rate refers to the volume of refrigerant passing through a given point in the system per unit of time. It can be calculated using the equation:

Volume Flow Rate = Velocity x Cross-sectional Area

The velocity represents the speed at which the refrigerant is flowing, while the cross-sectional area refers to the area through which the refrigerant is passing. By multiplying these two values, the volume flow rate can be obtained.

The density of the refrigerant is a crucial parameter in the calculation. It represents the mass per unit volume of the refrigerant and can vary depending on factors such as temperature and pressure. To determine the density, engineers and technicians often rely on tables or equations specific to the refrigerant being used.

Once the volume flow rate and density are known, the mass flow rate can be calculated by multiplying these two values together. The resulting value represents the amount of refrigerant passing through the system per unit of time and is typically measured in kilograms per second (kg/s) or pounds per second (lb/s).

It is important to note that the mass flow rate is subject to the principle of conservation of mass. This principle states that mass cannot be created or destroyed but can only be transferred or transformed. Therefore, the mass flow rate entering a specific point in the system must be equal to the mass flow rate exiting that point.

In practical applications, engineers and technicians often use various measurement devices such as flowmeters, nozzles, orifices, or pressure sensors to determine the relevant parameters required for calculating the mass flow rate. These devices provide accurate readings and allow for precise calculations, ensuring the efficient operation of refrigeration systems.

In conclusion, calculating the mass flow rate of refrigerant is essential for understanding the performance and efficiency of refrigeration systems. By considering factors such as the specific heat capacity, temperature difference, and heat transfer rate, engineers and technicians can accurately determine the refrigerating capacity. Using fluid dynamics principles and thermodynamic equations, the mass flow rate can be calculated by multiplying the volume flow rate and density of the refrigerant. This information enables informed decision-making and optimization of refrigeration systems for maximum efficiency.

How to Calculate Mass Flow Rate of Dry Air

To calculate the mass flow rate of dry air, we need to understand the basic principles of fluid dynamics and the equation that governs mass flow rate. Mass flow rate is a fundamental concept in engineering, thermodynamics, and fluid mechanics, and it is crucial for various applications such as designing pipes, nozzles, orifices, and flowmeters.

Calculation of Mass Flow Rate of Dry Air

The mass flow rate of a fluid is defined as the amount of mass passing through a given cross-sectional area per unit time. In the case of dry air, we can calculate the mass flow rate using the equation:

Mass Flow Rate (ṁ) = Density (ρ) x Volume Flow Rate (Q)

The density of dry air can be approximated using the ideal gas law, which states that the density is directly proportional to the pressure and inversely proportional to the temperature. However, for simplicity, we will assume constant density in this calculation.

To calculate the volume flow rate of dry air, we need to know the velocity and the cross-sectional area through which the air is flowing. The volume flow rate (Q) is given by the equation:

Volume Flow Rate (Q) = Velocity (V) x Cross-Sectional Area (A)

Now, let’s break down the steps to calculate the mass flow rate of dry air:

1. Measure the velocity (V) of the air: To determine the velocity, you can use various methods such as an anemometer or a pitot tube. Ensure that the velocity measurement is taken at the same location and under the same conditions as the cross-sectional area measurement.

2. Measure the cross-sectional area (A) through which the air is flowing: This can be done by directly measuring the dimensions of the pipe, nozzle, or orifice through which the air is passing. Alternatively, you can use a flowmeter that provides the cross-sectional area measurement.

3. Calculate the volume flow rate (Q): Multiply the velocity (V) by the cross-sectional area (A) to obtain the volume flow rate (Q).

4. Determine the density (ρ) of dry air: As mentioned earlier, the density of dry air can be approximated using the ideal gas law. However, for simplicity, we will assume a constant density value.

5. Calculate the mass flow rate (ṁ): Multiply the density (ρ) by the volume flow rate (Q) to obtain the mass flow rate (ṁ) of dry air.

To summarize, the mass flow rate of dry air can be calculated by multiplying the density of dry air by the volume flow rate of the air. The volume flow rate is obtained by multiplying the velocity of the air by the cross-sectional area through which it is flowing. By following these steps and using the appropriate units of measurement, you can accurately determine the mass flow rate of dry air for your specific application.

Remember, understanding and calculating the mass flow rate of dry air is essential for various engineering and scientific applications. By following these steps and utilizing the appropriate measurements and equations, you can accurately determine the mass flow rate and ensure the efficiency and effectiveness of your system.

How to Calculate Mass Flow Rate of Steam

To accurately determine the mass flow rate of steam, we need to understand the underlying principles of fluid dynamics and utilize the appropriate equations. Mass flow rate is a crucial parameter in various engineering applications, including thermodynamics, fluid mechanics, and measurement.

Formula for Steam Mass Flow Rate

The mass flow rate of steam can be calculated using the equation:

Mass Flow Rate = Volume Flow Rate × Density

The volume flow rate represents the amount of steam passing through a given point per unit time, while density refers to the mass per unit volume of the steam. By multiplying these two values together, we can obtain the mass flow rate of the steam.

To calculate the volume flow rate, we can use the equation:

Volume Flow Rate = Velocity × Cross-Sectional Area

The velocity represents the speed at which the steam is flowing, while the cross-sectional area refers to the area perpendicular to the direction of flow. By multiplying these two values, we can determine the volume flow rate.

Conservation of Mass

The concept of conservation of mass is fundamental in fluid dynamics. According to this principle, the mass entering a system must equal the mass leaving the system. This principle allows us to calculate the mass flow rate by measuring the volume flow rate and density at a specific point.

Units and Measurement

When calculating the mass flow rate of steam, it is essential to ensure that the units are consistent. The SI unit for mass flow rate is kilograms per second (kg/s), while the unit for volume flow rate is cubic meters per second (m³/s). Density is typically measured in kilograms per cubic meter (kg/m³), and velocity is measured in meters per second (m/s).

To obtain accurate measurements, engineers often use specialized instruments such as flowmeters, nozzles, orifices, and pressure sensors. These devices allow for precise measurement of parameters required to calculate the mass flow rate.

Example Calculation

Let’s consider an example to illustrate the calculation of the mass flow rate of steam. Suppose we have a steam pipe with a velocity of 10 m/s and a cross-sectional area of 0.5 m². The density of the steam is 2 kg/m³.

First, we calculate the volume flow rate:

Volume Flow Rate = Velocity × Cross-Sectional Area
Volume Flow Rate = 10 m/s × 0.5 m²
Volume Flow Rate = 5 m³/s

Next, we calculate the mass flow rate:

Mass Flow Rate = Volume Flow Rate × Density
Mass Flow Rate = 5 m³/s × 2 kg/m³
Mass Flow Rate = 10 kg/s

Therefore, the mass flow rate of steam in this example is 10 kg/s.

In conclusion, calculating the mass flow rate of steam involves understanding the principles of fluid dynamics, utilizing appropriate equations, and ensuring consistent units and measurements. By following these steps, engineers can accurately determine the mass flow rate, a crucial parameter in various engineering applications.

How to Calculate Mass Flow Rate of Water

To understand how to calculate the mass flow rate of water, we first need to grasp the concept of mass flow rate itself. Mass flow rate is a fundamental parameter in fluid dynamics that measures the amount of mass passing through a given point per unit of time. It is an essential quantity in various fields, including engineering, thermodynamics, and fluid mechanics.

Calculation of Mass Flow Rate of Water

The mass flow rate of water can be calculated using a simple equation derived from the principle of conservation of mass. The equation is as follows:

Mass Flow Rate = Density × Volume Flow Rate

To calculate the mass flow rate, we need to determine the density of the water and the volume flow rate.

Determining the Density of Water

The density of water is a well-known value and can be considered constant under normal conditions. At room temperature and atmospheric pressure, the density of water is approximately 1000 kilograms per cubic meter (kg/m³). However, it is important to note that the density of water can vary slightly with temperature and pressure. For most practical purposes, using the average density of 1000 kg/m³ is sufficient.

Measuring the Volume Flow Rate

To calculate the mass flow rate, we also need to determine the volume flow rate of water. The volume flow rate measures the amount of water passing through a given point per unit of time. It is typically expressed in cubic meters per second (m³/s) or liters per second (L/s).

There are various methods to measure the volume flow rate of water, depending on the application and available equipment. Some common techniques include using a flowmeter, a nozzle, an orifice, or a pipe with known dimensions. These devices can provide accurate measurements of the volume flow rate.

Once we have determined the volume flow rate, we can proceed with calculating the mass flow rate of water.

Calculating the Mass Flow Rate

To calculate the mass flow rate, we multiply the density of water by the volume flow rate. Let’s consider an example to illustrate this calculation:

Suppose we have a volume flow rate of 0.5 cubic meters per second (m³/s) of water. Using the average density of water (1000 kg/m³), we can calculate the mass flow rate as follows:

Mass Flow Rate = Density × Volume Flow Rate
= 1000 kg/m³ × 0.5 m³/s
= 500 kg/s

Therefore, the mass flow rate of water in this example is 500 kilograms per second (kg/s).

It is important to note that the units used for the density and volume flow rate must be consistent to obtain accurate results. Additionally, when working with different units, appropriate conversions should be applied to ensure accurate calculations.

In conclusion, calculating the mass flow rate of water involves determining the density of water and the volume flow rate. By multiplying these two values together, we can obtain the mass flow rate. This calculation is crucial in various applications, such as fluid dynamics, engineering, and thermodynamics, where understanding the movement of fluids is essential.

How to Calculate Mass Flow Rate from Enthalpy

In fluid dynamics, calculating the mass flow rate is an essential task that helps engineers and scientists understand the movement of fluids through a system. One way to determine the mass flow rate is by utilizing the concept of enthalpy. Enthalpy is a thermodynamic property that accounts for the internal energy of a fluid, including its heat content and work done. By considering the change in enthalpy across a system, we can calculate the mass flow rate accurately.

Calculation of Mass Flow Rate from Enthalpy

To calculate the mass flow rate from enthalpy, we need to consider the conservation of mass principle. According to this principle, the mass entering a system must equal the mass leaving the system. By applying this principle and utilizing the equation for enthalpy, we can determine the mass flow rate.

The equation for mass flow rate from enthalpy is as follows:

Mass Flow Rate (ṁ) = (Enthalpy Change (ΔH)) / (Specific Enthalpy (h))

Where:
– Mass Flow Rate (ṁ) is the amount of mass passing through a given point per unit time.
– Enthalpy Change (ΔH) is the difference in enthalpy between the inlet and outlet of the system.
– Specific Enthalpy (h) is the enthalpy per unit mass of the fluid.

By rearranging the equation, we can solve for the mass flow rate:

ṁ = ΔH / h

To calculate the mass flow rate, we need to know the enthalpy change and the specific enthalpy of the fluid. The enthalpy change can be determined by measuring the heat transfer or work done on the fluid. The specific enthalpy can be obtained from tables or equations specific to the fluid being analyzed.

It is important to note that the units of the enthalpy change and specific enthalpy must be consistent for accurate calculations. Common units for enthalpy include joules (J) or kilojoules (kJ), while specific enthalpy is typically measured in joules per kilogram (J/kg) or kilojoules per kilogram (kJ/kg).

Example Calculation

Let’s consider an example to illustrate the calculation of mass flow rate from enthalpy. Suppose we have a system where the enthalpy change is 500 kJ and the specific enthalpy is 50 kJ/kg. We can use the equation mentioned earlier to find the mass flow rate:

ṁ = ΔH / h

ṁ = 500 kJ / 50 kJ/kg

ṁ = 10 kg/s

In this example, the mass flow rate is determined to be 10 kilograms per second.

Conclusion

Calculating the mass flow rate from enthalpy is a fundamental concept in fluid dynamics. By considering the conservation of mass principle and utilizing the equation for enthalpy, engineers and scientists can accurately determine the amount of mass passing through a system per unit time. This calculation is crucial for various applications in engineering and thermodynamics, allowing for a better understanding of fluid mechanics and system performance.

How to Calculate Mass Flow Rate from Pressure Drop

In fluid dynamics, calculating the mass flow rate is an essential task in various engineering applications. One common method to determine the mass flow rate is by measuring the pressure drop across a system. By understanding the relationship between pressure drop and mass flow rate, we can gain valuable insights into the behavior of fluids in different scenarios.

Calculation of Mass Flow Rate from Pressure Drop

To calculate the mass flow rate from a pressure drop, we need to consider several factors, including the fluid’s density, velocity, and the cross-sectional area of the flow. The equation we use to calculate the mass flow rate is derived from the principle of conservation of mass.

The equation for mass flow rate is as follows:

Mass Flow Rate = Density * Velocity * Cross-sectional Area

Let’s break down each component of the equation to understand how they contribute to the calculation.

Density

Density is a measure of how much mass is contained within a given volume of a substance. It is usually represented by the Greek letter rho (ρ) and is measured in kilograms per cubic meter (kg/m³). The density of a fluid is influenced by factors such as temperature and pressure.

To calculate the mass flow rate, we need to know the density of the fluid. This information can be obtained from fluid property tables or by using equations specific to the fluid being analyzed.

Velocity

Velocity refers to the speed at which the fluid is flowing through a particular point in the system. It is typically measured in meters per second (m/s). The velocity of the fluid can be determined by measuring the flow rate or by using flow measurement devices such as flowmeters.

Cross-sectional Area

The cross-sectional area is the area perpendicular to the direction of flow. It represents the size of the opening through which the fluid is passing. The cross-sectional area is measured in square meters (m²) and can be calculated using the dimensions of the flow path, such as the diameter of a pipe or the dimensions of a nozzle or orifice.

Putting It All Together

To calculate the mass flow rate from a pressure drop, we need to gather the necessary information: the density of the fluid, the velocity of the flow, and the cross-sectional area of the system. Once we have these values, we can plug them into the equation mentioned earlier:

Mass Flow Rate = Density * Velocity * Cross-sectional Area

By substituting the appropriate units for each variable, we can obtain the mass flow rate in units such as kilograms per second (kg/s) or pounds per hour (lb/hr), depending on the desired measurement.

Example Calculation

Let’s consider an example to illustrate the calculation of mass flow rate from a pressure drop. Suppose we have a pipe with a diameter of 0.5 meters and a fluid flowing through it with a velocity of 2 meters per second. The density of the fluid is 1000 kilograms per cubic meter.

Using the equation mentioned earlier, we can calculate the cross-sectional area of the pipe:

Cross-sectional Area = π * (Diameter/2)^2
= π * (0.5/2)^2
= 0.1963 square meters

Now, we can calculate the mass flow rate:

Mass Flow Rate = Density * Velocity * Cross-sectional Area
= 1000 kg/m³ * 2 m/s * 0.1963 m²
= 392.6 kg/s

Therefore, the mass flow rate through the pipe is 392.6 kilograms per second.

Conclusion

Calculating the mass flow rate from a pressure drop is a fundamental concept in fluid mechanics and engineering. By understanding the relationship between pressure drop, density, velocity, and cross-sectional area, we can accurately determine the mass flow rate of a fluid. This knowledge is crucial in various industries, including manufacturing, energy, and transportation, where the efficient movement of fluids is essential for optimal system performance.

How to Calculate Mass Flow Rate of Fuel in an Engine

Fuel mass flow rate is an important parameter to consider when analyzing the performance of an engine. It helps us understand how much fuel is being consumed and how efficiently it is being utilized. By calculating the mass flow rate of fuel, we can gain insights into the engine’s efficiency and make informed decisions regarding its operation and optimization.

Calculation of Fuel Mass Flow Rate in an Engine

To calculate the mass flow rate of fuel in an engine, we need to consider several factors, including the volume flow rate, density, and velocity of the fuel. The equation used to calculate the mass flow rate is derived from the principle of conservation of mass.

1. Determine the Volume Flow Rate: The volume flow rate represents the amount of fuel passing through a specific point in the engine per unit time. It is typically measured in liters per second (L/s) or cubic meters per second (m³/s). To calculate the volume flow rate, we need to know the cross-sectional area of the flow path and the velocity of the fuel.

2. Measure the Cross-Sectional Area: The cross-sectional area refers to the area perpendicular to the direction of flow. It can be determined by measuring the dimensions of the flow path, such as the diameter of a pipe or the area of an orifice. Ensure that the units of the cross-sectional area are consistent with the units used for the velocity and density.

3. Determine the Velocity of the Fuel: The velocity of the fuel represents the speed at which it flows through the engine. It can be measured using various techniques, such as flowmeters or by calculating it based on the pressure drop across a nozzle. Ensure that the units of velocity are consistent with the units used for the cross-sectional area and density.

4. Calculate the Density of the Fuel: The density of the fuel is a measure of its mass per unit volume. It can vary depending on the type of fuel being used. The density is typically provided by fuel manufacturers and can be expressed in kilograms per cubic meter (kg/m³) or grams per cubic centimeter (g/cm³).

5. Apply the Mass Flow Rate Equation: Once we have obtained the volume flow rate, density, and velocity of the fuel, we can calculate the mass flow rate using the equation:

Mass Flow Rate = Volume Flow Rate × Density

Ensure that the units of the mass flow rate are consistent with the units used for the volume flow rate and density. It is also important to note that the mass flow rate can be positive or negative, depending on the direction of flow.

By following these steps and accurately measuring the necessary parameters, we can calculate the mass flow rate of fuel in an engine. This information can be used to monitor fuel consumption, optimize engine performance, and make informed decisions regarding fuel efficiency. Understanding the mass flow rate is crucial for engineers and technicians working in the field of thermodynamics, fluid mechanics, and engineering.

How to Calculate Mass Flow Rate in Ansys Fluent

Introduction to Ansys Fluent

Ansys Fluent is a powerful computational fluid dynamics (CFD) software widely used in engineering and scientific applications. It allows engineers and researchers to simulate and analyze fluid flow, heat transfer, and other related phenomena. One important parameter in fluid dynamics is the mass flow rate, which measures the amount of mass passing through a given point per unit time. Calculating the mass flow rate accurately is crucial for understanding and optimizing various processes involving fluids.

Calculation of Mass Flow Rate in Ansys Fluent

To calculate the mass flow rate in Ansys Fluent, we need to consider the fundamental principle of conservation of mass. According to this principle, the mass entering a control volume must be equal to the mass leaving it, assuming no mass is being generated or consumed within the volume.

To calculate the mass flow rate, we can use the equation:

Mass Flow Rate = Density × Velocity × Cross-sectional Area

Let’s break down each component of this equation:

1. Density: Density is a measure of how much mass is contained within a given volume of a substance. It is typically denoted by the symbol ρ and is expressed in units such as kg/m³ or g/cm³. In Ansys Fluent, the density of the fluid can be specified based on the properties of the material being simulated.

2. Velocity: Velocity refers to the speed at which the fluid is flowing. It is denoted by the symbol v and is typically measured in units of meters per second (m/s) or feet per second (ft/s). In Ansys Fluent, the velocity can be obtained from the simulation results or specified as an input parameter.

3. Cross-sectional Area: The cross-sectional area represents the area perpendicular to the flow direction. It is denoted by the symbol A and is typically measured in square meters (m²) or square feet (ft²). The cross-sectional area depends on the geometry of the system under consideration, such as the shape of a pipe, nozzle, orifice, or flowmeter.

By multiplying the density, velocity, and cross-sectional area, we can determine the mass flow rate. It is important to ensure that the units of each component are consistent to obtain accurate results.

Example Calculation

Let’s consider a simple example to illustrate the calculation of mass flow rate in Ansys Fluent. Suppose we have a pipe with a diameter of 0.1 meters and water flowing through it at a velocity of 2 meters per second. The density of water is approximately 1000 kg/m³.

To calculate the mass flow rate, we first need to determine the cross-sectional area of the pipe. The cross-sectional area of a pipe can be calculated using the formula:

Cross-sectional Area = π × (Diameter/2)²

Substituting the values into the equation:

Cross-sectional Area = π × (0.1/2)² = 0.00785 m²

Next, we multiply the density, velocity, and cross-sectional area:

Mass Flow Rate = 1000 kg/m³ × 2 m/s × 0.00785 m² = 15.7 kg/s

Therefore, the mass flow rate of water through the pipe is 15.7 kilograms per second.

Conclusion

Calculating the mass flow rate in Ansys Fluent is essential for understanding and analyzing fluid dynamics in various engineering and scientific applications. By considering the principles of conservation of mass and using the equation involving density, velocity, and cross-sectional area, engineers and researchers can accurately determine the mass flow rate. This information is crucial for designing and optimizing systems involving fluid flow, such as pipes, nozzles, orifices, and flowmeters.

Frequently Asked Questions

How to calculate mass flow rate in a heat exchanger?

To calculate the mass flow rate in a heat exchanger, you can use the equation:

[ text{Mass Flow Rate} = text{Volume Flow Rate} times text{Density} ]

How to calculate mass flow rate in Paraview?

Paraview is a visualization software and does not directly calculate mass flow rate. However, you can export the data from Paraview and use other tools or equations to calculate the mass flow rate.

How to calculate mass flow rate of a compressor?

To calculate the mass flow rate of a compressor, you can use the equation:

[ text{Mass Flow Rate} = text{Volume Flow Rate} times text{Density} ]

How to find mass flow rate in thermodynamics?

In thermodynamics, you can find the mass flow rate by using the equation:

[ text{Mass Flow Rate} = text{Volume Flow Rate} times text{Density} ]

How to calculate mass flow rate of exhaust gas?

To calculate the mass flow rate of exhaust gas, you can use the equation:

[ text{Mass Flow Rate} = text{Volume Flow Rate} times text{Density} ]

How to calculate mass flow rate of gas?

To calculate the mass flow rate of a gas, you can use the equation:

[ text{Mass Flow Rate} = text{Volume Flow Rate} times text{Density} ]

How to calculate mass flow rate from density?

To calculate the mass flow rate from density, you can use the equation:

[ text{Mass Flow Rate} = text{Volume Flow Rate} times text{Density} ]

How to calculate mass flow rate of air?

To calculate the mass flow rate of air, you can use the equation:

[ text{Mass Flow Rate} = text{Volume Flow Rate} times text{Density} ]

How to calculate mass flow rate of refrigerant?

To calculate the mass flow rate of a refrigerant, you can use the equation:

[ text{Mass Flow Rate} = text{Volume Flow Rate} times text{Density} ]

How to calculate mass flow rate of dry air?

To calculate the mass flow rate of dry air, you can use the equation:

[ text{Mass Flow Rate} = text{Volume Flow Rate} times text{Density} ]

How to calculate mass flow rate of steam?

To calculate the mass flow rate of steam, you can use the equation:

[ text{Mass Flow Rate} = text{Volume Flow Rate} times text{Density} ]

How to calculate mass flow rate of water?

To calculate the mass flow rate of water, you can use the equation:

[ text{Mass Flow Rate} = text{Volume Flow Rate} times text{Density} ]

How to calculate mass flow rate from enthalpy?

To calculate the mass flow rate from enthalpy, you can use the equation:

[ text{Mass Flow Rate} = frac{text{Heat Transfer Rate}}{text{Enthalpy Difference}} ]

How to calculate mass flow rate from pressure drop?

To calculate the mass flow rate from pressure drop, you can use the equation:

[ text{Mass Flow Rate} = frac{text{Pressure Drop}}{text{Resistance}} ]

How to calculate mass flow rate of fuel in an engine?

To calculate the mass flow rate of fuel in an engine, you can use the equation:

[ text{Mass Flow Rate} = text{Fuel Flow Rate} times text{Density} ]

How to calculate mass flow rate?

To calculate the mass flow rate, you can use the equation:

[ text{Mass Flow Rate} = text{Volume Flow Rate} times text{Density} ]

How to calculate mass flow rate in ANSYS Fluent?

In ANSYS Fluent, you can calculate the mass flow rate by post-processing the simulation results. The software provides tools to extract the mass flow rate from the simulation domain.

Specific Enthalpy vs Enthalpy

Enthalpy is a fundamental concept in thermodynamics that measures the total heat content of a system. It is often used to describe the energy changes that occur during chemical reactions or phase transitions. However, there is another term closely related to enthalpy known as specific enthalpy. While both terms are used to quantify energy changes, they have distinct differences in their definitions and applications. In this article, we will explore the differences between specific enthalpy and enthalpy, and understand how they are used in various fields of science and engineering. So, let’s dive in and unravel the mysteries behind these two important concepts in thermodynamics.

Key Takeaways

• Enthalpy is a thermodynamic property that represents the total heat content of a system, while specific enthalpy is the enthalpy per unit mass of a substance.
• Specific enthalpy is useful in engineering applications as it allows for more accurate calculations and comparisons between different substances.
• Enthalpy is typically measured in units of energy, such as joules or calories, while specific enthalpy is measured in units of energy per unit mass, such as joules per kilogram.
• The specific enthalpy of a substance can be calculated by dividing the enthalpy by the mass of the substance.
• Both enthalpy and specific enthalpy are important concepts in thermodynamics and are used to analyze and design various processes and systems.

Enthalpy vs Specific Enthalpy

Enthalpy: Definition and Components (Internal Energy and Pressure-Volume Work)

Enthalpy is a fundamental concept in thermodynamics that helps us understand the energy content of a system. It is denoted by the symbol “H” and is defined as the sum of the internal energy (U) and the product of pressure (P) and volume (V) of the system. In other words, enthalpy accounts for both the heat energy and the work done by the system.

The internal energy represents the total energy stored within the system, including the kinetic and potential energies of its particles. On the other hand, the pressure-volume work accounts for the energy transferred to or from the system due to changes in its volume under constant pressure.

Specific Enthalpy: Definition as Enthalpy per Unit Mass

Specific enthalpy, denoted as “h,” is the enthalpy per unit mass of a substance. It is obtained by dividing the enthalpy (H) of the system by its mass (m). Specific enthalpy allows us to analyze the energy content of a substance on a per-unit-mass basis, which is particularly useful in engineering and thermodynamic calculations.

By expressing enthalpy in terms of mass, specific enthalpy enables us to compare the energy content of different substances or different amounts of the same substance.

Comparison between Enthalpy and Specific Enthalpy

The main difference between enthalpy and specific enthalpy lies in their units and the way they are used. Enthalpy is an extensive property, meaning it depends on the size or amount of the system. On the other hand, specific enthalpy is an intensive property, which remains constant regardless of the system size.

Enthalpy allows us to analyze the total energy content of a system, taking into account both the internal energy and the work done. It is commonly used in thermodynamic calculations, such as determining the heat transfer in chemical reactions or phase changes.

Specific enthalpy, on the other hand, provides a more detailed analysis by considering the energy content on a per-unit-mass basis. It is particularly useful in engineering applications, such as calculating the energy required for heating or cooling a specific mass of a substance.

Units of Measurement for Enthalpy and Specific Enthalpy

Enthalpy is typically measured in units of energy, such as joules (J) or calories (cal). The SI unit for enthalpy is joule, while the calorie is commonly used in the field of chemistry.

Specific enthalpy is expressed in the same units as enthalpy but divided by mass. Therefore, the units for specific enthalpy are joules per kilogram (J/kg) or calories per gram (cal/g).

To summarize, enthalpy and specific enthalpy are both important concepts in thermodynamics. Enthalpy provides a comprehensive analysis of the energy content of a system, while specific enthalpy allows for a more detailed examination on a per-unit-mass basis. Understanding these concepts is crucial for engineers, scientists, and anyone working with energy systems.

Specific Enthalpy of Steam Water System

The specific enthalpy of a steam water system is a crucial thermodynamic property that helps us understand the energy content of the system. It is defined as the amount of heat energy per unit mass of a substance, and it plays a significant role in various engineering applications, particularly in the field of thermodynamics.

Specific Enthalpy Values for Vaporization and Saturation of Water

When water undergoes a phase change from a liquid to a vapor state, it requires a certain amount of energy. This energy is known as the specific enthalpy of vaporization. It represents the heat energy needed to convert one unit mass of liquid water into vapor at a given temperature and pressure.

Similarly, the specific enthalpy of saturation refers to the energy content of water when it exists in a saturated state. In this state, water is at the boiling point corresponding to a specific pressure. The specific enthalpy of saturation is the sum of the specific enthalpy of liquid water and the specific enthalpy of vaporization.

Calculation of Specific Enthalpy for Saturated Steam at Atmospheric Pressure

To calculate the specific enthalpy for saturated steam at atmospheric pressure, we need to consider the specific enthalpy of liquid water and the specific enthalpy of vaporization. The specific enthalpy of liquid water can be determined using tables or equations based on temperature. The specific enthalpy of vaporization can also be obtained from tables or correlations.

By adding the specific enthalpy of liquid water and the specific enthalpy of vaporization, we can determine the specific enthalpy of saturated steam at atmospheric pressure. This value represents the energy content of steam in its saturated state.

Increase in Specific Enthalpy with System Pressure

As the pressure of a steam water system increases, the specific enthalpy also increases. This is because higher pressures require more energy to convert water into steam. The specific enthalpy of steam at a given pressure is higher than that at atmospheric pressure due to the additional energy required for vaporization.

The increase in specific enthalpy with system pressure is an important consideration in various industrial processes, such as power generation and steam-driven machinery. Understanding the relationship between pressure and specific enthalpy allows engineers to design efficient systems and optimize energy usage.

Calculation of Specific Enthalpy for Superheated Steam

Superheated steam refers to steam that has been heated beyond its saturation point. To calculate the specific enthalpy for superheated steam, we need to consider the specific enthalpy of saturated steam and the specific enthalpy of superheating.

The specific enthalpy of saturated steam can be determined as mentioned earlier. The specific enthalpy of superheating represents the additional energy required to heat the steam beyond its saturation point. This value can be obtained from tables or correlations based on the temperature and pressure of the superheated steam.

By adding the specific enthalpy of saturated steam and the specific enthalpy of superheating, we can determine the specific enthalpy of superheated steam. This value represents the total energy content of steam in its superheated state.

Molar Enthalpy vs Specific Enthalpy

Definition of Molar Enthalpy and Specific Enthalpy

Enthalpy is a fundamental concept in thermodynamics that measures the total energy of a system. It is denoted by the symbol “H” and is often used to describe heat transfer and energy changes in chemical reactions. Molar enthalpy and specific enthalpy are two related but distinct concepts that are commonly used in different contexts.

Molar enthalpy, also known as molar heat capacity, is the amount of heat required to raise the temperature of one mole of a substance by one degree Celsius. It is represented by the symbol “Cp” and has units of joules per mole per degree Celsius (J/mol·°C). Molar enthalpy takes into account the mass of the substance and is used to calculate the enthalpy change in reactions.

On the other hand, specific enthalpy, also known as specific heat capacity, is the amount of heat required to raise the temperature of a unit mass of a substance by one degree Celsius. It is represented by the symbol “cp” and has units of joules per kilogram per degree Celsius (J/kg·°C). Specific enthalpy is used for heat balance calculations in engineering and is independent of the mass of the substance.

Differences between Molar Enthalpy and Specific Enthalpy

The main difference between molar enthalpy and specific enthalpy lies in the units of measurement and the quantity being considered. Molar enthalpy is expressed in terms of moles of a substance, while specific enthalpy is expressed in terms of kilograms of a substance.

Molar enthalpy takes into account the mass of the substance and is used to calculate the enthalpy change in reactions. It is particularly useful in chemical reactions where the quantities involved are often measured in moles. Specific enthalpy, on the other hand, is used for heat balance calculations in engineering, where the focus is on the energy required to heat or cool a given mass of a substance.

Molar Enthalpy used for calculating enthalpy change in reactions

Molar enthalpy is commonly used in chemical reactions to calculate the enthalpy change, also known as the heat of reaction. The enthalpy change is the difference in enthalpy between the products and the reactants in a chemical reaction. By knowing the molar enthalpies of the reactants and products, it is possible to calculate the enthalpy change using the principle of conservation of energy.

For example, in the combustion of methane (CH4), the molar enthalpy of methane is -890.3 kJ/mol, and the molar enthalpy of carbon dioxide (CO2) is -393.5 kJ/mol. By subtracting the molar enthalpy of the reactants from the molar enthalpy of the products, the enthalpy change of the reaction can be determined.

Specific Enthalpy used for heat balance calculations in engineering

Specific enthalpy is widely used in engineering for heat balance calculations. Heat balance calculations involve determining the amount of heat energy required to heat or cool a given mass of a substance. Specific enthalpy allows engineers to calculate the energy requirements for various processes, such as heating water or cooling air.

For example, in HVAC (Heating, Ventilation, and Air Conditioning) systems, specific enthalpy is used to calculate the energy required to heat or cool air as it flows through the system. By knowing the specific enthalpy of the incoming and outgoing air, engineers can determine the amount of energy needed to achieve the desired temperature change.

Units of measurement for Molar Enthalpy and Specific Enthalpy

Molar enthalpy is measured in joules per mole per degree Celsius (J/mol·°C), while specific enthalpy is measured in joules per kilogram per degree Celsius (J/kg·°C). These units reflect the different quantities being considered – moles for molar enthalpy and kilograms for specific enthalpy.

Calculation of total enthalpy change using Molar Enthalpy and Specific Enthalpy

To calculate the total enthalpy change in a system, both molar enthalpy and specific enthalpy can be used. The molar enthalpy is used to determine the enthalpy change at the molecular level, while the specific enthalpy is used to determine the enthalpy change at the mass level.

The total enthalpy change can be calculated by multiplying the molar enthalpy by the number of moles involved in the reaction and adding it to the product of the specific enthalpy and the mass of the substance. This allows for a comprehensive understanding of the energy changes occurring in a system.

Different Types of Enthalpy Change

Enthalpy change refers to the amount of heat energy transferred during a chemical reaction or physical process. There are various types of enthalpy changes that occur in different scenarios. Let’s explore some of the most common types of enthalpy changes.

Explanation of Various Types of Enthalpy Changes

1. Enthalpy of Reaction: The enthalpy change associated with a chemical reaction is known as the enthalpy of reaction. It represents the difference in enthalpy between the products and the reactants. This value can be positive or negative, depending on whether the reaction is exothermic (releases heat) or endothermic (absorbs heat).

2. Enthalpy of Combustion: The enthalpy change that occurs during the combustion of a substance is called the enthalpy of combustion. It measures the heat energy released when a substance reacts with oxygen to form carbon dioxide and water.

3. Enthalpy of Formation: The enthalpy change when one mole of a compound is formed from its constituent elements in their standard states is known as the enthalpy of formation. It provides information about the stability and energy content of the compound.

4. Enthalpy of Neutralization: The enthalpy change that occurs when an acid reacts with a base to form a salt and water is called the enthalpy of neutralization. It represents the heat energy released or absorbed during the neutralization process.

5. Enthalpy of Solution: The enthalpy change associated with the dissolution of a solute in a solvent is known as the enthalpy of solution. It measures the heat energy released or absorbed when a solute dissolves to form a solution.

6. Enthalpy of Fusion: The enthalpy change when a substance changes from a solid to a liquid state at its melting point is called the enthalpy of fusion. It represents the heat energy required to overcome the intermolecular forces holding the solid together.

7. Enthalpy of Sublimation: The enthalpy change when a substance changes directly from a solid to a gaseous state without passing through the liquid state is known as the enthalpy of sublimation. It measures the heat energy required to overcome the forces holding the solid together and convert it into a gas.

8. Enthalpy of Vaporization: The enthalpy change when a substance changes from a liquid to a gaseous state at its boiling point is called the enthalpy of vaporization. It represents the heat energy required to overcome the intermolecular forces holding the liquid together.

9. Enthalpy of Mixing: The enthalpy change that occurs when two or more substances are mixed together is known as the enthalpy of mixing. It measures the heat energy released or absorbed during the mixing process.

By understanding these different types of enthalpy changes, we can gain insights into the energy transformations that occur during chemical reactions and physical processes. These values play a crucial role in various scientific and engineering applications, such as designing efficient energy systems and understanding the thermodynamics of chemical reactions.

Favorable Enthalpy

Enthalpy is a fundamental concept in thermodynamics that helps us understand the energy changes that occur during chemical reactions. It plays a crucial role in determining whether a reaction is favorable or not. In this section, we will explore the relationship between enthalpy change and reaction favorability, as well as introduce the concept of Gibbs free energy.

Favorability of a reaction based on enthalpy change

The enthalpy change of a reaction, often denoted as ΔH, is a measure of the heat energy absorbed or released during a chemical reaction. It represents the difference in enthalpy between the products and the reactants. By analyzing the sign and magnitude of ΔH, we can determine whether a reaction is exothermic or endothermic.

An exothermic reaction releases heat energy to the surroundings, resulting in a negative ΔH value. On the other hand, an endothermic reaction absorbs heat energy from the surroundings, leading to a positive ΔH value. The magnitude of ΔH indicates the amount of heat energy involved in the reaction.

Relationship between enthalpy change and entropy change

Entropy, denoted as ΔS, is a measure of the disorder or randomness in a system. It accounts for the number of ways in which the particles of a system can be arranged. A positive ΔS value indicates an increase in disorder, while a negative ΔS value suggests a decrease in disorder.

The relationship between enthalpy change (ΔH) and entropy change (ΔS) is described by the equation:

ΔG = ΔH – TΔS

where ΔG is the Gibbs free energy change and T is the temperature in Kelvin. The Gibbs free energy change determines the spontaneity of a reaction. If ΔG is negative, the reaction is spontaneous and favorable. If ΔG is positive, the reaction is non-spontaneous and unfavorable. If ΔG is zero, the reaction is at equilibrium.

Gibbs free energy (ΔG) is a thermodynamic potential that combines the effects of enthalpy change (ΔH) and entropy change (ΔS) to determine the spontaneity of a reaction. It provides a more comprehensive understanding of reaction favorability compared to enthalpy alone.

The equation ΔG = ΔH – TΔS tells us that for a reaction to be favorable, the enthalpy change must be negative (exothermic) and the entropy change must be positive (increase in disorder). However, the temperature also plays a crucial role. At low temperatures, a negative enthalpy change dominates, making the reaction favorable. At high temperatures, a positive entropy change dominates, making the reaction favorable.

Frequently Asked Questions

1. Why are enthalpy values different?

Enthalpy values can vary depending on the specific process or reaction being considered. Factors such as temperature, pressure, and the presence of other substances can influence the enthalpy of a system, leading to differences in the measured values.

2. Is enthalpy the same as specific heat?

No, enthalpy and specific heat are different properties. Enthalpy is a measure of the total energy of a system, including both its internal energy and the work done on or by the system. Specific heat, on the other hand, is a measure of the amount of heat required to raise the temperature of a unit mass of a substance by a certain amount.

3. What is the difference between specific heat capacity and enthalpy?

Specific heat capacity refers to the amount of heat required to raise the temperature of a unit mass of a substance by a certain amount. Enthalpy, on the other hand, is a measure of the total energy of a system, including both its internal energy and the work done on or by the system. While specific heat capacity is a property of a substance, enthalpy is a property of a system.

4. Why is the experimental enthalpy higher than the theoretical value?

There can be several reasons for the experimental enthalpy to be higher than the theoretical value. Experimental errors, incomplete reactions, side reactions, and impurities in the reactants can all contribute to the deviation between the experimental and theoretical enthalpy values.

5. What is the difference between standard enthalpy and enthalpy?

Standard enthalpy refers to the enthalpy change that occurs under standard conditions, which typically include a temperature of 25°C and a pressure of 1 bar. Enthalpy, on the other hand, is a more general term that refers to the total energy of a system, including both its internal energy and the work done on or by the system.

6. What is specific enthalpy?

Specific enthalpy is the enthalpy per unit mass of a substance. It is a measure of the total energy of a unit mass of a substance, including both its internal energy and the work done on or by the substance.

7. What is the difference between enthalpy change and standard enthalpy change?

Enthalpy change refers to the difference in enthalpy between the reactants and the products in a chemical reaction. It can be positive (endothermic) or negative (exothermic). Standard enthalpy change, on the other hand, refers to the enthalpy change that occurs under standard conditions, typically at a temperature of 25°C and a pressure of 1 bar.

8. What is the difference between specific enthalpy and enthalpy?

Specific enthalpy refers to the enthalpy per unit mass of a substance, while enthalpy is a more general term that refers to the total energy of a system. Specific enthalpy takes into account the mass of the substance, whereas enthalpy does not.

9. What is the difference between enthalpy of formation and enthalpy of reaction?

Enthalpy of formation refers to the enthalpy change that occurs when one mole of a compound is formed from its constituent elements in their standard states. Enthalpy of reaction, on the other hand, refers to the enthalpy change that occurs in a chemical reaction, regardless of the formation of new compounds.

10. What is the difference between enthalpy of mixing and enthalpy of solution?

Enthalpy of mixing refers to the enthalpy change that occurs when two or more substances are combined to form a mixture. Enthalpy of solution, on the other hand, refers to the enthalpy change that occurs when a solute is dissolved in a solvent to form a solution.

Equivalent Von Mises Stress are generally applied to determine yielding of ductile materials.

Equivalent Von Mises Stress is used to forecast yielding of material when multi axial loads are applied on the body with the help of the results obtained from simple uni-axial tensile tests.

In the above, “equivalent” refers to the combined 3 x 3 stress and it is equivalent to the state of simple tension in such a manner that the magnitude of the stress system can be derived using the data obtained from material’s tensile test.

Von Mises is one of the most commonly referred Equivalent stresses used in material science to estimate and materials strength and durability.

The Von Mises relationship is most widely used by engineers and it has a great importance in data treatment and continuum calculations.

Von Mises stress can be calculated from both individual stress components as well as from the principal stress. The depiction of Von Mises stress through principal stress is much more easier to visualise and hence more commonly used for stress calculation. In terms of principal stress, the Von Mises stress is characterised by equal difference between individual components.

The Von mises stress can be best depicted by the stresses a cube experiences when thrown into a deep sea.

In the above example, the principal stresses that the cube experiences are the buoyancy forces which are equal on all sides with minimal variation based on the difference of the area of each surface. The value of stress would depend only upon the hydrostatic head which increases with the depth of the sea as the cube continues to sink. Since the individual stress components on all sides remain more or less same, the difference between them remains same.

What is Equivalent Von Mises Stress?

Equivalent stress allows one to view stress acting on a structure by one plot. Von Mises equivalent stress is one of the most widely used.

Equivalent Von Mises stress predicts the yielding of materials under a condition of multiaxial loading with the help of the results from simple uniaxial tensile tests. It is indicated by σ_v.

Von Mises stress is a most widely used equivalent stress can be represented as

In terms of stress components

In terms of principal stresses

Both the expression give the same equivalent stress value for same stress state. Von Mises stress is only dependent on the difference between the three principal stresses, therefore it is a good equivalent stress to represent the distortion of a material.

In the principal coordinate system we can plot the expression with principal components as below

Equivalent Von Mises Stress Formula

To verify the point at which a mechanical design has started yielding, a metric of calculation known as Von Mises stress is applied.

The stresses determined at any point of a mechanical structure can be expressed mathematically in terms of a scalar quantity known as Von Mises stress which can be varified with experimentally determined yield points.

The Von Mises relationship for equivalent stress is represented by

The stress components in the above equation are principal stresses. Equivalent stress is obtained with these principal stresses. In case of biaxial stresses σ₃₌ 0 and the equation is reduced to

Using rectangular coordinate system, we get the equations as below:

And

What is Von Mises Equivalent Strain?

In classical mechanics just like Equivalent Von Mises Stress result , Equivalent Von Mises strain is also available.

The equivalent Von Mises strain is given by

The strain elements in the above equation are principal strains and can be obtained from principal stress values.

In rectangular coordinate system,

How do you calculate Von Mises stress in 2D?

Von Mises stress is an evaluation of all the stresses acting on a mechanical structure taking into account normal stresses in both the directions(x and y)and the shear stress.

Von Mises stress in terms of principal stress can be represented by

The strain energy density experienced at a point of a material can be expressed in terms of principal stresses as given below:

The strain energy density experienced at a point in a material can be classified as bellow:

• Dilatational strain energy density, U_h, associated with change in volume
• Distortion strain energy density, U_d, associated with change in shape.

By substracting U_h i.e Dilatational Strain energy density from U₀ i.e total energy density we will get Distortion strain energy(U_d) part.

U_d in terms of equivalent Von Mises stress σ_VM can be written as

In the above formula, Ud is the distortion energy density and when it reaches a critical value, the yielding of ductile material begins. This idea is given by Von Mises theory.

Since this is generally applicable for an uniaxial stress state, we can easily calculate this critical value of distortional energy from uniaxial test.

Here,

 σ1 = σY and σ2 = σ3 = 0.

Where,

σ1, σ2, σ3 are principal stresses, σY is the Yield Stress

The energy density associated with yielding is given by

Replacing Von Misses stress in equation A with principal stress, we obtain equation B. The energy density obtained in equation B is the critical value of the distortional energy density for the material.

As per the Von Mises’s failure criterion, When a material is subjected to multiaxial loading, yielding of the material takes place when the distortional energy = or > than the critical value for the material

Therefore, the yielding of a material starts when the Von Mises stresses acting on the material are greater than the yield stress experienced by the material in a uniaxial tensile test.

In terms of stress components Von Mises stress can be written as

For 2D plane stress state σ3=0, the Von Mises stress in terms of principal stress can be expressed as follows

In terms of general stress components,

How do you calculate Von Mises stress 3D?

Von Mises stress can be expressed in six stress components as follows: