Rabiya Khalid

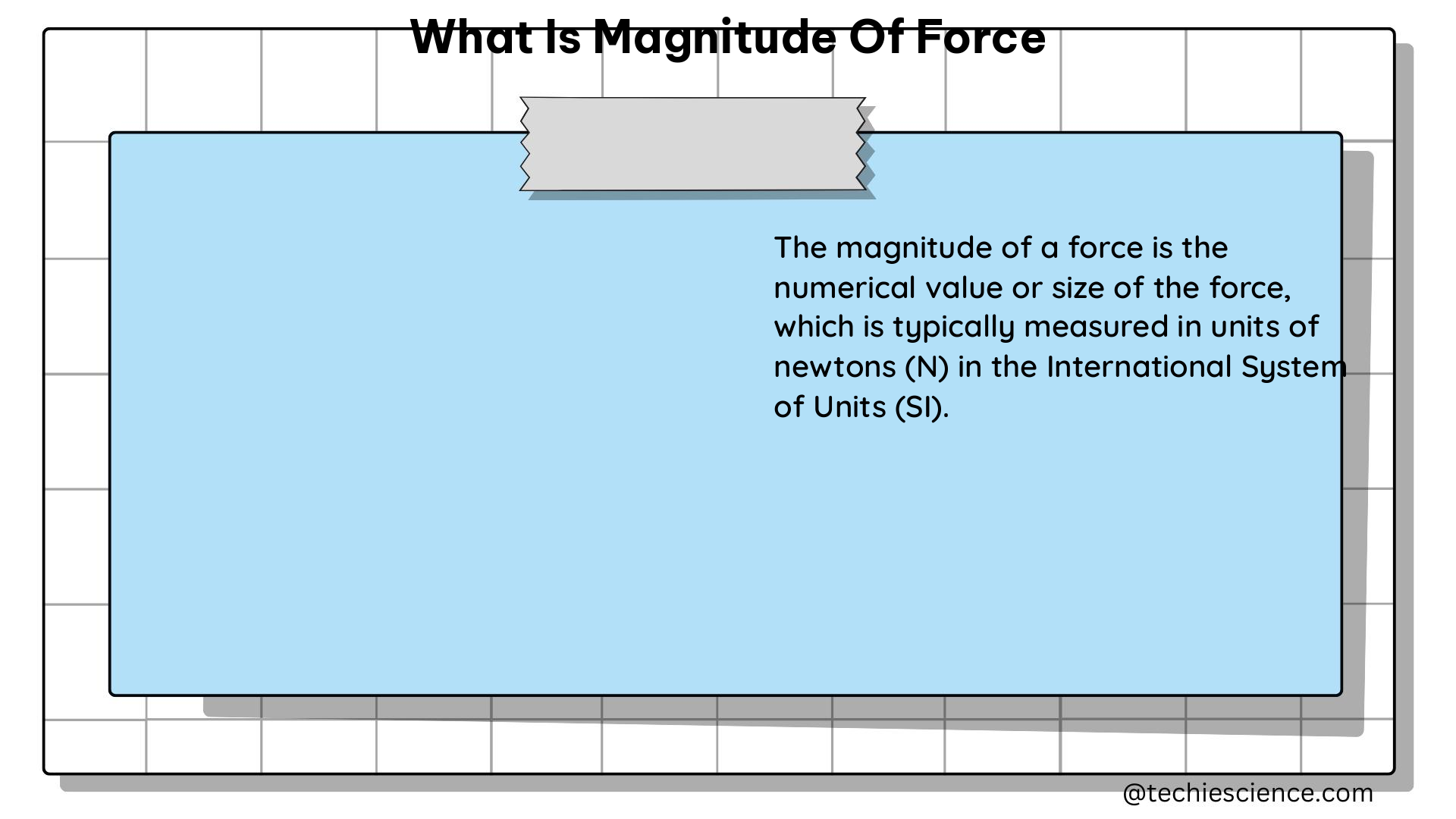
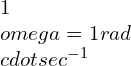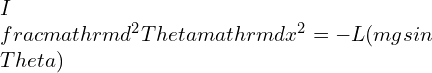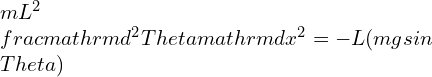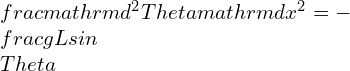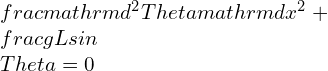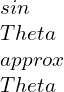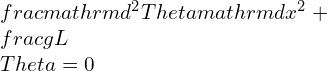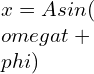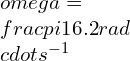Linear frequency is a fundamental concept in the field of signal processing and wave analysis. It plays a crucial role in understanding periodic motion and its relationship to simple harmonic motion. In this section, we will delve into the definition and explanation of periodic motion, as well as explore the connection between simple harmonic motion and periodic motion.

Definition and Explanation of Periodic Motion

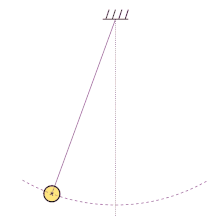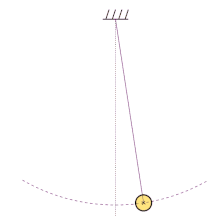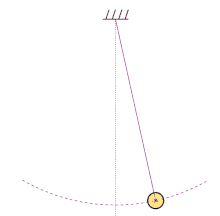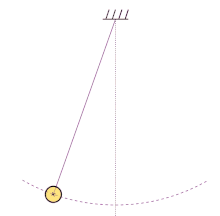
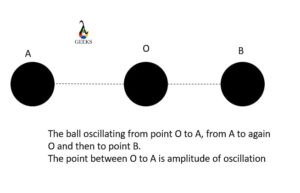
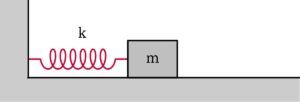
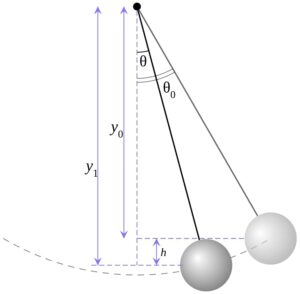
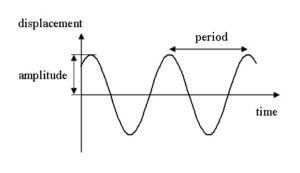
Periodic motion refers to any motion that repeats itself after a certain interval of time. It is characterized by a regular pattern and can be observed in various natural phenomena, such as the swinging of a pendulum, the oscillation of a spring, or the rotation of celestial bodies.

One key aspect of periodic motion is its frequency, which represents the number of complete cycles or oscillations that occur in a given time period. Frequency is typically measured in hertz (Hz), where 1 Hz corresponds to one cycle per second. The linear frequency of a periodic motion refers to the frequency at which the motion occurs in a linear fashion, without any deviation or nonlinearity.

Linear frequency is essential in analyzing and understanding the behavior of periodic systems. By studying the linear frequency of a system, we can gain insights into its dynamics, stability, and response characteristics.

Relationship between Simple Harmonic Motion and Periodic Motion

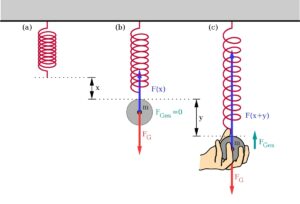
Simple harmonic motion (SHM) is a special type of periodic motion that follows a sinusoidal pattern. It occurs when a restoring force is proportional to the displacement from an equilibrium position. Examples of simple harmonic motion include the back-and-forth motion of a mass-spring system or the oscillation of a pendulum.

The relationship between simple harmonic motion and periodic motion lies in the fact that simple harmonic motion is a specific form of periodic motion. While all simple harmonic motion is periodic, not all periodic motion is necessarily simple harmonic.

In simple harmonic motion, the linear frequency is directly related to the physical properties of the system, such as the mass and spring constant in a mass-spring system or the length and gravitational acceleration in a pendulum. The linear frequency determines the rate at which the system oscillates and is independent of the amplitude of the motion.

Understanding the relationship between simple harmonic motion and periodic motion allows us to analyze and predict the behavior of various systems in fields such as physics, engineering, and even music.

To summarize, linear frequency is a fundamental concept in the study of periodic motion. By examining the linear frequency of a system, we can gain valuable insights into its behavior and response characteristics. Additionally, understanding the relationship between simple harmonic motion and periodic motion helps us analyze and predict the dynamics of various systems. In the following sections, we will explore different aspects of linear frequency and its applications in more detail.

Linear Frequency and its Calculation

Definition of Linear Frequency

Linear frequency refers to the rate at which a wave oscillates or repeats in a linear fashion. It is a fundamental concept in physics and engineering, particularly in the study of waves and vibrations. The linear frequency of a wave is measured in hertz (Hz) and represents the number of complete cycles or oscillations that occur in one second.

Linear frequency can be understood as the inverse of the time period of a wave. It provides information about the speed at which the wave is oscillating or vibrating. The higher the linear frequency, the faster the wave is oscillating, and vice versa.

Calculation of Linear Frequency using Time Period

The linear frequency of a wave can be calculated using its time period. The time period of a wave is the time it takes for one complete cycle or oscillation to occur. It is denoted by the symbol T and is measured in seconds (s).

To calculate the linear frequency using the time period, we can use the formula:

Linear Frequency (f) = 1 / Time Period (T)

For example, if a wave has a time period of 0.02 seconds, we can calculate its linear frequency as:

Linear Frequency (f) = 1 / 0.02 = 50 Hz

This means that the wave completes 50 cycles or oscillations in one second.

Calculation of Linear Frequency using Wave Equation

Another way to calculate the linear frequency of a wave is by using the wave equation. The wave equation relates the linear frequency, wavelength, and the speed of the wave. It is given by the formula:

Linear Frequency (f) = Speed of the Wave (v) / Wavelength (λ)

The speed of the wave represents how fast the wave is propagating through a medium and is measured in meters per second (m/s). The wavelength of a wave is the distance between two consecutive points in a wave that are in phase with each other and is measured in meters (m).

By knowing the speed of the wave and the wavelength, we can calculate the linear frequency using the wave equation.

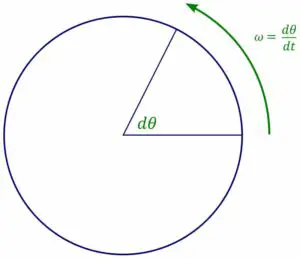
Relation between Linear Frequency and Angular Frequency

Linear frequency and angular frequency are two related concepts in wave analysis. Angular frequency, denoted by the symbol ω (omega), represents the rate at which the phase of a wave changes. It is measured in radians per second (rad/s).

The relationship between linear frequency (f) and angular frequency (ω) is given by the formula:

Angular Frequency (ω) = 2π × Linear Frequency (f)

Here, 2π represents a full cycle or 360 degrees in radians. By multiplying the linear frequency by 2π, we can obtain the angular frequency of a wave.

Units and Symbol of Linear Frequency

Linear frequency is a fundamental concept in the field of signal processing and engineering. It refers to the rate at which a signal or waveform repeats itself in a linear manner. In this section, we will discuss the units used to measure linear frequency and the symbols commonly employed to represent it.

Units of Linear Frequency

The most commonly used unit to measure linear frequency is the Hertz (Hz). One Hertz represents one cycle per second. It is named after Heinrich Hertz, a German physicist who made significant contributions to the study of electromagnetic waves.

Another unit that is sometimes used to express linear frequency is revolutions per minute (RPM). This unit is commonly used in the context of rotating machinery, such as engines or motors. It represents the number of complete rotations that occur in one minute.

To better understand the relationship between Hertz and RPM, consider a rotating object that completes one full revolution every second. In this case, the linear frequency would be 1 Hz or 60 RPM, as there are 60 seconds in a minute.

Symbol Used to Represent Linear Frequency

In mathematical equations and scientific notations, linear frequency is typically represented by the symbol “f” or the Greek letter “ν” (nu). The symbol “f” is derived from the word “frequency” and is widely used in various scientific disciplines.

The Greek letter “ν” is often used as an alternative symbol for linear frequency. It is derived from the Greek word “νεῦμα” (neuma), which means “nod” or “vibration.” The use of this symbol adds a touch of elegance and mathematical convention to the representation of linear frequency.

Both “f” and “ν” are widely recognized and accepted symbols for linear frequency in scientific literature and engineering applications. They are used interchangeably depending on the preference of the author or the field of study.

To summarize, linear frequency is measured in Hertz (Hz) or revolutions per minute (RPM). The symbol “f” or the Greek letter “ν” is used to represent linear frequency in mathematical equations and scientific notations. Understanding these units and symbols is essential for comprehending and working with linear frequency in various applications.

Angular Frequency vs Linear Frequency

Explanation of Angular Frequency and Linear Frequency

When discussing the concept of frequency, it is important to understand the difference between angular frequency and linear frequency. While both terms are related to the measurement of cycles or oscillations per unit of time, they are used in different contexts and have distinct meanings.

Angular Frequency:

Angular frequency, denoted by the symbol ω (omega), is a measure of how quickly an object or system rotates or oscillates. It is expressed in radians per second (rad/s). Angular frequency is commonly used in physics and engineering to describe the rate of change of angular displacement over time.

To better understand angular frequency, let’s consider an example. Imagine a wheel rotating at a constant speed. The angular frequency would represent how fast the wheel is turning, measured in radians per second. A higher angular frequency would indicate a faster rotation, while a lower angular frequency would correspond to a slower rotation.

Linear Frequency:

On the other hand, linear frequency, often simply referred to as frequency, is a measure of how many cycles or oscillations occur in a given unit of time. It is commonly denoted by the symbol f and expressed in hertz (Hz). Linear frequency is widely used in various fields, including physics, electronics, and telecommunications.

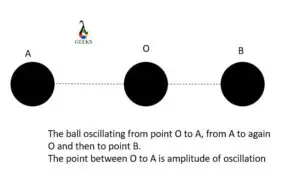
To illustrate linear frequency, let’s consider a simple example. Imagine a pendulum swinging back and forth. The linear frequency would represent how many complete swings the pendulum makes in one second. A higher linear frequency would indicate a faster oscillation, while a lower linear frequency would correspond to a slower oscillation.

Relationship between Angular Frequency and Linear Frequency

Although angular frequency and linear frequency have different units of measurement, they are closely related. In fact, there is a direct mathematical relationship between the two.

The relationship between angular frequency (ω) and linear frequency (f) can be expressed using the formula:

ω = 2πf

Here, π (pi) is a mathematical constant approximately equal to 3.14159. By multiplying the linear frequency by 2π, we can obtain the corresponding angular frequency.

This relationship allows us to convert between angular frequency and linear frequency. For example, if we know the linear frequency of a signal, we can easily calculate its angular frequency using the formula mentioned above.

Comparison of Symbols and Units Used for Angular Frequency and Linear Frequency

Angular frequency and linear frequency are represented by different symbols and units. Understanding these symbols and units is essential for correctly interpreting and working with frequency-related measurements.

Here is a comparison of the symbols and units used for angular frequency and linear frequency:

	Angular Frequency	Linear Frequency
Symbol	ω (omega)	f
Unit	radians per second (rad/s)	hertz (Hz)

As shown in the table, angular frequency is represented by the symbol ω (omega) and measured in radians per second (rad/s). On the other hand, linear frequency is denoted by the symbol f and expressed in hertz (Hz).

It is important to note that while angular frequency and linear frequency have different symbols and units, they are both fundamental concepts in the study of oscillations and waves. Understanding their relationship and how to convert between them is crucial in various scientific and engineering applications.

Finding Linear Frequency

Formulas for calculating linear frequency

When it comes to understanding linear frequency, there are a few formulas that can help us calculate it. Linear frequency refers to the rate at which a signal oscillates or repeats over time. It is an essential concept in various fields, including physics, engineering, and signal processing.

One of the most common formulas used to calculate linear frequency is:

f = 1 / T

In this formula, f represents the linear frequency, and T represents the period of the signal. The period is the time it takes for one complete cycle of the signal to occur. By taking the reciprocal of the period, we can determine the linear frequency of the signal.

Another formula that is often used is:

f = n / t

Here, f represents the linear frequency, n represents the number of cycles that occur in a given time period t. This formula allows us to calculate the linear frequency based on the number of cycles that occur within a specific time frame.

Examples of calculating linear frequency for different scenarios

Let’s explore a few examples to better understand how to calculate linear frequency in different scenarios.

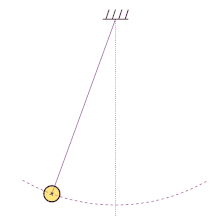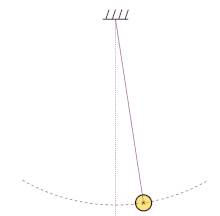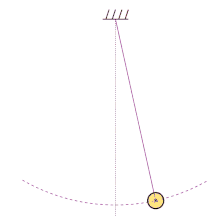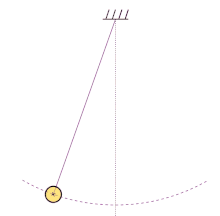
Example 1: Simple Harmonic Motion

Consider a simple harmonic motion, such as a mass attached to a spring oscillating back and forth. If the period of this motion is 2 seconds, we can use the formula f = 1 / T to calculate the linear frequency:

f = 1 / 2
f = 0.5 Hz

Therefore, the linear frequency of this simple harmonic motion is 0.5 Hz.

Example 2: Sound Waves

In the context of sound waves, the linear frequency represents the pitch of the sound. Suppose we have a sound wave with a period of 0.01 seconds. Using the formula f = 1 / T, we can calculate the linear frequency:

f = 1 / 0.01
f = 100 Hz

Hence, the linear frequency of this sound wave is 100 Hz.

Example 3: Electrical Signals

Electrical signals also have linear frequencies that can be calculated using the formulas mentioned earlier. Let’s say we have an electrical signal with a period of 0.005 seconds and it completes 10 cycles within that time frame. Using the formula f = n / t, we can determine the linear frequency:

f = 10 / 0.005
f = 2000 Hz

Therefore, the linear frequency of this electrical signal is 2000 Hz.

By applying these formulas, we can calculate the linear frequency for various scenarios, whether it’s simple harmonic motion, sound waves, or electrical signals. Understanding linear frequency allows us to analyze and manipulate signals in different domains, such as audio processing, telecommunications, and radar systems.

Importance of Frequency

Explanation of the Significance of Frequency in Physics

Frequency is a fundamental concept in physics that plays a crucial role in understanding various phenomena. It refers to the number of cycles or oscillations of a wave that occur in a given time period. Whether we are talking about sound waves, light waves, or electrical signals, frequency is a key parameter that helps us analyze and comprehend these phenomena.

In physics, frequency is measured in hertz (Hz), which represents the number of cycles per second. The higher the frequency, the more cycles occur within a given time frame. Conversely, a lower frequency means fewer cycles occur in the same time period.

Frequency is significant in physics for several reasons. Firstly, it helps us determine the pitch of sound waves. For example, a high-frequency sound wave corresponds to a high-pitched sound, while a low-frequency sound wave corresponds to a low-pitched sound. This relationship between frequency and pitch is crucial in music, as different frequencies produce different musical notes.

Secondly, frequency is essential in analyzing and understanding wave phenomena. Waves, such as water waves, electromagnetic waves, and seismic waves, all exhibit characteristic frequencies. By studying the frequency of these waves, scientists can gain insights into their behavior, propagation, and interaction with the surrounding environment.

Lastly, frequency is vital in the field of electronics and electrical engineering. In alternating current (AC) circuits, the frequency of the electrical signal determines the rate at which the current alternates direction. This is particularly important in power distribution systems, where a consistent frequency is necessary for efficient transmission and operation of electrical devices.

Applications of Frequency in Various Phenomena

Frequency finds applications in a wide range of phenomena, including oscillation, waves, light, current, and voltage. Let’s explore some of these applications:

1. Oscillation: Frequency is central to the study of oscillatory motion. Whether it’s the swinging of a pendulum, the vibrations of a guitar string, or the motion of a simple harmonic oscillator, the frequency determines the rate at which the system oscillates. In simple terms, it determines how fast or slow an object vibrates back and forth.

2. Waves: Frequency is a fundamental property of waves. It determines the number of wave cycles that pass through a given point in a unit of time. For example, in the case of water waves, the frequency determines the number of wave crests that pass a fixed point in a second. In electromagnetic waves, such as radio waves, microwaves, and visible light, frequency determines the energy and wavelength of the wave.

3. Light: In the context of light, frequency determines its color. Different colors of light correspond to different frequencies. For instance, red light has a lower frequency than blue light. This relationship between frequency and color is essential in fields like optics, photography, and display technologies.

4. Current and Voltage: In electrical circuits, frequency plays a crucial role in determining the behavior of current and voltage. For example, in alternating current (AC) circuits, the frequency of the electrical signal determines the rate at which the current alternates direction. This is important in the design and operation of electrical devices, such as motors, generators, and transformers.

Understanding the importance of frequency in these various phenomena allows scientists, engineers, and researchers to manipulate and control these phenomena for practical applications. By manipulating the frequency, we can achieve desired outcomes, such as amplification, filtering, or modulation of signals.

Linear Frequency Modulation

Linear frequency modulation, also known as linear FM, is a modulation technique commonly used in various applications such as radar and pulse compression. It involves a continuous change in frequency over time, resulting in a linear relationship between the frequency and time. This section will provide a definition and explanation of linear frequency modulation, as well as explore its applications in radar and pulse compression.

Definition and Explanation of Linear Frequency Modulation

Linear frequency modulation is a method of modulating a carrier signal by varying its frequency in a linear manner. In this technique, the frequency of the carrier signal increases or decreases at a constant rate over time. The rate at which the frequency changes is known as the sweep rate or modulation rate.

One of the key characteristics of linear frequency modulation is that the frequency change is proportional to the time elapsed. This means that the frequency increases or decreases linearly with time. This linear relationship between frequency and time allows for precise control and manipulation of the carrier signal.

Linear frequency modulation is often used in various applications that require the transmission and reception of signals with specific frequency characteristics. It is particularly useful in radar systems and pulse compression techniques.

Applications of Linear Frequency Modulation in Radar and Pulse Compression

Radar systems utilize linear frequency modulation to accurately measure the distance and velocity of objects. By transmitting a signal with a linearly increasing or decreasing frequency, the radar system can calculate the time it takes for the signal to travel to the target and back. This information is then used to determine the distance to the target.

In pulse compression techniques, linear frequency modulation is employed to improve the resolution and range of radar systems. By using a linear frequency modulated signal, the radar system can achieve a compressed pulse with a longer duration. This extended pulse duration allows for better range resolution, enabling the detection of smaller targets and improved accuracy.

Linear frequency modulation is also utilized in sonar systems for underwater communication and object detection. By modulating the frequency of the sonar signal in a linear manner, it is possible to accurately measure the distance to underwater objects and detect their presence.

Frequency Separation in Photoshop

Frequency separation is a powerful technique used in image editing to separate the high-frequency details from the low-frequency tones in an image. This technique allows for precise control and manipulation of different aspects of an image, such as texture and color, without affecting the overall composition. In this section, we will explore the concept of frequency separation in Photoshop and discuss its importance and applications in image editing.

Explanation of Frequency Separation in Photoshop

Frequency separation works by decomposing an image into two separate layers: the high-frequency layer and the low-frequency layer. The high-frequency layer contains the fine details of the image, such as wrinkles, pores, and texture, while the low-frequency layer contains the broader tonal information, such as color transitions and gradients.

To create a frequency separation in Photoshop, follow these steps:

1. Open the image you want to edit in Photoshop.
2. Duplicate the image layer twice.
3. Rename the first duplicate layer as “High Frequency” and the second duplicate layer as “Low Frequency.”
4. Apply a high-pass filter to the “High Frequency” layer. This filter helps to enhance the details by removing the low-frequency information. Adjust the radius of the filter to control the level of detail.
5. Apply a Gaussian blur filter to the “Low Frequency” layer. This filter helps to smooth out the image and preserve the overall tonal information. Adjust the radius of the filter to control the level of smoothness.
6. Set the blending mode of the “High Frequency” layer to “Linear Light.” This blending mode allows the layer to interact with the layers below it while preserving the details.
7. Now, you can make adjustments to each layer separately. For example, you can use the healing brush tool on the “High Frequency” layer to remove blemishes and imperfections without affecting the overall color and tone of the image. On the other hand, you can adjust the brightness, contrast, and color balance on the “Low Frequency” layer to enhance the overall look of the image.

Importance and Application of Frequency Separation in Image Editing

Frequency separation is a valuable technique in image editing because it provides a non-destructive way to retouch and enhance images. By separating the high-frequency details from the low-frequency tones, photographers and retouchers can have more control over the editing process, resulting in more natural and realistic-looking images.

Here are some important applications of frequency separation in image editing:

1. Skin Retouching: Frequency separation is widely used in portrait retouching to smooth out skin imperfections while preserving the texture. By working on the high-frequency layer, retouchers can remove blemishes, wrinkles, and other skin flaws without affecting the overall skin tone and color.

2. Texture Enhancement: Frequency separation allows photographers to enhance the texture in their images. By selectively sharpening the high-frequency layer, they can bring out the fine details and make the image more visually appealing.

3. Color Correction: With frequency separation, it is possible to adjust the color and tone of an image without affecting the texture. By working on the low-frequency layer, photographers can make global color corrections, such as adjusting the white balance, saturation, and contrast, while leaving the fine details intact.

4. Object Removal: Frequency separation can be used to remove unwanted objects from an image seamlessly. By cloning or healing on the high-frequency layer, retouchers can remove distractions without leaving any visible traces.

Linear Frequency Modulation Waveform Synthesis

Explanation of Waveform Synthesis using Linear Frequency Modulation

Waveform synthesis using linear frequency modulation (LFM) is a technique that involves varying the frequency of a signal in a linear manner over time. This modulation technique is widely used in various applications, including radar, sonar, telecommunications, and music synthesis.

In LFM, the frequency of the signal increases or decreases linearly with time. This results in a continuous and smooth change in the pitch or frequency of the waveform. The rate at which the frequency changes is known as the sweep rate or chirp rate. By controlling the sweep rate, we can shape the characteristics of the synthesized waveform.

One common way to generate an LFM waveform is by using a voltage-controlled oscillator (VCO). The VCO produces a signal with a frequency that is directly proportional to the input voltage. By applying a linearly increasing or decreasing voltage to the VCO, we can achieve the desired linear frequency modulation.

Another method for LFM waveform synthesis is through digital signal processing techniques. By manipulating the digital representation of the waveform, we can achieve precise control over the frequency modulation. This approach is commonly used in software-based synthesizers and digital communication systems.

Applications and Benefits of Linear Frequency Modulation in Waveform Synthesis

Linear frequency modulation has a wide range of applications in various fields. Let’s explore some of the key applications and the benefits it offers:

1. Radar Systems: LFM is extensively used in radar systems for target detection and ranging. By transmitting LFM waveforms and analyzing the received signals, radar systems can accurately measure the distance to objects and detect their velocity. The linear frequency modulation allows for better resolution and range accuracy in radar systems.

2. Sonar Systems: Similar to radar, sonar systems also utilize LFM waveforms for underwater target detection and ranging. By emitting LFM signals and analyzing the echoes, sonar systems can determine the distance and location of underwater objects. The linear frequency modulation helps in distinguishing between different targets and reducing interference from reflections.

3. Telecommunications: LFM is employed in various telecommunications applications, such as frequency-modulated continuous wave (FMCW) radar and spread spectrum communication systems. In FMCW radar, LFM waveforms are used to measure the range and velocity of targets. Spread spectrum communication systems utilize LFM waveforms to achieve robust and secure communication by spreading the signal energy across a wide frequency band.

4. Music Synthesis: LFM is widely used in electronic music synthesis to create unique and evolving sounds. By modulating the frequency of oscillators with LFM waveforms, musicians can generate complex and dynamic timbres. The linear frequency modulation adds movement and expressiveness to the synthesized sounds, allowing for rich and evolving musical compositions.

5. Medical Imaging: LFM waveforms find applications in medical imaging techniques, such as ultrasound and magnetic resonance imaging (MRI). In ultrasound imaging, LFM signals are used to generate focused beams and improve the resolution of the images. In MRI, LFM waveforms are employed to encode spatial information and reconstruct detailed images of the body.

The benefits of using linear frequency modulation in waveform synthesis include improved resolution, enhanced range accuracy, better target detection, reduced interference, and the ability to create dynamic and evolving sounds. These advantages make LFM a versatile and powerful technique in various fields.

Linear Frequency Response

Definition and Explanation of Linear Frequency Response

In signal processing, the concept of linear frequency response plays a crucial role. It refers to the behavior of a system or device when subjected to different frequencies of input signals. A linear frequency response means that the system or device responds uniformly to all frequencies within its operating range.

When we talk about linear frequency response, we are essentially looking at how a system or device handles different frequencies without distorting the input signal. In simpler terms, it means that the output of the system or device is a faithful reproduction of the input signal, with no alterations in amplitude or phase.

To understand this concept better, let’s consider an example. Imagine you have a speaker system that claims to have a linear frequency response from 20 Hz to 20 kHz. This means that when you feed the speaker system with a sine wave at 50 Hz, it will produce an output that accurately represents the input signal. Similarly, if you input a sine wave at 10 kHz, the speaker system will faithfully reproduce that frequency as well.

Importance and Applications of Linear Frequency Response in Signal Processing

The concept of linear frequency response is of utmost importance in various fields of signal processing. Let’s explore some of its applications:

1. Audio Equipment: In the realm of audio, linear frequency response is crucial for high-fidelity reproduction of sound. Audio systems such as speakers, headphones, and amplifiers strive to achieve a linear frequency response to ensure accurate playback of music and other audio content. This ensures that the listener hears the audio as intended by the artist or sound engineer.

2. Telecommunications: Linear frequency response is vital in telecommunications systems, including telephones, cell phones, and VoIP (Voice over Internet Protocol) devices. These systems rely on accurate transmission and reception of audio signals, and a linear frequency response ensures that the transmitted voice signals are faithfully reproduced at the receiving end.

3. Equalization: Equalization is a technique used to adjust the frequency response of audio systems to compensate for deficiencies in the system or to achieve a desired sound. Linear frequency response is essential in equalization to ensure that the adjustments made to the frequency spectrum do not introduce distortion or alter the original sound beyond the intended modifications.

4. Instrumentation: Linear frequency response is crucial in various scientific and engineering instruments. For example, oscilloscopes, spectrum analyzers, and data acquisition systems need to accurately measure and display signals across a wide range of frequencies. A linear frequency response ensures that the measurements and analysis performed by these instruments are reliable and accurate.

Linear Frequency Modulation Chirp

Definition and Explanation of Linear Frequency Modulation Chirp

Linear Frequency Modulation Chirp is a technique used in various fields, such as radar, sonar, telecommunications, and audio synthesis. It involves the modulation of a signal’s frequency in a linear manner over time. This modulation creates a distinctive sound or waveform known as a chirp.

A chirp is characterized by a continuous change in frequency over a specified time period. Unlike a simple tone, which has a constant frequency, a chirp sweeps through a range of frequencies, either increasing or decreasing linearly. This linear frequency modulation allows for a wide range of applications and benefits.

One of the key aspects of linear frequency modulation chirp is the linear relationship between the frequency and time. As time progresses, the frequency of the chirp changes at a consistent rate. This linear relationship makes it easier to analyze and process the chirp signal.

Applications and Benefits of Linear Frequency Modulation Chirp

Linear frequency modulation chirp finds applications in various fields due to its unique properties and benefits. Let’s explore some of the key applications and advantages of this technique:

1. Radar and Sonar Systems: Linear frequency modulation chirp is widely used in radar and sonar systems for target detection and ranging. By transmitting a chirp signal and analyzing the received echo, these systems can accurately determine the distance, velocity, and direction of objects. The linear frequency modulation allows for precise measurements and improved target detection in noisy environments.

2. Telecommunications: In telecommunications, linear frequency modulation chirp is used for channel estimation and equalization. By transmitting chirp signals through a communication channel, the system can analyze the received signal to estimate the channel‘s frequency response. This information is crucial for equalizing the channel and improving the overall communication quality.

3. Audio Synthesis: Linear frequency modulation chirp is also utilized in audio synthesis to create unique and dynamic sounds. By modulating the frequency of an oscillator in a linear manner, composers and sound designers can generate interesting and evolving timbres. This technique is commonly used in electronic music and sound effects production.

4. Medical Imaging: Linear frequency modulation chirp is employed in medical imaging techniques such as ultrasound and magnetic resonance imaging (MRI). In ultrasound imaging, chirp signals are used to generate focused beams and improve image resolution. In MRI, chirp pulses are utilized for spatial encoding and signal acquisition.

5. Geophysical Exploration: Linear frequency modulation chirp is used in geophysical exploration, particularly in seismic surveys. By transmitting chirp signals into the ground and analyzing the reflected waves, geophysicists can gather information about subsurface structures and geological formations. The linear frequency modulation allows for better resolution and depth penetration.

6. Non-Destructive Testing: Linear frequency modulation chirp is applied in non-destructive testing (NDT) methods like ultrasonic testing. By transmitting chirp signals into materials and analyzing the reflected waves, defects and anomalies can be detected. The linear frequency modulation helps in distinguishing between different types of reflections and improving the accuracy of defect identification.

Linear Frequency Calculator

A linear frequency calculator is a useful tool that helps in determining the frequency of a signal or waveform. It is particularly helpful in fields such as electronics, telecommunications, and audio engineering. Understanding the concept of linear frequency is essential to comprehend how this calculator works.

Linear frequency refers to a frequency scale that increases or decreases in a linear manner. In other words, the frequency values are evenly spaced apart. This is in contrast to logarithmic frequency scales, where the spacing between values increases exponentially. The linear frequency scale is commonly used in applications where a linear relationship between frequency and some other parameter is desired.

Explanation of How to Use a Linear Frequency Calculator

Using a linear frequency calculator is straightforward and requires only a few simple steps. Let’s walk through the process:

1. Input the Start and End Frequencies: The first step is to input the start and end frequencies of the desired range. These frequencies define the span over which the linear frequency calculator will operate. For example, if you want to analyze frequencies from 100 Hz to 10 kHz, you would enter these values accordingly.

2. Specify the Number of Steps: Next, you need to specify the number of steps or intervals you want the linear frequency calculator to divide the range into. This determines the resolution or granularity of the frequency values. A higher number of steps will result in a more detailed analysis but may require more computational resources.

3. Calculate the Step Size: The step size is calculated by dividing the difference between the end and start frequencies by the number of steps. This value represents the increment between each frequency value in the linear scale.

4. Generate the Frequency Values: Once the step size is determined, the linear frequency calculator generates the frequency values within the specified range. These values are evenly spaced apart and cover the entire span from the start to the end frequency.

5. Utilize the Frequency Values: The generated frequency values can now be used for various purposes, such as analyzing the frequency response of a system, designing filters, or generating test signals. The linear frequency scale allows for easy interpretation and comparison of different frequency components.

Using a linear frequency calculator simplifies the process of working with frequency values and enables efficient analysis and manipulation of signals. It eliminates the need for manual calculations and ensures accuracy in determining the frequency range of interest.

Frequently Asked Questions

Q1: What is linear frequency modulation?

A1: Linear frequency modulation is a technique where the frequency of a signal varies linearly with time.

Q2: How is linear frequency modulation synthesized?

A2: Linear frequency modulation synthesis is achieved by varying the frequency of a waveform in a linear manner over time.

Q3: What is linear frequency modulation radar?

A3: Linear frequency modulation radar is a radar system that uses linear frequency modulation to transmit and receive signals, allowing for accurate range and velocity measurements.

Q4: How does linear frequency modulation sonar work?

A4: Linear frequency modulation sonar uses linear frequency modulation to transmit and receive sound waves in water, enabling the detection and location of underwater objects.

Q5: What is the linear frequency modulation equation?

A5: The linear frequency modulation equation describes the relationship between the frequency of a signal and time, typically represented as f(t) = f0 + kt, where f0 is the initial frequency and k is the rate of change.

Q6: Why is frequency important?

A6: Frequency is important because it determines the pitch of a sound or the rate of occurrence of a repeating event, and it is a fundamental parameter in many fields such as communication, signal processing, and physics.

Q7: How does the linear frequency response change when frequency increases?

A7: The linear frequency response describes how a system or device responds to different frequencies. When frequency increases, the linear frequency response may change, resulting in variations in amplitude, phase, or other characteristics of the system’s output.

Q8: What is the ratio of angular frequency and linear frequency?

A8: The ratio of angular frequency (ω) to linear frequency (f) is given by the equation ω = 2πf, where 2π represents a full cycle or 360 degrees.

Q9: How can I calculate the linear frequency?

A9: The linear frequency can be calculated using the formula f = 1/T, where f is the frequency and T is the period of the waveform.

Q10: Why would I want to linearize data?

A10: Linearizing data is often done to simplify analysis or modeling. By transforming non-linear data into a linear form, it becomes easier to apply linear regression techniques or make linear approximations for further analysis.

The periodic motion of an object, particle, or quantity at regular intervals about a mean position is known as oscillation. 

When a body oscillates, it comprises linear as well as angular displacement, this angular displacement is known as angular frequency of oscillation. There are also other terms in physics for angular frequency such as angular speed orbital frequency. 

The angular frequency is the scalar measure of the angular displacement of an oscillating particle. For sinusoidal waves, it is referred to as the rate of phase change. When a ball tied to a rope is rotated in a circular motion, the rate at which it completes one oscillation of 360 degrees is known as the angular frequency. 

Angular Frequency of Oscillation Formula

The change in angle that occurs in one second is termed angular frequency. Hence the basic formula to derive the angular frequency is;

Here;

ω is the angular frequency

Θ is the angle through which an object is displaced. 

t is for the time taken. 

For the simple harmonic motion or simply oscillation, the formula of angular frequency is derived by multiplying the linear frequency with the angle that is covered by oscillating particles. For one complete cycle, the angle is 2π. Hence the formula for angular frequency becomes;

ω =2πf

Using the relationship between frequency and time period in the above equation the formula becomes; 

Since angular frequency is angular displacement rate, its unit becomes radian per unit time, that is;

Angular Frequency of Oscillation Spring

In the above spring-mass system, on adding the load, the spring displaces to distance y, and the oscillation stretches it to a further x position. 

According to Hooke’s law.

From the diagram, we can see that

From the free body diagram, we can see that weight is acting downward. Inertia force that is ma is acting upward, and restoring force that is k(x+y) is also acting upward.

We will get:

We know that W=ky; hence we get:

Dividing by m:

On comparing it with the SHM equation, we get:

This is the angular frequency of the spring oscillation. 

Angular Frequency Of Oscillation Pendulum

A pendulum is a small bob tied to a thread. It swings to generate oscillation. The amplitude of pendulum oscillation is measured as the maximum displacement that a bob covers starting from the central position. In a simple pendulum, the mass of the string is negligible compared to the mass of the bob. 

Through the figure above, we can see the forces acting on the bob of the pendulum. The gravitational weight is acting downwards. The restoring torque acting on the pendulum is the element of the weight of the bob. From the figure, we get the value of torque as; 

For every small angle we have;

Hence we get; 

Comparing it with the simple harmonic motion equation: 

We get:

Here;

g is the acceleration due to gravity, and L is the length of the pendulum.

Angular Frequency of Oscillation Of The Object

For an oscillating object, the SHM equation is given as:

Here;

x is the displacement of the object 

A is the amplitude of the oscillation 

???? is the phase change

ω is the angular frequency 

For the oscillating object, the angular frequency is given as; 

ω =2πf

It tells about how much angle the object is rotating for displacing. 

How to Find Angular Frequency of Oscillation 

For the different objects and scenarios, a different formula is used to calculate the angular frequency of oscillation. 

For instance, the amplitude of the oscillation is given to be 0.14m; the phase change is 0.  Now to cover 14 cm in 8.5 seconds, the angular frequency is calculated using the formula;

For calculating the angular frequency of the pendulum, the formula used is; 

For example, if the length of the pendulum is 10 cm, then the angular frequency of oscillation is;

To calculate the angular frequency of spring, the formula is:

If the spring constant is given to 2 N/m and mass is given to be 8 kg, then the angular frequency would be;

Frequently Asked Questions (FAQs)

What is the angular frequency of oscillation?

The repetitive motion of a particle about a fixed point is known as oscillation. 

The angle change of the particle is the angular frequency of oscillation. In physics, it is also termed the rate of change of phase. It is a scalar element as it is just the angular displacement without any direction. The formula for the angular frequency is given as;

ω =2πf

How is angular frequency is related to the time period?

The oscillating objects are comprised of both linear displacements as well as angular displacement. 

The basic formula for angular frequency is given as;

It shows the relation of time and angular frequency of oscillation. 

Now the general formula for angular frequency is:

ω =2πf

Substituting the given relation

We get;

This equation relates angular frequency and time period. 

What is the unit of angular frequency?

The angular frequency is the change in angle of the oscillating particle in unit time. 

The unit of the angular frequency is given as radian per unit sec such as;

When the object covers one complete cycle in one second, then the angular frequency becomes 1. 

Is angular frequency the same as frequency?

The number of oscillations the object makes in one second is known to be the frequency. 

No, the frequency and angular frequency are not the same things. Angular frequency is the change in the angle of the oscillating particle in unit time, whereas the frequency is the oscillation made in one second.  They both are different terms used for a different concept of physics. 

The regular change of the physical quantity about the central points is known as oscillation. The state is changed between two extreme points.

The maximum displacement of the oscillation from the mean position to either side of points is known as the amplitude of oscillation. It is also stated as the magnitude of change of oscillating quantity.

The constant to and fro movement of any variable or object between two fixed points is known as oscillation. The peak value or displacement that the oscillating object reaches is known as its amplitude. The pendulum, springs, guitar strings are all examples of oscillation. In the figure given above, the ball moves from point O to point A and then from there to point O then to B. On calculating the length between O and A or O and B we get the amplitude of the oscillation.

Amplitude of oscillation formula

The amplitude of oscillation is represented as A. For the full range oscillation, the magnitude is derived as 2A. Since oscillation is a periodic function, its wave equation is represented as a sine or cosine function. The formula for the amplitude of the oscillation is; 

x = A sin ωt

or

x = A cos ωt

x is the displacement of the particle

A is the maximum amplitude

ω is the angular frequency

t is the time interval

Φ is phase shift

Frequency of oscillation units

The frequency provides you with the knowledge of oscillations made per unit second. It is also stated as the cycle completed in 1 second. One cycle means one complete oscillation.

The frequency is represented as f. The relationship between the frequency and time period is given as;

f = 1/T

f is the frequency and T is the time period of the oscillation.

The S.I unit of frequency is given as;

f = 1 cycle / 1 second

Hence the unit of frequency is Hertz, Hz.

Amplitude of oscillation spring

The motion of a spring is an example of oscillation. When we press or pull the spring, it comes into continuous motion. This type of continuous motion is known as simple harmonic motion.

The spring can be in two arrangements;

• Vertical system
• Horizontal system

Vertical System

Here as shown in the figure, the string is fixed at a point and hanging vertically. When the load hangs on the spring it stretches to the length y and then starts oscillating. The figure shows the maximum and minimum displacement as +A and -A.

The angular frequency is given as:

t = k/m

Where;

t = 2f

The solution equation of the spring oscillation is:

x = A sin ωt

Horizontal System

The amplitude of any kind of simple harmonic motion is using the given equation;

x = A sin ωt

The energy changes at every point between kinetic and potential energy. The total energy always remains constant. Hence, we get;

E_total = U + k

The position and velocity equation of the oscillation is defined as;

x = A cos ωt

Using the trigonometric identity:

cos² + sin² = 1

and

ω² = k/m

We get:

E_total = 1/2 KA²

This equation represents the relationship between the total energy of the spring system and the amplitude. Hence the given equation is used to calculate the amplitude of spring oscillation.

Amplitude of oscillation pendulum

A pendulum is a small bob tied to a thread. It swings to generate oscillation. The amplitude of pendulum oscillation is measured as the maximum displacement that a bob covers starting from the central position. The central position is the initial position of the bob when it is in the rest position. Some refer to this as origin or equilibrium position. The pendulum moves back and forth starting from this point. The largest distance that the bob covers on either side is its “amplitude.” On both sides, the amplitude remains the same. For instance, if a bob covers 3 cm on the left side, it will displace to the same extent on the right side.

Amplitude of oscillation units

The ampitude is the maximum length that a particle covers from its equilibrium position. Since amplitude is a distance travelled hence its unit is a meter that is ‘m’. The meter is the standard unit of amplitude, but other units are also used. Kilometre km’, centimetre cm,’ and millimetre mm’ are some other units.

Amplitude of oscillation of simple pendulum

The simple pendulum is a particular type of pendulum whose bob’s size is much smaller than the distance of the object’s centre of gravity and point of suspension. The amplitude of the simple pendulum does not have any effect on the time period. With the increase in amplitude, the restoring force also increases, which cancels out the effect.

On comparing the oscillation of simple pendulum with the uniform circular motion  we get the following solution equation;

x = A cos ωt

x for instantaneous displacement

ω is the angular frequency

t is for time intervals.

This equation is used when the starting point of the pendulum oscillation is taken as the extreme point. In case the oscillation starts from the mean position, the equation becomes;

x = A sin ωt

Amplitude of oscillation diagram

Oscillation is a simple harmonic motion whose equation can be represented as a function of sine and cosine. Hence its diagram is depicted as a wave graph.

If an oscillating variable undergoes regular back and forth motion, then the peak value that the particle displaces gives out the amplitude of the variable. For all types of diagrams, the amplitude remains the same: the maximum displacement of waves.

Amplitude of oscillation of a particle

The absolute length of vibration or displacement of a sinusoidal oscillation from the equilibrium position is its amplitude. It is the maximum size of a periodically varying particle. The difference of any physical particle from its extreme position and mean position determines its amplitude.

It simply tells us the magnitude of the particle oscillation. The formula for sinusoidal oscillations is;

y = A sin ωt

where | A | is the absolute value of A.

The amplitude variable represents a sinusoidal oscillation. It provides the deflection of a particle from its mean point to a positive or negative value. The particle displacement is particle amplitude. A transverse wave can be described with its distinguished amplitude. Every particle frequency, such as a string, pendulum, and spring, has an amplitude.

How to find amplitude of oscillation

To find the amplitude of oscillation, the general formula used is;

x = A sin ωt + Φ

Where,

x is the displacement of the particle

A is the maximum amplitude

ω  is the angular frequency

t is the time interval

Φ is a phase shift.

For instance, a pendulum is swinging with angular speed = π radians and phase shift = 0. Then the amplitude of the pendulum, which covers 14 cm in 8.50 seconds are;

x = A sin ωt + Φ = A sint (0.14*0.85) + 0 = 146 cm

Then the amplitude can be easily found by examining the equation. In this case, the amplitude is 6.

The next case is when the graph of the oscillation is provided. Here we can see the maximum displacement of the wave on either side is. Hence the amplitude is 5.

Frequency of oscillation of a spring-mass system

In the above spring-mass system on adding the load the spring displaces to distance y and the oscillation stretches it to a further x position.

According to Hooke’s law.

F=ky

From the diagram, we can see that

W = mg = ky

From the free body diagram, we can see that weight is acting downward. Inertia force that is ma is acting upward and restoring force that is k(x+y) is also acting upward.

We will get:

ma + k (x+y) – W = 0

We know that  W= ky, hence we get:

ma + kx = 0

Dividing by m:

a + k/m x = 0

On comparing it with the SHM equation we get:

f = 1/2 √k/m

This is the frequency of the spring-mass system oscillation. 

Frequently Asked Questions (FAQs)

What is oscillation?

The oscillation occurs in every area of physics and day-to-day life.

The oscillation is the repetitive too and fro motion of a particle, object, or quantity in time. The oscillating particles move about the mean position to the extreme points on either side. Simple pendulum, spring, playground swings are all examples of oscillation.

How are oscillation and periodic motion different?

The motion can be of two types oscillation or periodic motion.

The periodic motion is the regular movement of a particle at regular intervals. At the same time, oscillation is just the back-and-forth motion of a vibrating object. Every oscillatory motion is periodic, but the converse need not be true. The earth revolves around the sun, which is a periodic function as it keeps repeating itself after a fixed time. A swing is an oscillatory object.

What is the amplitude of oscillation?

The repetitive motion of a particle is known as oscillation.

The extent to which a particle can displace is its amplitude. The displacement is measured from the mean position to either side of the extreme position. ‘A’ represents the amplitude of oscillation, and its standard unit is meter.

Is oscillation a simple harmonic motion?

The motion proportional to the displacement and under the effect of retarding force is known as simple harmonic motion.

The SHM is an oscillatory motion. Or we can say that oscillation is a simple harmonic motion. For example, the spring moves under the influence of Hooke’s law, and its motion is proportional to displacement. Hence it is an SHM oscillation.

What is the equation of oscillating particles?

The oscillation is the simple harmonic motion.

The equation of oscillation is as follow;

x = A sin ωt + Φ

Where,

x is the displacement of the particle

A is the maximum amplitude

 ω is the angular frequency

t is the time interval

Φ  is phase shift

In physics, understanding the magnitude of net force is crucial for analyzing the motion of objects. net force refers to the combined effect of all the forces acting on an object. In this blog post, we will explore how to calculate the magnitude of net force, determine its direction, and calculate the magnitude of resultant force. We will cover the concepts, formulas, and provide worked-out examples to help you grasp the core ideas quickly and easily. So, let’s dive into the world of forces and learn how to find the magnitude of net force step by step.

How to Calculate the Magnitude of Net Force

Identifying the Forces Acting on an Object

To calculate the magnitude of net force, we must first identify all the forces acting on an object. forces can be classified into various types, such as gravitational force, frictional force, normal force, and applied force. Each force has its own unique characteristics, and they can either act in the same direction or in opposite directions.

Understanding the Direction of Forces

Before calculating the magnitude of net force, it is essential to understand the direction of forces. forces are vector quantities, which means they have both magnitude and direction. To determine the net force, we need to consider the sign or direction of each force. forces acting in the same direction can be added together, while forces acting in opposite directions can be subtracted from each other.

The Mathematical Approach to Calculating Net Force

The net force is the vector sum of all the forces acting on an object. To calculate the magnitude of net force, we can use the following formula:

Here, (F_1, F_2, F_3, …, F_n) represent the individual forces acting on the object. The net force is the total of all these forces.

Worked Out Examples on Finding the Magnitude of Net Force

Example of Calculating Net Force in Linear Motion

Let’s consider an example to illustrate how to calculate the magnitude of net force in linear motion. Suppose a car is experiencing two forces: an applied force of 500 N in the forward direction and a frictional force of 200 N in the opposite direction. To find the net force, we can subtract the frictional force from the applied force:

 

Therefore, the magnitude of the net force acting on the car is 300 N.

Example of Calculating Net Force in Circular Motion

In circular motion, an object experiences a net force towards the center of the circle, known as the centripetal force. Let’s consider an example where a car is moving in a circular path with a radius of 10 meters at a constant speed of 20 m/s. The mass of the car is 1000 kg. To calculate the magnitude of net force, we can use the formula:

Substituting the given values, we have:

Therefore, the magnitude of the net force acting on the car in circular motion is 40000 N.

Example of Calculating Net Force without Acceleration

Sometimes, an object may experience forces that cancel each other out, resulting in no net force. Let’s consider an example where a box is resting on a table. The weight of the box is 50 N, and the normal force exerted by the table is also 50 N in the opposite direction. Since these two forces are equal in magnitude but opposite in direction, the net force on the box is zero. In this case, the box remains in equilibrium and does not accelerate.

How to Determine the Magnitude and Direction of Net Force

Understanding the Concept of Direction in Physics

In physics, direction plays a vital role when considering forces. When forces act in the same direction, their magnitudes can be added to find the net force. However, when forces act in opposite directions, their magnitudes can be subtracted to determine the net force.

Steps to Determine the Direction of Net Force

To determine the direction of the net force, you can follow these steps:

1. Identify all the forces acting on the object.
2. Assign positive (+) or negative (-) signs to each force depending on their direction.
3. Add the magnitudes of the forces with the appropriate signs.
4. The resulting sign (+ or -) will indicate the direction of the net force.

Worked Out Example on Finding the Direction of Net Force

Let’s consider an example to understand how to find the direction of net force. Suppose an object is experiencing an applied force of 100 N in the positive x-direction and a frictional force of 50 N in the negative x-direction. To find the direction of the net force, we subtract the magnitude of the frictional force from the applied force:

 

Since the magnitude of the net force is positive, we can conclude that the net force is acting in the positive x-direction.

How to Calculate the Magnitude of Resultant Force

Understanding the Concept of Resultant Force

The resultant force is the single force that has the same effect as all the individual forces acting on an object. It represents the combined effect of multiple forces. To calculate the magnitude of the resultant force, we need to consider both the magnitude and direction of the individual forces.

The Mathematical Approach to Calculating Resultant Force

To calculate the magnitude of the resultant force, we can use vector addition. For two forces, (F_1) and (F_2), acting at an angle (theta) to each other, the formula for calculating the resultant force is:

Here, (cos(theta)) represents the cosine of the angle between the two forces.

Worked Out Example on Finding the Magnitude of Resultant Force

Let’s consider an example to illustrate how to calculate the magnitude of the resultant force. Suppose two forces, (F_1) and (F_2), are acting on an object at an angle of 60 degrees to each other. If (F_1) is 50 N and (F_2) is 30 N, we can calculate the magnitude of the resultant force using the formula mentioned earlier:

Simplifying the equation, we get:

Therefore, the magnitude of the resultant force is 80 N.

Remember, understanding the concepts, formulas, and steps to calculate net force, its direction, and resultant force is essential for solving physics problems effectively. By applying these principles, you can analyze the motion of objects and gain a deeper understanding of the forces at play. With practice and careful consideration, you’ll become more proficient at finding the magnitude of net force and interpreting its implications in various scenarios.

Quick Facts

Force being a vector quantity has both magnitude and direction. The measure or size of force acting on an object is known to be the magnitude of force.

The vector sum of forces that act on a body is the magnitude of resultant force. At a given time, there are always multiple forces working on a body. Either they act in the same direction or the opposite directions. The combination of all the forces keeps the object stable and does the work.

In physics, the single force that generates the same effect as multiple forces are known as the magnitude of the resultant force. Force, being a vector quantity, is important to consider the direction of a force. The forces that act in the same direction are taken as positive, and those acting in opposite directions are negative. The restaurant force is also known as the net force.

To understand the concept of the magnitude of resultant force, let us take a simple example.

Two to three people are required to lift a heavy box. But if there is an extremely strong bodybuilder, he can easily lift the box. Hence the force exerted by the bodybuilder would be almost equal to the force exerted by all the other people. And it would be the magnitude of resultant force

Numerically the resultant force is written as;

F = f₁ + f₂+ f₃

When the force on the body acts in the opposite direction, they are subtracted to generate the net force.

F = f₁ – f₂

When the force acts in a particular direction, they add up to get the magnitude of the resultant force.

F = f₁ + f₂

Classification of Resultant Force

The magnitude of the resultant force classifies it into;

• Balanced Force
• Unbalanced Force

Balanced Force

When the net force acting on a body equals zero, it is known as balanced force. Here forces are equal in magnitude but act in the opposite direction. If the force is balanced, the body will continue to remain in the position of rest or motion. There would be no acceleration.

Some instances of balanced force are;

In the above diagram, we can see that the weight of the body pulls it downwards, but due to the tension on the rope, it does not fall. Hence the magnitude of the resultant force acting on the body is zero.

Even the log floating on water is possible due to the balanced force. The weight of the log acts downwards, but the upthrust pulls it upwards. Hence the net force is zero, and the log floats on water. If the weight exceeds the upthrust, then the log will sink into the water.

A box resting on a table experiences a normal force that acts upwards and gravity downwards. Both the forces balance each other, and hence the magnitude of resultant force is zero.

Unbalanced Force

The unbalanced force has a magnitude not equal to zero. When the force acting in opposite or the same direction sums up generation acceleration, it is known to be the magnitude of the resultant force. The unbalanced force either moves a stationary object or changes the velocity of the body. The acceleration or change in a direction totally depends on the measure of the resultant force. Greater magnitude generates great deflection.

To understand the concept of an unbalanced force, look at these everyday activities;

The tug of war is the most basic instance of the resultant force. Once the two teams exert the same measure of force, but in opposite directions, no one moves. But the second any team generates more force than the other, the resultant force gets unbalanced, and they are able to pull the other team.

The moving car also experiences multiple forces. The engine applies a force that moves the car forward, but at the same time, the friction opposes its motion. Since the magnitude of the forward force is much greater than the friction force, it gets unbalanced. Hence the car moves towards the direction of restaurant force.

The apple falling on the ground is due to the magnitude of the resultant force. The gravity pulls the apple downwards, and the normal force acts upwards. But the strength of gravity is much greater than the normal force that the net force acts downwards.

Therefore, to sum up, the balanced and unbalanced force;

• Forces of equal magnitude acting in the opposite direction have resultant magnitude zero and no acceleration.
• Forces of unequal magnitude acting in opposite directions are subtracted, and the body accelerates towards the greater force.
• Force of unequal magnitude acting in the same direction adds up, and the body accelerates towards the resultant force.

Frequently Asked Question (FAQs)

What is the magnitude of force?

The external or internal strength acting on a body to bring necessary changes is known to be the force.

The measure of force is known as its magnitude. It is the numerical value that provides us with the idea of how much energy or strength is applied to do the work. For example, the force applied on the brake to stop the car is its magnitude.

What is the magnitude of resultant force?

The size or measure of force is known as the magnitude of force.

When two or more force acts on a body the total sum of the force that generates an effect on it, is known as the magnitude of resultant force. In simpler words, the sum of the total force is the resultant force. For example, when two people try to push the box in the same direction, their forces add up to generate resultant force. It helps them to push the box easily.

Are net force and resultant force equal?

The sum of all the forces acting on a body is known as resultant force.

The net force is the addition of the total force. Numerically it is the same as the resultant force. The net force is just the other name for the resultant force.

What happens when the magnitude of the resultant force is zero?

All the force acting on a body is added up to get the magnitude of resultant force.

When the magnitude of resultant force is zero, the body does not move, or there is no acceleration. The body remains in the same position of rest or motion. For example, the book kept on a table experiences normal force and gravitational pull. Both the forces are equal in magnitude and opposite in direction, and hence the resultant force adds up to zero.

How do balanced and unbalanced forces differ?

The resultant force is of two types; balanced and unbalanced force.

The balanced force has a net magnitude of zero, and the body does not accelerate. The unbalanced force has non-zero magnitude, and the body changes the velocity. When the cyclist rides a bicycle, he generates an unbalanced force that makes the cycle move. When he stops pedaling, the bicycle stops as the friction force and applied force gets balanced.

Is air resistance a balanced force?

The opposing force generated by the air on the moving body is air resistance.

To answer this question, let us take an example. When a ball falls downwards, it experiences air resistance and gravitational pull. The pull is of greater extent, and therefore the ball accelerates downwards. But there comes a time when the ball stops accelerating and just keeps falling down with the same velocity. It is at this time that the force becomes balanced.

How do unbalanced forces accelerate the body?

When the sum of force acting in the same or opposite direction is not zero, it is known as an unbalanced force.

When the net force is not zero, then there is some force acting on a body that will cause changes. Through a simple physics concept, we know that the body moves in the direction of greater magnitude. Hence the body changes velocity and accelerates towards the resultant force. It proves Newton’s First Law of Motion.

The magnitude of force refers to the strength or intensity of a force. It is a crucial concept in physics that helps us understand how objects interact with each other. The magnitude of force can be measured in various units, such as Newtons (N) or pounds (lbs). In this article, we will explore different examples of magnitude of force and how it affects the motion and behavior of objects. Understanding the magnitude of force is essential in fields like engineering, mechanics, and even everyday life situations. So, let’s dive in and explore some fascinating examples of the magnitude of force in action.

Key Takeaways

• The magnitude of force is a measure of the strength or intensity of a force.
• Examples of forces with large magnitudes include the force exerted by a rocket engine, the force of a car crashing into a wall, and the force exerted by a weightlifter lifting heavy weights.
• Forces with small magnitudes include the force exerted by a person pushing a door open, the force of gravity pulling an object downward, and the force of a pencil resting on a table.
• The magnitude of force can be calculated using Newton’s second law, which states that force is equal to mass multiplied by acceleration.

How to Find Magnitude of Force Examples

In the world around us, forces are constantly at play. From the gentle push of a breeze to the powerful pull of gravity, forces shape our everyday experiences. Understanding the magnitude of these forces is crucial in many fields, such as physics, engineering, and even sports. In this section, we will explore how to find magnitude of force examples by identifying everyday situations involving force, analyzing the forces involved in each situation, and determining the magnitude of force exerted in each situation.

Identifying Everyday Situations Involving Force

To begin our exploration of force examples, let’s take a moment to consider the various situations in which forces are at play. Forces can be found in countless scenarios, both big and small. Here are a few examples to help illustrate the point:

1. Throwing a Ball: When you throw a ball, you exert a force on it. The force you apply determines how far and how fast the ball will travel.

2. Lifting a Weight: When you lift a weight at the gym, you are exerting a force against the force of gravity. The heavier the weight, the greater the force required to lift it.

3. Driving a Car: When you press the accelerator pedal in a car, you apply a force that propels the vehicle forward. The force you exert determines how quickly the car accelerates.

4. Opening a Door: When you push or pull a door to open it, you apply a force to overcome the resistance of the door’s hinges and any friction present.

5. Jumping: When you jump, you exert a force against the ground, propelling yourself upward. The force you apply determines how high you can jump.

These examples highlight just a few everyday situations where forces are at play. By recognizing these scenarios, we can delve deeper into analyzing the forces involved.

Analyzing the Forces Involved in Each Situation

Now that we have identified some everyday situations involving force, let’s take a closer look at the forces at play in each scenario. By analyzing these forces, we can gain a better understanding of their magnitude. Let’s examine the forces involved in the examples mentioned earlier:

1. Throwing a Ball: When you throw a ball, several forces come into play. The force of your arm propels the ball forward, while gravity pulls it downward. Air resistance also acts upon the ball, opposing its motion through the air.

2. Lifting a Weight: When you lift a weight, the force you exert opposes the force of gravity pulling the weight downward. The magnitude of the force required depends on the weight of the object.

3. Driving a Car: When you press the accelerator pedal, the engine exerts a force that propels the car forward. Friction between the tires and the road also affects the force required to move the car.

4. Opening a Door: When you push or pull a door, the force you exert overcomes the resistance of the door’s hinges and any friction present. The force required depends on the weight and size of the door.

5. Jumping: When you jump, the force you apply to the ground propels you upward. Gravity acts as a downward force, opposing your upward motion. The force required to jump higher depends on factors such as leg strength and technique.

By analyzing the forces involved in each situation, we can now move on to determining the magnitude of force exerted.

Determining the Magnitude of Force Exerted in Each Situation

To determine the magnitude of force exerted in each situation, we need to consider the relevant factors and apply the appropriate formulas or calculations. Here are some ways to determine the magnitude of force in the examples we discussed:

1. Throwing a Ball: The magnitude of the force exerted when throwing a ball can be calculated using Newton’s second law of motion, which states that force equals mass multiplied by acceleration. By measuring the mass of the ball and the acceleration it experiences, we can determine the force exerted.

2. Lifting a Weight: The magnitude of the force required to lift a weight can be determined by measuring the weight of the object. The force exerted is equal to the weight of the object multiplied by the acceleration due to gravity.

3. Driving a Car: The magnitude of the force exerted when driving a car can be calculated by considering factors such as the mass of the car, the acceleration applied, and any resistive forces like friction. Newton’s second law of motion can be applied to determine the force exerted.

4. Opening a Door: The magnitude of the force required to open a door can be determined by considering factors such as the weight of the door, the distance from the hinges, and any friction present. By applying the principles of torque and equilibrium, we can calculate the force required.

5. Jumping: The magnitude of the force exerted when jumping can be determined by considering factors such as the mass of the person, the acceleration applied, and the height of the jump. Again, Newton’s second law of motion can be applied to calculate the force exerted.

By applying the appropriate formulas and calculations, we can determine the magnitude of force exerted in each situation. This knowledge is valuable in various fields and can help us better understand the world around us.

Magnitude of Force Examples

Pushing a Table

Pushing a table may seem like a simple task, but it involves various forces at play. When you push a table, you exert a force on it to overcome the force of static friction. Static friction is the force that prevents the table from moving when it is at rest.

Muscles in your body generate the necessary force to push the table. When you contract your muscles, they pull on your tendons, which in turn pull on your bones. This action creates a force that is transmitted to your hands, allowing you to exert force on the table. The magnitude of force you apply depends on factors such as the weight of the table and the coefficient of friction between the table and the floor.

Friction plays a crucial role in determining the magnitude of force required to push the table. If the coefficient of friction is high, it will be more challenging to move the table, and you will need to apply a greater force. On the other hand, if the coefficient of friction is low, it will be easier to push the table, and a smaller force will be sufficient.

Lifting a Box

Lifting a box off the ground involves overcoming the force of gravity. When you lift a box, you exert an upward force that counteracts the downward force of gravity. This force is generated by the muscles in your body.

Your muscles contract, pulling on your tendons and bones, which allows you to generate the necessary force to lift the box. The magnitude of force required depends on the weight of the box. Heavier boxes require a greater force to lift, while lighter boxes require less force.

Drawing Water from a Well

Drawing water from a well often involves the use of ropes and pulleys to exert force. When you pull on the rope, the force is transmitted through the rope to the pulley system. The pulleys multiply the force, making it easier to lift the water.

The magnitude of force required to draw water from a well depends on various factors, such as the weight of the water and the efficiency of the pulley system. A well-designed pulley system can significantly reduce the force needed to lift the water.

Swimming in a Pool

Swimming in a pool involves experiencing several forces. One of these forces is buoyant force, which acts in the upward direction and counteracts the weight of your body. Buoyant force allows you to float in the water.

To move forward while swimming, you need to overcome fluid friction. When you move your arms and legs, you generate a force that propels you through the water. The magnitude of force required to swim depends on factors such as your body size, swimming technique, and the resistance offered by the water.

Playing Cricket

Cricket involves various forces that come into play during the game. When a bowler throws the ball, it experiences the force of air resistance. Air resistance acts in the opposite direction to the ball’s motion, slowing it down.

To hit the ball, a batsman needs to generate a force with the cricket bat. The magnitude of force required depends on factors such as the speed and trajectory of the ball, as well as the desired distance and direction of the hit.

Riding a Bicycle

Riding a bicycle involves the application of force to move forward. When you pedal, you convert the energy from your muscles into kinetic energy, propelling the bicycle forward. The force you apply to the pedals is transmitted through the chain to the wheels, causing them to rotate.

Friction plays a crucial role in maintaining speed and starting the bike. The force of friction between the tires and the road allows the bike to grip the surface and move forward. Without friction, it would be challenging to ride a bicycle.

Squeezing a Lemon

Squeezing a lemon involves applying force to extract the juice. When you squeeze the lemon, you apply a muscular force to compress it. This force causes the lemon to deform, releasing the juice contained within.

The magnitude of force required to squeeze a lemon depends on factors such as the ripeness of the fruit and the desired amount of juice. Ripe lemons are easier to squeeze, requiring less force, while unripe lemons may require more force to extract the juice.

Applying Brake to a Vehicle

Applying the brake to a vehicle involves the generation of friction force to stop its motion. When you press the brake pedal, it activates the brake system, which applies friction to the wheels. This friction force opposes the vehicle‘s motion, eventually bringing it to a stop.

The magnitude of force required to stop a vehicle depends on factors such as its speed, mass, and the efficiency of the braking system. Higher speeds and heavier vehicles require a greater force to stop within a given distance.

Towing a Car

When it comes to towing a car, there are various forces at play that allow for the successful movement of one vehicle by another. Let’s take a closer look at the different aspects involved in this process.

Description of the Force Involved in Towing

Towing a car requires the application of a force known as tension force. This force is exerted on the tow bar, which is connected to both the towing vehicle and the car being towed. The tension force acts in the direction of the tow, allowing the towing vehicle to pull the other car along.

Role of Tension Force in Accelerating the Vehicles

The tension force plays a crucial role in accelerating both the towing vehicle and the car being towed. As the towing vehicle exerts a force on the tow bar, the tension force transfers this force to the car being towed. This transfer of force causes the car to accelerate and move in the same direction as the towing vehicle.

Balancing Tension Force on the Tow Bar

To ensure a smooth and safe towing experience, it is important to maintain a balanced tension force on the tow bar. If the tension force is too high, it can lead to excessive strain on the tow bar and potentially cause damage. On the other hand, if the tension force is too low, the car being towed may not move effectively. Finding the right balance is crucial for a successful towing operation.

Frequently Asked Questions

Q1: What is the magnitude of force?

The magnitude of force refers to the size or strength of a force. It is a scalar quantity that represents the amount of push or pull exerted on an object.

Q2: How can I find the magnitude of a force?

To find the magnitude of a force, you can use the formula: magnitude = mass × acceleration. This formula applies to forces acting in a straight line.

Q3: Can you provide some examples of force magnitude?

Certainly! Here are a few examples of force magnitude:

• Pushing a car with a force of 500 Newtons.
• Pulling a suitcase with a force of 50 Newtons.
• Lifting a weight with a force of 1000 Newtons.

Q4: Are there any illustrations or demonstrations of force magnitude?

Yes, there are various ways to illustrate or demonstrate force magnitude. For example, you can use a spring scale to measure the force required to stretch or compress a spring. Another demonstration involves using a force sensor to measure the force exerted by an object.

Q5: Can you provide some instances or cases of force magnitude?

Certainly! Here are a few instances or cases of force magnitude:

• Calculating the force required to accelerate a rocket into space.
• Determining the force needed to lift a heavy object.
• Measuring the force exerted by a person while pushing a shopping cart.

Q6: How can I find the magnitude and direction of a resultant force?

To find the magnitude and direction of a resultant force, you can use vector addition. This involves adding the individual forces together using the rules of vector addition. The magnitude of the resultant force can be found using the Pythagorean theorem, and the direction can be determined using trigonometry.

Q7: Are there any examples of magnitude and direction of resultant force?

Certainly! Here are a few examples of magnitude and direction of resultant force:

• Two forces of 10 Newtons and 15 Newtons acting at an angle of 30 degrees to each other.
• Three forces of 20 Newtons, 30 Newtons, and 40 Newtons acting at different angles to each other.

Q8: Can you provide some force magnitude exemplifications?

Certainly! Here are a few force magnitude exemplifications:

• Calculating the force required to stop a moving car.
• Determining the force needed to launch a rocket into orbit.
• Measuring the force exerted by a person while lifting weights.

Q9: Are there any force magnitude representations?

Yes, there are various ways to represent force magnitude. One common representation is using vector diagrams, where the length of the arrow represents the magnitude of the force. Another representation is using numerical values with appropriate units, such as Newtons (N) or pounds (lb).

Q10: Can you provide some force magnitude samples?

Certainly! Here are a few force magnitude samples:

• Calculating the force required to move a heavy object across a frictional surface.
• Determining the force needed to stretch a spring to a certain length.
• Measuring the force exerted by a person while rowing a boat.

Force can be classified as internal or external forces. We will be discussing the types of the latter, one that is an external force.

The external force is exerted between the body and the surrounding. It occurs when the force is applied to any object from outside and is non-conservative. The change in velocity is the basic effect caused by external forces. The types of external forces are:

• Friction Force
• Normal Force
• Air Resistance Force
• Applied Force
• Tension

Friction force

When an object moves over a surface, then a restricting force emerges that tries to oppose the motion of the body. This force is known as the Force of Friction or Frictional Force. Some of the kinetic energy of the body is converted into heat energy to obstruct the motion and get lost. Hence frictional force is non-conservative.

The basic example of friction is the lightning of a matchstick. When we rub the stick on the surface, friction comes into play and converts kinetic energy into heat that ignites the matchstick. Friction also helps us to walk and write.

The friction force is dependent on the factors; normal force and a coefficient of friction µ.

The straightforward formula for friction is:

Where,

N is the normal force acting perpendicularly to the surface

µ is the coefficient of friction, and its value completely depends on the surface.

The frictional force can be classified into given four categories:

• Static Friction
• Sliding Friction
• Rolling Friction
• Fluid Friction

Normal Force

The normal force acts on every object perpendicularly to keep them from falling off and at a stable position. It only comes into the act when the body and surface are in contact with each other. For example, a book lying on a table experiences gravitational force downwards but does not fall. The normal force pulls upwards to keep it off from falling. It is generated by the surface of the object. Every object, even humans too, experiences the normal force, and it is a non-conservative force.

From the diagram we can see:

Where,

N is the normal force

m is the mass of the body

g is the acceleration due to gravity.

From the free-body diagram:

On splitting W into two components, we get:

Here,

N = normal force

m = mass

g = acceleration due to gravity

Θ = angle between the inclined surface

Air Resistance Force

The external force caused by the body flying or moving through the air is known as air resistance force or air drag. It acts in the opposing direction of the motion of the object.  The resistance is also caused due to the collision of air molecules and the object’s surface. Hence, this force depends on two factors; the velocity of the moving body and the area of the object. That is why all the aircraft and birds have a streamlined front to reduce the area, which leads to less air resistance force and hence their easy movement. 

The force of air resistance is given as:

Here,

F_air = air resistance force

c = force constant

v = velocity of the object

The negative sign indicates that the direction of the force air resistance is opposite to the motion of the object.

Applied Force

The simple external push and pull force that is applied to the object is applied force. It tends to move the body at rest or change the velocity of the moving body. The applied force can be classified into contact and non-contact forces. The contact force is the type of external force. The applied force can be differentiated as:

• Pull: When the force is applied to move the object towards oneself. Example: Pulling the rope

• Push: When the force is applied in such a way to move the object in the forward direction and away from oneself. Example: Pushing the box.

• Collision: when two bodies collide with each other, they both exert force on each other. The collision tends to change the velocity and direction of the collided bodies. The collision can be elastic and inelastic.

According to the second law of motion, the formula of applied force is:

Where,

F = applied force

m = mass of the body

a = acceleration produced.

Tension

When a load is attached to any kind of string, cable, rope, or similar object, a pulling force is exerted along the length of the object in the upward direction. In physics, this force is known as tension. It is important to remember that tension does not apply on its own; it has to be provided to the system. While explaining the concept of tension force, we take the string to be massless so that the applied tension is equally transmitted to the whole string. Some of the examples of tension force are:

• Tug of war
• Towing of car
• Pulling a box with the help of a rope.

From the free diagram, the formula for tension can be determined as:

Where,

T= tension force

m=mass of the body

g= acceleration due to gravity

Types of Friction Force

Static Friction

Static friction comes into play when the body and the surface area are at the rest position with respect to each other. This force helps the object to avoid any trigger caused by applied forces. The object only comes into motion when the applied force exceeds the static force.

The basic example of static friction is pushing a heavy box. The static friction does not allow the motion of the box. It is only when two or three people come together and apply greater force than the static friction that the box moves. 

Other examples are:

• Book on a table
• Clothes hanging on the rack
• A car parked on a hill

The value of static friction is calculated from the formula:

To move the object, the inequation is given as:

Here,

F_s is the static friction

µ_s is the coefficient of static friction

N is the normal force acting perpendicularly to the surface

Sliding friction

When an object slides over another body or surface, then the opposition that is created against the motion is known as the sliding friction.

An example of sliding friction is ice skating. When a person pushes the ice skate forward by applying their weight, sliding friction is created. It generates the heat energy that melts the ice and helps in sliding the skate easily.

More example of sliding friction is:

• Sliding book over the table
• Rubbing of rag on the counter
• Sliding through a slide
• Sliding car on the ramp

The formula for sliding friction is given as:

Here,

F_s = sliding friction

µ_s = coefficient of sliding friction

N = normal force

Rolling friction

The friction that acts on a body when it rolls over a surface is known as rolling friction or rolling drag. When an object rolls over a surface, both of them get deformed at the point of contact that tends to create motion below the surface.

It is due to the rolling friction that a rolling ball stops after some time. Without friction, the ball would keep rolling forever. Other examples of rolling friction are:

• The wheels of all the vehicles generate rolling friction
• Rolling of pencil

The formula for rolling friction is:

Where,

F_r is the rolling friction

µ_r is the coefficient of rolling friction

N is the normal force

Fluid friction

Friction not only opposes the movement of solid objects. The layers of liquid when slide against each other, friction is generated between them known as fluid friction. It also restricts the movement of other objects into the liquid.

The fluid friction restrains the movement of swimmers, and hence it requires much energy for swimming in water. Also, the water gushing around their body is due to fluid friction. The other examples of this friction are:

• Stirring of a spoon into coffee or milk
• Movement of the submarine through the water.

Frequently Asked Question (FAQs)

What is external force?

A body can experience a force in two ways externally and internally. 

The force exerted from outside on any object is known to be an external force. It can be a contact force as well as a non-contact force. Mostly external force is contact force and comes into action when an object interacts with its surroundings. Pushing a table and car are some examples of external force. 

Is external force conservative or non-conservative?

The conservation of energy classifies the force as conservative and non-conservative. 

When an object experiences the external force, energy is generated, and work is done on it. In doing the work, some of the energy gets dissipated. Hence the total energy before and after the force is applied does not remain the same. Therefore, an external force is non-conservative. 

What are the types of external force?

The external force is of the following five types:

• Friction
• Tension
• Normal force
• Air resistance 
• An applied force. 

What are the effects of external force?

The external force generally tends to change the velocity of the moving body. 

What are the advantages of friction?

The opposing force acting on a moving object is called friction.  

Friction is a necessary phenomenon that makes our everyday work easier. When we walk on the ground, the friction caused by the ground on our feet helps in walking by pushing us forward. It also helps us to write, in skiing and many other things. 

How can friction be of disadvantage?

Friction makes our everyday work possible, but it also causes some damage.

The opposition generated on the moving body by friction is done by converting kinetic energy into heat energy. The heat causes unnecessary wear and tear of objects and also reduces the working efficiency of the machines. In order to subdue the friction, a lot of energy is required.