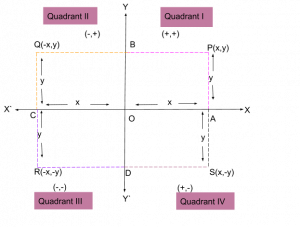
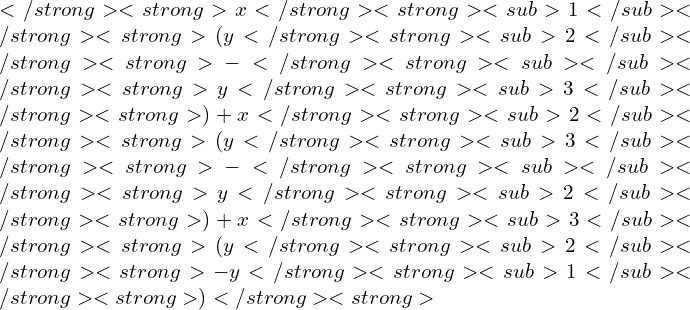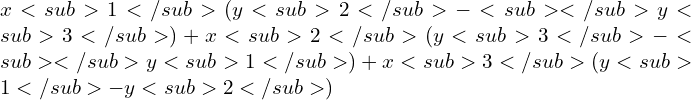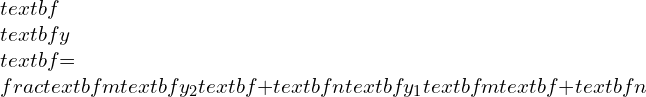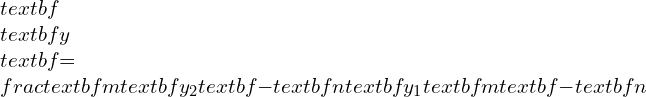2D Coordinate Geometry: 11 Important Facts

December 31, 2023July 24, 2021 by NASRINA PARVIN

Locus in 2D Coordinate Geometry

Locus is a Latin word. It is derived from the word ‘Place’ or ‘Location’. The Plural of locus is Loci.

Definition of Locus:

In Geometry, ‘Locus’ is a set of points which satisfy one or more specified conditions of a figure or shape. In modern mathematics, the location or the path on which a point moves on the plane satisfying given geometrical conditions, is called locus of the point.

Locus is defined for line, line segment and the regular or irregular curved shapes except the shapes having vertex or angles inside them in Geometry. https://en.wikipedia.org/wiki/Coordinate_system

Examples on Locus:

lines, circles, ellipse, parabola, hyperbola etc. all these geometrical shapes are defined by the locus of points.

Equation of the Locus:

The algebraic form of the geometrical properties or conditions which are satisfied by the coordinates of all the points on Locus, is known as the equation of the locus of those points.

Method of Obtaining the Equation of the Locus:

To find the equation of the locus of a moving point on a plane, follow the process described below

(i) First, assume the coordinates of a moving point on a plane be (h,k).

(ii) Second, derive a algebraic equation with h and k from the given geometrical conditions or properties.

(iii) Third, replace h and k by x and y respectively in the above said equation. Now this equation is called the the equation of the locus of the moving point on the plane. (x,y) is the current coordinates of the moving point and the equation of the locus must always be derived in the form of x and y i.e. current coordinates.

Here are some examples to make the conception clear about locus.

4+different types of solved problems on Locus:

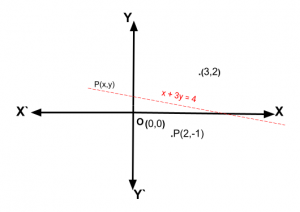
Problem 1: If P be any point on the XY-plane which is equidistant from two given points A(3,2) and B(2,-1) on the same plane, then find the locus and the equation of locus of the point P with graph.

Solution:

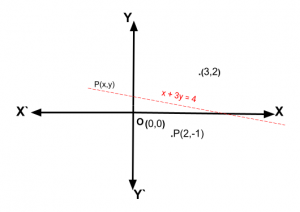
Assume that the coordinates of any point on the locus of P on XY-plane are (h, k).

Since, P is equidistant from A and B, we can write

The distance of P from A=The distance of P from B

Or, |PA|=|PB|

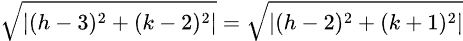
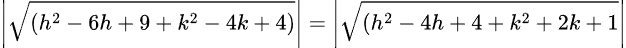
Or, (h² -6h+9+k² -4k+4) = (h² -4h+4+k² +2k+1)——– taking square to both sides.

Or, h² -6h+13+k² -4k -h²+4h-5-k² -2k = 0

Or, -2h -6k+8 = 0

Or, h+3k -4 = 0

Or, h+3k = 4 ——– (1)

This is a first degree equation of h and k.

Now if h and k are replaced by x and y then the equation (1) becomes the first degree equation of x and y in the form of x + 3y = 4 which represents a straight line.

Therefore, the locus of the point P(h, k) on XY-plane is a straight line and the equation of the locus is x + 3y = 4 . (Ans.)

Problem 2: If a point R moves on the XY-plane in such way that RA : RB = 3:2 where the coordinates of the points A and B are (-5,3) and (2,4) respectively on the same plane, then find the locus of the point R.

What type of curve does the equation of the locus of R indicate?

Solution: Lets assume that the coordinates of any point on the locus of given point R on XY-plane be (m, n).

Asper given condition RA : RB = 3:2,

we have,

(The distance of R from A) / (The distance of R from B) = 3/2

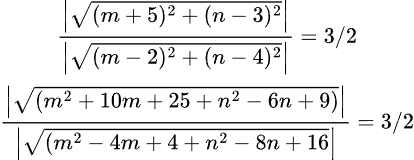
Or, (m² +10m+34+n² -6n) / (m² -4m+n² -8n+20) =9/4 ———– taking square to both sides.

Or, 4(m² +10m+34+n² -6n) = 9(m² -4m+n² -8n+20)

Or, 4m² +40m+136+4n² -24n = 9m² -36m+9n² -72n+180)

Or, 4m² +40m+136+4n² -24n – 9m² +36m-9n² +72n-180 = 0

Or, -5m² +76m-5n²+48n-44 = 0

Or, 5(m²+n²)-76m+48n+44 = 0 ———-(1)

This is a second degree equation of m and n .

Now if m and n are replaced by x and y, the equation (1) becomes the second degree equation of x and y in the form of 5(x²+y²)-76x+48y+44 = 0 where the coefficients of x² and y² are same and the coefficient of xy is zero. This equation represents a circle.

Therefore, the locus of the point R(m, n) on XY-plane is a circle and the equation of the locus is

5(x²+y²)-76x+48y+44 = 0 (Ans.)

Problem 3: For all values of (θ,aCosθ,bSinθ) are the coordinates a point P which moves on the XY plane. Find the equation of locus of P.

Solution: lets (h, k) be the coordinates of any point lying on the locus of P on XY-plane.

Then asper the question, we can say

h= a Cosθ

Or, h/a = Cosθ —————(1)

And k = b Sinθ

Or, k/b = Sinθ —————(2)

Now taking square of both the equations (1) and (2) and then adding, we have the equation

h²/a² + k²/b² =Cos²θ + Sin²θ

Or, h²/a² + k²/b² = 1 (Since Cos²θ + Sin²θ =1 in trigonometry)

Therefore the equation of locus of the point P is x²/a² + y²/b² = 1 . (Ans.)

Problem 4 : Find the equation of locus of a point Q, moving on the XY-plane, if the coordinates of Q are

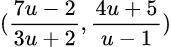
where u is the variable parameter.

Solution : Let the coordinates of any point on the locus of given point Q while moving on XY-plane be (h, k).

Then, h = and k =

i.e. h(3u+2) = 7u-2 and k(u-1) = 4u+5

i.e. (3h-7)u = -2h-2 and (k-4)u = 5+k

i.e. u =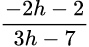 —————(1)

and u = —————(2)

Now equating the equations (1) and (2) , we get,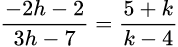

Or, (-2h-2)(k-4) = (3h-7)(5+k)

Or, -2hk+8h-2k+8 = 15h+3hk-35-7k

Or, -2hk+8h-2k-15h-3hk+7k = -35-8

Or, -5hk-7h+5k = -43

Or, 5hk+7h-5k = 43

Therefore, the equation of the locus of Q is 5xy+7x-5y = 43.

Basic Examples on the Formulae “Centroid of a Triangle” in 2D Coordinate Geometry

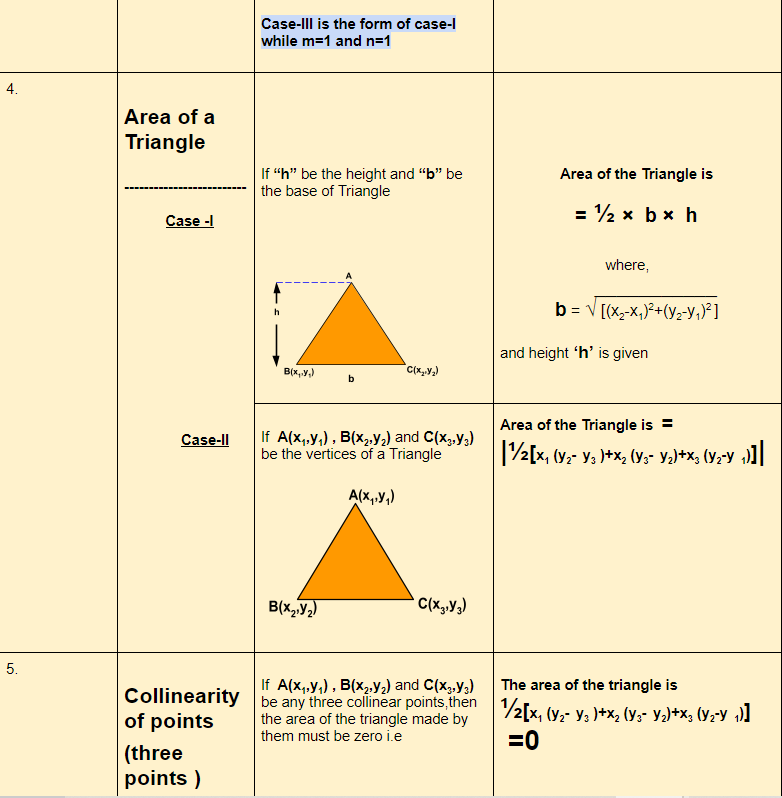
Centroid: The three medians of a triangle always intersect at a point, located in the interior area of the triangle and divides the median at the ratio 2:1 from any vertex to the midpoint of the opposite side. This point is called the centroid of the triangle.

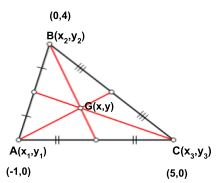
Problems 1: Find the centroid of the triangle with vertices (-1,0), (0,4) and (5,0).

Solution: We already know,

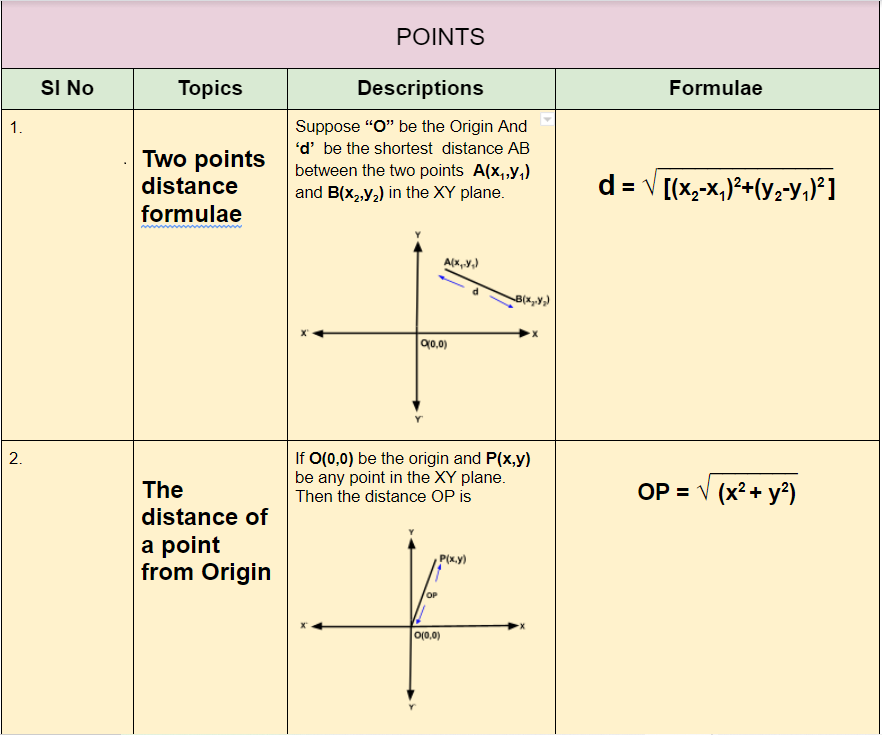
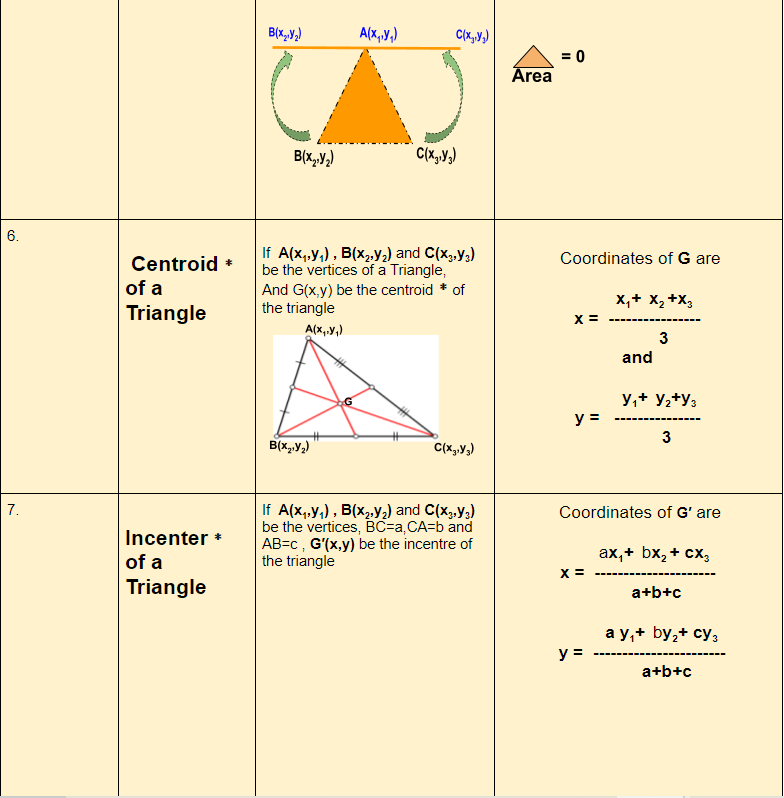
If A(x₁,y₁) , B(x₂,y₂) and C(x₃,y₃) be the vertices of a Triangle and G(x, y) be the centroid of the triangle, then Coordinates of G are

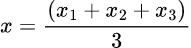
and

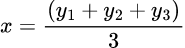
Using this formula we have ,

(x₁,y₁) ≌(-1,0) i.e. x₁= -1, y₁=0 ;

(x₂,y₂) ≌(0,4) i.e. x₂=0, y₂=4 and

(x₃,y₃) ≌(5,0) i.e. x₃=5, y₃=0

(See formulae chart)

Screenshot 17 — **Graphical Representation**

So, the x-coordinate of the centroid G,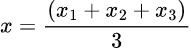

i.e.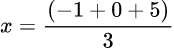

i.e. x=4/3

and

the y-coordinate of the centroid G,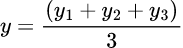

i.e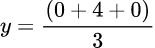

i.e y=4/3

Therefore, the coordinates of the centroid of the given triangle is 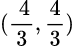. (Ans)

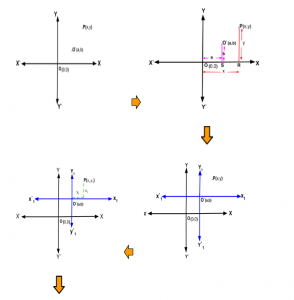
Shifting of Origin / Translation of Axes- 2D Co-ordinate Geometry

Shifting of Origin means to shift the Origin to a new point keeping the orientation of the axes unchanged i.e the new axes remain parallel to the original axes in the same plane. By this translation of axes or shifting of origin process many problems on algebraic equation of a geometric shape are simplified and solved easily.

The formula of ” Shifting of Origin” or “Translation of Axes” are described below with graphical representation.

Formula:

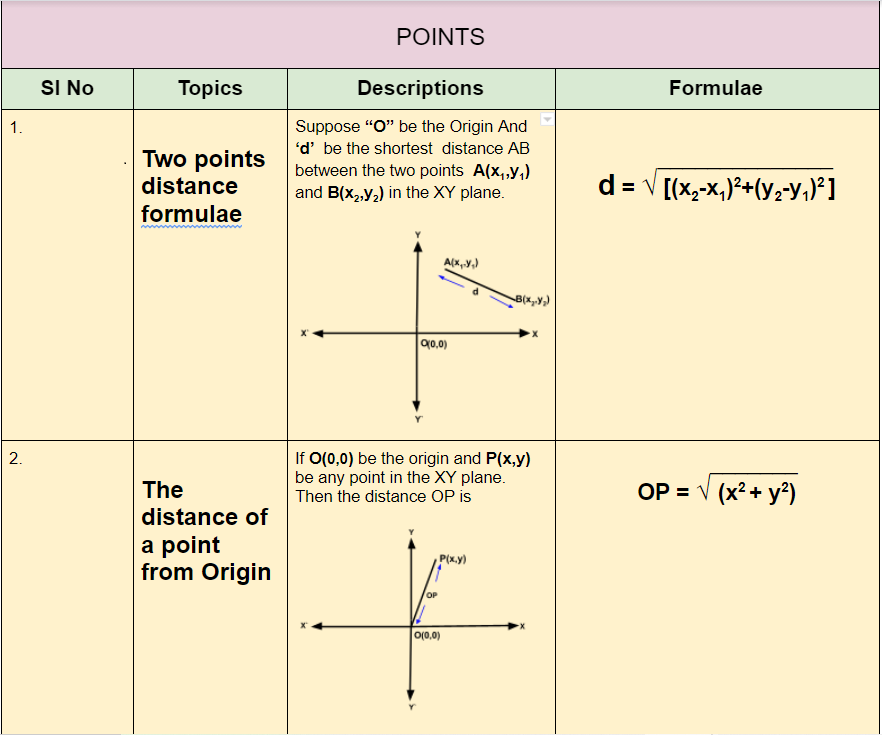
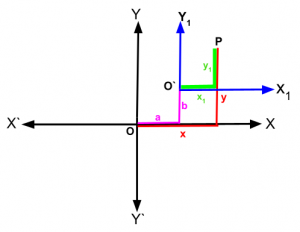
If O be the origin ,P(x,y) be any point in the XY plane and O be shifted to another point O′(a,b) against which the coordinates of the point P become (x₁,y₁) in the same plane with new axes X₁Y₁ ,Then New Coordinates of P are

x₁= x- a

y₁ = y- b

Graphical representation for clarification: Follow the graphs

Few solved Problems on the formula of ‘Shifting of Origin’ :

Problem-1 : If there are two points (3,1) and (5,4) in the same plane and the origin is shifted to the point (3,1) keeping the new axes parallel to the original axes, then find the co-ordinates of the point (5,4) in respect with the new origin and axes.

Solution: Comparing with the formula of ‘Shifting of Origin’ described above , we have new Origin, O′(a, b) ≌ (3,1) i.e. a=3 , b=1 and the required point P, (x, y) ≌ (5,4) i.e. x=5 , y=4

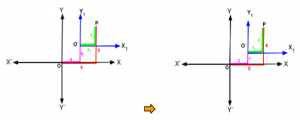
Now if (x₁,y₁) be the new coordinates of the point P(5,4) ,then asper formula x₁ = x-a and y₁ =y-b,

we get, x₁ = 5-3 and y₁ =4-1

i.e. x₁ = 2 and y₁ =3

Therefore, the required new coordinates of the point (5,4) is (2,3) . (Ans.)

Problem-2 : After shifting the Origin to a point in the same plane ,remaining the axes parallel to each other ,the coordinates of a point (5,-4) become (4,-5).Find the Coordinates of new Origin.

Solution: Here using the formula of ‘Shifting the Origin’ or ‘Translation of Axes’ , we can say the coordinates of the point P with respect to old and new Origin and axes respectively are (x, y) ≌ (5,-4) i.e. x=5 , y= -4 and (x₁,y₁) ≌ (4,-5) i.e. x₁= 4, y₁= -5

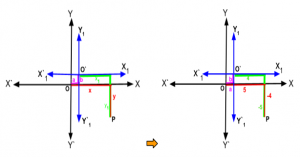
Now we have to find the coordinates of the new Origin O′(a, b) i.e. a=?, b=?

Asper formula,

x₁= x- a

y₁ = y- b

i.e. a=x-x₁ and b=y-y₁

Or, a=5-4 and b= -4-(-5)

Or, a=1 and b= -4+5

Or, a=1 and b= 1

Therefore, O'(1,1) be the new Origin i.e. the coordinates of the new Origin are (1,1). (Ans.)

Basic Examples on the Formulae “Collinearity of points (three points)” in 2D Coordinate Geometry

Problems 1: Check whether the points (1,0), (0,0) and (-1,0) are collinear or not.

Solution: We already know,

If A(x₁,y₁) , B(x₂,y₂) and C(x₃,y₃) be any three collinear points, then the area of the triangle made by them must be zero i.e the area of the triangle is ½[x₁ (y₂– y₃) + x₂ (y₃– y₁) + x₃ (y₁-y₂)] =0

(See formulae chart)

Using this formula we have ,

(x₁,y₁) ≌(-1,0) i.e. x₁= -1, y₁= 0 ;

(x₂,y₂) ≌(0,0) i.e. x₂= 0, y₂= 0;

(x₃,y₃) ≌(1,0) i.e. x₃= 1, y₃= 0

Screenshot 14 — **Graphical Representation**

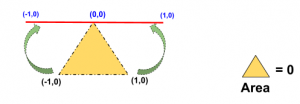
So, the area of the triangle is = |½[x₁ (y₂– y₃) + x₂ (y₃– y₁) + x₃ (y₁-y₂)]| i.e.

(L.H.S) = |½[-1 (0-0) + 0 (0-0) + 1 (0-0)]|

= |½[(- 1)x0 + 0x0 + 1×0]|

= |½[0 + 0 + 0]|

= |½ x 0|

= 0 (R.H.S)

Therefore, the area of the triangle made by those given points become zero which means they are lying on the same line.

Therefore, the given points are collinear points. (Ans)

Basic Examples on the Formulae “Incenter of a Triangle” in 2D Coordinate Geometry

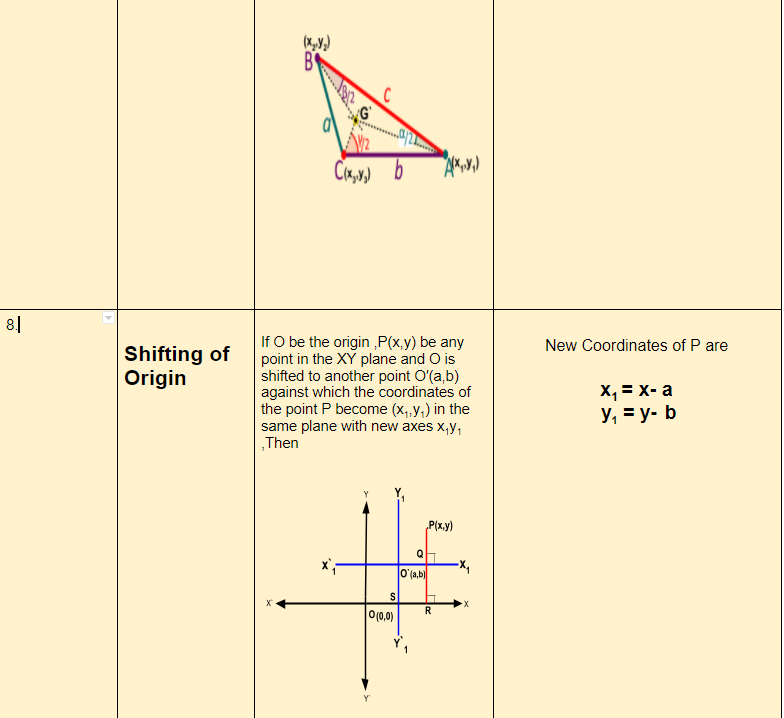
Incenter:It is the center of the triangle’s largest incircle which fits inside the triangle.It is also the point of intersection of the three bisectors of the interior angles of the triangle.

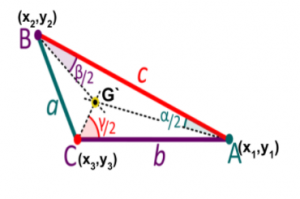
Problems 1: The vertices of a triangle with sides are (-2,0), (0,5) and (6,0) respectively. Find the incenter of the triangle.

Solution: We already know,

If A(x₁,y₁) , B(x₂,y₂) and C(x₃,y₃) be the vertices, BC=a, CA=b and AB=c , G′(x,y) be the incentre of the triangle,

The co-ordinates of G′ are

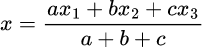
and

(See formulae chart)

Asper the formula we have,

(x₁,y₁) ≌(-4,0) i.e. x₁= -4, y₁=0 ;

(x₂,y₂) ≌(0,3) i.e. x₂=0, y₂=3 ;

(x₃,y₃) ≌(0,0) i.e. x₃=0, y₃=0

We have now,

a= √ [(x₂-x₁)²+(y₂-y₁)²]

Or, a= √ [(0+4)²+(3-0)²]

Or, a= √ [(4)²+(3)²]

Or, a= √ (16+9)

Or, a= √25

Or, a = 5 ——————(1)

b=√ [(x₁-x₃)²+(y₁-y₃)²]

Or, b= √ [(-4-0)²+(0-0)²]

Or, b= √ [(-4)²+(0)²]

Or, b= √ (16+0)

Or, b= √16

Or, b= 4 ——————–(2)

c= √ [(x₃-x₂)²+(y₃-y₂)²]

Or, c= √ [(0-0)²+(0-3)²]

Or, c= √ [(0)²+(-3)²]

Or, c= √ (0+9)

Or, c= √9

Or, c= 3 ——————–(3)

and ax₁+ bx₂+ cx₃ = (5 X (-4)) + (4 X 0) + (3 X 6 )

= -20+0+18

Or, ax₁+ bx₂+ cx₃ = -2 ——————-(4)

ay₁+ by₂+ cy₃ = (5 X 0) + (4 X 3) + (3 X 0)

= 0+12+0

Or, ay₁+ by₂+ cy₃ = 12 ——————–(5)

a+b+c = 5+4+3

Or, a+b+c = 12 ——————(6)

Using the above equations (1), (2), (3), (4), (5) and (6) we can calculate the value of x and y from

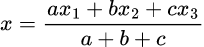
Or, x = -2/12

Or, x = -1/6

and

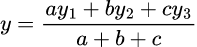
Or, y = 12/12

Or, y = 1

Therefore the required coordinates of the incenter of the given triangle are (-1/6 , 1). (Ans.)

Point Sections Or Ratio Formulae: 41 Critical Solutions

October 6, 2023July 7, 2021 by NASRINA PARVIN

Basic Examples on the Formulae “Point sections or Ratio”

Case-I

Problems 21: Find the coordinates of the point P(x, y) which internally divides the line segment joining the two points (1,1) and (4,1) in the ratio 1:2.

Solution: We already know,

If a point P(x, y) divides the line segment AB internally in the ratio m:n,where coordinates of A and B are (x₁,y₁) and (x₂,y₂) respectively. Then Coordinates of P are

and

(See formulae chart)

Using this formula we can say , (x₁,y₁) ≌(1,1) i.e. x₁=1, y₁=1 ;

(x₂,y₂)≌(4,1) i.e. x₂=4, y₂=1

and

m:n ≌ 1:2 i.e m=1,n=2

Therefore,

x =

( putting values of m & n in

Or, x =1*4+2*1/3 ( putting values of x₁ & x₂ too )

Or, x = 4+2/3

Or, x = 6*3

Or, x = 2

Similarly we get,

y =

( putting values of m & n in y =

Or, y =(1*1+2*1)/3 ( putting values of y₁ & y₂ too )

Or, y = 1*1+2/3

Or, y = 3/3

Or, y = 1

Therefore, x=2 and y=1 are the coordinates of the point P i.e. (2,1). (Ans)

More answered problems are given below for further practice using the procedure described in above problem 21:-

Problem 22: Find the coordinates of the point which internally divides the line segment joining the two points (0,5) and (0,0) in the ratio 2:3.

Ans. (0,2)

Problem 23: Find the point which internally divides the line segment joining the points (1,1) and (4,1) in the ratio 2:1.

Ans. (3,1)

Problem 24: Find the point which lies on the line segment joining the two points (3,5,) and (3,-5,) dividing it in the ratio 1:1

Ans. (3,0)

Problem 25: Find the coordinates of the point which internally divides the line segment joining the two points (-4,1) and (4,1) in the ratio 3:5

Ans. (-1,1)

Problem 26: Find the point which internally divides the line segment joining the two points (-10,2) and (10,2) in the ratio 1.5 : 2.5.

_____________________________

Case-II

Problems 27: Find the coordinates of the point Q(x,y) which externally divides the line segment joining the two points (2,1) and (6,1) in the ratio 3:1.

Solution: We already know,

If a point Q(x,y) divides the line segment AB externally in the ratio m:n,where coordinates of A and B are (x₁,y₁) and (x₂,y₂) respectively,then the coordinates of the point P are

and

(See formulae chart)

Using this formula we can say , (x₁,y₁) ≌(2,1) i.e. x₁=2, y₁=1 ;

(x₂,y₂)≌(6,1) i.e. x₂=6, y₂=1 and

m:n ≌ 3:1 i.e. m=3,n=1

Point sections — Graphical Representation

Therefore,

x =

( putting values of m & n in x =

Or, x =(3*6)-(1*2)/2 ( putting values of x₁ & x₂ too )

Or, x = 18-2/2

Or, x =16/2

Or, x = 8

Similarly we get,

y =

( putting values of m & n in y =

Or, y =

( putting values of y₁ & y₂ too )

Or, y = 3-1/2

Or, y = 2/2

Or, y = 1

Therefore, x=8 and y=1 are the coordinates of the point Q i.e. (8,1). (Ans)

More answered problems are given below for further practice using the procedure described in above problem 27:-

Problem 28: Find the point which externally divides the line segment joining the two points (2,2) and (4,2) in the ratio 3 : 1.

Ans. (5,2)

Problem 29: Find the point which externally divides the line segment joining the two points (0,2) and (0,5) in the ratio 5:2.

Ans. (0,7)

Problem 30: Find the point which lies on the extended part of the line segment joining the two points (-3,-2) and (3,-2) in the ratio 2 : 1.

Ans. (9,-2)

________________________________

Case-III

Problems 31: Find the coordinates of the midpoint of the line segment joining the two points (-1,2) and (1,2).

Solution: We already know,

If a point R(x,y) be the midpoint of the line segment joining A(x₁,y₁) and B(x₂,y₂) .Then coordinates of R are

and

(See formulae chart)

Case-III is the form of case-I while m=1 and n=1

Using this formula we can say , (x₁,y₁) ≌(-1,2) i.e. x₁=-1, y₁=2 and

(x₂,y₂)≌(1,2) i.e. x₂=1, y₂=2

Screenshot 11 — Graphical Representation

Therefore,

x =

( putting values of x₁ & x₂ in x =

Or, x = 0/2

Or, x = 0

Similarly we get,

y =2+2/2 ( putting values of y₁ & y₂ in y =

Or, y = 4/2

Or, y = 2

Therefore, x=0 and y=2 are the coordinates of the midpoint R i.e. (0,2). (Ans)

More answered problems are given below for further practice using the procedure described in above problem 31:-

Problem 32: Find the coordinates of the midpoint of the line joining the two points (-1,-3) and (1,-4).

Ans. (0,3.5)

Problem 33: Find the coordinates of the midpoint which divides the line segment joining the two points (-5,-7) and (5,7).

Ans. (0,0)

Problem 34: Find the coordinates of the midpoint which divides the line segment joining the two points (10,-5) and (-7,2).

Ans. (1.5, -1.5)

Problem 35: Find the coordinates of the midpoint which divides the line segment joining the two points (3,√2) and (1,3√2).

Ans. (2,2√2)

Problem 36: Find the coordinates of the midpoint which divides the line segment joining the two points (2+3i,5) and (2-3i,-5).

Ans. (2,0)

Note: How to check if a point divides a line (length=d units) internally or externally by the ratio m:n

If ( m×d)/(m+n) + ( n×d)/(m+n) = d , then internally dividing and

If ( m×d)/(m+n) – ( n×d)/(m+n) = d , then externally dividing

____________________________________________________________________________

Basic Examples on the Formulae “Area of a Triangle”

Case-I

Problems 37: What is the area of the triangle with two vertices A(1,2) and B(5,3) and height with respect to AB be 3 units in the coordinate plane ?

Solution: We already know,

If “h” be the height and “b” be the base of Triangle, then Area of the Triangle is = ½ × b × h

(See formulae chart)

image?w=366&h=269&rev=57&ac=1&parent=1Ug0lE5AOAhO4i0HE5fVqVUKTEbR0on8yfNNyWgAF Po — Graphical Representation

Using this formula we can say ,

h = 3 units and b = √

$(x2-x1)2+(y2-y1)2 $

i.e √

$(5-1)2+(3-2)2 $

Or, b = √

$(4)2+(1)2 $

Or, b = √

$(16+1 $

Or, b = √ 17 units

Therefore, the required area of the triangle is = ½ × b × h i.e

= ½ × (√ 17 ) × 3 units

= 3⁄2 × (√ 17 ) units (Ans.)

______________________________________________________________________________________

Case-II

Problems 38:What is the area of the triangle with vertices A(1,2), B(5,3) and C(3,5) in the coordinate plane ?

Solution: We already know,

If A(x₁,y₁) , B(x₂,y₂) and C(x₃,y₃) be the vertices of a Triangle,

Area of the Triangle is =|½

$x1 (y2- y3) + x2 (y3- y2) + x3 (y2- y1)$

(See formulae chart)

Using this formula we have ,

(x₁,y₁) ≌(1,2) i.e. x₁=1, y₁=2 ;

(x₂,y₂) ≌(5,3) i.e. x₂=5, y₂=3 and

(x₃,y₃) ≌(3,5) i.e. x₃=3, y₃=5

image?w=364&h=194&rev=207&ac=1&parent=1Ug0lE5AOAhO4i0HE5fVqVUKTEbR0on8yfNNyWgAF Po — Graphical Representation

Therefore, the area of the triangle is = |½

$x1 (y2- y3) + x2 (y3- y1) + x3 (y1-y2)$

| i.e

= |½

$1 (3-5) + 5 (5-3) + 3 (3-2)$

| sq.units

= |½

$1x (-2) + (5×2) + (3×1)$

| sq.units

= |½

$-2 + 10 + 3$

| sq.units

= |½ x 11| sq.units

= 11⁄2 sq.units

= 5.5 sq.units (Ans.)

More answered problems are given below for further practice using the procedure described in above problems :-

Problem 39: Find the area of the triangle whose vertices are (1,1), (-1,2) and (3,2).

Ans. 2 sq.units

Problem 40: Find the area of the triangle whose vertices are (3,0), (0,6) and (6,9).

Ans. 22.5 sq.units

Problem 41: Find the area of the triangle whose vertices are (-1,-2), (0,4) and (1,-3).

Ans. 6.5 sq.units

Problem 42: Find the area of the triangle whose vertices are (-5,0,), (0,5) and (0,-5). Ans. 25 sq.units

_______________________________________________________________________________________

For more post on Mathematics, please follow our Mathematics page.

13 Facts On Points In Coordinate Geometry In 2D

December 31, 2023June 19, 2021 by NASRINA PARVIN

This is a sequential post related to Co-ordinate Geometry, specially on Points. We already discussed few Topic earlier in the post “A Complete Guide to Coordinate Geometry”. In this post we will discuss the remaining topics.

Basic Formulae on Points in Co-ordinate Geometry in 2D:

All the basic formulae on points in Analytical Geometry are described here and for easy and quick learning at a glance about the formulae a ‘Formulae Table on Points’ with graphical explanation is presented below.

Two points distance formulae | Analytical Geometry:

Distance is a measurement to find how far objects, places etc. are from each other. It has a numerical value with units. In Co-ordinate Geometry or Analytical geometry in 2D, there is a formula which is derived from Pythagorean theorem ,to calculate the distance between two points. we can write it as ‘Distance’ d =√ [(x₂-x₁)²+(y₂-y₁)²] , where (x₁,y₁) and (x₂,y₂) are two points on the xy-plane. A brief graphical explanation is followed by ‘Formulae Table on Points topic no 1’ below.

A distance of a point from origin | Co-ordinate Geometry:

If we starts our journey with Origin in xy-plane and end up with any point of that plane, the distance between origin and the point can also be find by a formula, ‘Distance’ OP=√ (x²+ y²), which is also a reduced form of “Two points distance formula” with one point at (0,0). A brief graphical explanation is followed by ‘Formulae Table on Points topic no 2’ below.

Points section formulae |Coordinate Geometry :

If a point divides a line segment joining two given points at some ratio, we can use section formulae to find the coordinates of that point while the ratio at which the line segment is divided by, is given and vice versa. There is a possibility that the line segment can be divided either internally or externally by the point. When the point lies on the line segment between the two given points, Internal section formulae is used i.e.

$\\textbf{}\\textbf{x}\\textbf{=}\\frac{\\textbf{m}\\textbf{x}_{2}\\textbf{+}\\textbf{n}\\textbf{x}_{1}}{\\textbf{m}\\textbf{+}\\textbf{n}}$

and

$\\textbf{}\\textbf{y}\\textbf{=}\\frac{\\textbf{m}\\textbf{y}_{2}\\textbf{+}\\textbf{n}\\textbf{y}_{1}}{\\textbf{m}\\textbf{+}\\textbf{n}}$

And when the point lies on the external part of the line segment joining the two given points, external section formulae is used i.e.

$\\textbf{}\\textbf{y}\\textbf{=}\\frac{\\textbf{m}\\textbf{y}_{2}\\textbf{-}\\textbf{n}\\textbf{y}_{1}}{\\textbf{m}\\textbf{-}\\textbf{n}}$

Where (x , y) is supposed to be the required coordinates of the point. These are very necessary formulae to find the centroid, incenters ,circumcenter of a triangle as well as the center of mass of systems, equilibrium points etc. in physics. Must watch the short view of different types of section formulae with graphs given below in the ‘Formulae Table on Points topic no 3; case-I and case-II’.

Mid Point Formula| coordinate Geometry:

It is a easy formulae derived from Internal points section formulae described above. While we need to find the midpoint of a line segment i.e coordinate of the point which is equidistant from the two given points on the line segment i.e the ratio gets 1:1 form, then this formula is required. The formula is in the form of

If a point divides a line segment joining two given points at some ratio, we can use section formulae to find the coordinates of that point while the ratio at which the line segment is divided by, is given and vice versa. There is a possibility that the line segment can be divided either internally or externally by the point. When the point lies on the line segment between the two given points, Internal section formulae is used i.e.

$\\textbf{}\\textbf{x}\\textbf{=}\\frac{\\textbf{m}\\textbf{x}_{2}\\textbf{+}\\textbf{n}\\textbf{x}_{1}}{\\textbf{m}\\textbf{+}\\textbf{n}}$

and

$\\textbf{}\\textbf{y}\\textbf{=}\\frac{\\textbf{m}\\textbf{y}_{2}\\textbf{+}\\textbf{n}\\textbf{y}_{1}}{\\textbf{m}\\textbf{+}\\textbf{n}}$

And when the point lies on the external part of the line segment joining the two given points, external section formulae is used i.e.

$\\textbf{}\\textbf{x}\\textbf{=}\\frac{\\textbf{m}\\textbf{x}_{2}\\textbf{-}\\textbf{n}\\textbf{x}_{1}}{\\textbf{m}\\textbf{-}\\textbf{n}}$

and

$\\textbf{}\\textbf{y}\\textbf{=}\\frac{\\textbf{m}\\textbf{y}_{2}\\textbf{-}\\textbf{n}\\textbf{y}_{1}}{\\textbf{m}\\textbf{-}\\textbf{n}}$

Mid Point Formula| coordinate Geometry:

It is a easy formulae derived from Internal points section formulae described above. While we need to find the midpoint of a line segment i.e coordinate of the point which is equidistant from the two given points on the line segment i.e the ratio gets 1:1 form, then this formula is required. The formula is in the form of

$x=\\frac{x_{1}+x_{2}}{2}$

and

$x=\\frac{y_{1}+y_{2}}{2}$

Go through the “Formulae Table on Points topic no 3- case-III’ below to get the graphical idea on this.

Area of a triangle in Coordinate Geometry:

A triangle has three side and three vertices on the plane or in 2 dimensional field. Area of the triangle is the internal space surrounded by these three sides. The basic formula of area calculation of a triangle is (1/2 X Base X Height). In Analytical Geometry ,if the coordinates of all the three vertices are given, the area of the triangle can easily be calculated by the formula, Area of the Triangle =|½[x₁ (y₂– y₃ )+x₂ (y₃– y₂)+x₃ (y₂-y ₁)]| ,actually this can be derived from the basic formula of area of a triangle using two points distance formula in coordinate geometry. Both the cases are graphically described in the ‘Formulae Table on Points topic 4’ below.

Collinearity of points ( Three points) |Coordinate Geometry:

Collinear means ‘being on the same line’. In geometry, if three points lie on one single line in the plane, they never can form a triangle with area other than zero i.e. if the formula of area of triangle is substituted by the coordinates of the three collinear points, the result for area of the imaginary triangle formed by those points will end up with zero only. So the formula becomes like ½[x₁ (y₂– y₃ )+x₂ (y₃– y₂)+x₃ (y₂-y ₁)] =0 For more clear idea with graphical representation, go through the “Formulae Table on Points topic no 5” below.

Centroid of a triangle| Formula :

The three medians* of a triangle always intersect at a point, located in the interior of the triangle and divides the median in the ratio 2:1 from any vertex to the midpoint of the opposite side. This point is called the centroid of the triangle. The formula to find the coordinates of the centroid is

$x=\\frac{x_{1}+x_{2}+x_{3}}{3}$

and

$x=\\frac{y_{1}+y_{2}+y_{3}}{3}$

In the “Formulae Table on Points topic no 6” below, the above subject is described graphically for better understanding and for a quick view.

Incenter of a triangle|Formula:

It is the center of the triangle’s largest incircle which fits inside the triangle. It is also the point of intersection of the three bisectors of the interior angles of the triangle. The formula, used to find the incenter of a triangle is

$x=\\frac{ax_{1}+bx_{2}+cx_{3}}{a+b+c}$

and

$x=\\frac{ay_{1}+by_{2}+cy_{3}}{a+b+c}$

In the “Formulae Table on Points topic no 6” below, the above subject is described graphically for better understanding and for a quick view.

For easy graphical explanation the below “Formulae Table on Points topic no 7” is needed to see.

Shifting of Origin formula| Coordinate Geometry:

We have already learned in the previous post “A Complete Guide to Coordinate Geometry” that the origin lies on the point (0,0) which is the point of intersections of the axes in the plane. we can move the origin in all the quadrants of plane in respect with the origin , which will give new set of axes through it.

For a points in the above said plane , its coordinates will change along with the new origin and axes and that can be calculated by the formula, new coordinates of a point P(x₁,y₁) are x₁= x- a ; y₁ = y- b where the coordinates of the new origin is (a,b). To have clear understanding on this topic its preferable to see the graphical representation below in the “Formulae Table on Points topic no 8” .

`Formulae table on Points in Coordinate Geometry in 2D`:

﹡Circumcentre of a triangle :

It is the point of intersection of three perpendicular bisectors of the side of a triangle. It is also the center of a triangle’s circumcircle which only touches the vertices of the triangle.

﹡Medians:

Median is the line segment joining the vertex of triangle to the midpoint or the point, bisecting the opposite side of the vertex. Every triangle has three medians which always intersect each other at the centroid of the same triangle.

Solved Problems on Points in Coordinate Geometry in 2D.

For better learning about points in 2D, one basic example is solved here step by step and for practice on your own there are more problems with answers on each formula. There must be challenging problems with solution in the next articles just after getting a basic and clear idea on the topic of points in coordinate Geometry 2D.

Basic Examples on the Formulae “The distance between two points”

Problems 1: Calculate the distance between the two given points (1,2) and (6,-3).

Solution: We already know, the formula of the distance between two points (x₁,y₁) and (x₂,y₂) is d =√ [(x₂-x₁)²+(y₂-y₁)²] …(1)

(See the formulae table above) Here, we can assume that (x₁,y₁) ≌ (1,2) and (x₂,y₂) ≌ (6,-3) i.e x₁=1, y₁=2 and x₂=6, y₂ =-3 , If we put all these values in the equation (1),we get the required distance.

Therefore, the distance between the two points (1,2) and (6,-3) is

=√ [(6-1)²+(-3-2)²] units

= √ [(5)²+(-5)²] units

=√ [25+25] units

=√ [50] units

=√ [2×5²] units

= 5√2 units (Ans.)

Note: Distance is always followed by some units.

Problem 2: Find the distance between the two points (2,8) and (5,10).

Ans. √13 units

Problem 3: Find the distance between the two points (-3,-7) and (1,-10).

Ans. 5 units

Problem 4: Find the distance between the two points (2,0) and (-3,4).

Ans. √41 units

Problem 5: Find the distance between the two points (2,-4) and (0,0).

Ans. 2√5 units

Problem 6: Find the distance between the two points (10,100) and (-10,100,).

Ans. 20 units

Problem 7: Find the distance between the two points (√5,1) and (2√5,1).

Ans. √5 units

Problem 8: Find the distance between the two points (2√7,2) and (3√7,-1).

Ans. 4 units

Problem 9: Find the distance between the two points (2+√10, 0) and (2-√10, 0).

Ans. 2√10 units

Problem 10: Find the distance between the two points (2+3i, 0) and (2-3i, 10). { i=√-1 }

Ans. 8 units

Problem 11: Find the distance between the two points (2+i, -5) and (2-i, -7). { i=√-1 }

Ans. 0 units

Problem 12: Find the distance between the two points (7+4i,2i) and (7-4i, 2i). { i=√-1 }

Ans. 8i units

Problem 13: Find the distance between the two points (√3+i, 3) and (2√3+i, 5). { i=√-1 }

Ans. √7 units

Problem 14: Find the distance between the two points (5+√2, 3+i) and (2+√2, 7+2i). { i=√-1 }

Ans. 2√(6+2i) units

Basic Examples on the Formulae “The distance of a point from the origin”

Problems 15: Find the distance of a point (3,4) from the origin.

Solution:

We have the formula of the distance of a point from the origin, OP=√ (x²+ y²) (See the formulae table above) So here we can assume (x,y) ≌ (3,4) i.e x=3 and y=4

Therefore, putting these values of x and y in the above equation, we get the required distance

=√ (3²+ 4²) units

=√ (9+ 16) units

=√ (25) units

= 5 units

Note: Distance is always followed by some units.

Note: Distance of a point from the origin is actually the distance between the point and the point of origin i.e (0,0)

Problem 15:-

Problem 16: Find the distance of a point (1,8) from the origin.

Ans. √65 units

Problem 17: Find the distance of a point (0,7) from the origin.

Ans. 7 units

Problem 18: Find the distance of a point (-3,-4) from the origin.

Ans. 5 units

Problem 19: Find the distance of a point (10,0) from the origin.

Ans. 10 units

Problem 20: Find the distance of a point (0,0) from the origin.

Ans. 0 units

___________________________________________________________

Basic Examples on other Formulae of points described above and few challenging questions on this topic in coordinate Geometry, are followed by next posts.

Coordinate Geometry: 3 Things Most Beginner’s Don’t Know

December 31, 2023December 31, 2020 by NASRINA PARVIN

Coordinate Geometry

Today we are here to discuss Coordinate Geometry from the root of it. So, The whole article is about what Coordinate Geometry is, relevant problems and their solutions as much as possible.

(A) Introduction

Coordinate Geometry is the most interesting and important field of Mathematics. It is used in physics, engineering and also in aviation, rocketry, space science, spaceflight etc.

To know about Coordinate Geometry first we have to know what Geometry is.
In greek ‘Geo’ means Earth and ‘Metron’ means Measurement i.e. Earth Measurement. It is the most ancient part of mathematics, concerned with the properties of space and figures i.e positions, sizes, shapes, angles and dimensions of things.

What is Coordinate Geometry?

Coordinate geometry is the way of learning of geometry using the Co-ordinate system. It describes the relationship between geometry and algebra.
Many mathematicians also called Coordinate geometry as Analytical Geometry or Cartesian Geometry.

Why is it called Analytical Geometry?

Geometry and Algebra are two different branches in Mathematics. Geometrical shapes can be analyzed by using algebraic symbolism and methods and vice versa i.e. algebraic equations can be represented by Geometric graphs. That is why it is also called Analytical Geometry.

Why is it called Cartesian Geometry?

Coordinate Geometry was also named Cartesian Geometry after French mathematician Rene Descartes as he independently invented the cartesian coordinate in the 17th century and using this, put Algebra and Geometry together. For such a great work Rene Descartes is known as the Father of Coordinate Geometry.

(B) Coordinate system

A Coordinate system is the base of Analytical Geometry. It is used in both two dimensional and three-dimensional fields. There are four types of coordinate system in general.

(C) The whole subject of coordinate Geometry is divided into two chapters.

One is ‘Coordinate Geometry in Two Dimensions’.
The second one is ‘Coordinate Geometry in Three Dimensions’.

Coordinate Geometry in Two Dimensions (2D):

Here we are going to discuss both the Cartesian and Polar Coordinates in two dimensions one by one. We will also solve some problems to get a clear idea of the same, and later we will find the relation between them as well.

Cartesian Coordinate in 2D:

At first, we will have to learn the following terms through graphs.
i) Coordinate Axes
ii) Origin
iii)Coordinate Plane
iv) Coordinates
v) Quadrant

Read and Follow the Figures simultaneously.

Suppose the horizontal line XXand vertical line YY are two perpendicular lines intersecting each other at right angles at the point O , XXand YY are number lines, the intersection of XXand YY forms XY-plane and P is any point on this XY-plane.

Coordinate Axes in 2D

Here XX and YY are described as the Coordinate Axes. XX is indicated by X-Axis and YY is indicated by Y-Axis. Since XX and YY are number lines, the distances measured along OX and OY are taken as positive and also the distances measured along OX and OY are taken as negative. (See above graph.1)

What is Origin in 2D?

The point O is called the Origin. O is always supposed to be the starting point. To find the position of any point on the coordinate plane we always have to begin the journey from the origin. So the origin is called the Zero Point. (Please refer the above graph.1)

What do we understand by a Coordinate Plane?

The XY plane defined by two number lines XX and YY or the X-axis and Y- axis is called the Coordinate Plane or Cartesian Plane. This Plane extends infinitely in all direction. This is also known as two-dimensional plane. (See above graph.1)

*Assume the variables x>0 and y>0 in the above figure.

What is Coordinate in 2D?

Coordinate is a pair of numbers or letters by which the position of a point on the coordinate plane is located. Here P is any point on the coordinate plane XY. The coordinates of the point P is symbolized by P(x,y) where x is the distance of P from Y axis along X axis and y is the perpendicular distance of P from X axis respectively. Here x is called the abscissa or x-coordinate and y is called the ordinate or y-coordinate (See above Graph 2)

How to Plot a Point on the coordinate plane?

Always we will have to start from the origin and first walk towards right or left along X axis to cover the distance of x-coordinate or abscissa ,then turn the direction up or down perpendicularly to the X axis to cover the distance of ordinate using units and their signs accordingly. Then we reach the required point .

Here to represent the given point P(x,y) graphically or to plot it on the given XY plane, first start from the origin O and cover the distance x units along X axis (along OX) and then turn at 90 degree angle with X axis or parallelly to Y axis(here OY) and cover the distance y units . (See above graph 3)

How to find coordinates of a given point in 2D ?

Let XY be the given plane,O be the origin and P be the given point.
First draw a perpendicular from the point P on X axis at the point A. Suppose OA=x units and AP=y units, then the Coordinates of the point P becomes (OA , AP) i.e. (x,y).

Similarly if we draw another perpendicular from the point P on Y axis at the point B, then BP=x and OB=y.
Now since A is the point on the X axis ,the distance of A from Y axis along X axis is OA=x and perpendicular distance from X axis is zero,so the coordinates of A becomes (x,0).
Similarly, the coordinates of the point B on the Y axis as (0,y) and the coordinates of Origin O is (0,0).

Graph 5 * colour green denotes the beginning

What is Quadrant in 2D?

Coordinate Plane is divided into four equal sections by the coordinate axes. Each section is called Quadrant. Going around counterclockwise or anticlockwise from upper right, the sections are named in the order as Quadrant I, Quadrant II, Quadrant III and Quadrant iv.

Here we can see the X and Y axes divide the XY plane into four sections XOY, YOX, XOY and YOX accordingly. Therefore, the area XOY is the Quadrant I or first quadrant, YOX is the Quadrant II or second quadrant, XOY is the Quadrant III or third quadrant and YOX is the Quadrant IV or fourth quadrant.(please refer the graph 5)

Points in Different Quadrants of coordinate plane:

Since OX is +ve and OX is -ve side of X axis and OY is +ve and OY is -ve side of Y axis, signs of coordinates of points in different quadrants—-
Quadrant I: (+,+)
Quadrant II: (-,+)
Quadrant III: (-,-)
Quadrant IV: (+,-)

For example, if we go along OX from O and draw a perpendicular from any point P in the Quadrant I on the X axis (OX) at the point A so that OA=x and AP=y then coordinate of P is defined as (x,y) as described in the article (How to find coordinate of a given point?).

Again if we go along OX from O and draw a perpendicular from any point Q in the Quadrant II on the X axis (on OX) at the point C so that OC=x and CQ=y then the coordinates of Q is defined as (-x,y).
Similarly the coordinates of any point R in quadrant III is defined as (-x,-y) and the coordinates of any point in quadrant IV is defined as (x,-y). (see graph 6)

Conclusion

The brief information about Coordinate Geometry with basic concepts has been provided to get a clear idea to start the subject. We will subsequently discuss details about 2D and 3D in the upcoming posts. If you want further study go through:

Reference

1. https://en.wikipedia.org/wiki/Analytic_geometry
2. https://en.wikipedia.org/wiki/Geometry

For more topics on Mathematics, please follow this Link .

Locus in 2D Coordinate Geometry

Definition of Locus:

Examples on Locus:

Equation of the Locus:

Method of Obtaining the Equation of the Locus:

4+different types of solved problems on Locus:

More examples on Locus with answers for practice by your own:

Basic Examples on the Formulae “Centroid of a Triangle” in 2D Coordinate Geometry

More answered problems are given below for further practice using the procedure described in above problem 1 :-

Shifting of Origin / Translation of Axes- 2D Co-ordinate Geometry

The formula of ” Shifting of Origin” or “Translation of Axes” are described below with graphical representation.

Formula:

Few solved Problems on the formula of ‘Shifting of Origin’ :

Basic Examples on the Formulae “Collinearity of points (three points)” in 2D Coordinate Geometry

More answered problems are given below for further practice using the procedure described in the above problem 1 :-

Basic Examples on the Formulae “Incenter of a Triangle” in 2D Coordinate Geometry

More answered problems are given below for further practice using the procedure described in above problem 1 :-

Basic Examples on the Formulae “Point sections or Ratio”

Basic Formulae on Points in Co-ordinate Geometry in 2D:

Two points distance formulae | Analytical Geometry:

A distance of a point from origin | Co-ordinate Geometry:

Points section formulae |Coordinate Geometry :

Mid Point Formula| coordinate Geometry:

Mid Point Formula| coordinate Geometry:

Area of a triangle in Coordinate Geometry:

Collinearity of points ( Three points) |Coordinate Geometry:

Centroid of a triangle| Formula :

Incenter of a triangle|Formula:

Shifting of Origin formula| Coordinate Geometry:

Formulae table on Points in Coordinate Geometry in 2D:

﹡Circumcentre of a triangle :

﹡Medians:

Solved Problems on Points in Coordinate Geometry in 2D.

Basic Examples on the Formulae “The distance between two points”

Problems 1: Calculate the distance between the two given points (1,2) and (6,-3).

More answered problems (Basic) are given below for further practice using the procedure described in above Problem 1:-

Problem 2: Find the distance between the two points (2,8) and (5,10).

Problem 3: Find the distance between the two points (-3,-7) and (1,-10).

Problem 4: Find the distance between the two points (2,0) and (-3,4).

Problem 5: Find the distance between the two points (2,-4) and (0,0).

Problem 6: Find the distance between the two points (10,100) and (-10,100,).

Problem 7: Find the distance between the two points (√5,1) and (2√5,1).

Problem 8: Find the distance between the two points (2√7,2) and (3√7,-1).

Problem 9: Find the distance between the two points (2+√10, 0) and (2-√10, 0).

Problem 10: Find the distance between the two points (2+3i, 0) and (2-3i, 10). { i=√-1 }

Problem 11: Find the distance between the two points (2+i, -5) and (2-i, -7). { i=√-1 }

Problem 12: Find the distance between the two points (7+4i,2i) and (7-4i, 2i). { i=√-1 }

Problem 13: Find the distance between the two points (√3+i, 3) and (2√3+i, 5). { i=√-1 }

Problem 14: Find the distance between the two points (5+√2, 3+i) and (2+√2, 7+2i). { i=√-1 }

Basic Examples on the Formulae “The distance of a point from the origin”

Problems 15: Find the distance of a point (3,4) from the origin.

More answered problems are given below for further practice using the procedure described in above

Problem 15:-

Problem 16: Find the distance of a point (1,8) from the origin.

Problem 17: Find the distance of a point (0,7) from the origin.

Problem 18: Find the distance of a point (-3,-4) from the origin.

Problem 19: Find the distance of a point (10,0) from the origin.

Problem 20: Find the distance of a point (0,0) from the origin.

Basic Examples on other Formulae of points described above and few challenging questions on this topic in coordinate Geometry, are followed by next posts.

Coordinate Geometry

(A) Introduction

What is Coordinate Geometry?

Why is it called Analytical Geometry?

Why is it called Cartesian Geometry?

(B) Coordinate system

(C) The whole subject of coordinate Geometry is divided into two chapters.

Coordinate Geometry in Two Dimensions (2D):

Cartesian Coordinate in 2D:

Coordinate Axes in 2D

What is Origin in 2D?

What do we understand by a Coordinate Plane?

What is Coordinate in 2D?

How to Plot a Point on the coordinate plane?

What is Quadrant in 2D?

Points in Different Quadrants of coordinate plane:

Conclusion

Reference

`Formulae table on Points in Coordinate Geometry in 2D`: