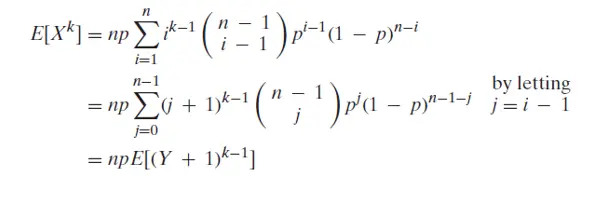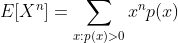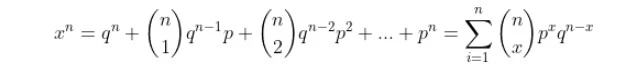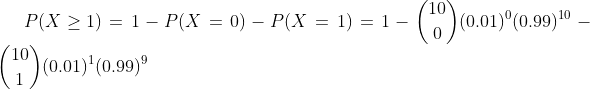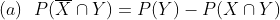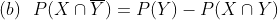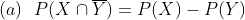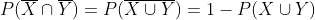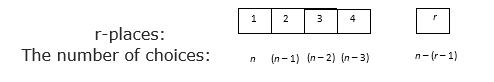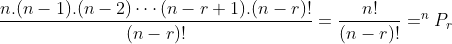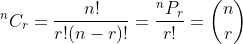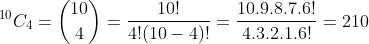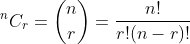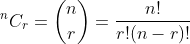Binomial & Poisson random variable and its properties

    The random variable which deals with the success and failure outcome of the random experiment for n repetitions were known to be Binomial random variable the definition of its probability mass function deals with the probability of success p and probability of failure q only, the definition with examples already we has seen, now with the understanding we see some of the properties of such discrete random variable,

Expectation and Variance of the binomial random variable

Expectation and Variance of binomial random variable with n repetition and p as probability of success are

E[X]= np

and Var(X) = np(1-p)

now consider for showing these two the expectation of random variable of power k by following  the definition of probability mass function for binomial random variable as,

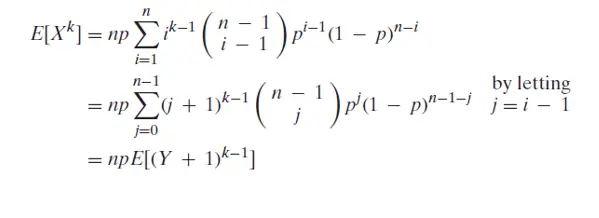
where Y is another binomial random variable with n-1 trials and p as the probability of success, If we take the value of k=1 then we will get

E[X]= np

and if we substitute k=2 we will get

E[X²] =npE[Y + 1]

=np[(n-1)p + 1]

so we will get easily

Var(X)=E[X²] – (E[X])²

=np[(n-1)p + 1] -(np)²

=np(1-p)

Example: For an unbiased coin do the experiment of tossing 100 times and for the number of tails that appearing in this case find the mean, variance and standard deviation of such experiment.

The tail for one toss has the probability of success p=1/2=0.5

so the mean of such experiment is

E[X]= np

since the experiment is binomial as only success or failure we will get for n number of repetitions

so as μ=np

μ=100x(0.5)=50

Similarly the variance and the standard deviation will be

Var(X)= np(1-p)

σ²= np(1-p)

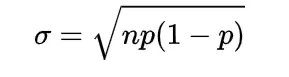
The value would be

σ² =(100)(0.5)(0.5)=25

Example:     Find the mean and standard deviation for the probability of 0.1 defectiveness in bolt manufacturing company from the lot of 400 bolt.

here n=400, p=0.1, mean= np =400×0.1=40

since

σ²= np(1-p)

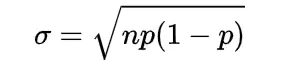
so standard deviation will be

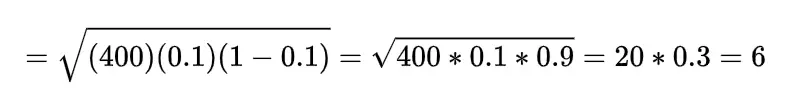
Example: Find the probability of exactly, less than and at least 2 successes if the mean and standard deviation for the binomial random variable is 4 and 2 respectively.

Since mean = np= 4

and variance = np(1-p) = 2,

so 4(1-p)=2

(1-p)=1/2

p=1-(1/2)

putting this value in mean we get

np = 4

n(1/2)=4

n=8

probability of exactly 2 successes will be

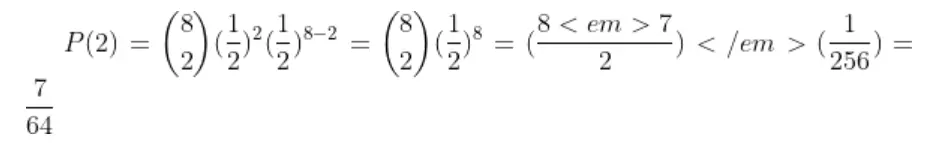
probability of less than 2 successes will be

p(X < 2)

=P(0) +P(1) = ⁸C₀ p⁰q⁸ + ⁸C₁ p¹q⁷

=(1/256)+8 x (1/2) x (1/2)⁷ = 9/256

Probability of at least 2 successes

p(X>2)= 1- p(X<2)

=1-P(0) – P(1)= 1-[P(0) + P(1)] =1- (9/256)=247/256

Poisson Random Variable

    The discrete random variable X that takes the values 0,1,2…….. is known to be Poisson Random variable provided for any λ>0 its probability mass function must be

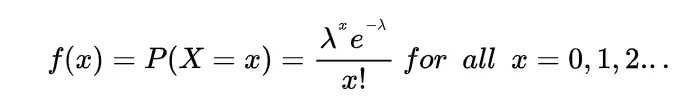
or

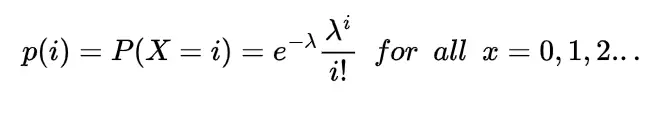
as

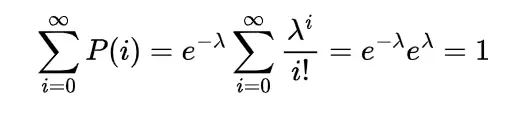
When n is very large and the probability of success p is very small in such case Poisson random variable with its probability mass function became the approximation of binomial random variate with respective p.m.f. because the expectation in this case which is np will be moderate and that would be λ= np .

Example: Find the probability that there is at least one typing error on each page of the book which has Poisson distribution with mean 1/2 for a single page.

Let the discrete random variable X denote the errors on the page. so the Poisson random variable has the probability mass function as

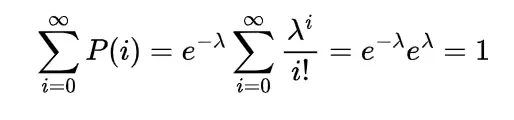
λ = 1/2

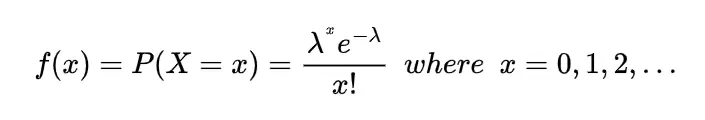
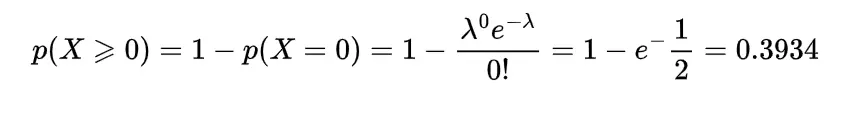
Example: Find the probability that the sample of 10 items produced by a machine with 0.1 chances of defective production has at the most one defective item.

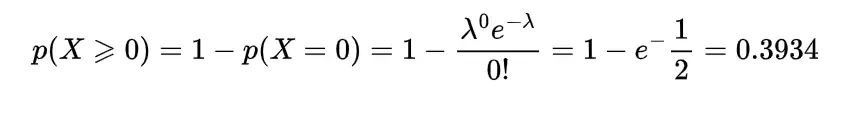
This we can solve both by binomial probability mass function as well as Poisson probability mass function, so we solve this by Poisson

Expectation and variance of the Poisson random variable

Expectation and Variance of Poisson random variable with n repetition and p as probability of success are

E[X]= np= λ

and          

Var(X) = np= λ

Before showing the result the we must keep in mind that the Poisson random variable is nothing but the approximation of Binomial random variable so np= λ now expectation by using the probability mass function will be

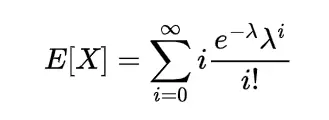
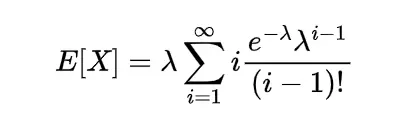
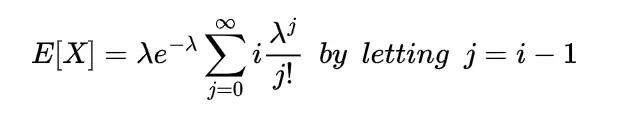
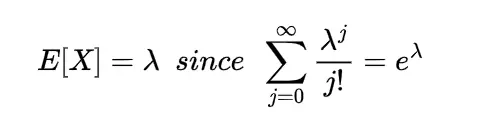
This means the mathematical expected value of Poisson random variable is equal to its parameter, similarly for calculating the variance and standard deviation of Poisson random variable we require expectation of square of X so,

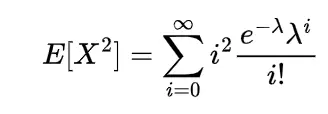
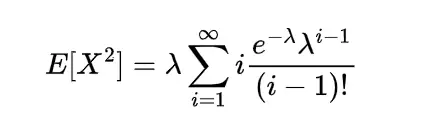
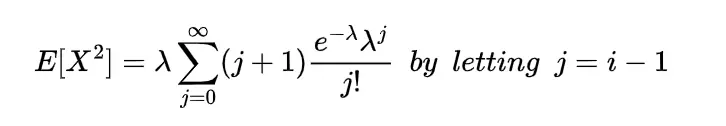
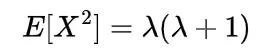
The above summation is obvious as two of the sums are expectation and sum of the probabilities.

Thus the value of variance we will get is

Var(X) = E[X²] – (E[X])²

=λ

so in the case of Poisson random variable the mean and variance have the same value i.e np as a parameter.

The Poisson random variable is the approximation good for the finding of diverse processes e.g. finding the occurrence of number of earthquakes within some specific time duration, finding the number of electron during a fixed time from the heated cathode, finding the possible number of deaths during specified time, or number of wars within specific year e.t.c.

Example : Calculate the probability that the total number of passengers in two days is less than 2. If the number of arrival of passengers with mean 5 follows Poisson random variable. mean=np=5

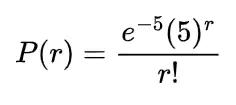
If we consider the number of passengers in two days less than 2 it would be

so the probability will be the combination of these two days as

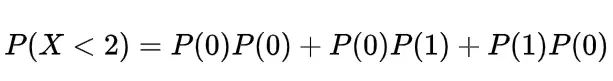
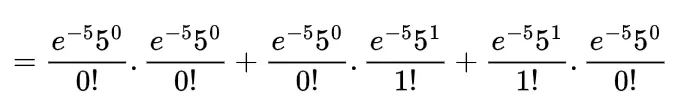
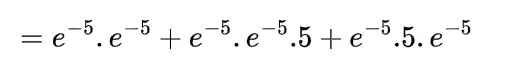
=e^-10[1+5+5]

=11e^-10

=114.5410^-5

=4.994*10^-4

Example: Calculate the probability of 4 or more faulty condensers from a pack of 100 condensers provided the manufacturing defect for the condensers is 1%.

Here p=1% =0.01 and n= 100 * 0.01 =1

so we can use the Poisson random variables probability mass function P.M.F

mean= np = 100*0.01=1

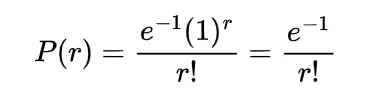
so the probability for 4 or more faulty condensers will be

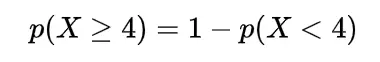
=1-[P(0)+P(1)+P(2)+P(3)]

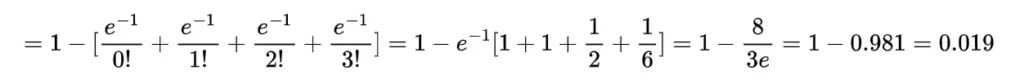
Example: If 0.002 chances are there for a product to be defective from the manufacturing, for a pack containing 10 of such products what would be the probability that such a packet has no defective, one defective, and two defective products from the consignment of 50000 packets of same product.

Here for a single pack probability of defect i.e p=0.002, n=10

then the mean np=0.002*10= 0.020

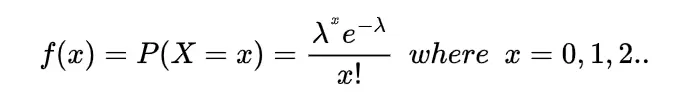
we will find for each case as

So from the table it is clear that the number of defective blades in packets zero, one and two will be 4900,980,10 respectively.

Conclusion:

   In this article we discussed some properties of one of Binomial random variable, Poisson random variable and Random Experiment.  Also one more discrete random variable i.e Poisson random variable, discussed with properties. The distribution for the probability mass function, expectation , variance and standard deviation example also taken for better understanding , In the next articles we try to cover some more discrete random variables if you want further reading then go through Mathematics Page.

Schaum’s Outlines of Probability and Statistics

https://en.wikipedia.org/wiki/Probability

Discrete Random Variable and Mathematical Expectation-II

As already we now familiar with the discrete random variable, it is the random variable which takes countable number of possible values in a sequence. The two important concept related to the discrete random variables are the probability of discrete random variable and distribution function we restrict the name to such probability and distribution function as,

Probability Mass function (p.m.f)

                The Probability Mass function is the probability of the discrete random variable, so for any discrete random variables  x₁, x₂, x₃, x₄,……, x_k  the corresponding probabilities P(x₁), P(x₂), P(x₃), P(x₄)……, P(x_k) are the corresponding probability mass functions.

Specifically, for X=a, P(a)=P(X=a) is its p.m.f

We here onwards use probability mass function for discrete random variables probability.  All the probability characteristics for the probability will obviously applicable to probability mass function like positivity and summation of all p.m.f will be one e.t.c.

Cumulative Distribution Function (c.d.f)/Distribution Function

  The distribution function defined as

F(x)=P(X<=x)

for discrete random variable with probability mass function is the cumulative distribution function (c.d.f.) of the random variable.

and mathematical expectation for such random variable we defined was

we now see some of the results of mathematical expectations

1. If x₁, x₂, x₃, x₄,….. are the discrete random variables with respective probabilities P(x₁), P(x₂), P(x₃), P(x₄) … the expectation for the real valued function g will be

Example: for the following probability mass functions find the E(X³)

Here the g(X)=X³

So,

E (X³) = (-1)³ <em>0.2 + (0)³</em> 0.5 + (1)³ * 0.3

E (X³) = 0.1

In the similar way for any nth order we can write

Which is known as nth moment.

2. If a and b are constants then

E[aX + b]=aE[X] + b

This we can understand easily as

=aE[X] + b

Variance in terms of Expectation.

                For the mean denoted by μ the variance of the discrete random variable X denoted by var(X) or σ in terms of expectation will be

Var(X) =E[(X- μ)²]

and this we can further simplify as

Var(X) =E[(X- μ)²]

= E [X²] – 2μ² + μ²

= E [X²] – μ²

this means we can write the variance as the difference of the expectation of random variable square and square of expectation of random variable.

i.e. Var (X)= E[X²] – (E[X])²

Example:  when a die is thrown calculate the variance.

Solution:  here we know when die thrown the probabilities for each face will be

p(1)=p(2)=p(3)=p(4)=p(5)=p(6)=1/6

hence for calculating variance we will find expectation of random variable and its square as

E[X]=1.(1/6)+2.(1/6)+3.(1/6)+4.(1/6)+5.(1/6)+6.(1/6)=(7/2)

E[X²] =1².(1/6)+2².(1/6)+3².(1/6)+4².(1/6)+5².(1/6)+6².(1/6) =(1/6)(91)

and we just obtained the variance as

Var (X) =E[X²] – (E[X])²

so

Var (X)=(91/6) -(7/2)² =35/12

One of the important identity for variance is

1. For the arbitrary constants a and b we have

Var(aX + b) =a² Var(X)

This we can show easily as

Var(aX + b) =E[(aX+ b -aμ-b)² ]

=E[a²(X – μ)²]

=a² E[(X-μ)²]

=a² Var(X)

Bernoulli Random variable

      A Swiss mathematician James Bernoulli define the Bernoulli random variable as a random variable having either success or failure as only two outcomes for the random experiment.

i.e When the outcome is success X=1

When the outcome is failure X=0

So the probability mass function for the Bernoulli random variable is

p(0) = P{X=0}=1-p

p(1) =P{X=1}=p

where p is the probability of success and 1-p will be the probability of failure.

Here we can take 1-p=q also where q is the probability of failure.

As this type of random variable is obviously discrete so this is one of discrete random variable.

Example: Tossing a coin.

Binomial Random Variable

If for a random experiment which is having only outcome as success or failure we take n trials so each time we will get either success or failure then the random variable X representing outcome for such n trial random experiment is known as Binomial random variable.

                In other words if p is the probability mass function for the success in  the single Bernoulli trial and q=1-p is the probability for the failure then the probability for happening of event ‘x or i’ times in n trials will be

or

Example: If we toss two coins six times and getting head is success and remaining occurrences are failures then its probability will be

in the similar way we can calculate for any such experiment.

The Binomial random variable is having the name Binomial because it represent the expansion of

If we put in place of n=1 then this would turn into the Bernoulli’s random variable.

Example: If five coins were tossed and the outcome is taken independently then what would be the probability for number of heads occurred.

Here if we take random variable X as the number of heads then it would turns to the binomial random variable with n=5 and probability of  success as ½

So by following the probability mass function for the binomial random variable we will get

Example:

In a certain company the probability of defective is 0.01 from the production. The company manufacture and sells the product in a pack of 10 and to its customers offer money back guarantee that at most 1 of the 10 product is defective, so what proportion of sold products pack the company must replace.

Here If X is the random variable representing the defective products then it is of the binomial type with n=10 and p=0.01 then the probability that the pack will return is

Example: (chuck-a-luck/ wheel of fortune) In a specific game of fortune in hotel a player bet on any of the numbers from 1 to 6, three dice then rolled and if the number appears bet by the player once, twice or thrice the player that much units means if appear once then 1 unit if on two dice then 2 units and if on three dice then 3 units, check with the help of probability the game is fair for the player or not.

If we assume there will be no unfair means with the dice and con techniques then by assuming the outcome of the dice independently the probability of success for each dice is 1/6 and failure will be

 1-1/6 so this turns to be the example of binomial random variable with n=3

so first we will calculate the winning probabilities by assigning x as players win

Now to calculate the game is fair for the player or not we will calculate the expectation of the random variable

E[X] = -125+75+30+3/216

= -17/216

This means the probability of losing the game for the player when he plays 216 times is 17.

Conclusion:

   In this article we discussed some of the basic properties of a discrete random variable, probability mass function and variance.  In addition we has seen some types of a discrete random variable, Before we start the continuous random variable we try to cover all the types and properties of discrete random variable, if you want further reading then go through:

Schaum’s Outlines of Probability and Statistics

https://en.wikipedia.org/wiki/Probability

For more Topics on Mathematics, please follow this link

Conditional probability

Conditional probability theory come out from the concept of taking huge risk. there are many issue now a days that stalk from the game of chance, such as throwing coins, throwing a dice, and playing cards. 

Conditional probability theory is applied in many different domains and the flexibility of Conditional probability provides tools for almost so many different needs. probability theory and samples related to the study of the probability of the happening of events.

Consider X and Y both are two events of a incidental experiment. Afterwards, the probability of the happenings of X under the circumstance that Y has already happened with P (Y) ≠ 0, is known as conditional probability and is denoted by P (X / Y).

Therefore, P (X / Y) = The probability of the happening of X, if provided that Y has already happened.

P(X ⋂ Y)/P( Y ) = n(X ⋂ Y)/n (Y )

Similarly, P (Y / X) = The probability of the occurrence of Y, as X has already happened.

P(X ⋂ Y)/P( X ) = n(X ⋂ Y)/n (Y )

In brief for some cases, P (X / Y) is used to specify the probability of the occurrence of X when Y occurs. Similarly, P (Y / X) is used to specify the probability of Y happening while X happens.

What is Multiplication theorem on Probability?

If X and Y both are self-supporting (independent) events of  a arbitrary experiment, then

P( X ⋂ Y) = P( X ). P( X/Y ), if P ( X ) ≠ 0

P( X ⋂ Y) = P( Y ). P( Y/X ), if P ( Y ) ≠ 0

What is Multiplication theorems for independent events? 

If X and Y both are self-supporting (independent) events connected to  a arbitrary experiment, then   P(X ∩ Y) =P(X).P(Y)

i.e., the probability of simultaneous happening of two independent events is equal to the multiplication of their probabilities. By using multiplication theorem, we have  P(X ∩ Y) =P(Y).P(Y/X)

 As X and Y are independent events, therefore P(Y/X)=P(Y)

Implies, P(X ∩ Y) =P(X).P(Y)

While events are mutually exclusive : 

If X and Y are mutually exclusive events, then ⇒ n(X ∩ Y)= 0 , P(X ∩ Y) = 0

P(X U Y)=P(X) +P(Y)

For any three events X, Y, Z which are mutually exclusive, 

P(X ∩ Y)= P(Y ∩ Z) =P(Z ∩ X) =P(X ∩ Y ∩ Z) =0

P (X ⋃ Y ⋃ Z) = P(X) + P(Y) + P(Z)

While events are independent : 

If X and Y are unconstrained (or independent) events, then

P(X ∩ Y) = P(X).P(Y)

P(X U Y) = P(X) + P(Y) – P(X). P(Y)

Let X and Y be two events connected with a arbitrary (or random) experiment, then

If Y⊂ X, then

(b) P(Y) ≤ P(X)

Similarly if X⊂ Y, then

(b) P(X) ≤ P(Y)

Probability of occurrence of neither X nor Y is 

Example: If from a pack of cards a single card is picked. What is the possible chance that it is either a spade or a king?

solution:

P (A) = P (a spade card) =13/52

P (B) = P (a king card) =4/52

P (either a spade or a king card) = P (A or B)

=P(A∪B)=P(A)+P(B)-P(A∩B)

=P(A)+P(B)-P(A)P(B)

=13/52+4/52-{(13/52)*(4/52)}

=4/13

Example: Someone is known to hit the target with 3 out of 4 chances, while another person is known to hit the target with 2 out of 3 chances. Find out if the probability that target are likely to be hit at all when both people are trying.

solution:

 probability of  target hit by first person = P (A) =3/4

probability of  target hit by second person = P (B) =2/3

The two events are not mutually exclusive, since both persons hit the same target   =P (A or B)

=P(A∪B)=P(A)+P(B)-P(A∩B)

=P(A)+P(B)-P(A)P(B)

=3/4+2/3-{(3/4)*(2/3)}

=11/12

Example: If  A  and B are two events such that P(A)=0.4 , P(A+B)=0.7 and P(AB)=0.2 then P(B) ?

solution: Since we have P(A+B)=P(A) +P(B) -P(AB)

=> 0.7=0.4+ P(B)-0.2

=> P(B) =0.5

Example: A card is selected at arbitrary from a pack of cards. What is the possibility of the card being a red color card or a queen.

Solution: Required probability  is

P(Red + Queen)-P(Red ⋂ Queen)

=P(Red) +P(Queen)-P(Red ⋂ Queen)

=26/52+4/52-2/52=28/52=7/13

Example: If the probability of X failing in the test is 0.3 and that the probability of Y is 0.2, then find the probability that X or Y failed in the test?

Solution: Here P(X)=0.3 , P(Y)=0.2

Now P(X ∪ Y)= P(X) +P(Y) -P(X ⋂ Y)

Since these are independent events, so

P(X ⋂ Y) =P(X) . P(Y)

Thus required probability is 0.3+0.2 -0.06=0.44

Example: The chances to fail in Physics are 20% and the possibility to fail in Mathematics are 10%. What are the possibilities to fail in at least one subject ?

Solution: Let P(A) =20/100=1/5, P(B) =10/100=1/10

Since events are independent and we have to find 

P(A ∪ B)=P(A) +P(B) -P(A). P(B)

=(1/5)+(1/10)-(1/5). (1/10)= (3/10)-(1/50)=14/50

So the chance of fail in one subject is (14/50)X 100=28%

Example: The probability of solving a question by three students are 1/2,1/4, and 1/6 respectively. What  will be the possible chance of answering the question?

Solution:

(i) This question can also be solved by one student

(ii) This question can be answered by two students concurrently.

(iii) This question can be answered by three students all together.

P(A)=1/2, P(B)=1/4, P(C)=1/6

P(A ∪ B ∪ C)= P(A) + P(B) +P(C)- [P(A).P(B)+P(B).P(C)+P(C).P(A)] + [P(A).P(B).P(C)]

=(1/2)+(1/4)+(1/6)-[(1/2).(1/4)+(1/4).(1/6)+(1/6).(1/2)] +[(1/2).(1/4).(1/6)] =33/48

Example: A random variable X has the probability distribution

For the events E ={X is prime number} and F={X<4},  find the probability of P(E ∪ F) .

Solution:

E ={ X is a prime number}

P(E) = P(2) +P(3)+ P(5) +P(7) =0.62

F ={X < 4}, P(F) =P(1)+P(2)+P(3)=0.50

and P(E ⋂ F) = P(2)+ P(3) =0.35

P(E ∪ F) =P(E)+P(F) – P(E ⋂ F)

      = 0.62+0.50 – 0.35 = 0.77

Example: Three coins are tossed. If one of them appears tail, then what would be the possible chance that all the three coins appear tail ?

Solution: Consider E is the event where all the three coins appears tail and F is the event where a coin appears tail. 

F= {HHT, HTH, THH, HTT, THT, TTH, TTT}

and E = {TTT}

Required probability = P(E/F)=P(E ⋂F )/P(E)=1/7

Total probability and Baye’s rule

The law of total probability :

For the sample space S and n mutually exclusive and exhaustive events E₁ E₂ ….E_n related with a random experiment. If X is a specific event which happens with the events E₁ or E₂ or …or E_n, then 

Baye’s rule : 

Consider S be a sample space and E₁, E₂, …..E_n be n incongruous (or mutually exclusive) events such that

and P(E_i) > 0 for i = 1,2,…,n

We can think of E_i’s as the factors leading to the outcome of the an experiment. The probabilities P(E_i), i = 1, 2, ….., n are called known as prior (or earlier) probabilities. If the assessment outcomes in an result of event X, where P(X) > 0. Then we have to perceive the possibility that the perceived the event X was due to cause E_i, that is, we look for the conditional probability P(E_i/X) . These probabilities are known as posterior probabilities, given by Baye’s rule as

Example: There are 3 Boxes which are known to contain 2 blue and 3 green marbles ; 4 blue and 1 green marbles and 3 blue and 7 green marbles respectively. A marble is drawn at random from one of the boxes and found to be a green ball. Then what is the probability that it was drawn from the Box containing the most green marbles.

Solution: Consider the following events :

A ->marble drawn is green;

E₁ -> Box 1 is chosen;

E₂ Box 2 is chosen

E₃ Box 3 is chosen.

P(E₁)=P(E₂)=P(E₃)=1/3 , p(A/E₁)=3/5

Then

P(A/E₂)=1/5, P(A/E₃)=7/10

Required probability =P(E₃/A)

P(E₃)P(A/E₃)/P(E₁)P(A/E₁)+P(E₂)P(A/E₂)+P(E₃)P(A/E₃)=7/15

Example: In an entrance test there are multiple choice questions. There are four probable correct answers to each question of which one is right. The possible chance that a pupil perceives the right answer to a particular question is 90%. If he gets the right answer to a particular question, then what is the probable chance that he was predicting.

Solution: We define the following events :

A₁ : He knows the answer.

A₂ : He might not know the answer.

E: He is aware of the right answer.

P(A₁) =9/10, P(A₂) =1-9/10=1/10, P(E/A₁)=1,

P(E/A₂) = 1/4

So the expected probability

Example: Bucket A contains 4 Yellow and 3 Black Marbles and Bucket B contains 4 Black and 3 Yellow Marbles. One Bucket is taken at random and a Marble is drawn and noted it is Yellow. What is the probability that it comes Bucket B.

Solution: It is based on Baye’s theorem. 

Probability of picked Bucket A , P(A)=1/2

Probability of picked Bucket B , P(B)=1/2

Probability of Yellow Marble picked from Bucket A  =P(A). P(G/A)=(1/2)x (4/7)=2/7 

Probability of Yellow Marble picked from Bucket B = P(B).P(G/B)=(1/2)x(3/7)=3/14

Total probability of Yellow Marbles= (2/7)+(3/14)=1/2

Probability of fact that Yellow Marbles is drawn from Bucket B  

P(G/B)={P(B).P(G/B)}/{P(A).P(G/A)+P(B).P(G/B)}={(1/2)x(3/7)}/{[(1/2)x(4/7)]+[(1/2)+(3/7)]} =3/7

Conclusion:

 In this article we mainly discuss on the Conditional Probability and Bayes theorem with the examples of these the direct and dependent consequence of the trial we discuss so far now in the consecutive articles we relate probability to random variable and some familiar terms related to probability theory we will discuss, if you want further reading then go through:

Schaum’s Outlines of Probability and Statistics and Wikipedia page.

For further study, please refer our mathematics page.

  After discussing the definitions and basic concepts we will enlist all the results and relations of permutation and combination, depending on all those we will get more familiar with the concept of permutation and combination by solving miscellaneous examples.

Points to remember (Permutation)

1. The number of ways of ordering = ⁿP_r={n(n-1)(n-2)…..(n-r+1)((n-r)!)}/(n-r)!= n!/{(n-r)!}
2. The number of arranging of n different objects taken all together at a time is = ⁿP_n =n!
3. ⁿP₀ =n!/n!=1
4. P=n. ^n-1P_r-1
5. 0!=1
6. 1/(-r)!=0 , (-r)!=∞ (r∈ N)
7. The number of ways of filling r places where every place can be filled by any one of n objects, The count of permutations = The number of ways of stuffing r places =(n)^r   

Example: How many numbers between 999 and 10000 can be generated with the help of numbers 0, 2, 3,6,7,8 where the digits must not be duplicated?

Solution: The numbers in between 999 and 10000 all are of four digit numbers.

                   The four-digit numbers constructed by digits 0, 2, 3,6,7,8 are

  But here those numbers are also involved which begin from 0. So we can take the numbers which are formed with three digits.

Taking initial digit 0, the number of ways to arrange pending 3 places from five digits 2, 3,6,7,8 are ⁵P₃ =5!/(5-3)!=2!*3*4*5/2!= 60

So the required numbers = 360-60 = 300.

Example: How many books can be set out in a row so that the two books mentioned are not together?

Solution: Total number of orders of n different books =n!.                                                                                                                

           If two mentioned books always together then number of ways =(n-1)!x2

Example: How many ways are there divided by 10 balls between two boys, one getting two and the other eight.

Solution: A gets 2, B  gets 8;  10!/2!8!=45

                  A gets 8, B gets 2; 10!/(8!2!)=45

that means 45+45=90 ways the ball will be divided.

Example: Search the number of arranging of the alphabets of the word “CALCUTTA”.

Solution: Required number of ways =8!/(2!2!2!)=5040

Example: Twenty people have been invited to the party. How many different ways in which they and the host can sit at a round table, if the two people have to sit on either side of the keeper.

Solution: There will be total 20 + 1 = 21 persons in all.

The two specified persons and the host be considered as one unit so that these remain 21 –  3 + 1 = 19 persons to be arranged in 18 ! ways.

 But the two particular person on either side of the host can themselves be arranged in 2! ways.

  Hence there are 2 ! *18 ! ways.

Example : In how many ways a garland can be made from exactly 10 flowers.

Solution:  n flowers’ garland can be made in (n-1)! ways.

Using 10 flowers garland can be prepared in 9!/2 different ways.

Example: Find the specific four-digit number which should be formed by 0, 1, 2, 3, 4, 5, 6, 7 so that each and every number has the number 1.

Solution: After securing 1 at first position out of 4 places 3 places can be filled by⁷P₃ =7!/(7-3)!=5*6*7=210 ways.

But some numbers whose fourth digit is zero, so such type of ways =⁶P₂=6!/(6-2)!=20.

                   Total ways = ⁷P₃ – ⁶P₂ =210-20=180

Keep these Points in mind for Combination

In continuation we will solve some examples  

Example: If ¹⁵C_r=¹⁵C_r+5 , then what is the value of r?

Solution: Here we will use the above

 ⁿC_r=ⁿC_n-r on the left side of the equation

¹⁵C_r=¹⁵C_r+5 => ¹⁵C_15-r =¹⁵C_r+5

=> 15-r=r+5 => 2r=10 => r=10/2=5

so the value of r is 5 implies the problem of 15 CHOOSE 5.

Example: If ²ⁿC₃ : ⁿC₂ =44:3   find the value of r, So that the value of ⁿC_r  will be 15.

 Solution: Here the given term is the ratio of 2n choose 3 and n choose 2 as

by the definition of combination

(2n)!/{(2n-3)!x3!} X {2!x(n-2)!}/n!=44/3

=> (2n)(2n-1)(2n-2)/{3n(n-1)}=44/3

=> 4(2n-1)=44 =>2n=12 => n=6

                   Now ⁶C_r=15 => ⁶C_r=⁶C₂   or ⁶C₄ => r=2, 4

so the problem is turned out to be 6 choose 2 or 6 choose 4

Example:  If  ⁿC_r-1= 36 ⁿC_r=84 and ⁿC_r+1=126 , then what would be the value of r ?

 Solution : Here ⁿC_r-1 / ⁿC_r =36/84 and ⁿC_r /ⁿC_r+1 =84/126 .

(n)!/{(n-r+1)!x(r-1)!} X {(r)!x(n-r)!}/(n)!=36/84

r/(n-r+1)=3/7 => 7r=3n-3r+3

=> 3n-10r=-3, and similarly from second ration we get

4n-10r=6

On solving, we get n=9, r=3

so the problem turned out to be 9 choose 3 , 9 choose 2 and 9 choose 4.

Example: Everyone in the room shakes hands with everyone. The total count of handshaking are 66. Find the number of person in the room.

ⁿC₂ =66 => n!/{2!(n-2)!}=66 => n(n-1)=132 => n=12

Solution: so the value of n is 12 implies the total number of people in the room is 12 and the problem is 12 choose 2.

Example: In a football tournament, 153 games were played. All teams played one game. find the number of groups involved in tournament.

Solution:

here ⁿC₂ =153 => n!/{2!(n-2)} = 153 => n(n-1)/2=153 => n=18

so the total number of teams participated in the tournament were 18 and the combination is 18 choose 2 .

Example During the Deepawali ceremony each club member sends greeting cards to others. If there are 20 members in the club, what would be the total number of ways greeting cards exchanged by the members.

Solution: Since two members can exchange cards each other in two ways so there is 20 choose 2 two times

2 x ²⁰C₂ =2 x (20!)/{2!(20-2)!}=2*190=380, there would be 380 ways to exchange greeting cards.

Example: Six plus ‘+’ and four minus ‘-’ symbols should be arranged in such a straight line so that no two ‘-’ symbols meet, find  the total number of ways .

 Solution: The ordering can be make as -+-+-+-+-+-+- the (-) signs can be put in 7 vacant (pointed) place.

Hence required number of ways = ⁷C₄ =35 .

Example: If ⁿC₂₁ =ⁿC₆ , then  find ⁿC₁₅ =?

Solution: Given ⁿC₂₁ =ⁿC₆

21+6=n => n=27

Hence ²⁷C₁₅ =27!/{15!(27-15)!} =17383860

which is the 27 choose 15.

Conclusion

Some examples are taken depending on the relations and results, as number of examples we can take on each of the result but the important thing here I want to show was how we can use any result depending on the situation if you require further reading you can go through the content or if any personal help then you can free to contact us some of the related content you can find from:

For more topics on Mathematics, please check this link.

SCHAUM’S OUTLINE OF Theory and Problems of DISCRETE MATHEMATICS

https://en.wikipedia.org/wiki/Permutation

https://en.wikipedia.org/wiki/Combination

Discrete Random Variable and Mathematical Expectation

Usually we are not interested in all the possible outcome of any random or non-random experiment instead we are interested in some probability or numerical value for the favorable events, for example suppose we are throwing two dice for the sum as 8 then we are not interested in the outcome as first dice having 2 second dice as 6 or (3,5), (5,3), (4,4), (6,2),etc. likewise for the random of experiment of reservoir in daily life we are not interested in the daily increase or decrease of water level but only interested in the rainy season water level after completion.

So such numerical quantities in which we are interested are considered as random variable of the respective random experiment.  For this purpose we assign the possible real values to the outcomes of the random experiment numerically. For illustration of assigning numerical value to the outcome consider the experiment of tossing a coin, we assign numerical value 0 and 1 for head and trail respectively in sample space of the random experiment. 

Discrete Random Variable

Discrete random variable can be define as the random variable which are finite or countably infinite in number and those who are not finite or countably infinite are Non-discrete random variables.  For every element of sample space we are assigning a real number, this can be interpreted in terms of real valued function denoted by X i.e. X:S→R. We call this function as a random variable or stochastic function, which has some physical, geometric or any other importance.

Example: Consider an experiment of throwing two dice then suppose random variable or stochastic function represent sum of the points appeared on the dice then the possible values for the sample space

S={(1,1), (1, 2), (1,3), (1,4), (1,5) , (1,6) ,

          (2,1), (2,2), (2,3), (2,4), (2,5), (2,6),

          (3,1), (3,2), (3,3), (3,4), (3,5), (3,6),

        (4,1), (4,2), (4,3), (4,4), (4,5), (4,6),

        (5,1), (5,2), (5,3), (5,4), (5,5), (5,6),

        (6,1), (6,2), (6,3), (6,4), (6,5), (6,6)}

will be X=2, for (1,1)

X=3 for (1,2), (2,1) etc from the following we can understand easily

In the above table the diagonal elements from right to left will give the sum expressed by the random variable or stochastic function.

The probability for the respective random variable can be expressed as follows

Discrete Probability Distribution

Discrete probability distribution is the probabilities of the random variables which are discrete in nature, in particular if x₁, x₂, x₃, x₄, ………., x_k are the values of discrete random variable X then P(x₁), P(x₂), P(x₃), P(x₄), ……… .P(x_k) are the corresponding probabilities.

Probability function/probability distribution we can denote as 

P(X=x)=f(x)

and following the definition of the probability this function satisfies following conditions.

1. f(x)≥0
2. Σ f(x)=1, where this summation is total summation for x.

Example: If a coin tossed two times, then if we express the number of trails come up as random variable X, then it would be 

If we take the fair coin then the above will be the outcome for tossing twice and the probability for such random variable will be

P (X=0) = P (H,H) =1/4

P (X=1) = P (TH or HT) = P (TH ∪ HT) = P ( TH) + P ( HT)=1/4+1/4=1/2

and P ( X=2) = P (TT) =1/4

This probability distribution we can tabulate as follows

Cumulative Distribution Function (c.d.f)/Distribution Function

We will define Distribution function or Cumulative Distribution Function (c.d.f) for the discrete random variable X denoted by F(x), for-∞≤x≤∞ as

F(x)=P(X≤x)

Provided it follows

1. For any x,y , x≤y, F(x) ≤ F(y) i.e. cumulative distribution function F(x) is non-decreasing.
2. F(x) =0 and F(x)=1
3. F(x+h)=F(x),   ∀ x i.e. . cumulative distribution function F(x) is right continuous.

Since for the discrete random variable probability for X=x is P(X=x), for x₁<X<x₂ will be P(x₁<X<x₂) and for X≤x is P(X≤x).

We can write the Distribution function for discrete distribution function as follows

we can obtain the probability function from the distribution function as

P (X=x) = f(x) =F(x)-F(u)

Example: The probability for the discrete random variable is given as follows

Find F2, F5, F(7)?

Solution:

Mathematical Expectation 

   Mathematical expectation is very important concept for the probability theory as well as statistics point of view it is also known as the expectation or expected value, it can be defined as the summation of random variables and its probabilities in multiplication i.e if x₁, x₂, x₃, x₄, ……….x_n are the values of discrete random variable X then P(x₁),P(x₂),P(x₃),P(x₄),……….P(xn) are the corresponding probabilities then mathematical expectation of random variable X denoted by E(x)  as

Example: From a pack of 72 cards numbered from 1 to 72 at a time 8 cards are drawn, find the expected value of the sum of numbers on tickets drawn.

Solution:.  consider the random variables x₁, x₂, x₃, x₄,……….x_n representing the cards numbered 1, 2, 3, 4, ………, 72

so probability of any x out of 72 card is 

P(x_i)=1/n=1/72

since then expectation will be

E(x)=x₁.(1/n)+x₂.(1/n)+x₃.(1/n)+……………+x_n.(1/n)

E(x)=1.(1/n)+2.(1/n)+3.(1/n)+……………+72.(1/n)

={1+2+3+……………..+72}*(1/72)=72*(72+1)/2*(1/72)=73/2

Now the expected value for 8 such cards will be 

E(x)=x₁.(1/n)+x₂.(1/n)+x₃.(1/n)+……………+x₈.(1/n)

E(x)=1.(1/n)+2.(1/n)+3.(1/n)+……………+8.(1/n)

={1+2+3+……………..+8}*(1/72)

=8*(8+1)/2*(1/72)=12

Variance, Standard deviation and Mean deviation by Mathematical Expectation

The important concepts of the statistics standard deviation and variance we can express in terms of mathematical expectation, so if the random variables x₁, x₂, x₃, x₄, ……….x_n with the corresponding probabilities  P(x₁), P(x₂), P(x₃), P(x₄), ……….P(x_n)  then variance will be

Example: In a game if a fair dice is used and player will win if any odd value come on dice  and prize money will be given Rs 20 if 1 come, Rs 40  for 3, and Rs 60 for  5 and if any other face of the dice came Rs 10 loss for the player. find the expected money that can be won with variance and standard deviation.

Solution:

For the fair dice we know the distribution of the probabilities,

Let X be the random variable for the dice convert as per the game requirement money won or loss when face came as follows,

so the expected amount won by any player will be

  E(x)=(20).(1/6)+(-10).(1/6)+(40).(1/6)+(-10).(1/6)+(60).(1/6)+(-10).(1/6)=15

so the expected amount won by any player would be μ=15

The result of the mathematical expectation as well as variance can be generalized for more than two variables as per requirement.

Conclusion:

   In this article we mainly discussed the discrete random variable, probability distribution and distribution function known as cdf cumulative distribution function, Also the concept of Mathematical Expectation for discrete random variable and what would be the mean deviation, variance and standard deviation for such discrete random  variable is explained with the help of suitable examples in next article we will discuss the same for continuous random variable, if you want further reading then go through:

For more topic on Mathematics, please follow this link.

Schaum’s Outlines of Probability and Statistics

https://en.wikipedia.org/wiki/Probability

Properties of Permutation and combination

  When discussing permutation and combination as we are dealing with selection and arrangement with or without order considerations, depending on the situation there are different types and properties for the permutation and combination, these differences among permutations and combinations we will explain here with justified examples.

permutations without repetition

  This is the normal permutation which arranges n objects taken r at a time i.e nPr

ⁿ P_r=n!/(n-r)!

number of orderings of n different objects taken all at a time ⁿ P_n =n!

In addition, we have

ⁿP₀ = n!/n!=1

ⁿP_r = n.^n-1P_r-1

0!=1

1/(-r)!= 0 or (-r)!=∞

permutations with repetition

 Number of permutations (arrangements) for different items, taken r at a time, where each item can happen once, twice, three times, …….. r-times as many in any arrangement = Number of ways to fill r areas where each item can be filled with any of the n items.

The number of permutations = The number of ways of filling r places = (n)^r

The number of orders that can be organized using n objects out of which p are alike (and of one kind) q are alike (and of another kind), r are similar (and of another kind) and the rest are distinct is ⁿP_r =n!/(p!q!r!)

Example:

In how many ways can 5 apples be allocated among four boys when every boy can take one or more apples.      

Solution: This is the example of permutation with repetition as we know that for such cases we have

The number of permutations = The number of ways of filling r places =n^r

Required number of ways are 4⁵ =10, Since each apple can be distributed in 4 ways.

Example: Find the number of words can be organized with the letters of the word MATHEMATICS by regrouping them.

Solution: Here we can observe that there are 2 M’s, 2 A’s and 2T’s this is the example of permutation with repetition

=n!/(p!q!r!)

 Required number of ways are =11!/(2!2!2!)=4989600

Example: How many ways in which the number of tails equal to the number of heads if six identical coins are arranged in a row.

Solution: Here we can observe that

No. of heads=3

No. of tails =3

And since coins are identical this is the example of permutation with repetition =n!/(p!q!r!)

Required number of ways =6!/(3!3!)= 720/(6X6)=20

Circular permutation:

In circular permutation, most importantly the ordering of the object is respect to the others.

So, in circular permutation, we adjust the position of one object and arrange the other objects in all directions.

Circular permutation is split into two ways:

(i) Circular permutation where clockwise and anti-clockwise settings suggest different permutation, e.g. Arrangements for seating people around the table.

(ii) Circular permutation where clockwise and anti-clockwise settings display same permutation, e.g. arranging certain beads to create a necklace.

Clockwise and anti-clockwise arrangement

If the anti-clockwise and clockwise order and movement are not different eg, bead arrangement in necklace, flower arrangement in garland etc, then the number of circular permutations of n distinct items is (n-1)!/2

1. The number of circular permutation for n different items, taken r at a time, when the orders for the clockwise and the anti-clockwise  are considered to be different by ⁿP_r /r
2. The number of circular permutation for n different items, taken r at a time, when clockwise and anti-clockwise orders are not different from ⁿP_r /2r
3. The number of circular permutations of n different objects are (n-1)!
4. The number of ways in which n different boys can be seated round a circular table is (n-1)!
5. The number of ways in which n different gems can be set up to form a necklet, is (n-1)!/2

Example:

How many ways can five keys be placed in the ring

Solution:

Since clockwise and anticlockwise are same in case of ring.

If the anti-clockwise and clockwise sequence and movement are not different then the number of circular permutations of n distinct items is

=(n-1)!/2

Required number of ways = (5-1)!/2= 4!/2=12     

Example:

What would be the number of arrangements, If eleven members of a committee sit at a round table so that the President and Secretary always sit together.

Solution:

By fundamental property of circular permutation

The count of circular permutations of n different things are (n-1)!

Since two positions are fix so we have

Required number of ways (11-2)!*2=9!*2=725760

Example: What would be number of ways 6 men and 5 women can eat at a round table if no two women can sit together

Solution: By fundamental property of circular permutation.

The count of circular permutations of n different things are (n-1)!

Number of ways in which 6 men can be arranged at a round table = (6 – 1)!  =5!

Now women can be arranged in 6! ways and Total Number of ways = 6! × 5!

Combinations without repetition

This is the usual Combination which is “The number of combinations (selections or groups) that can be formed from n different objects taken r at at a time is ⁿC_r =n!/(n-r)!r!

Also    ⁿC_r =ⁿC_r-r

              ⁿ P_r /r! =n!/(n-r)! =ⁿC_r

Example: Find the number of options to fill 12 vacancies if there are 25 candidates and five of them are from the scheduled category, provided that 3 vacancies are reserved for the S.C candidates mean while the remaining are open to everyone.

Solution: Since 3 vacant positions are filled from 5 applicants in ⁵ C₃  ways (i.e 5 CHOOSE 3) and now remaining candidates are 22 and remaining seats are 9 so it would be ²²C₉ (22 CHOOSE 9) The selection can be made in ⁵ C₃  X ²²C₉ ={5!/3!(5-3)! }X{22!/9!(22-9)!}

⁵ C₃  X ²²C₉ = {(3!X4X5)/(3!X2!)}X {22!/(9!X13!)}=4974200

So the selection can be made in 4974200 ways. 

Example: There are 10 candidates and three vacancies in the election. in how many ways a voter can cast his or her vote?

Solution: Since there are only 3 vacancies for 10 candidates so this is the problem of 10 CHOOSE 1, 10 CHOOSE 2, and 10 CHOOSE 3 Examples,

A voter can vote in ¹⁰C₁+¹⁰C₂+¹⁰C₃ = {10!/1!(10-1)!}+{10!/2!(10-2)!}+{10!/3!(10-3)!} =10+45+120= 175 ways.

 So in 175 ways voter can vote.

Example:There are 9 chairs in a room for 4 people, one of which is a single-seat guest with one specific chair. How many ways can they sit?

Solution: Since 3 chairs can be select in ⁸C₃ and then 3 persons can be arranged in 3! ways.

3 persons are to be seated on 8 chairs ⁸C₃ (i.e 8 CHOOSE 3) arrangement

=⁸C₃ X3! = {8! /3!(8-3)!} X3!

=56X6=336

In 336 ways they can sit.

Example: For five men and 4 women, a group of 6 will be formed. In how many ways this can be done so that the group has more men.

Solution: Here the problem include different combinations like 5 CHOOSE 5, 5 CHOOSE 4, 5 CHOOSE 3 for men and for women it include 4 CHOOSE 1, 4 CHOOSE 2 and 4 CHOOSE 3 as given in the followings

1 woman and 5 men =⁴C₁ X ⁵C₅ ={4!/1!(4-1)!} X{5!/5!(5-5)!}=4

           2 women and 4 men =⁴C₂ X ⁵C₄ = {4!/2!(4-2)!} X{5!/4!(5-4)!}=30

           3 women and 3 men =⁴C₃ X ⁵C₃ = {4!/3!(4-3)!} X {5!/3!(5-3)!} =40

    Hence total ways = 4+30+40=74.

Example: The number of ways 12 boys can travel in three cars so that 4 boys in each car, assuming that three particular boys will not go in the same car.

Solution: First omit three particular boys, remaining 9 boys may be 3 in each car. This can be done in 9 CHOOSE 3 i.e ⁹C₃ ways,

The three particular boys may be placed in three ways one in each car. Therefore total number of ways are =3X⁹C₃.

={9!/3!(9-3)!}X3= 252

so in 252 ways they can be placed.

Example: How many ways did 2 green and 2 black balls come out of a bag containing 7 green and 8 black balls?

Solution: Here bag contains 7 green from that we have to choose 2 so it is 7 CHOOSE 2 problem and 8 black balls from that we have to choose 2 so it is 8 CHOOSE 2 problem.

Hence the Required number = ⁷C₂ X ⁸C₂ = {7!/2!(7-2)!}X{8!/2!(8-2)!}=21X28=588

so in 588 ways we can select 2 green and 2 black from that bag.

Example: Twelve different characters of English words are provided. From these letters, 2 alphabetical names are formed. How many words can be created when at least one letter is repeated.

Solution: here we have to choose 2 letter words from 12 letters so it is 12 CHOOSE 2 problem.

No. of words of 2 letters in which letters have been recurrent any times = 12²

        But no. of words on having two different letters out of 12 =¹²C₂ = {12!/2!(12-2)!} =66

        Required number of words = 12²-66=144-66=78.

Example: There are 12 points on the plane where six are collinear, then how many lines can be drawn by joining these points.

Solution: For 12 points in a plane to make line we require 2 points same for six collinear points, so this is 12 CHOOSE 2 and 6 CHOOSE 2 problem.

The number of lines is = ¹²C₂ – ⁶C₂ +1={12!/2!(12-2)!}-{6!/2!(6-2)!}+1 =66-15+1=52

So in 52 number of ways it lines can be drawn.

Example: Find the numeral of ways in which a 6-member cabinet can be set up from 8 gentlemen and 4 ladies so that the cabinet consists of at least 3 ladies.

Solution: For forming the committee, we can choose from 3 each men and women and 2men 4 women so the problem includes 8 CHOOSE 3, 4 CHOOSE 3, 8 CHOOSE 2 and 4 CHOOSE 4.

Two types of cabinet can be formed

        (i) Having 3 men and 3 ladies

        (ii) Having 2 men and 4 ladies

        Possible no. of ways =  (⁸C₃ X ⁴C₃) + (⁸C₂ X⁴C₄)= {8!/3!(8-3)!}X{4!/3!(4-3)!} +{8!/2!(8-2)!}X{4!/4!(4-4)!} = 56X4+ 28X1 =252      

So In 252 ways we can form such cabinet.

       These are some examples where we can compare the situation of ⁿP_r vs ⁿC_r in the case of permutation, the way things are organized is important. However in Combination the order means nothing.

Conclusion

A brief description of Permutation and combination when repeated and non-repeated with the basic formula and important results is provided in the form of real examples, in this series of articles we will discuss in detail the various outcomes and formulas with relevant examples, if you want to continue reading:

SCHAUM’S OUTLINE OF Theory and Problems of DISCRETE MATHEMATICS

https://en.wikipedia.org/wiki/Permutation

https://en.wikipedia.org/wiki/Combination

For more Article on Mathematics, please follow this Link

Illustration of the concept Permutations and Combinations by the examples

In this article, we have discussed some examples which will make the foundation strong of the students on Permutations and Combinations to get the insight clearance of the concept, it is well aware  that the Permutations and combinations both are the process to calculate the possibilities, the difference between them is whether order matters or not, so here by going through the number of examples we will get clear the confusion where to use which one.

The methods of arranging or selecting a small or equal number of people or items at a time from a group of people or items provided with due consideration to be arranged in order of planning or selection are called permutations.

Each different group or selection that can be created by taking some or all of the items, no matter how they are organized, is called a combination.

Basic Permutation (nPr formula) Examples

            Here We are making group of n different objects, selected r at a time equivalent to filling r places from n things.

The number of ways of arranging = The number of ways of filling r places.

ⁿP_r = n. (n-1). (n-2)…(n-r+1) = n/(n-r)!

so nPr formula we have to use is

ⁿP_r = n!/(n-r)!

Example 1): There is a train whose 7 seats are kept empty, then how many ways can three passengers sit.

solution: Here n=7, r=3

so      Required number of ways=

ⁿP_r = n!/(n-r)!

⁷P₃ = 7!/(7-3)! = 4!.5.6.7/4! = 210

In 210 ways 3 passengers can sit.

Example 2) How many ways can 4 people out of 10 women be chosen as team leaders?

solution: Here n=10, r=4

so      Required number of ways=

ⁿP_r = n!/(n-r)!

¹⁰P₄ = 10!/(10-4)! = 6!7.8.9.10/6! = 5040

In 5040 ways 4 women can be chosen as team leaders.

Example 3) How many permutations are possible from 4 different letter, selected from the twenty-six letters of the alphabet?

solution: Here n=26, r=4

so      Required number of ways=

ⁿP_r = n!/(n-r)!

²⁶P₄ = 26!/(26-4)! = 22!.23.24.25.26/22! = 358800

In 358800 ways, 4 different letter permutations are available.

Example 4) How many different three-digit permutations are available, selected from ten digits from 0 to 9 combined?(including 0 and 9).

solution: Here n=10, r=3

so      Required number of ways=

ⁿP_r = n!/(n-r)!

¹⁰P₃ = 10!/(10-3)! = 7!.8.9.10/7! = 720

In 720 ways, three-digit permutations are available.

Example 5) Find out the number of ways a judge can award a first, second, and third place in a contest with 18 competitors.

solution: Here n=18, r=3

so      Required number of ways=

ⁿP_r = n!/(n-r)!

¹⁸P₃ = 18!/(18-3)! = 15!.16.17.18/15! = 4896

Among the 18 contestants, in 4896 number of ways, a judge can award a 1st, 2nd and 3rd place in a contest.

Example

6) Find the number of ways, 7 people can organize themselves in a row.

solution: Here n=7, r=7

so      Required number of ways=

ⁿP_r = n!/(n-r)!

⁷P₇ = 7!/(7-7)! = 7!/0! = 5040

In 5040 number of ways, 7 people can organize themselves in a row.

Examples based on Combination (nCr formula/ n choose k formula)

The number of combinations (selections or groups) that can be set up from n different objects taken r (0<=r<=n) at a time is

This is commonly known as nCr or n choose k formula.

ⁿC_k = n!/k!(n-k)!

Examples:

1) If you have three dress with different colour in red, yellow and white then can you find a different combination you get if you have to choose any two of them?

Solution: here n=3, r=2 this is 3 CHOOSE 2 problem

ⁿC_r = n!/r!(n-r)!

³C₂ = 3!/2!(3-2)! = 2!.3/2!.1 = 3

In 3 different combination you get any two of them.

2) How many different combinations can be done if you have 4 different items and you have to choose 2?

Solution: here n=4, r=2 this is 4 CHOOSE 2 problem

ⁿC_r = n!/r!(n-r)!

⁴C₂ = 4!/2!(4-2)! = 2!.3.4/2!.2! = 6

In 6 different combination you get any two of them.

3) How many different combinations can be made if you have only 5 characters and you have to choose any 2 among them?

Solution: here n=5, r=2 this is 5 CHOOSE 2 problem

ⁿC_r = n!/r!(n-r)!

⁵C₂ = 5!/2!(5-2)! = 3!.4.5/2!.3! = 10

In 10 different combination you get any two of them.

4) Find the number of combinations 6 choose 2.

Solution: here n=6, r=2 this is 6 CHOOSE 2 problem

ⁿC_r = n!/r!(n-r)!

⁶C₂ = 6!/2!(6-2)! = 4!.5.6/2!.4! = 15

In 15 different combination you get any two of them.

5) Find the number of ways of choosing 3 members from 5 different partners.

Solution: here n=5, r=3 this is 5 CHOOSE 3 problem

ⁿC_r = n!/r!(n-r)!

⁵C₃ = 5!/3!(5-3)! = 3!.4.5/3!.2! = 10

In 10 different combination you get any three of them.

6) Box of crayons having red, blue, yellow, orange, green and purple. How many unlike ways can you use to draw only three colour?

Solution: here n=6, r=3 this is 6 CHOOSE 3 problem

ⁿC_r = n!/r!(n-r)!

⁶C₃ = 6!/3!(6-3)! = 3!.4.5.6/3!.3.2.1 =20

In 20 different combination you get any three of them.

7) Find the number of combinations for 4 choose 3.

Solution: here n=4, r=3 this is 4 CHOOSE 3 problem

ⁿC_r = n!/r!(n-r)!

⁴C₃ = 4!/3!(4-3)! = 3!.4/ 3!.1! = 4

In 4 different combination you get any three of them.

8) How many different five-person committees can be elected from 10 people?

Solution: here n=10, r=5 this is 10 CHOOSE 5 problems

ⁿC_r = n!/r!(n-r)!

¹⁰C₅ = 10!/5!(10-5)! = 10!/5!.5! = 5!.6.7.8.9.10/5!.5.4.3.2 = 7.4.9 =252

So 252 different 5 person committees can be elected from 10 people.

9) There are 12 volleyball players in total in college, which will be made up of a team of 9 players. If the captain remains consistent, the team can be formed in how many ways.

Solution: here as the captain already has been selected, so now among 11 players 8 are to be chosen n=11, r=8 this is 11 CHOOSE 8 problem

ⁿC_r = n!/r!(n-r)!

¹¹C₈ = 11!/8!(11-8)! = 11!/8!.3! = 8!.9.10.11/8!.3.2.1 = 3.5.11 = 165

So If the captain remains consistent, the team can be formed in 165 ways.

10) Find the number of combinations 10 choose 2.

Solution: here n=10, r=2 this is 10 CHOOSE 2 problem

ⁿC_r = n!/r!(n-r)!

¹⁰C₂ = 10!/2!(10-2)! = 10!/2!.8! = 8!.9.10/2!.8! = 5.9 = 45

In 45 different combination you get any two of them.

We have to see the difference that nCr is the number of ways things can be selected in ways r and nPr is the number of ways things can be sorted by means of r. We have to keep in mind that for any case of permutation scenario, the way things are arranged is very very important. However, in Combination, the order means nothing.

Conclusion

A detailed description with examples of the Permutations and combinations has been provided in this article with few real-life examples, in a series of articles we will discuss in detail the various outcomes and formulas with relevant examples if you are interested in further study go through this link.

Reference

1. SCHAUM’S OUTLINE OF Theory and Problems of DISCRETE MATHEMATICS
2. https://en.wikipedia.org/wiki/Permutation
3. https://en.wikipedia.org/wiki/Combination

Permutations and Combinations

 Permutations and Combinations, this article will discuss the concept of determining, in addition to the direct calculation, the number of possible outcomes of a particular event or the number of set items, permutations and combinations that are the primary method of calculation in combinatorial analysis.

Common mistakes while learning Permutations and Combinations

There is always confusion amongst the student between permutations and combinations because both are related to the number of the arrangement of different objects and the number of the possible outcome of a particular event or number of ways to get an element from a set. The topic of permutation & combination with examples and the difference between them with justification will be discussed here.

A simple and handy technique to remember the difference between the permutations and combinations is: a permutation is related with the order means the position is important in permutation while the combination is not related with the order means the position is not important in combination.

Before the discussion of permutations and combinations, we require some prerequisites, which are frequently used.

 What is Factorial

          Factorial is the product of the positive integers from 1 to n (counting 1 and n) denoted by n! and read as n factorial is described as below

n! = 1.2.3.4… (n-2).(n-1).n = n.(n-1).(n-2)…3.2.1

ⁿP_r = n.(n-1).(n-2)…(n–r+1) = n!/(n-r)!

Mind it 0!=1 

0! = 1

1! = 1

n! = n(n-l)!

e.g 3! = 3.2.1 = 6

4! = 4.3.2.1 = 24

5! = 5.4! = 5.24 = 120

Counting Methods (Principle of Multiplication and addition)

      Principle of addition: If no two events can happen at the same time, then one of the events can happen in

n1  + n2  + n3  +・ ・ ・.ways

      Principle of Multiplication: Considering that if the events occurred one after the other, then all the events can happen in the order indicated in:

n₁.n₂.n₃…ways

Example: If an Institute runs 7 different art courses, 3 different technical courses, and 4 different physical courses.

If a student wants to enroll one of each type of course then the number of ways would be

m=7.3.4=84

If a student wants to enroll just one of the courses, then the number of ways would be

n=7 + 3 + 4=14

What is Permutation

The different positioning of the objects are called Permutations, where the order of the arrangement matters. Any positioning of a set of n different objects in a given order is called a permutation of the object.

        Consider an example of the set of letters {P,Q,R,S}, then

  Some of the permutations of the four alphabets taken 4 at a glance are QSRP, SRQP and PRSQ

Any ordering of any r<=n of these particular objects in a specific order is called an “r-permutation” or “a permutation of the n objects taken r at a time.

Basically we like those number of such permutations without set down them.

Example of Permutation Formula

The number of permutations of n different objects taken r at a time will be indicated by

ⁿP_r = n. (n-1).(n-2)…(n-r+1) = n!/(n–r)!

In mathematics this is denoted by different ways, some of them are mentioned below:

P(n,r), nPr,Pn,r ,or (n)r

EXAMPLE: Calculate the number m of permutations of six objects, say A, B, C, D, E, F taken three at a glance.

Solution:   Here n=6, r=3, m=?

ⁿP_r = n!/(n-r)!

m = ⁶P₃ = 6!/(6-3)! = 6!/3! = 3!.4.5.6/3!= 4.5.6 = 120

So m=120

EXAMPLE: How many words can be generated by using 2 letters from the word “MATHS”?

Solution: Here n=5, r=2, m=?

ⁿP_r = n!/(n-r)!

m = ⁵P₂ = 5!/(5-2)! = 5!/3! = 3!.4.5/3! = 4.5 = 20

so the required number of words are 20.

What do you understand by a Combination?

A combination for n different elements taken r at a time is any selection of r-th elements where orders are not being considered. Such a selection is called an r-combination. In brief, a Combination is a selection in which the order of the objects selected is not important.

      The Combination gives the number of ways a particular set can be arranged, where the order of the arrangement does not matter.

 To understand the situation of Combination, consider the example

Twenty people arrive in a hall and everyone shakes hand with all the others. How can we get the number of handshakes?  “A” shaking hands with B and B with A will not be two different handshakes. Here, the order of handshake is not important. The number of handshakes will be the combinations of 20 different things taken 2 at a time.

Combination Formula with a simple example

       The number of such combinations will be denoted by

Sometimes it is also denoted by C(n,r), ⁿC_r , C_n,r or C_rⁿ

Example: A class contains 10 students with 6 men and 4 women. Find the number n of ways to choose a 4-member committee among those students.

This is related to combinations, not permutations, since order is not an important factor in a committee. There are “10 choose 4” such committees. That is:

here n=10, r= 4

so in 210 ways we can choose such 4-member committee.

Example: A container has 6 blue balls and 8 red balls. Identify the number of ways two balls of any of the colors can be drawn from the container.

Here possibly “14 choose 2” ways for selecting 2 of the 14 balls. Thus:

Here n=14 , r=2

so in 91 ways two balls can be drawn of any color.

Difference between Permutation and Combination

The difference between permutation vs combination is briefly given here

Where to apply Permutations and Combinations

  This is the important step that should be kept in mind that whenever the situation is for arrangement, ordering and uniqueness we have to use Permutation and whenever the situation is  for selection, choosing, picking and combination without the concern of order we have to use Combination. If you keep these basics in your mind there will be no confusion “what to use and what not” whenever a question arises.

Use of Permutations and Combinations in real life with examples

In real life permutation and the combination is used in almost everywhere because we know that in real life there would be a situation when order is important and somewhere order is not important, in those situations we have to use the corresponding method.

For example

Find the number N of teams of 11 with a given captain that can be selected from 26 players.

Frequently Asked Questions – FAQs

What is factorial?

The product of the positive integers from  1 to n (including 1 & n )

n! = 1.2.3… (n-2). (n-1). n

What is a permutation?

The different ordering of the objects are called Permutations

What is a Combination?

     The Combination provides the number of ways a specific set can be set out, where the order of the arrangement does not matter.

Application of permutations and combinations in practical life

A Permutation is used for arrangement or selection of lists where the order is important, and Combination is used for selection or choice where the order is not important.

Permutation formula

ⁿP_r = n!/(n-r)!

Combination formula

Is there any relation between permutations and Combinations?

Yes,

ⁿC_r = ⁿP_r/r!

Can we use Permutations and combinations in real life?

Yes,

In the arrangement of words, alphabets, numbers, positions and colours etc. where the order is important permutation will be used

In the selection of committee, teams, menu, and subjects etc where the order is not important combination will be used.

   The brief information about permutations and combinations with basic formula is given read twice or thrice till you get the idea about the concept, in consecutive articles we will discuss in detail the different results and formulae with suitable examples of permutations and combinations. If you want further study go through:

For more Topics on Mathematics, please follow this link.

References:

1.   SCHAUM’S OUTLINE OF Theory and Problems of DISCRETE MATHEMATICS

2.   https://en.wikipedia.org/wiki/Permutation

3.   https://en.wikipedia.org/wiki/Combination

4.   https://in.bgu.ac.il/

5.   https://www.cs.bgu.ac.il/