How to Find Tension to Torque
Tension and torque are two important concepts in physics and engineering. Understanding the relationship between tension and torque can help us solve various problems in mechanics and design. In this blog post, we will explore how to calculate tension using torque, find tension in a pulley system, determine tension force between two objects, and calculate tension with mass and velocity. So, let’s dive in!
Understanding the Basics of Tension and Torque
Before we delve into the calculations, let’s quickly refresh our knowledge on tension and torque. Tension refers to the force transmitted through a string, cable, or any other type of flexible connector. It acts along the length of the connector and is always directed away from the object exerting the force.
On the other hand, torque is the rotational force or moment that tends to cause an object to rotate around an axis. It is the product of the force applied and the distance from the axis of rotation. Torque is usually measured in units of Newton-meters (Nm).
The Relationship between Tension and Torque
The relationship between tension and torque comes into play when dealing with systems that involve rotational motion or objects connected by flexible connectors. In such systems, the tension in the connectors can be determined using torque.
When a flexible connector is subjected to torque, it experiences a tension force that resists the rotational motion. The magnitude of this tension force can be calculated using the following formula:
![]()
where: – T is the tension force – T_{\text{Torque}} is the torque applied – r is the radius or distance from the axis of rotation
The formula tells us that tension is directly proportional to torque and inversely proportional to the radius. As the torque increases, the tension in the connector also increases. Similarly, if the radius decreases, the tension increases.
Now that we have a basic understanding of tension and torque, let’s move on to calculating tension using torque.
Calculating Tension Using Torque
Understanding the Torque Tension Formula
To calculate tension using torque, we can rearrange the tension formula as follows:
![]()
This formula allows us to find the tension force by multiplying the torque by the reciprocal of the radius.
Step-by-Step Guide on How to Calculate Tension from Torque
To calculate tension using torque, follow these steps:
- Determine the torque applied to the system or connector.
- Measure the radius or distance from the axis of rotation.
- Plug the values into the tension formula
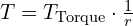 .
. - Calculate the tension force.
Let’s work through an example to illustrate this process.
Worked Out Examples on Calculating Tension Using Torque

Example 1: Suppose we have a system where a torque of 20 Nm is applied, and the radius is 1 meter. We want to find the tension in the connector.
Solution:
Using the tension formula, ![]() , we can substitute the given values:
, we can substitute the given values:
![]()
Therefore, the tension in the connector is 20 N.
Example 2: Let’s consider another scenario where the torque applied is 30 Nm, and the radius is 0.5 meters. Find the tension in the connector.
Solution:
Using the tension formula, ![]() , we can substitute the given values:
, we can substitute the given values:
![]()
Therefore, the tension in the connector is 60 N.
By following this step-by-step guide and working through examples, you can easily calculate tension using torque. This method is particularly useful in mechanical engineering, where understanding the tension in connectors is essential for designing safe and reliable systems.
Finding Tension in a Pulley System
The Role of Torque in a Pulley System
In a pulley system, tension plays a crucial role in transferring forces and enabling the system to function properly. Torque is directly related to tension in a pulley system. The tension force in a pulley system can be determined by considering the torque acting on the pulley.
How to Calculate Tension in a Pulley Using Torque
To calculate the tension in a pulley system using torque, we need to consider the following:
- Identify the torque acting on the pulley.
- Determine the radius of the pulley.
- Use the tension formula
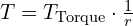 to find the tension.
to find the tension.
Let’s work through an example to illustrate this process.
Worked Out Examples on Finding Tension in a Pulley System

Example 1: Suppose we have a pulley system with a torque of 15 Nm acting on the pulley. The radius of the pulley is 0.8 meters. Find the tension in the system.
Solution:
Using the tension formula, ![]() , we can substitute the given values:
, we can substitute the given values:
![]()
Therefore, the tension in the pulley system is approximately 18.75 N.
Example 2: Consider another pulley system where the torque applied is 25 Nm, and the radius is 0.6 meters. Calculate the tension in the system.
Solution:
Using the tension formula, ![]() , we can substitute the given values:
, we can substitute the given values:
![]()
Therefore, the tension in the pulley system is approximately 41.67 N.
By following these steps and working through examples, you can easily find the tension in a pulley system using torque. This knowledge is valuable in various applications, such as designing mechanical systems or analyzing the performance of pulley-based mechanisms.
Determining Tension Force between Two Objects
The Role of Torque in Tension Force
When two objects are connected by a flexible connector, such as a rope or cable, the tension force in the connector is essential for maintaining equilibrium. Torque plays a vital role in determining the tension force between two objects.
How to Calculate Tension Force Using Torque
To calculate the tension force between two objects using torque, follow these steps:
- Identify the torque acting on the system.
- Determine the relevant radii or distances involved.
- Use the tension formula
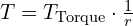 to find the tension force.
to find the tension force.
Let’s work through an example to illustrate this process.
Worked Out Examples on Determining Tension Force
Example 1: Suppose we have two objects connected by a flexible connector. The torque acting on the system is 12 Nm, and the radius is 0.4 meters. Calculate the tension force between the objects.
Solution:
Using the tension formula, ![]() , we can substitute the given values:
, we can substitute the given values:
![]()
Therefore, the tension force between the two objects is 30 N.
Example 2: Consider another scenario where the torque applied is 18 Nm, and the radius is 0.5 meters. Determine the tension force between the objects.
Solution:
Using the tension formula, ![]() , we can substitute the given values:
, we can substitute the given values:
![]()
Therefore, the tension force between the two objects is 36 N.
By following these steps and working through examples, you can easily determine the tension force between two objects using torque. This knowledge is valuable in various fields, including physics, engineering, and mechanical design.
Finding Tension with Mass and Velocity
Understanding the Relationship between Mass, Velocity, and Torque
In some cases, we may need to calculate tension based on the mass and velocity of an object in motion, along with torque. The relationship between mass, velocity, and torque is crucial for solving such problems.
How to Calculate Tension with Mass and Velocity Using Torque
To calculate tension with mass and velocity using torque, follow these steps:
- Determine the mass of the object in motion.
- Calculate the velocity of the object.
- Identify the torque acting on the system.
- Use the tension formula
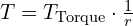 to find the tension.
to find the tension.
Let’s work through an example to illustrate this process.
Worked Out Examples on Finding Tension with Mass and Velocity
Example 1: Suppose we have an object with a mass of 2 kg moving at a velocity of 5 m/s. The torque acting on the system is 8 Nm, and the radius is 0.3 meters. Find the tension in the system.
Solution: To calculate tension with mass and velocity, we first need to find the torque using the following formula:
![]()
Substituting the given values:
![]()
Now, using the tension formula, ![]() , we can substitute the torque and radius values:
, we can substitute the torque and radius values:
![]()
Therefore, the tension in the system is approximately 166.67 N.
Example 2: Consider another scenario where an object with a mass of 4 kg is moving at a velocity of 3 m/s. The torque applied is 10 Nm, and the radius is 0.4 meters. Calculate the tension in the system.
Solution:
Using the formula to find the torque, ![]() , we can substitute the given values:
, we can substitute the given values:
![]()
Next, using the tension formula, ![]() , we can substitute the torque and radius values:
, we can substitute the torque and radius values:
![]()
Therefore, the tension in the system is 90 N.
By following these steps and working through examples, you can easily find the tension with mass and velocity using torque. This knowledge is valuable in various applications, including analyzing the tension in moving systems or designing mechanisms involving rotational motion.
Numerical Problems on how to find tension to torque
Problem 1:

A cable with a tension of 500 N is wrapped around a drum with a radius of 0.2 m. What is the torque exerted on the drum by the tension in the cable?
Solution:
Given:
Tension, ![]() Radius of the drum,
Radius of the drum, ![]()
The torque exerted by the tension on the drum can be calculated using the formula:
![]()
Substituting the given values, we have:
![]()
Therefore, the torque exerted on the drum by the tension in the cable is 100 Nm.
Problem 2:
A rope is wrapped around a pulley with a radius of 0.5 m. If a tension of 800 N is applied to the rope, what is the torque exerted on the pulley?
Solution:
Given:
Tension, ![]() Radius of the pulley,
Radius of the pulley, ![]()
The torque exerted by the tension on the pulley can be calculated using the formula:
![]()
Substituting the given values, we have:
![]()
Therefore, the torque exerted on the pulley by the tension in the rope is 400 Nm.
Problem 3:
A wrench is used to apply a torque of 120 Nm to a bolt. If the length of the wrench handle is 0.3 m, what is the tension in the wrench?
Solution:
Given:
Torque, ![]() Length of the wrench handle,
Length of the wrench handle, ![]()
The tension in the wrench can be calculated using the formula:
![]()
Substituting the given values, we have:
![]()
Therefore, the tension in the wrench is 400 N.

I am Sangeeta Das. I have completed my Masters in Mechanical Engineering with specialization in I.C Engine and Automobiles. I have around ten years of experience encompassing industry and academia. My area of interest includes I.C. Engines, Aerodynamics and Fluid Mechanics. You can reach me at