What Does the Magnitude of the Acceleration Mean?

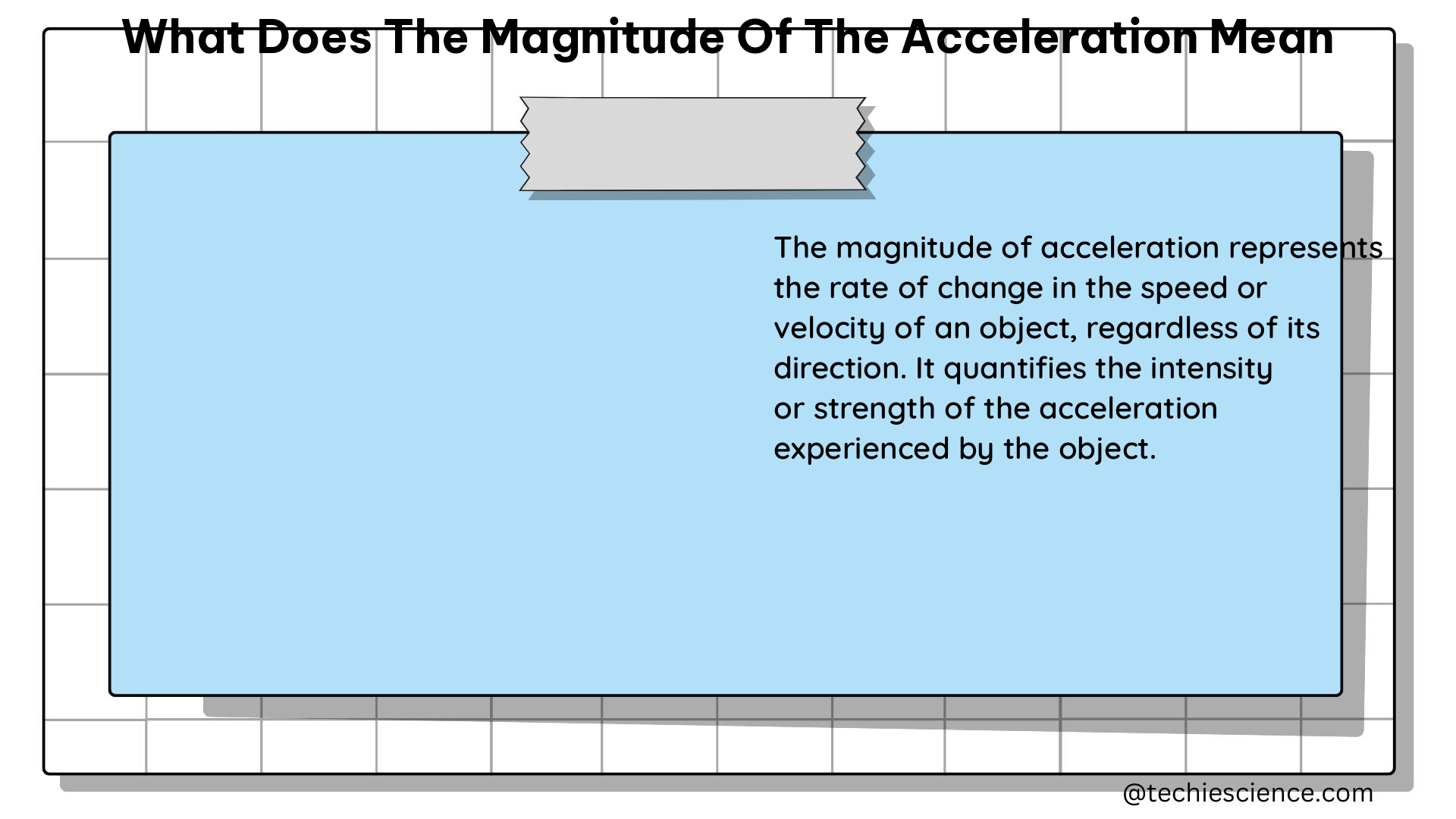
The magnitude of acceleration is a fundamental concept in physics that represents the rate of change in velocity, regardless of the direction of movement. It is a measure of how quickly the velocity of an object changes over a given unit of time. Understanding the magnitude of acceleration is crucial for analyzing and predicting the motion of objects in various physical systems, from everyday situations to complex scientific and engineering applications.

Understanding Acceleration and Its Magnitude

Acceleration is a vector quantity, meaning it has both a magnitude (numerical value) and a direction. The magnitude of acceleration, denoted as |a|, represents the rate of change in the speed or velocity of an object. It is calculated as the change in velocity divided by the change in time, or mathematically expressed as:

|a| = Δv / Δt

where Δv is the change in velocity and Δt is the change in time.

The magnitude of acceleration can be positive or negative, depending on whether the object is speeding up or slowing down. For example, if a car is accelerating from 0 to 60 miles per hour (mph) in 10 seconds, the magnitude of its acceleration would be 6 mph/s (or 2.68 m/s²). Conversely, if the car is decelerating from 60 mph to 0 mph in 10 seconds, the magnitude of its acceleration would be -6 mph/s (or -2.68 m/s²).

Calculating the Magnitude of Acceleration

The magnitude of acceleration can be calculated using the formula:

|a| = |F| / m

where |a| is the magnitude of acceleration, |F| is the magnitude of the net force acting on the object, and m is the mass of the object.

This formula is derived from Newton’s second law of motion, which states that the net force acting on an object is equal to the product of the object’s mass and its acceleration. Rearranging this equation, we can solve for the magnitude of acceleration:

|a| = |F| / m

This formula is particularly useful when analyzing the motion of objects under the influence of various forces, such as gravity, friction, or applied forces.

Examples of Magnitude of Acceleration

1. Free Fall: When an object is dropped near the Earth’s surface, it experiences acceleration due to gravity, which has a magnitude of approximately 9.8 m/s² (or 32.2 ft/s²) directed downward.

2. Braking: When a car applies its brakes, the magnitude of its acceleration is negative, representing the deceleration of the vehicle. The magnitude of this acceleration can be calculated using the formula above, considering the net force applied by the brakes and the mass of the car.

3. Circular Motion: An object moving in a circular path experiences centripetal acceleration, which has a magnitude that depends on the object’s velocity and the radius of the circular path. The magnitude of this acceleration can be calculated using the formula: |a| = v²/r, where v is the object’s velocity and r is the radius of the circular path.

4. Projectile Motion: When an object is launched into the air, such as a ball or a rocket, it experiences a combination of horizontal and vertical accelerations. The magnitude of the vertical acceleration is typically the acceleration due to gravity, while the horizontal acceleration may be influenced by factors such as air resistance or propulsive forces.

5. Elevator Acceleration: When an elevator starts moving, the passengers inside experience a temporary increase in their apparent weight due to the acceleration of the elevator. The magnitude of this acceleration can be calculated using the formula above, considering the net force acting on the elevator and its mass.

Numerical Problems and Calculations

1. A car is traveling at a constant speed of 60 mph. If the car suddenly applies its brakes and comes to a complete stop in 5 seconds, what is the magnitude of the car’s acceleration during the braking process?

Given:
– Initial velocity (v₀) = 60 mph
– Final velocity (v) = 0 mph
– Time (t) = 5 seconds

To calculate the magnitude of acceleration, we can use the formula:
|a| = Δv / Δt
Δv = v – v₀ = 0 – 60 = -60 mph
Δt = 5 seconds

Substituting the values, we get:
|a| = Δv / Δt
|a| = -60 mph / 5 s
|a| = -12 mph/s

1. A ball is thrown vertically upward with an initial velocity of 20 m/s. Assuming the acceleration due to gravity is 9.8 m/s², what is the magnitude of the ball’s acceleration at the highest point of its trajectory?

Given:
– Initial velocity (v₀) = 20 m/s
– Acceleration due to gravity (g) = -9.8 m/s²

At the highest point of the trajectory, the ball’s velocity is momentarily zero (v = 0 m/s). Using the kinematic equation:
v = v₀ + at
0 = 20 + (-9.8)t
t = 2.04 s

Substituting the time into the kinematic equation:
a = (v – v₀) / t
a = (0 – 20) / 2.04
a = -9.8 m/s²

The magnitude of the ball’s acceleration at the highest point is 9.8 m/s².

Conclusion

The magnitude of acceleration is a crucial concept in physics that represents the rate of change in velocity, regardless of the direction of movement. It is a scalar quantity that can be calculated using the formula |a| = |F|/m, where |a| is the magnitude of acceleration, |F| is the magnitude of the force, and m is the mass of the object. Understanding the magnitude of acceleration is essential for analyzing and predicting the motion of objects in various physical systems, from everyday situations to complex scientific and engineering applications.

References:

1. Acceleration – Wikipedia
2. Magnitude of Acceleration – Physics Classroom
3. Calculating Acceleration – Khan Academy
4. Acceleration Formulas and Equations – Physicsabout.com