Summary
Water density is a crucial physical property that varies with temperature and the presence of dissolved substances. Pure water has a density of approximately 1 g/cm³ at 4°C, but this value can change significantly depending on factors such as temperature and salinity. Understanding and accurately measuring water density is essential in various scientific, engineering, and industrial applications, from oceanography and hydrology to chemical processing and water treatment.
Table of Contents
- Introduction to Water Density
- Factors Affecting Water Density
- Temperature
- Salinity and Dissolved Substances
- Pressure
- Theoretical Aspects of Water Density
- Molecular Structure and Intermolecular Forces
- Density Anomaly of Water
- Equation of State for Water
- Measuring Water Density
- Laboratory Equipment and Techniques
- Density Measurement Methods
- Accuracy and Precision Considerations
- Practical Applications of Water Density
- Oceanography and Marine Science
- Hydrology and Water Resource Management
- Chemical Processing and Water Treatment
- Buoyancy and Flotation
- Numerical Examples and Problem-Solving
- Calculating Water Density Given Temperature and Salinity
- Determining Volume or Mass from Density Measurements
- Solving Buoyancy-Related Problems
- Data and Empirical Correlations
- Density of Pure Water as a Function of Temperature
- Density of Seawater as a Function of Temperature and Salinity
- Density of Other Water-Based Solutions
- Conclusion
1. Introduction to Water Density
Water density is a fundamental physical property that describes the mass of water per unit volume. It is typically expressed in units of grams per cubic centimeter (g/cm³) or kilograms per cubic meter (kg/m³). The density of water is an essential parameter in various scientific and engineering applications, as it affects the behavior and properties of water-based systems.
2. Factors Affecting Water Density
2.1 Temperature
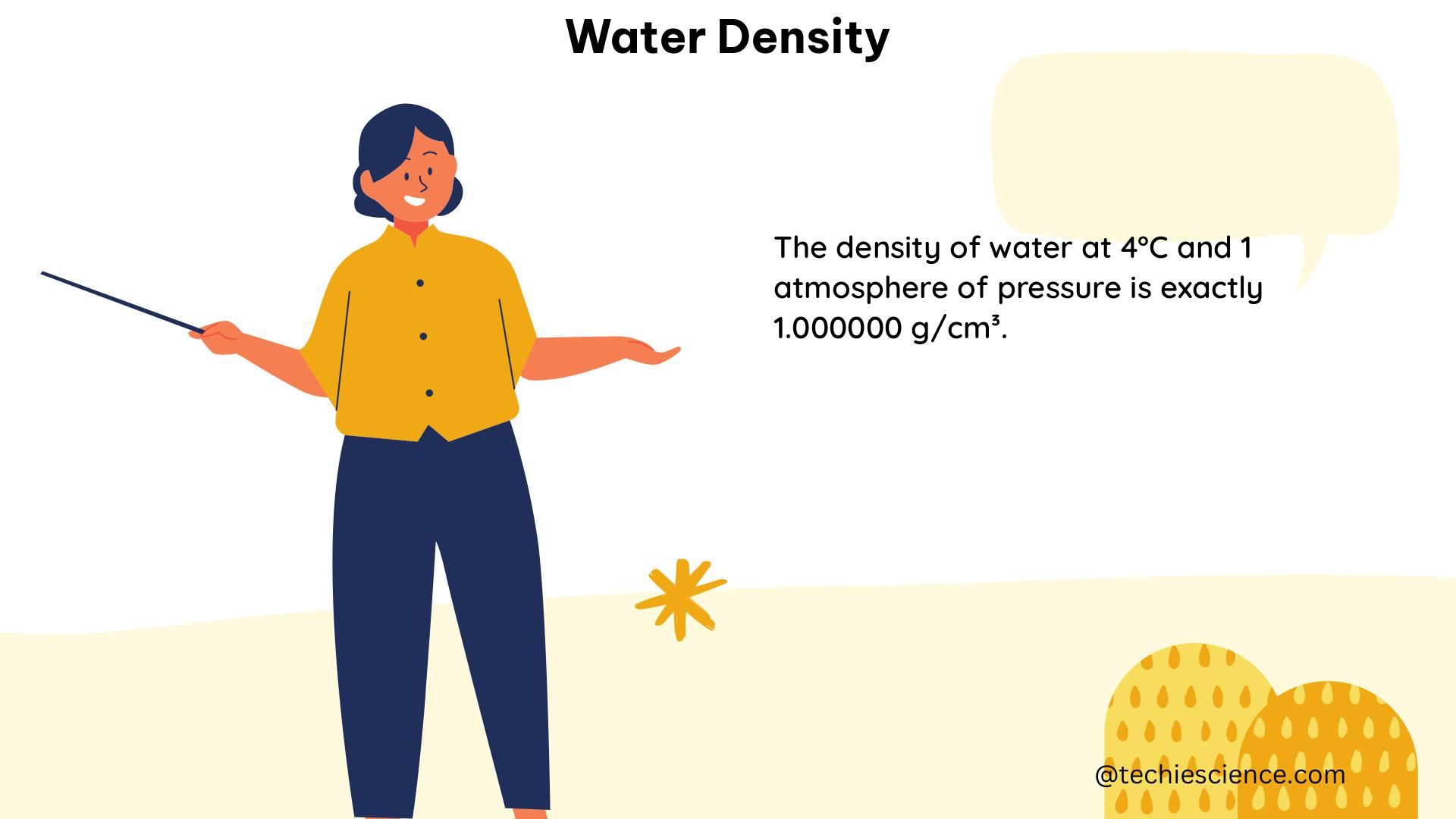
The density of water is highly dependent on temperature. At standard atmospheric pressure, the density of pure water reaches its maximum value of approximately 1.000 g/cm³ at 4°C (39.2°F). As the temperature increases or decreases from this point, the density of water decreases. This phenomenon is known as the “density anomaly of water” and is a unique characteristic of this substance.
The relationship between water density and temperature can be expressed by the following equation:
ρ = 1 - (T - 4)^2 / (508 × (T + 16.5))
where ρ is the density of water in g/cm³ and T is the temperature in degrees Celsius (°C).
2.2 Salinity and Dissolved Substances
The presence of dissolved substances, such as salts, in water can significantly affect its density. Seawater, for example, has a higher density than freshwater due to the dissolved salts, primarily sodium chloride (NaCl). The density of seawater can be calculated using the following empirical formula:
ρ = 1.0 + 0.0008 × S
where ρ is the density of seawater in g/cm³ and S is the salinity in parts per thousand (ppt).
2.3 Pressure
The density of water also varies with pressure, although the effect is relatively small compared to the influence of temperature and salinity. As depth increases in a body of water, the pressure also increases, leading to a slight increase in water density. This relationship can be described by the following equation:
ρ = ρ₀ × (1 + 0.000043 × P)
where ρ is the density of water at the given pressure, ρ₀ is the density of water at standard atmospheric pressure (1 atm), and P is the pressure in atmospheres (atm).
3. Theoretical Aspects of Water Density
3.1 Molecular Structure and Intermolecular Forces
The density of water is closely related to its molecular structure and the intermolecular forces between water molecules. Water molecules are composed of one oxygen atom and two hydrogen atoms, with a tetrahedral arrangement of the atoms. The unique polarity of the water molecule and the hydrogen bonding between adjacent molecules contribute to the high density of water compared to other liquids.
3.2 Density Anomaly of Water
The density anomaly of water refers to the fact that the density of water reaches a maximum value at 4°C (39.2°F) under standard atmospheric pressure. This anomaly is due to the complex interplay between the hydrogen bonding and the thermal motion of water molecules. As the temperature increases or decreases from 4°C, the density of water decreases due to the disruption of the hydrogen bond network and the increased thermal motion of the molecules.
3.3 Equation of State for Water
The equation of state for water describes the relationship between the density, temperature, and pressure of water. One commonly used equation of state is the Kell equation, which is expressed as:
ρ = 999.83952 + 16.945176T - 7.9870401 × 10^-3T^2 - 46.170461 × 10^-6T^3 + 105.56302 × 10^-9T^4 - 280.54253 × 10^-12T^5
where ρ is the density of water in kg/m³ and T is the temperature in degrees Celsius (°C).
4. Measuring Water Density
4.1 Laboratory Equipment and Techniques
Measuring the density of water in a laboratory setting typically involves the use of various equipment, such as:
- Graduated cylinders or volumetric flasks for measuring the volume of water
- Analytical balances for accurately measuring the mass of water
- Density bottles or pycnometers for precise volume measurements
- Hydrometers or digital density meters for direct density measurements
The basic procedure for measuring water density involves the following steps:
- Measure the mass of an empty, clean, and dry container (e.g., graduated cylinder or pycnometer).
- Fill the container with a known volume of water, ensuring that the water temperature is stable and recorded.
- Measure the mass of the container filled with water.
- Calculate the density of the water using the formula
ρ = m/V, whereρis the density,mis the mass of the water, andVis the volume of the water.
4.2 Density Measurement Methods
In addition to the direct mass-volume method, there are other techniques for measuring the density of water, such as:
- Buoyancy method: Measuring the buoyant force exerted on an object immersed in water and using it to calculate the density.
- Displacement method: Measuring the volume of water displaced by a known mass of an object to determine the density.
- Hydrometer method: Using a calibrated hydrometer to directly measure the density of water or other liquids.
- Digital density meters: Employing electronic devices that use various principles, such as oscillating U-tube or vibrating plate, to measure the density of water.
4.3 Accuracy and Precision Considerations
When measuring the density of water, it is essential to consider factors that can affect the accuracy and precision of the measurements, such as:
- Temperature control: Ensuring that the water temperature is stable and accurately measured, as density is highly dependent on temperature.
- Impurities and dissolved substances: Using deionized or distilled water to minimize the presence of dissolved impurities that can alter the density.
- Calibration and equipment accuracy: Ensuring that the laboratory equipment, such as balances and volumetric glassware, are properly calibrated and within their specified accuracy ranges.
- Repeatability and statistical analysis: Performing multiple measurements and using statistical methods to determine the mean density and associated uncertainty.
5. Practical Applications of Water Density
5.1 Oceanography and Marine Science
Water density is a crucial parameter in oceanography and marine science. It is used to study ocean currents, water mass movements, and the vertical stratification of the ocean. Accurate measurements of water density, along with temperature and salinity, are essential for understanding and modeling ocean dynamics.
5.2 Hydrology and Water Resource Management
The density of water is important in hydrology and water resource management, as it affects the behavior and transport of water in natural and engineered systems. Understanding water density is crucial for applications such as groundwater flow, surface water modeling, and the design of water treatment and distribution systems.
5.3 Chemical Processing and Water Treatment
In chemical processing and water treatment industries, the density of water is a critical parameter for various operations, such as:
– Determining the concentration of dissolved solids or chemicals in water
– Monitoring the efficiency of water purification and desalination processes
– Optimizing the design and operation of equipment like pumps, pipes, and tanks
5.4 Buoyancy and Flotation
The density of water is a fundamental principle in understanding buoyancy and flotation. The ability of objects to float or sink in water is directly related to their density relative to the density of water. This principle has applications in ship design, submarine operations, and the study of aquatic organisms and their adaptations.
6. Numerical Examples and Problem-Solving
6.1 Calculating Water Density Given Temperature and Salinity
Example: Calculate the density of seawater with a salinity of 35 ppt at a temperature of 20°C.
Given:
– Salinity (S) = 35 ppt
– Temperature (T) = 20°C
Using the equation for the density of seawater:
ρ = 1.0 + 0.0008 × S
ρ = 1.0 + 0.0008 × 35
ρ = 1.028 g/cm³
6.2 Determining Volume or Mass from Density Measurements
Example: A graduated cylinder containing 50 mL of water has a mass of 53.45 g. Calculate the density of the water and the mass of 100 mL of the same water.
Given:
– Volume of water (V) = 50 mL
– Mass of water (m) = 53.45 g
Step 1: Calculate the density of the water.
Density (ρ) = Mass (m) / Volume (V)
ρ = 53.45 g / 50 mL
ρ = 1.069 g/cm³
Step 2: Calculate the mass of 100 mL of the same water.
Mass (m) = Density (ρ) × Volume (V)
m = 1.069 g/cm³ × 100 mL
m = 106.9 g
6.3 Solving Buoyancy-Related Problems
Example: A wooden block with a volume of 0.2 m³ has a mass of 150 kg. Calculate the buoyant force acting on the block when it is fully submerged in freshwater.
Given:
– Volume of the block (V) = 0.2 m³
– Mass of the block (m) = 150 kg
– Density of freshwater (ρ) = 1.000 g/cm³ = 1000 kg/m³
Step 1: Calculate the weight of the block.
Weight (W) = Mass (m) × Acceleration due to gravity (g)
W = 150 kg × 9.8 m/s² = 1470 N
Step 2: Calculate the buoyant force acting on the block.
Buoyant force (F_b) = Density of water (ρ) × Volume of the block (V) × Acceleration due to gravity (g)
F_b = 1000 kg/m³ × 0.2 m³ × 9.8 m/s² = 1960 N
The buoyant force acting on the block is 1960 N, which is greater than the weight of the block (1470 N). Therefore, the block will float in the freshwater.
7. Data and Empirical Correlations
7.1 Density of Pure Water as a Function of Temperature
The density of pure water as a function of temperature can be expressed by the following equation:
ρ = 999.83952 + 16.945176T - 7.9870401 × 10^-3T^2 - 46.170461 × 10^-6T^3 + 105.56302 × 10^-9T^4 - 280.54253 × 10^-12T^5
where ρ is the density of water in kg/m³ and T is the temperature in degrees Celsius (°C).
The following table shows the density of pure water at various temperatures:
| Temperature (°C) | Density (g/cm³) |
|---|---|
| 0 | 0.99984 |
| 4 | 1.00000 |
| 10 | 0.99973 |
| 20 | 0.99823 |
| 30 | 0.99567 |
| 40 | 0.99224 |
| 50 | 0.98804 |
| 60 | 0.98320 |
| 70 | 0.97777 |
| 80 | 0.97182 |
| 90 | 0.96540 |
| 100 | 0.95853 |
7.2 Density of Seawater as a Function of Temperature and Salinity
The density of seawater can be calculated using the following empirical formula:
ρ = 1.0 + 0.0008 × S
where ρ is the density of seawater in g/cm³ and S is the salinity in parts per thousand (ppt).
The following table shows the density of seawater with a salinity of 35 ppt at various temperatures:
| Temperature (°C) | Density (g/cm³) |
|---|---|
| 0 | 1.028 |
| 5 | 1.027 |
| 10 | 1.026 |
| 15 | 1.025 |
| 20 | 1.024 |
| 25 | 1.023 |
| 30 | 1.022 |
7.3 Density of Other Water-Based Solutions
The density of water-based solutions, such as aqueous salt solutions or organic-water mixtures, can be calculated using empirical correlations that take into account the concentration of the dissolved substances and the temperature.
For example, the density of a sodium chloride (NaCl) solution can be estimated using the following equation:
ρ = 1.0 + 0.7683 × C - 0.0926 × C^2 + 0.0053 × C^3
where ρ is the density of the NaCl solution in g/cm³ and C is the concentration of NaCl in molality (mol/kg).
Reference:
- Measuring the Density of Water – IU Pressbooks
- Density Measurement: All You Need to Know | METTLER TOLEDO
- Water Density | U.S. Geological Survey – USGS.gov
- Kell, G. S. (1975). Density, thermal expansivity, and compressibility of liquid water from 0° to 150°C: correlations and tables for atmospheric pressure and saturation reviewed and expressed on 1968 temperature scale. Journal of chemical and engineering data, 20(1), 97-105.
- [Millero, F. J., & Poisson, A. (1981). International one-atmosphere equation of state of seawater. Deep Sea Research Part A. Oceanographic Research Papers,

The lambdageeks.com Core SME Team is a group of experienced subject matter experts from diverse scientific and technical fields including Physics, Chemistry, Technology,Electronics & Electrical Engineering, Automotive, Mechanical Engineering. Our team collaborates to create high-quality, well-researched articles on a wide range of science and technology topics for the lambdageeks.com website.
All Our Senior SME are having more than 7 Years of experience in the respective fields . They are either Working Industry Professionals or assocaited With different Universities. Refer Our Authors Page to get to know About our Core SMEs.