The knowledge about Von Mises Stress Vs Principal Stress is highly effective to judge if a mechanical design is within design limits and will work safely during its operation period.
Principal stress on a plane is the maximum stress acts on it and in this case shear stress is measured as zero. Von Mises stress, mostly considered in case of a ductile material is a value used to determine the limit of fracture of a given material.
The equation to calculate Von Mises stress on a mechanical component
V = √(σx2 – (σx * σy) + σy2 + (3 *txy2))
Where V is the Von Mises Stress
σx is the normal stress x component
σy is the normal Stress y component
τxy is the Shear Stress
When a mechanical component is acted upon by 3D loads a very complex three dimensional stress system has developed. The direction and magnitude of stresses are different from point to point. Here Von Mises criterion is a formula for calculating the effect of these combined stresses at a point is responsible for failure or not.
Von Mises Stress Vs Principal Stress
Both Von Mises stress and Principal stress have owm significance in identifying the behaviour of a mechanical or structural component.
The differences between Von Mises and Principal stress are as follows:
| Principal Stress | Von Mises Stress |
| Principal stress is a real stress | A measure of energy density, not a real stress. |
| Principal stress represents the maximum and minimum of normal stresses on a principal plane at a condition of zero shear stress acts on a body. | Von Mises stress is associated with yielding criterion of a ductile material . Von Mises stress is a theoretical measurement and +ve or –ve sign depends on the principal stress. |
| Failure theory based on Principal stress is applicable to brittle materials like casting components, for example gear box. | Failure theory bases on Von Mises is used for ductile materials like aluminium, steel etc. |
| Not possible to calculate Principal stresses from Von Mises. | Possible to calculate Von Mises easily from Principal stresses. |
The normal stresses act on a principal plane are called Principal stresses which give the extreme values.If we consider two dimensional stress state of a material major and minor principal stresses will give the extreme values of the normal stresses.
Principal stresses can be obtained by rotating suitably the stress element in such a way that the rotated element does not experience any shear stress.
Engineers most widely use distortion energy theory to predict the failure of a ductile material and this theory also gives the perception of Von Mises stress.
Von Mises stress is not a true stress but a theoretical value which gives a comparison in between general tri dimensional stress and uni axial stress yield limit.
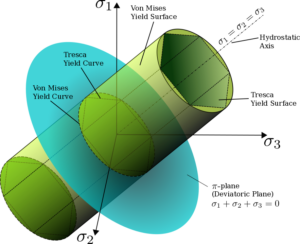
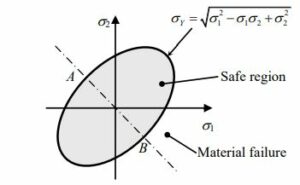
The above figure shows the yield criterion in the principal stress space. Any stress state can be represented by three principal stresses and considering as three coordinates, the various combinations of Von Mises stress may lead to a cylindrical surface.
The failure or yielding of a mechanical component starts at a point if the stress state associated with any point lies on the cylindrical surface.
Can Principal Stress be Greater than Von Mises?
In certain cases, the principal stresses are greater than Von Mises stress.
Von Mises sress can be expressed using the principal stresses acting in different axis as below:
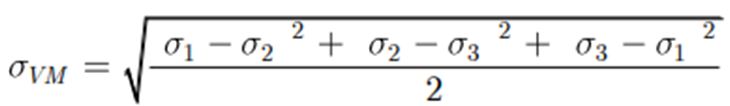
In certain conditions, principal stresses attains a greater value than the Von Mises stress. If Compression stresses which are acting on principal axes are nearly equal then Von Mises stresses will be very less.
Two types of failure are generally observed in Engineering materials: Brittle failure and Ductile failure.
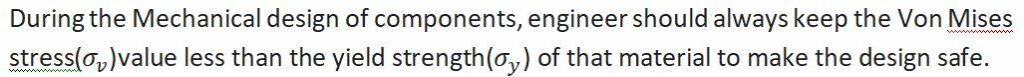
For the safe designing of piping and structural beams Von Mises stress theory is applied under various load condition.
The strength of a material is nothing but the necessary stress for breaking the atomic bond and splitting all the atoms of a material.
Ductile materials fail due to yielding and it happens due to the sliding of atoms. The necessary energy to yield is lower than the energy necessary for untying the atomic planes.
When the shear stress of a ductile material reaches its highest value(maximum), the yielding of the ductile material starts.
In case of brittle material the separation of atomic planes lead to failure of the material.
The strain energy density experienced at a point of a material can be expressed in terms of principal stresses as given below:
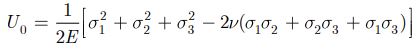
The strain energy density observed at a point in a material are mainly due to change in volume(Uh) and due to change in shape (Ud)which are popularly known as Dilatational and Distortion strain energy density respectively.
By substracting Uh i.e Dilatational Strain energy density from U0 i.e total energy density we will get Distortion strain energy(Ud) part.
The expression for Ud in terms of Von Mises stress can be written as below:
In the above formula, Ud is the distortion energy density and when it reaches a critical value, the yielding of ductile material begins. This idea is given by Von Mises theory.
Since this is generally applicable for an uniaxial stress state, we can easily calculate this critical value of distortional energy from uniaxial test.
Under this condition, the principal stress is given by σ1 = σY(yield stress) and and σ2 = σ3 = 0.
The necessary energy density for yielding is given below:
The above expression for energy density gives the the critical value of the distortional energy density for the material.
As per the Von Mises’s failure criterion, When a material is subjected to multiaxial loading, yielding of the material takes place when the distortional energy = or > than the critical value for the material.
Therefore, the yielding of a material starts when the Von Mises stresses acting on the material are greater than the yield stress experienced by the material in a uniaxial tensile test.
In terms of stress components Von Mises stress can be written as
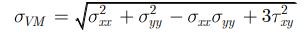
For 2D plane stress state σ3=0, the Von Mises stress in terms of principal stress can be expressed as follows
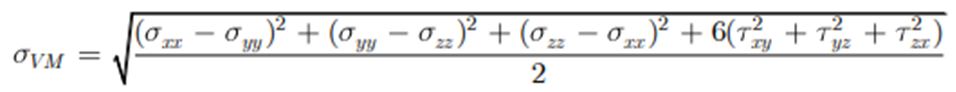

I am Sangeeta Das. I have completed my Masters in Mechanical Engineering with specialization in I.C Engine and Automobiles. I have around ten years of experience encompassing industry and academia. My area of interest includes I.C. Engines, Aerodynamics and Fluid Mechanics. You can reach me at