Comprehensive Guide to the Viscosity of Tar

by

Tar is a complex, viscous liquid derived from the distillation of organic materials, such as coal or petroleum. The viscosity of tar is a critical property that determines its flow behavior and plays a crucial role in various industrial applications, including road construction, roofing, and the production of carbon-based materials. This comprehensive guide delves into the intricacies of tar viscosity, providing a detailed exploration of the measurement techniques, temperature dependence, and theoretical explanations behind this important characteristic.

Viscosity-Temperature Relationship

The viscosity of tar exhibits a strong dependence on temperature, which can be described using various mathematical models. One widely accepted relationship is the double logarithmic viscosity-temperature relationship, which fits the results well for coal tar pitches and refined tars, except for hard pitches, which are insensitive and unreliable.

The viscosity of tar can also be represented by a power function trendline, expressed as the equation y = ax^b, where a and b are empirical constants. This power function trendline has been successfully used to describe the viscosity-temperature relationship of tar from the Athabasca tar sands.

Measurement Techniques

viscosity of tar

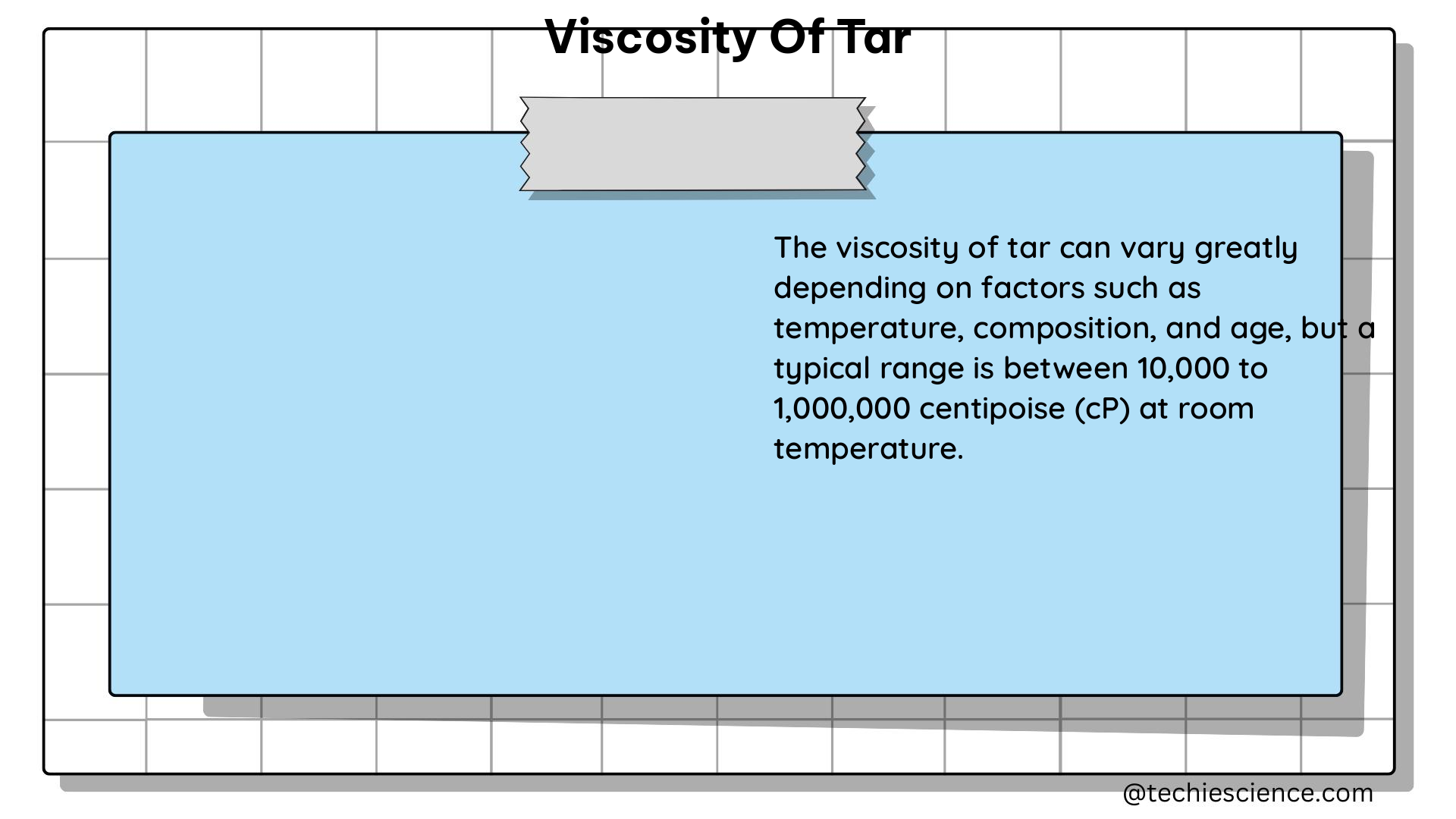
Researchers and industry professionals employ various techniques to measure the viscosity of tar, each with its own advantages and limitations. Two commonly used methods are:

  1. Capillary Viscometer: This method involves measuring the time it takes for a sample of tar to flow through a calibrated capillary tube. The viscosity is then calculated by multiplying the flow time with a predetermined calibration coefficient.

  2. Rotational Viscometer: This technique measures the resistance to flow on the surface of a rotating cylinder immersed in the tar sample. The viscosity is determined by adjusting the temperature and rotation speed according to the specific characteristics of the tar.

Viscosity Values

The viscosity of tar can be expressed in two forms: dynamic viscosity and kinematic viscosity.

  1. Dynamic Viscosity: The dynamic viscosity of tar is typically measured using a vacuum capillary viscometer. The procedure involves heating the sample, filling the viscometer, and recording the time it takes for the sample to flow through the viscometer.

  2. Kinematic Viscosity: The kinematic viscosity is the ratio of dynamic viscosity to density. It is measured using a capillary viscometer, and the procedure involves heating the sample, filling the viscometer, and recording the time it takes for the sample to flow through the viscometer.

Temperature Dependence

The viscosity of tar is highly sensitive to temperature changes. Measurements are typically conducted within a temperature range from room temperature to 135°C (275°F). As the temperature approaches the melting or freezing point of the tar, the viscosity increases significantly due to the formation of solid particles that impede free turbulence.

Examples and Data Points

Empirical data on the viscosity of tar can be found in various scientific publications and industry reports. For instance, Figure 6 in a reference paper shows viscosity data for molten iron and tar from the Athabasca tar sands, demonstrating how different fluids can be described by empirical curves.

Additionally, viscosity-temperature curves for various substances, including tar, provide valuable insights into how viscosity changes with temperature.

Theoretical Explanation

From a theoretical perspective, tar can be considered a Newtonian fluid, where the viscosity is simply the shearing stress divided by the shear rate. Empirical correlations, such as the power function trendline mentioned earlier, can be used to describe the viscosity-temperature relationship of tar.

Numerical Examples and Calculations

To illustrate the practical application of the concepts discussed, let’s consider a numerical example:

Suppose we have a sample of tar from the Athabasca tar sands, and we want to determine its viscosity at a temperature of 80°C. The power function trendline for the viscosity-temperature relationship of this tar is given by the equation:

η = 0.0012 × T^(-1.2)

where η is the dynamic viscosity in Pa·s and T is the temperature in Kelvin.

Substituting the given temperature of 80°C (353.15 K) into the equation, we get:

η = 0.0012 × 353.15^(-1.2) = 0.0012 × 0.2 = 0.00024 Pa·s

Therefore, the dynamic viscosity of the Athabasca tar sample at 80°C is approximately 0.00024 Pa·s.

Conclusion

The viscosity of tar is a complex and critical property that plays a significant role in various industrial applications. This comprehensive guide has explored the intricacies of tar viscosity, including the viscosity-temperature relationship, measurement techniques, viscosity values, temperature dependence, and theoretical explanations. By understanding the nuances of tar viscosity, researchers, engineers, and industry professionals can optimize processes, improve product quality, and enhance the performance of tar-based materials.

References

  1. https://www.sciencedirect.com/topics/materials-science/kinematic-viscosity
  2. https://www.researchgate.net/publication/230289804_Viscositytemperature_equations_for_coal_tar_pitches_and_refined_tars
  3. https://infinitygalaxy.org/viscosity-test-bitumen/
  4. https://en1.nbchao.com/k/10112/
  5. https://www.cedengineering.com/userfiles/All%20About%20Viscosity.pdf