The Initial Velocity Formula: A Comprehensive Guide for Physics Students

Summary

The initial velocity formula, a fundamental concept in physics, is a crucial tool for understanding and analyzing the motion of objects. This formula, derived from the equations of motion, allows us to calculate the initial velocity of an object given its final velocity, acceleration, and time or distance traveled. With its wide-ranging applications in fields such as physics, engineering, and sports science, mastering the initial velocity formula is essential for any physics student.

Understanding the Initial Velocity Formula

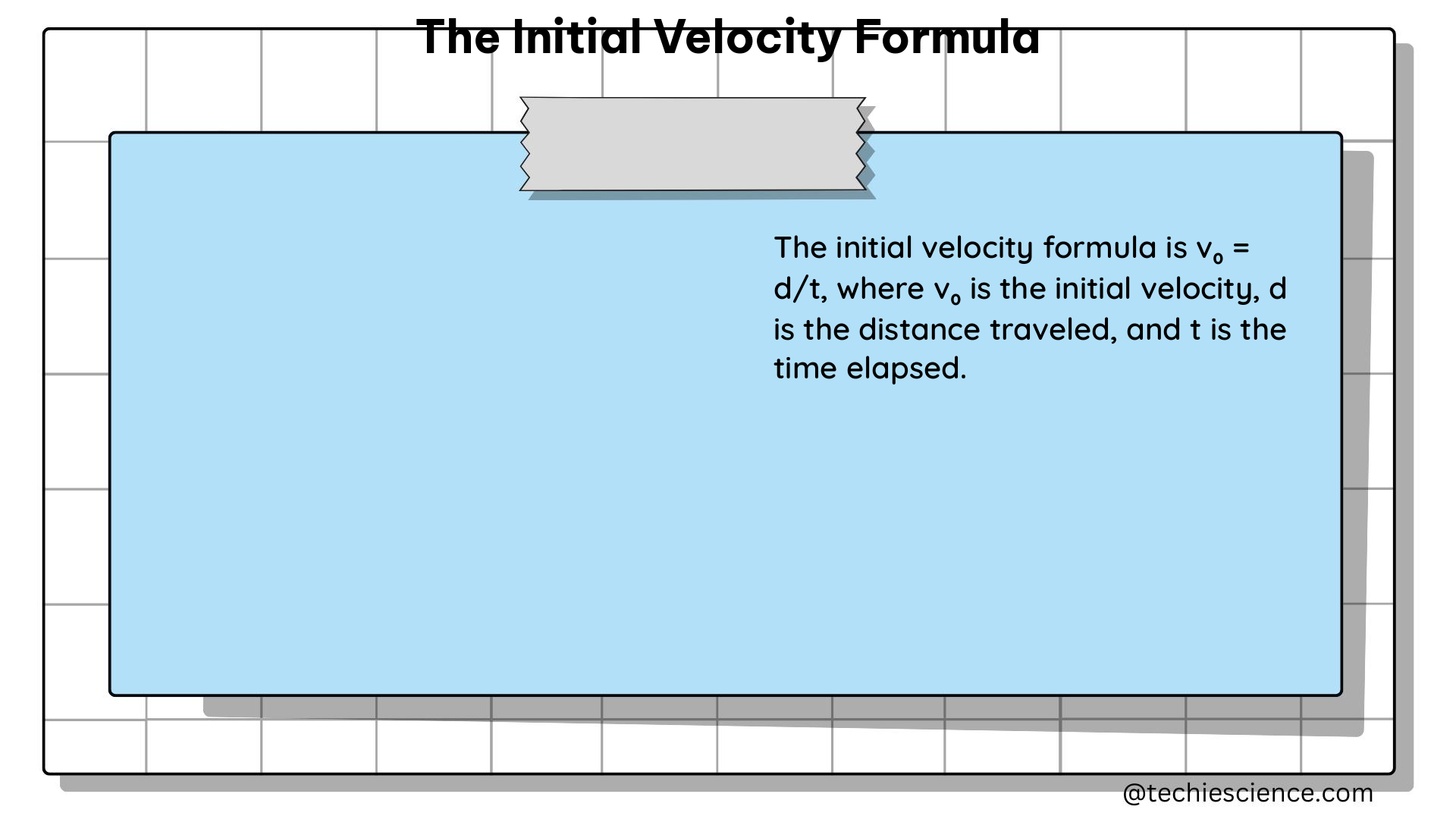
The initial velocity formula is expressed as:

u = v - at

Where:
– u is the initial velocity
– v is the final velocity
– a is the acceleration
– t is the time taken

This formula can be used to calculate the initial velocity of an object if the final velocity, acceleration, and time taken are known. Alternatively, if the final velocity, acceleration, and distance traveled are known, the formula can be rearranged to:

u^2 = v^2 - 2as

Where:
– u is the initial velocity
– v is the final velocity
– a is the acceleration
– s is the distance traveled

Derivation of the Initial Velocity Formula

The initial velocity formula is derived from the equations of motion, which describe the motion of an object over time. These equations are based on Newton’s laws of motion, which establish the relationship between force, mass, and acceleration.

The equations of motion are:

1. v = u + at
2. s = ut + 1/2 at^2
3. v^2 = u^2 + 2as

By rearranging these equations, we can derive the initial velocity formula:

1. From equation 1, we can isolate u:
   u = v - at

2. From equation 3, we can also derive the initial velocity formula:
   u^2 = v^2 - 2as

Applications of the Initial Velocity Formula

The initial velocity formula has numerous practical applications in various fields, including:

Physics

• Calculating the initial velocity of a ball thrown in the air
• Analyzing the motion of projectiles, such as a cannon ball or a baseball

Engineering

• Determining the initial velocity of a car moving down a ramp
• Designing and optimizing the launch systems of rockets and other aerospace vehicles

Sports Science

• Calculating the initial velocity of a baseball or tennis ball thrown by an athlete
• Analyzing the performance of athletes in sports that involve projectile motion, such as shot put, javelin throw, or long jump

Numerical Examples

1. Example 1: A ball is thrown upward with an initial velocity of 20 m/s. If the acceleration due to gravity is 9.8 m/s^2, what is the ball’s final velocity when it reaches its maximum height?

Given:
– Initial velocity (u) = 20 m/s
– Acceleration (a) = -9.8 m/s^2 (downward acceleration due to gravity)
– Time (t) = unknown

Using the initial velocity formula:
u = v - at
20 = v - (-9.8)t
v = 20 + 9.8t

At the maximum height, the final velocity (v) is 0 m/s.
Substituting v = 0 in the equation:
0 = 20 + 9.8t
t = 2.04 s

Therefore, the final velocity at the maximum height is 0 m/s.

1. Example 2: A car accelerates from rest (initial velocity of 0 m/s) to a final velocity of 20 m/s in 5 seconds. What is the car’s acceleration?

Given:
– Initial velocity (u) = 0 m/s
– Final velocity (v) = 20 m/s
– Time (t) = 5 s

Using the initial velocity formula:
u = v - at
0 = 20 - 5a
a = 4 m/s^2

Therefore, the car’s acceleration is 4 m/s^2.

1. Example 3: A projectile is launched with an initial velocity of 50 m/s at an angle of 60 degrees above the horizontal. If the acceleration due to gravity is 9.8 m/s^2, what is the maximum height reached by the projectile?

Given:
– Initial velocity (u) = 50 m/s
– Angle (θ) = 60 degrees
– Acceleration (a) = -9.8 m/s^2 (downward acceleration due to gravity)

Using the initial velocity formula and trigonometry:
u_x = u cos(θ) = 50 cos(60°) = 25 m/s
u_y = u sin(θ) = 50 sin(60°) = 43.3 m/s

The maximum height is reached when the vertical velocity (v_y) is 0 m/s.
v_y = u_y + at
0 = 43.3 - 9.8t
t = 4.42 s

Substituting the time in the vertical displacement equation:
s = u_yt + 1/2 at^2
s = 43.3 × 4.42 - 1/2 × 9.8 × 4.42^2
s = 191.4 - 95.7 = 95.7 m

Therefore, the maximum height reached by the projectile is 95.7 m.

Limitations and Assumptions

The initial velocity formula is based on the following assumptions:

1. Constant Acceleration: The formula assumes that the acceleration of the object remains constant throughout the motion.
2. Negligible Air Resistance: The formula does not consider the effects of air resistance or other external forces that may act on the object.
3. Uniform Motion: The formula is applicable for objects undergoing uniform motion, where the velocity changes linearly with time.

It’s important to note that in real-world scenarios, these assumptions may not always hold true, and other factors may need to be considered for more accurate calculations.

Conclusion

The initial velocity formula is a fundamental concept in physics that allows us to calculate the initial velocity of an object given its final velocity, acceleration, and time or distance traveled. This formula has a wide range of applications in various fields, including physics, engineering, and sports science. By understanding the derivation and limitations of the initial velocity formula, physics students can effectively apply it to solve a variety of problems and gain a deeper understanding of the principles of motion.

References

1. https://study.com/academy/lesson/parabolic-path-definition-projectiles-quiz.html
2. https://openoregon.pressbooks.pub/bodyphysics/chapter/quantitative-motion-analysis/
3. https://www.sciencedirect.com/topics/computer-science/initial-velocity
4. https://byjus.com/initial-velocity-formula/
5. https://study.com/skill/learn/how-to-calculate-the-range-of-a-projectile-explanation.html