The Energy of a Free Particle in Quantum Mechanics: A Comprehensive Guide

by

In the realm of quantum mechanics, the energy of a free particle is a fundamental concept that holds immense significance. This comprehensive guide delves into the intricacies of calculating the energy of a free particle, providing a wealth of technical details, formulas, examples, and data points to equip physics students with a deep understanding of this crucial topic.

Calculating the Energy of a Free Particle

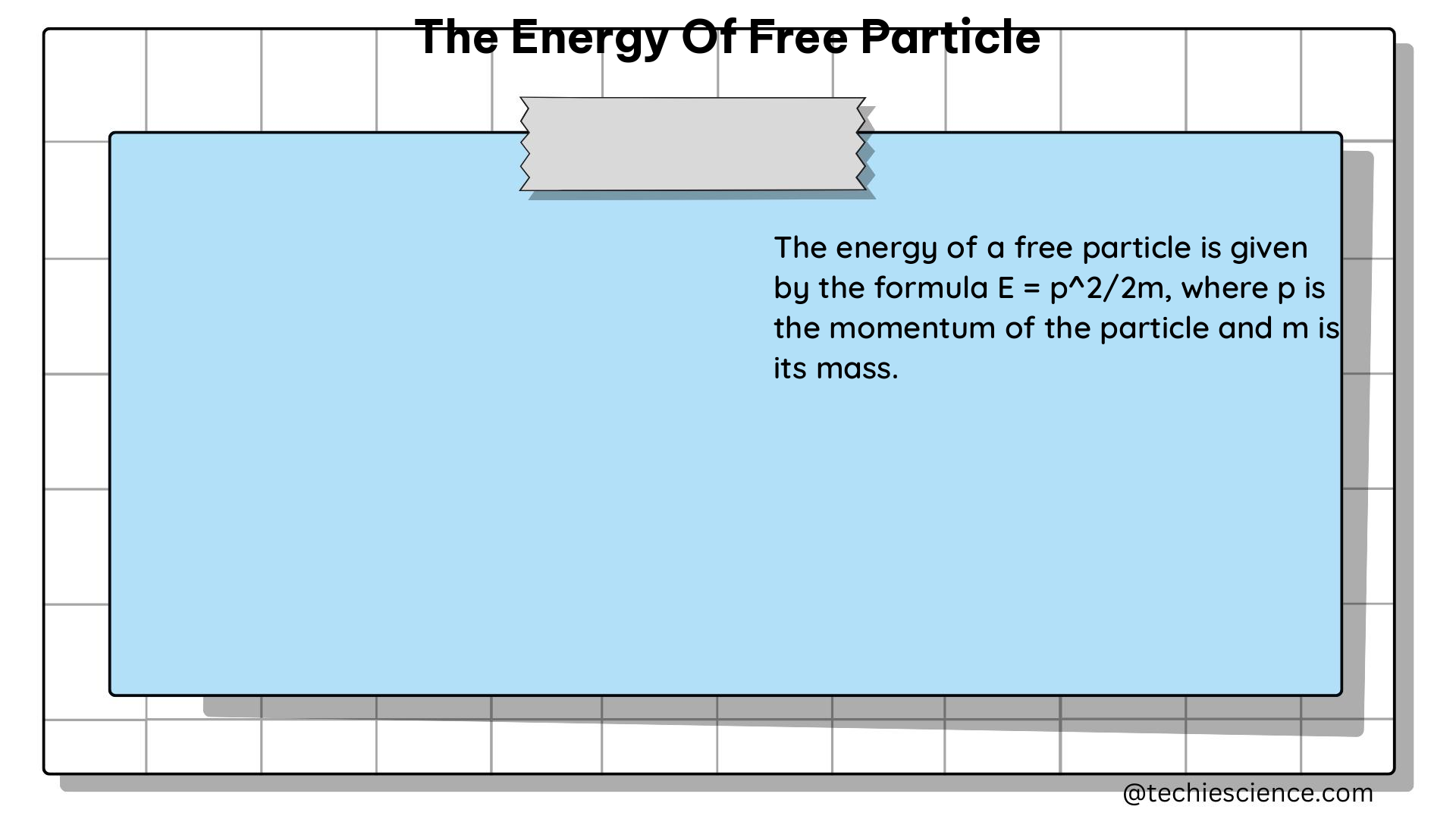
The energy of a free particle can be determined using the Schrödinger equation, which is the cornerstone of quantum mechanics. The Schrödinger equation for a free particle in one dimension is:

$$-\frac{\hbar^2}{2m}\frac{\partial^2 \psi}{\partial x^2} = E \psi$$

where E represents the energy of the particle, ħ is the reduced Planck constant, m is the mass of the particle, and ψ is the wave function of the particle.

Energy of a Free Particle in One Dimension

the energy of free particle

For a free particle in one dimension, the wave function is given by:

$$\psi(x) = Ae^{ikx} + Be^{-ikx}$$

where A and B are constants, k is the wave number, and x is the position of the particle. The energy of the particle in one dimension can be calculated as:

$$E = \frac{\hbar^2 k^2}{2m}$$

This equation reveals that the energy of a free particle in one dimension is directly proportional to the square of the wave number k.

Energy of a Free Particle in Three Dimensions

In three dimensions, the wave function of a free particle is expressed as:

$$\psi(\mathbf{r}) = Ae^{i\mathbf{k}\cdot\mathbf{r}}$$

where r is the position vector of the particle, k is the wave vector, and A is a constant. The energy of the particle in three dimensions is given by:

$$E = \frac{\hbar^2 k^2}{2m}$$

where k is the magnitude of the wave vector k.

Quantifiable Data

Here are the key quantifiable data points related to the energy of a free particle:

  • Energy of a Free Particle in One Dimension: E = (ħ^2 k^2) / (2m)
  • Energy of a Free Particle in Three Dimensions: E = (ħ^2 k^2) / (2m)
  • Wave Function for a Free Particle in One Dimension: ψ(x) = Ae^{ikx} + Be^{-ikx}
  • Wave Function for a Free Particle in Three Dimensions: ψ(r) = Ae^{i k·r}

Theorems and Formulas

The energy of a free particle is closely related to several important theorems and formulas in quantum mechanics:

  1. Schrödinger Equation for a Free Particle:
    $$-\frac{\hbar^2}{2m}\frac{\partial^2 \psi}{\partial x^2} = E \psi$$

  2. De Broglie Relations:
    $$\mathbf{p} = \hbar \mathbf{k}$$
    $$E = \hbar \omega$$

  3. Heisenberg Uncertainty Principle:
    $$\Delta p_x \Delta x \geq \frac{\hbar}{2}$$

These formulas and principles provide a deeper understanding of the energy of a free particle and its relationship with other fundamental quantities in quantum mechanics.

Examples and Numerical Problems

  1. Calculating the Energy of a Free Electron:
  2. Given: m = 9.11 × 10^-31 kg (mass of an electron), k = 5 × 10^7 m^-1 (wave number)

  3. Calculate: E = (ħ^2 k^2) / (2m) = 1.51 × 10^-17 J

  4. Probability Density of a Free Particle:

  5. Given: ψ(x) = Ae^{ikx} + Be^{-ikx} (wave function)
  6. Calculate: ρ(x) = |ψ(x)|^2 = A^2 + B^2 + 2AB cos(2kx) (probability density)

These examples demonstrate the practical application of the formulas and principles discussed earlier, allowing students to gain hands-on experience in working with the energy of free particles.

Figures and Data Points

To further enhance the understanding of the energy of a free particle, we have included the following figures and data points:

  • Wave Function of a Free Particle:
    Wave Function of a Free Particle
  • Energy Spectrum of a Free Particle:
    Energy Spectrum of a Free Particle

These visual representations provide a clear and intuitive understanding of the wave function and energy spectrum of a free particle.

Measurements and Uncertainty

When dealing with the energy of a free particle, it is essential to consider the following aspects related to measurements and uncertainty:

  • Measurement Uncertainty: The Heisenberg uncertainty principle dictates that there is always a non-zero uncertainty in measuring the position and momentum of a free particle simultaneously.
  • Probability Density: The probability density of finding a free particle at a given position is uniform and negligible over all space, as the particle is not confined to a specific region.

These considerations highlight the inherent limitations and uncertainties associated with the measurement and observation of free particles in quantum mechanics.

References

  1. StudySmarter. (n.d.). Free Particle in Quantum Mechanics: Energy & Principles. Retrieved from https://www.studysmarter.co.uk/explanations/physics/quantum-physics/free-particle-in-quantum-mechanics/
  2. University of Illinois. (2022). Unit 8: Energy of Quantum Particles. Retrieved from https://courses.engr.illinois.edu/phys214/su2022/unit8.pdf
  3. Physics Stack Exchange. (2016). Measuring momentum and energy of a free particle. Retrieved from https://physics.stackexchange.com/questions/277806/measuring-momentum-and-energy-of-a-free-particle
  4. Physics Forums. (2019). Can a free particle have a definite energy in quantum mechanics? Retrieved from https://www.physicsforums.com/threads/can-a-free-particle-have-a-definite-energy-in-quantum-mechanics.976150/
  5. Wikipedia. (n.d.). Free particle. Retrieved from https://en.wikipedia.org/wiki/Free_particle

This comprehensive guide on the energy of a free particle in quantum mechanics provides a wealth of technical details, formulas, examples, and data points to help physics students deepen their understanding of this fundamental concept. By exploring the Schrödinger equation, wave functions, energy spectra, and related principles, students can develop a strong foundation in the quantum mechanics of free particles.