The telescope magnification formula is a fundamental concept in astronomy that allows astronomers and amateur stargazers to determine the magnification power of a telescope. This formula is crucial for understanding the capabilities and limitations of a telescope, enabling users to choose the right equipment for their observational needs. In this comprehensive guide, we will delve into the intricacies of the telescope magnification formula, providing a detailed exploration of its components, applications, and practical examples.
The Telescope Magnification Formula
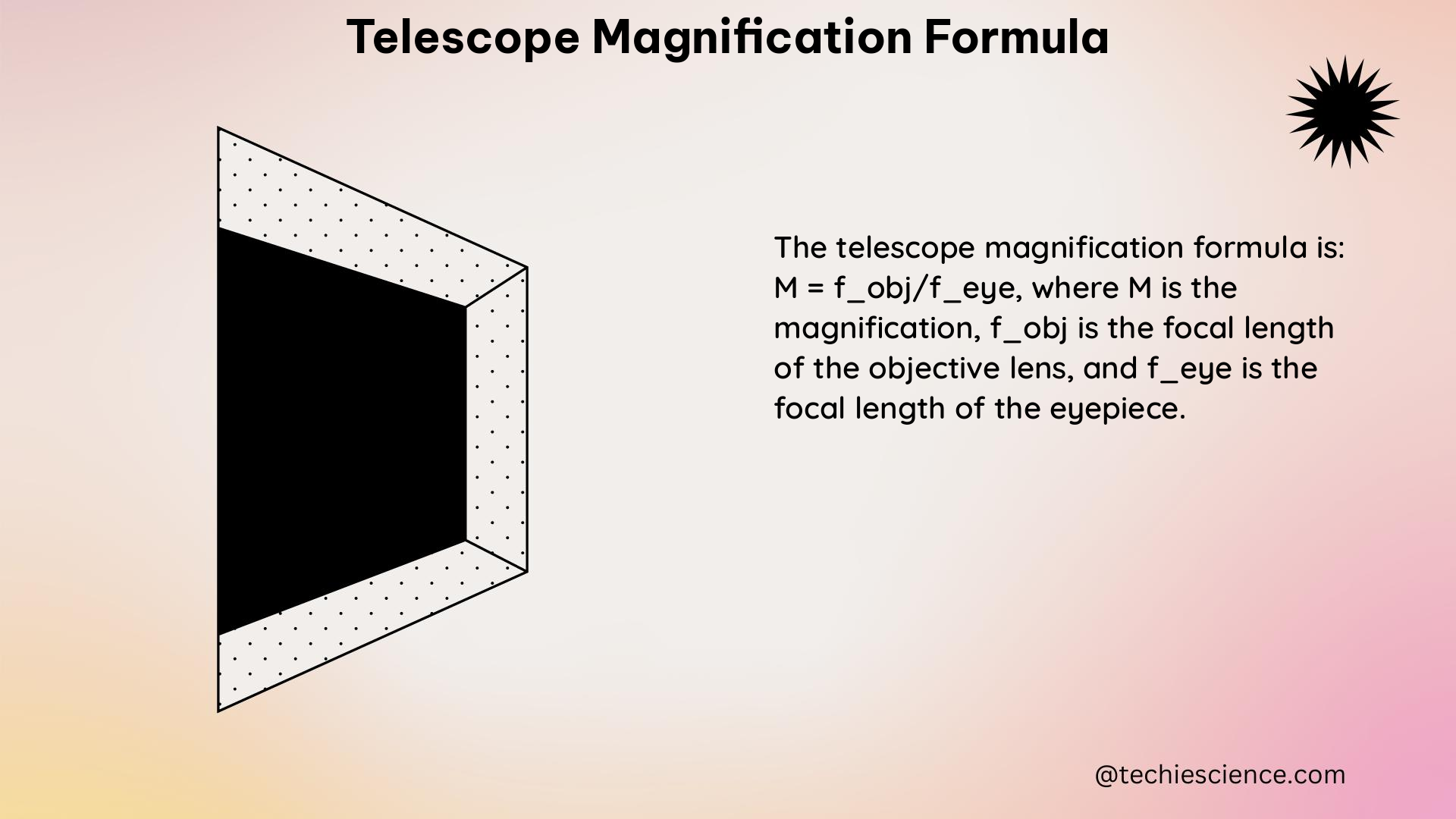
The magnification of a telescope is calculated using the following formula:
[ M = \frac{f_t}{f_e} ]
where:
– ( M ) is the magnification
– ( f_t ) is the focal length of the telescope
– ( f_e ) is the focal length of the eyepiece
This formula demonstrates that the magnification of a telescope is directly proportional to the ratio of the telescope’s focal length to the eyepiece’s focal length. By adjusting the eyepiece, astronomers can achieve different levels of magnification to suit their observational requirements.
Minimum Magnification
The minimum useful magnification of a telescope is limited by its aperture, which is the diameter of the primary lens or mirror. The minimum magnification is calculated as:
[ M_{min} = \frac{\text{aperture in mm}}{7} ]
This formula suggests that a telescope with a larger aperture can achieve a higher minimum magnification. For example, a telescope with a 200 mm lens aperture has a minimum useful magnification of around 28 times.
Optimum Magnification
The optimum magnification, also known as the maximum useful magnification, is the point at which a star no longer appears as a point-like source but rather as a tiny disk with diffraction rings. This magnification is calculated as:
[ M_{opt} = \frac{\text{aperture in mm}}{0.7} ]
For instance, a telescope with an aperture of 100 mm has an optimum magnification of 142 times, while a 200 mm telescope has an optimum magnification of 285 times.
Maximum Magnification
Each telescope has a magnification limit, which is equivalent to 2 times the lens aperture. This maximum magnification is calculated as:
[ M_{max} = 2 \times \text{aperture in mm} ]
For a telescope with a 200 mm lens aperture, the maximum magnification would be 400 times.
Angular Magnification
Angular magnification is the apparent size of an object when viewed through a telescope, compared to the angle subtended by the object when viewed with the naked eye. This concept is crucial for understanding the visual impact of different magnification levels.
Examples and Data
To illustrate the application of the telescope magnification formula, let’s consider some specific telescope models and their corresponding magnification values:
| Telescope Model | Aperture | Focal Length | Eyepiece Focal Length | Magnification |
|---|---|---|---|---|
| 8-inch Orion Reflector | 203 mm | 1198 mm | 10 mm | 120x |
| Obsession-20 Reflector | 508 mm | 2540 mm | 8 mm | 317x |
| Hubble Reflector | 2400 mm | 57600 mm | 20 mm | 2880x |
These examples demonstrate the wide range of magnification capabilities that can be achieved with different telescope designs and configurations.
Practical Considerations
When using the telescope magnification formula, it’s important to consider the following practical factors:
- Atmospheric Conditions: The Earth’s atmosphere can introduce turbulence and distortion, limiting the maximum useful magnification.
- Eyepiece Quality: The quality and design of the eyepiece can affect the overall image quality and perceived magnification.
- Observational Conditions: Factors such as light pollution, sky transparency, and the observer’s visual acuity can influence the optimal magnification.
By understanding these practical considerations, astronomers can make informed decisions about the appropriate magnification for their observational needs and the specific telescope they are using.
Conclusion
The telescope magnification formula is a fundamental tool for understanding and optimizing the performance of telescopes. By mastering this formula and its associated concepts, astronomers and amateur stargazers can make informed choices about their equipment, ensuring they can observe celestial objects with the desired level of detail and clarity. This comprehensive guide has provided a detailed exploration of the telescope magnification formula, equipping you with the knowledge and understanding to make the most of your astronomical observations.
References
- Sky and Telescope – “How to Choose Your Telescope Magnification” (https://skyandtelescope.org/astronomy-equipment/choosing-your-telescopes-magnification/)
- RocketMime – “Telescope Equations: Magnification” (https://www.rocketmime.com/astronomy/Telescope/Magnification.html)
- Space Math @ NASA – “Calculating the Magnification of a Telescope” (https://spacemath.gsfc.nasa.gov/weekly/10Page32.pdf)
- Astroshop.eu – “Magnification” (https://www.astroshop.eu/magazine/information/telescope-information/the-right-telescope/magnification/i,1063)
- Mr Toogood Physics – “Telescopes and their limitations” (http://www.alevelphysicsnotes.com/astrophysics/telescopes.php)

The lambdageeks.com Core SME Team is a group of experienced subject matter experts from diverse scientific and technical fields including Physics, Chemistry, Technology,Electronics & Electrical Engineering, Automotive, Mechanical Engineering. Our team collaborates to create high-quality, well-researched articles on a wide range of science and technology topics for the lambdageeks.com website.
All Our Senior SME are having more than 7 Years of experience in the respective fields . They are either Working Industry Professionals or assocaited With different Universities. Refer Our Authors Page to get to know About our Core SMEs.