Mastering Telescope Airy Disc Calculations: A Comprehensive Guide

The Airy disc is a fundamental concept in telescope optics, representing the smallest point to which a beam of light can be focused. Understanding the Airy disc and its associated calculations is crucial for determining the resolving power and performance of a telescope. In this comprehensive guide, we will delve into the intricacies of Airy disc calculations, providing you with the necessary tools and knowledge to become an expert in this field.

Understanding the Airy Disc

The Airy disc is the diffraction pattern created by a circular aperture, such as the objective lens or mirror of a telescope. This pattern is characterized by a central bright spot surrounded by concentric bright and dark rings. The diameter of the Airy disc is a crucial parameter in determining the telescope’s resolving power, as it represents the smallest point to which a beam of light can be focused.

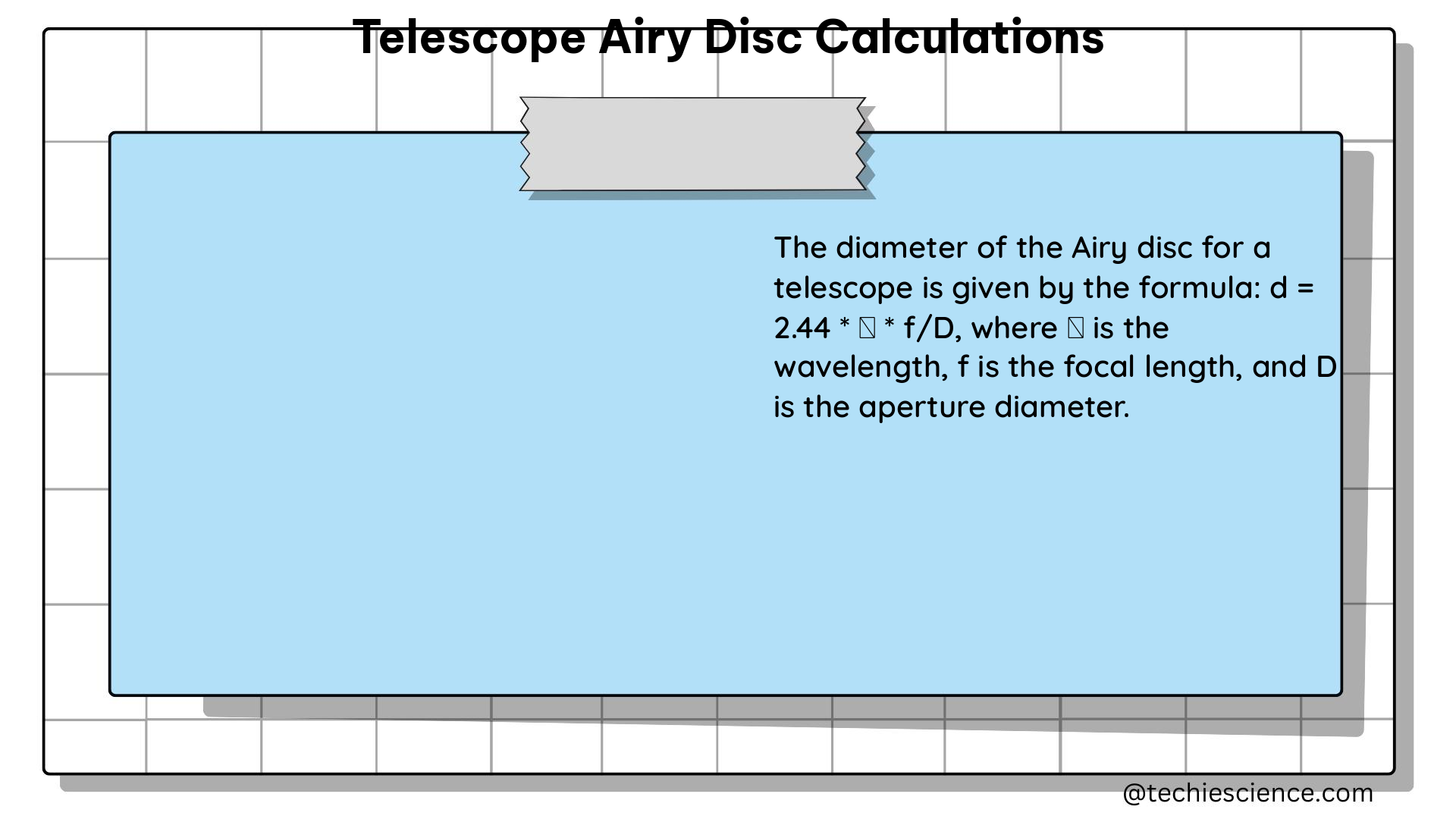
The formula for calculating the Airy disc diameter is:

∆θ = 2.44λ/D

Where:
– ∆θ is the angular resolution in radians
– λ is the wavelength of light
– D is the diameter of the telescope’s objective

This formula can be used to calculate the Airy disc diameter for a given telescope and wavelength of light.

Factors Affecting Airy Disc Size

The size of the Airy disc is influenced by several factors, including:

1. Telescope Aperture (D): The larger the telescope’s aperture, the smaller the Airy disc diameter. This is because a larger aperture can focus light more effectively, resulting in a tighter diffraction pattern.

2. Wavelength of Light (λ): The Airy disc diameter is inversely proportional to the wavelength of light. Shorter wavelengths, such as blue light, will have a smaller Airy disc compared to longer wavelengths, such as red light.

3. Optical Aberrations: Imperfections in the telescope’s optics, such as spherical aberration, coma, or astigmatism, can distort the Airy disc and increase its apparent size.

4. Atmospheric Turbulence (Seeing): The Earth’s atmosphere can cause distortions in the light path, leading to a larger Airy disc and reduced image quality. This effect is known as atmospheric seeing.

5. Guiding Errors: Inaccuracies in the telescope’s tracking system can cause the image to drift, resulting in a larger Airy disc and reduced image quality.

Understanding these factors is crucial when evaluating the performance of a telescope and predicting the achievable resolution.

Airy Disc Calculations: Examples and Numerical Problems

Let’s explore some examples and numerical problems to illustrate the application of Airy disc calculations.

Example 1:
Suppose you have a 25-inch (635 mm) f/3.0 telescope. Calculate the Airy disc diameter for green light (550 nm).

Given:
– Telescope Aperture (D) = 635 mm
– Wavelength of Light (λ) = 550 nm

Using the formula:
∆θ = 2.44λ/D
∆θ = 2.44 × 550 × 10^-9 m / 635 × 10^-3 m
∆θ = 2.12 × 10^-6 radians

Converting to arcseconds:
∆θ = 2.12 × 10^-6 radians × (206,265 arcseconds/radian)
∆θ = 0.44 arcseconds

Therefore, the Airy disc diameter for this telescope and wavelength is approximately 0.44 arcseconds.

Numerical Problem 1:
A telescope has an aperture of 12 inches (304.8 mm). Calculate the Airy disc diameter for the following wavelengths:
– Red light (650 nm)
– Green light (550 nm)
– Blue light (450 nm)

Solution:
Using the formula: ∆θ = 2.44λ/D

For red light (650 nm):
∆θ = 2.44 × 650 × 10^-9 m / 304.8 × 10^-3 m
∆θ = 5.24 × 10^-6 radians
∆θ = 1.08 arcseconds

For green light (550 nm):
∆θ = 2.44 × 550 × 10^-9 m / 304.8 × 10^-3 m
∆θ = 4.43 × 10^-6 radians
∆θ = 0.91 arcseconds

For blue light (450 nm):
∆θ = 2.44 × 450 × 10^-9 m / 304.8 × 10^-3 m
∆θ = 3.63 × 10^-6 radians
∆θ = 0.75 arcseconds

Therefore, the Airy disc diameters for the given wavelengths are:
– Red light (650 nm): 1.08 arcseconds
– Green light (550 nm): 0.91 arcseconds
– Blue light (450 nm): 0.75 arcseconds

Resolving Power and Empirical Criteria

The Airy disc diameter is not the only factor that determines a telescope’s resolving power. Two other important empirical criteria are the Dawes limit and the Rayleigh limit.

Dawes Limit

The Dawes limit is an empirical criterion used to estimate the minimum separation at which a double star can be resolved by the human eye. The formula for the Dawes limit is:

∆θ = 116/D

Where:
– ∆θ is the angular separation in arcseconds
– D is the diameter of the telescope’s objective in millimeters

This formula can be used to estimate the minimum separation at which a double star can be resolved by a given telescope.

Rayleigh Limit

The Rayleigh limit is another empirical criterion used to estimate the minimum separation at which two points can be resolved by an optical system. The formula for the Rayleigh limit is:

∆θ = 1.22λ/D

Where:
– ∆θ is the angular resolution in radians
– λ is the wavelength of light
– D is the diameter of the telescope’s objective

This formula can be used to estimate the minimum separation at which two points can be resolved by a given telescope.

It’s important to note that the Dawes limit and Rayleigh limit are empirical criteria and may not always accurately predict the actual resolving power of a telescope, as they do not account for factors such as atmospheric seeing, guiding errors, and other aberrations.

Practical Considerations and Limitations

In practice, the actual full-width at half-maximum (FWHM) achieved with typical CCD systems and mounts can be significantly larger than the theoretical Airy disc diameter, particularly for larger aperture telescopes. This is due to various factors, including:

1. Atmospheric Seeing: The turbulence in the Earth’s atmosphere can cause distortions in the light path, leading to a larger FWHM and reduced image quality.

2. Guiding Errors: Inaccuracies in the telescope’s tracking system can cause the image to drift, resulting in a larger FWHM and reduced image quality.

3. Optical Aberrations: Imperfections in the telescope’s optics, such as spherical aberration, coma, or astigmatism, can distort the Airy disc and increase its apparent size.

4. Sensor Pixel Size: The size of the pixels in the camera’s sensor can also affect the measured FWHM, as the sensor may not be able to fully sample the Airy disc.

These practical limitations should be considered when evaluating the performance of a telescope and interpreting the results of Airy disc calculations.

Conclusion

The Airy disc is a fundamental concept in telescope optics, and understanding its calculations is crucial for determining the resolving power and performance of a telescope. In this comprehensive guide, we have explored the formula for calculating the Airy disc diameter, the factors that affect its size, and the application of Airy disc calculations through examples and numerical problems.

Additionally, we have discussed the Dawes limit and Rayleigh limit, which are empirical criteria used to estimate the minimum separation at which a double star or two points can be resolved by a given telescope. Finally, we have highlighted the practical considerations and limitations that can affect the actual FWHM achieved in practice, emphasizing the importance of considering these factors when evaluating the performance of a telescope.

By mastering the concepts and techniques presented in this guide, you will be well-equipped to tackle telescope Airy disc calculations and optimize the performance of your telescope for your observational needs.

References

1. Airy Disc Calculator: https://www.edmundoptics.com/knowledge-center/application-notes/imaging/limitations-on-resolution-and-contrast-the-airy-disk/
2. Dawes Limit Calculator: https://www.aatastro.org/resources/dawes-limit-calculator/
3. Rayleigh Limit Calculator: https://www.aatastro.org/resources/rayleigh-limit-calculator/
4. FWHM Expectations for Larger Aperture Instruments: https://www.aavso.org/fwhm-expectations-larger-aperture-instruments
5. Comparison of the Calculation of the Airy Disk Phase Using Analytical and Numerical Methods: https://www.researchgate.net/figure/Comparison-of-the-calculation-of-the-Airy-disk-phase-using-analytical-and-numerical_fig3_347125733
6. Napier-Munn, R. J. (2014). The Dawes Limit and the Rayleigh Criterion. Journal of Double Star Observations, 4(4), 201-205. http://www.jdso.org/volume4/number4/Napier_Munn.pdf