Tangential Acceleration Formula: A Comprehensive Guide

Tangential acceleration is a crucial concept in the study of rotational motion and dynamics. It represents the rate at which the tangential velocity of an object changes during its circular motion. The formula for tangential acceleration is a fundamental tool for understanding and analyzing the behavior of rotating systems.

Understanding Tangential Acceleration

Tangential acceleration, denoted as at, is the acceleration that acts in the direction of the tangent to the circular path of an object. It is distinct from radial acceleration, which is the acceleration directed towards the center of the circular path. Tangential acceleration is responsible for changes in the speed of the object, while radial acceleration is responsible for changes in the direction of the velocity.

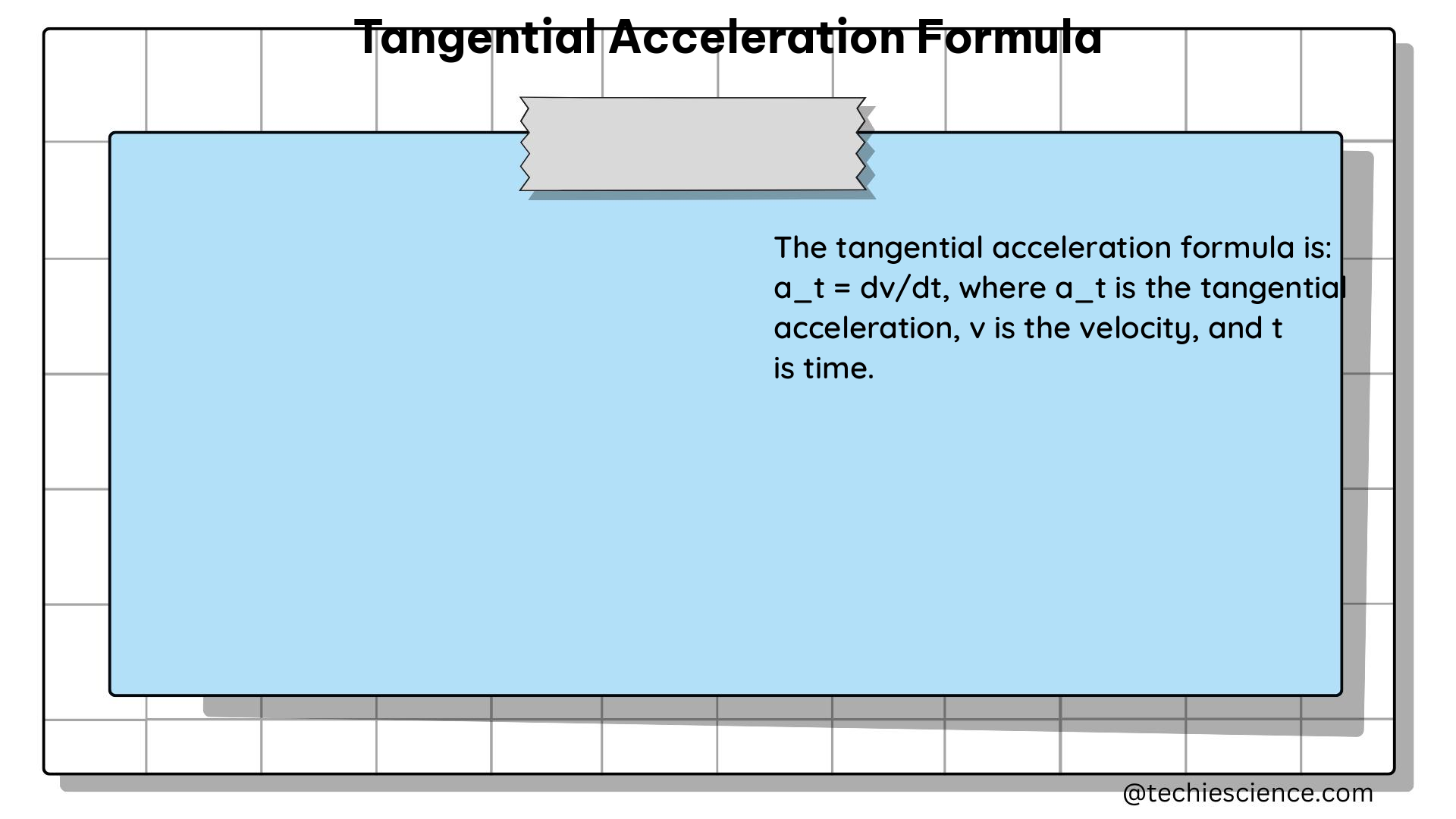
The formula for tangential acceleration is given by:

at = r × α

Where:
– at is the tangential acceleration (in m/s²)
– r is the radius of the circular path (in m)
– α is the angular acceleration of the object (in rad/s²)

This formula can also be expressed in terms of angular velocity (ω) and time (t):

at = r × (ω/t)

Where:
– ω is the angular velocity of the object (in rad/s)
– t is the time taken (in s)

Additionally, the formula can be written in terms of angular displacement (θ) and time (t):

at = r × (θ/t²)

Where:
– θ is the angular displacement or angle of rotation (in rad)
– t is the time taken (in s)

Tangential Acceleration in Uniform Circular Motion

In the case of uniform circular motion, where the angular velocity remains constant, the tangential acceleration is zero. This is because the speed of the object does not change, and the only acceleration present is the radial (centripetal) acceleration, which is responsible for the change in the direction of the velocity.

The formula for tangential acceleration in uniform circular motion is:

at = 0

Tangential Acceleration Examples

1. Example 1: An object is undergoing circular motion with a radius of 5 meters and an angular acceleration of 2 rad/s².

2. Tangential acceleration: at = r × α = 5 × 2 = 10 m/s²

3. Example 2: An object is undergoing circular motion with a radius of 12 meters and an angular acceleration of 0.5 rad/s².

4. Tangential acceleration: at = r × α = 12 × 0.5 = 6 m/s²

5. Example 3: An object is undergoing circular motion with an angular velocity of 10 rad/s and the motion takes 5 seconds to complete.

6. Tangential acceleration: at = r × (ω/t) = r × (10/5) = 2r m/s²

7. Example 4: An object is undergoing circular motion with an angular displacement of 30 radians and the motion takes 5 seconds to complete.

8. Tangential acceleration: at = r × (θ/t²) = r × (30/25) = 1.2r m/s²

Tangential Acceleration in Real-World Applications

Tangential acceleration is an important concept in various fields, including:

1. Rotational Machinery: In the design and analysis of rotating machinery, such as motors, turbines, and gears, understanding tangential acceleration is crucial for ensuring proper operation, efficiency, and safety.

2. Automotive Engineering: In the study of vehicle dynamics, tangential acceleration plays a role in analyzing the performance and handling characteristics of vehicles during cornering and acceleration.

3. Robotics and Automation: Robotic systems that involve rotational motion, such as robotic arms and manipulators, rely on the understanding of tangential acceleration for precise control and coordination.

4. Sports and Athletics: Tangential acceleration is relevant in the analysis of sports involving rotational motion, such as discus throwing, hammer throwing, and certain gymnastics events.

5. Aerospace Engineering: In the design and analysis of aircraft and spacecraft, tangential acceleration is considered in the study of rotational motion, such as the motion of propellers, turbines, and control surfaces.

Tangential Acceleration Formulas and Theorems

1. Tangential Acceleration Formula:
2. at = r × α
3. at = r × (ω/t)

4. at = r × (θ/t²)

5. Theorem 1: In uniform circular motion, the tangential acceleration is zero.

6. at = 0

7. Theorem 2: The tangential acceleration is responsible for changes in the speed of the object, while the radial (centripetal) acceleration is responsible for changes in the direction of the velocity.

8. Theorem 3: The SI unit of tangential acceleration is m/s².

9. Theorem 4: Tangential acceleration is a vector quantity, meaning it has both magnitude and direction.

10. Theorem 5: Tangential acceleration is an important concept in the study of rotational motion and dynamics, particularly in the fields of physics, engineering, and applied sciences.

Tangential Acceleration Numerical Problems

1. Problem 1: An object is undergoing circular motion with a radius of 8 meters and an angular acceleration of 3 rad/s². Calculate the tangential acceleration of the object.

2. Solution: at = r × α = 8 × 3 = 24 m/s²

3. Problem 2: An object is undergoing circular motion with a radius of 6 meters and an angular velocity of 20 rad/s. The motion takes 4 seconds to complete. Calculate the tangential acceleration of the object.

4. Solution: at = r × (ω/t) = 6 × (20/4) = 30 m/s²

5. Problem 3: An object is undergoing circular motion with an angular displacement of 45 radians. The motion takes 3 seconds to complete. Calculate the tangential acceleration of the object.

6. Solution: at = r × (θ/t²) = r × (45/9) = 5r m/s²

7. Problem 4: A car is negotiating a circular turn with a radius of 50 meters. The car’s angular velocity increases from 10 rad/s to 20 rad/s in 2 seconds. Calculate the tangential acceleration of the car.

8. Solution: at = r × (Δω/Δt) = 50 × (10/2) = 250 m/s²

9. Problem 5: A rotating shaft has a radius of 0.2 meters and an angular acceleration of 4 rad/s². Calculate the tangential acceleration of a point on the shaft that is 0.2 meters from the center.

10. Solution: at = r × α = 0.2 × 4 = 0.8 m/s²

These examples demonstrate the application of the tangential acceleration formula in various scenarios, covering different parameters such as radius, angular acceleration, angular velocity, and angular displacement.

Conclusion

The tangential acceleration formula is a fundamental tool in the study of rotational motion and dynamics. By understanding the relationship between the radius, angular acceleration, angular velocity, and angular displacement, you can effectively analyze and solve problems involving the changes in the speed of rotating objects. This knowledge is crucial in various fields, including engineering, physics, and applied sciences, where the analysis of rotational motion is essential.

References

1. How to Calculate the Tangential Acceleration of an Object Moving in a Circle – Explanation
2. Tangential Acceleration Formula
3. Tangential & Normal Components of Circular Motion
4. Rotational Motion and Dynamics
5. Circular Motion and Centripetal Force