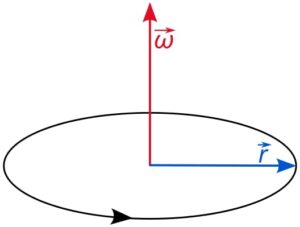
The concept of RPM (revolutions per minute) and angular velocity is essential in understanding the rotational motion of objects. RPM refers to the number of complete revolutions an object makes in one minute, while angular velocity measures the rate at which an object rotates in radians per second. To convert RPM to angular velocity, we need to multiply the RPM by 2π/60 to obtain the angular velocity in radians per second. This conversion factor accounts for the fact that there are 2π radians in one complete revolution and 60 seconds in one minute.
Key Takeaways
| RPM | Angular Velocity (rad/s) |
|---|---|
| 100 | 10.47 |
| 200 | 20.94 |
| 300 | 31.41 |
| 400 | 41.88 |
| 500 | 52.35 |
Understanding Angular Velocity
Angular velocity is a fundamental concept in physics that helps us understand the rotational motion of objects. It describes how fast an object is rotating or spinning around a fixed axis. In this article, we will explore the definition and concept of angular velocity, its relationship with rotational motion, and the unit of measurement used to quantify it.
Definition and Concept of Angular Velocity
Angular velocity is defined as the rate of change of angular displacement with respect to time. It measures how quickly an object is rotating or spinning. Just like linear velocity measures how fast an object is moving in a straight line, angular velocity measures how fast an object is rotating around an axis.
To better understand angular velocity, let’s consider a wheel rotating. As the wheel spins, different points on its rim move at different speeds. The angular velocity tells us how fast each point is moving in terms of the angle covered per unit of time. It is commonly denoted by the Greek letter omega (ω).
Relationship between Angular Velocity and Rotational Motion
Angular velocity is closely related to rotational motion. It helps us analyze and describe various aspects of objects in circular or rotational motion. By understanding angular velocity, we can determine the rotational speed, revolutions per minute (RPM), and angular speed of an object.
The relationship between angular velocity and linear velocity is also significant. Linear velocity is the speed of an object moving along a straight line, while angular velocity is the speed of an object rotating around an axis. The two are related through the concept of radius. The linear velocity of a point on a rotating object is equal to the product of its angular velocity and the distance from the axis of rotation.
Angular Velocity Unit: Radian per Second
Angular velocity is typically measured in radians per second (rad/s). Radians are a unit of measurement for angles, and they are particularly useful when dealing with circular motion. One radian is equal to the angle subtended at the center of a circle by an arc that is equal in length to the radius of the circle.
To convert angular velocity from degrees per second to radians per second, we can use the conversion factor of π/180. This conversion factor accounts for the fact that there are 2π radians in a complete circle and 360 degrees in a circle.
In summary, understanding angular velocity is crucial for comprehending rotational motion in physics. It allows us to analyze the speed and motion of rotating objects, and it is measured in radians per second. By exploring the relationship between angular velocity and rotational motion, we can gain insights into the dynamics of circular motion and solve various motion equations in rotational kinematics.
Converting RPM to Angular Velocity
Explanation of the Conversion Process
When it comes to rotational motion, one of the key parameters we often encounter is the rotational speed, commonly measured in revolutions per minute (RPM). However, in many cases, it is more convenient to work with angular velocity, which is measured in radians per second (rad/s). Converting RPM to angular velocity allows us to express rotational motion in a more universal and precise manner.
To understand the conversion process, we first need to establish the relationship between revolutions and radians. In circular motion, one revolution corresponds to a complete 360-degree rotation. Since there are 2π radians in a full circle, we can say that one revolution is equal to 2π radians.
Relationship between Revolutions and Radians
- One revolution = 2π radians
- Half a revolution = π radians
- Quarter of a revolution = π/2 radians
Now that we know the relationship between revolutions and radians, we can derive the conversion formula.
Conversion Formula: 1rpm = 2π/60 rad.s^-1
To convert RPM to angular velocity, we use the conversion factor of 2π/60 rad/s. This factor accounts for the fact that there are 60 seconds in a minute and 2π radians in one revolution.
To apply the conversion formula, we simply multiply the given RPM value by the conversion factor. The resulting value will be the angular velocity in rad/s.
Example: Converting 80 RPM to Angular Velocity
Let’s take an example to illustrate the conversion process. Suppose we have a wheel rotating at a speed of 80 RPM. To find the corresponding angular velocity, we can use the conversion formula:
Angular velocity = 80 RPM * (2π/60 rad/s)
Simplifying the equation, we get:
Angular velocity = 80 * 2π/60 rad/s
Calculating the value, we find that the angular velocity is approximately 8.377 rad/s.
By converting RPM to angular velocity, we can better understand and analyze rotational motion in terms of radians per second. This conversion allows us to apply the principles of physics and kinematics to solve problems related to rotational motion, such as determining rotational velocity, linear velocity, tangential velocity, and motion equations in rotational kinematics.
Remember, the conversion formula of 1rpm = 2π/60 rad/s is a useful tool when dealing with circular velocity, wheel rotation, spin rate, or any other scenario involving rotational speed.
Tools for Conversion
RPM to Angular Velocity Converter
When it comes to understanding rotational motion and circular velocity, one of the key concepts to grasp is the conversion between RPM (rotations per minute) and angular velocity. This conversion is essential in various fields, including physics, kinematics, and engineering. To simplify this process, we have developed the RPM to Angular Velocity Converter tool.
To use the RPM to Angular Velocity Converter, simply input the value of RPM into the designated field. The converter will then calculate the corresponding angular velocity in radians per second. This conversion factor is crucial for understanding the relationship between rotational speed and angular speed.
In circular motion, angular velocity represents the rate at which an object rotates around a fixed axis. It is measured in radians per second (rad/s). By converting RPM to angular velocity, we can determine the speed at which an object is rotating and its angular frequency.
To better understand the concept, let’s consider an example. Suppose we have a wheel rotating at 120 RPM. Using the RPM to Angular Velocity Converter, we can determine the angular velocity by inputting the value of 120 RPM. The converter will then provide us with the corresponding angular velocity in radians per second.
RPM to Angular Velocity Calculator
In addition to the RPM to Angular Velocity Converter, we also offer the RPM to Angular Velocity Calculator. This tool provides a convenient way to calculate the angular velocity based on the given RPM value. It is particularly useful when you need to perform multiple calculations or when you want to quickly verify your results.
To use the RPM to Angular Velocity Calculator, you simply need to enter the RPM value into the designated field. The calculator will then instantly display the corresponding angular velocity in radians per second. This allows you to quickly obtain the desired conversion without the need for manual calculations.
Understanding the relationship between RPM and angular velocity is crucial in various applications. For example, in rotational kinematics, the angular velocity is used to determine the rotational velocity of an object. It is also related to the linear velocity and tangential velocity of an object in circular motion.
By utilizing the RPM to Angular Velocity Converter and Calculator, you can easily perform the necessary conversions and gain a better understanding of rotational motion. These tools provide a simple and efficient way to convert between RPM and angular velocity, making it easier to analyze and solve problems related to circular velocity, wheel rotation, spin rate, and more.
Remember, whether you are studying physics, working on engineering projects, or simply curious about rotational motion, our RPM to Angular Velocity Converter and Calculator are here to assist you in your calculations.
Understanding RPM and Angular Speed
Rotational speed is an important concept in physics that helps us understand the motion of objects in circular or rotational motion. One common unit used to measure rotational speed is revolutions per minute (RPM). On the other hand, angular speed is a measure of how quickly an object rotates around a fixed axis. In this article, we will explore the relationship between RPM and angular speed, as well as how angular speed affects the rotation of a body.
Relationship between RPM and Angular Speed
The relationship between RPM and angular speed is quite straightforward. RPM measures the number of complete revolutions an object makes in one minute, while angular speed measures the rate at which an object rotates in radians per second. To convert from RPM to angular speed, we need to use a conversion factor.
The conversion factor between RPM and angular speed is given by the formula:
Angular Speed (in radian per second) = RPM * (2π/60)
Here, 2π represents the number of radians in one complete revolution, and 60 is the number of seconds in one minute. By multiplying the RPM value by this conversion factor, we can obtain the corresponding angular speed in radian per second.
How Angular Speed Affects the Rotation of a Body
Angular speed plays a crucial role in determining the motion of a rotating body. It affects various aspects of rotational motion, including the rotational velocity, linear velocity, and tangential velocity of the object.
The rotational velocity of an object is directly proportional to its angular speed. As the angular speed increases, the object rotates faster, covering a larger angular displacement in a given time. This relationship can be described by the equation:
Rotational Velocity = Angular Speed * Radius
where the radius represents the distance from the axis of rotation to a point on the object.
Similarly, the linear velocity of a point on a rotating object is also influenced by the angular speed. The linear velocity is given by the equation:
Linear Velocity = Angular Speed * Radius
This equation shows that the linear velocity of a point on the object is directly proportional to the angular speed and the distance from the axis of rotation.
Lastly, the tangential velocity of a point on a rotating object is equal to the linear velocity of that point. Therefore, the tangential velocity is also affected by the angular speed. As the angular speed increases, the tangential velocity of the point increases as well.
In summary, understanding the relationship between RPM and angular speed is essential in analyzing the motion of rotating objects. By converting between these units and considering the effects of angular speed on rotational and linear velocities, we can gain valuable insights into the dynamics of circular motion.
Now that we have explored the relationship between RPM and angular speed, as well as how angular speed affects the rotation of a body, we can apply these concepts to solve various problems in rotational kinematics and circular motion. Whether it’s calculating the rotational velocity of a spinning wheel or analyzing the spin rate of a cycle per second, the motion equations and principles of angular speed will guide us in understanding the dynamics of rotational motion.
Exploring the Connection between RPM and Angular Velocity
Angular velocity and revolutions per minute (RPM) are two important concepts in physics that describe the rotational motion of an object. Understanding the relationship between RPM and angular velocity is crucial in various fields, including mechanics, engineering, and even sports. In this article, we will delve into the factors that influence this relationship and explore the conversion between RPM and angular velocity.
Factors Influencing the RPM-Angular Velocity Relationship
Several factors play a role in determining the relationship between RPM and angular velocity. Let’s take a closer look at each of these factors:
-
Conversion Factor: To convert RPM to angular velocity, we need to use a conversion factor. This factor depends on the units used to measure RPM and angular velocity. For example, if RPM is measured in revolutions per minute and angular velocity is measured in radians per second, the conversion factor is 2π/60. This conversion factor allows us to relate the linear motion of an object to its rotational motion.
-
Circular Motion: The relationship between RPM and angular velocity becomes evident when considering circular motion. When an object moves in a circular path, it undergoes both linear and rotational motion simultaneously. The angular velocity describes the rate at which the object rotates around its axis, while the RPM indicates the number of complete rotations the object makes in one minute.
-
Rotational Kinematics: The motion equations for rotational kinematics provide a mathematical framework to understand the relationship between RPM and angular velocity. These equations relate the angular displacement, angular velocity, and angular acceleration of an object in rotational motion. By manipulating these equations, we can determine the angular velocity of an object given its RPM or vice versa.
-
Linear Velocity: The linear velocity of an object on the edge of a rotating wheel or disk is related to its angular velocity. This relationship is given by the formula v = rω, where v represents the linear velocity, r is the radius of the wheel, and ω is the angular velocity. As the angular velocity increases, the linear velocity also increases, resulting in faster motion along the edge of the wheel.
-
Tangential Velocity: Tangential velocity is another term used to describe the linear velocity of an object moving in a circular path. It represents the speed of an object at a specific point on its circular trajectory. The tangential velocity is directly proportional to the angular velocity and the radius of the circular path. As the angular velocity increases, the tangential velocity also increases.
-
Spin Rate: The spin rate of an object refers to the number of complete rotations it makes in a given time period. This spin rate is commonly measured in RPM. By knowing the spin rate, we can determine the angular velocity of the object using the conversion factor mentioned earlier.
Understanding the connection between RPM and angular velocity is essential in various applications. Whether it’s analyzing the performance of a rotating machine or calculating the speed of a spinning wheel, knowing how these two concepts relate to each other allows us to make accurate predictions and calculations in the field of physics and kinematics.
In conclusion, the relationship between RPM and angular velocity is influenced by factors such as the conversion factor, circular motion, rotational kinematics, linear velocity, tangential velocity, and spin rate. By understanding these factors and their interplay, we can gain a deeper understanding of rotational motion and its connection to linear motion.
Converting Revolutions per Minute to Angular Velocity
Detailed Explanation of the Conversion Steps
Converting revolutions per minute (RPM) to angular velocity is a fundamental concept in physics and kinematics. It allows us to understand the rotational motion of objects and calculate their angular speed in radians per second. By converting RPM to angular velocity, we can analyze circular motion, rotational kinematics, and various other aspects of rotational dynamics.
To convert RPM to angular velocity, we need to use a conversion factor. The conversion factor is derived from the relationship between the number of revolutions and the number of radians in a complete circle. In one revolution, there are 2π radians. Therefore, the conversion factor is 2π radians per revolution.
To convert RPM to angular velocity, we can use the following formula:
Angular Velocity (in radians per second) = RPM * (2π radians/revolution) * (1 minute/60 seconds)
Let’s understand this conversion process with an example. Suppose we have a wheel rotating at a speed of 120 RPM. We can calculate its angular velocity as follows:
Angular Velocity = 120 RPM * (2π radians/revolution) * (1 minute/60 seconds)
Simplifying the equation, we get:
Angular Velocity = 120 * (2π/60) radians per second
Calculating the value, we find that the angular velocity of the wheel is approximately 12.57 radians per second.
Importance of Understanding the Units Involved
Understanding the conversion from RPM to angular velocity is crucial in various fields, especially in physics and engineering. Here are a few reasons why it is important to grasp this concept:
-
Analysis of Rotational Motion: Converting RPM to angular velocity allows us to analyze the rotational motion of objects. By understanding the angular speed in radians per second, we can determine the rate at which an object is rotating and study its behavior.
-
Application in Circular Motion: Angular velocity is essential in studying circular motion. It helps us calculate the rotational velocity and the linear velocity of objects moving in circular paths. These calculations are vital in fields such as astronomy, mechanics, and sports.
-
Motion Equations: Converting RPM to angular velocity is necessary when dealing with motion equations involving rotational kinematics. By converting the units, we can apply the appropriate formulas and solve problems related to rotational dynamics.
-
Interchangeability with Linear Velocity: Understanding the conversion between RPM and angular velocity allows us to relate rotational motion to linear motion. By knowing the tangential velocity of an object in circular motion, we can determine its linear velocity and vice versa.
By grasping the concept of converting RPM to angular velocity, we can gain a deeper understanding of rotational dynamics and its applications in various fields. It enables us to analyze the spin rate, cycle per second, and circular velocity of rotating objects, providing valuable insights into their behavior and characteristics.
Remember, RPM and angular velocity are interconnected, and being able to convert between the two units is essential for anyone studying or working with rotational motion.
RPM to Angular Velocity in Rad/s
Understanding the Unit of Radian per Second (rad/s)
When it comes to rotational motion, understanding the unit of radian per second (rad/s) is crucial. Radian per second is a unit used to measure angular velocity, which represents how fast an object is rotating. It is derived from the concept of circular motion, where one complete revolution around a circle is equal to 2π radians.
In physics and kinematics, angular velocity is often expressed in rad/s because it provides a more accurate representation of the rotational speed. Unlike revolutions per minute (RPM), which measures the number of complete rotations in a minute, rad/s focuses on the actual angular displacement per unit of time. This unit allows us to analyze rotational motion more precisely and make calculations using motion equations specific to rotational kinematics.
Significance of Expressing Angular Velocity in Rad/s
Expressing angular velocity in rad/s has several significant advantages. Firstly, it allows for easier comparison and conversion between different units of rotational speed. By using the conversion factor of 2π rad/s = 1 revolution per second, we can easily convert between rad/s and RPM.
Secondly, rad/s provides a direct link between angular velocity and linear velocity. In circular motion, the linear velocity of an object on the edge of a rotating wheel is equal to the product of its angular velocity (in rad/s) and the radius of the wheel. This relationship is crucial in understanding the tangential velocity of objects in rotational motion.
Lastly, expressing angular velocity in rad/s enables us to apply the principles of frequency and period. Angular frequency, measured in rad/s, is the number of complete cycles per second. It is related to angular velocity through the equation ω = 2πf, where ω is the angular frequency and f is the frequency in cycles per second.
Example: Converting 45 RPM to Angular Velocity
Let’s take an example to understand how to convert RPM to angular velocity in rad/s. Suppose we have a wheel rotating at a speed of 45 RPM. To convert this to rad/s, we can use the conversion factor mentioned earlier: 2π rad/s = 1 revolution per second.
Using this conversion factor, we can calculate the angular velocity as follows:
Angular velocity (in rad/s) = 45 RPM * (2π rad/s) / (1 revolution per minute)
Simplifying the equation, we get:
Angular velocity = 45 * 2π / 60 rad/s
Angular velocity ≈ 4.71 rad/s
Therefore, a wheel rotating at 45 RPM has an angular velocity of approximately 4.71 rad/s.
By converting RPM to rad/s, we can better understand the rotational motion of objects and apply the principles of angular velocity in various physics and engineering applications. Whether it’s analyzing the spin rate of a wheel or calculating the circular velocity of an object, expressing angular velocity in rad/s provides a more accurate and comprehensive representation of rotational speed.
How to Find Angular Velocity from RPM
Exploring the Formula for Converting RPM to Angular Velocity
When it comes to understanding rotational motion, one important concept to grasp is the relationship between rotational speed and angular velocity. Rotational speed is commonly measured in revolutions per minute (RPM), while angular velocity is measured in radians per second (rad/s). In this guide, we will explore the formula for converting RPM to angular velocity and provide some tips for calculating angular velocity accurately.
To convert RPM to angular velocity, we need to use a conversion factor. The conversion factor is derived from the relationship between the circumference of a circle and the angle it subtends. In circular motion, one revolution corresponds to a complete circle, which is equivalent to 2π radians. Therefore, the conversion factor is 2π/60, since there are 60 seconds in a minute.
To calculate angular velocity (ω) from RPM, we can use the following formula:
ω = (2π/60) * RPM
Let’s say we have a wheel rotating at 120 RPM. To find its angular velocity, we can substitute the value of RPM into the formula:
ω = (2π/60) * 120
Simplifying the equation, we get:
ω = 4π rad/s
So, the angular velocity of the wheel is 4π rad/s.
Tips for Calculating Angular Velocity Accurately
Calculating angular velocity accurately is crucial in various fields of physics, such as kinematics and rotational motion. Here are some tips to help you calculate angular velocity with precision:
-
Understand the units: Make sure you are familiar with the units of rotational speed (RPM) and angular velocity (rad/s). Knowing the conversion factor and how to apply it correctly is essential.
-
Use the correct formula: The formula ω = (2π/60) * RPM is specifically used to convert RPM to angular velocity. Be sure to use this formula when performing calculations.
-
Convert units if necessary: If you are given rotational speed in units other than RPM, such as degrees per second or cycles per second, you may need to convert them to RPM before applying the formula. Use the appropriate conversion factors for accurate results.
-
Consider linear velocity: Angular velocity is related to linear velocity, which is the tangential velocity of an object moving in a circular path. If you know the radius of the circular path, you can use the formula v = ω * r to calculate the linear velocity.
-
Practice with motion equations: Familiarize yourself with the motion equations for rotational kinematics. These equations can help you solve problems involving angular velocity, acceleration, and time.
By following these tips, you can enhance your understanding of angular velocity and accurately calculate it in various scenarios. Remember to double-check your calculations and units to ensure precision in your results.
Now that you have a better understanding of how to find angular velocity from RPM and some tips for accurate calculations, you can confidently tackle problems involving rotational motion and circular velocity. Keep practicing and exploring the fascinating world of physics!
Frequently Asked Questions
What is the Relationship between Angular Velocity and RPM?
Angular velocity and RPM (revolutions per minute) are related to each other in circular motion. Angular velocity represents the rate at which an object rotates, while RPM measures the number of complete revolutions an object makes in one minute. The relationship between the two can be expressed using a conversion factor.
How do I Convert RPM to Angular Velocity in Radians per Second?
To convert RPM to angular velocity in radians per second, you can use the following formula:
Angular Velocity (in radians per second) = RPM * (2π/60)
Here, 2π represents the number of radians in one complete revolution, and 60 represents the number of seconds in one minute. By multiplying the RPM by the conversion factor, you can obtain the angular velocity in radians per second.
How do I Calculate the Angular Velocity for 80 RPM?
To calculate the angular velocity for 80 RPM, you can use the conversion formula mentioned earlier:
Angular Velocity (in radians per second) = 80 * (2π/60)
Simply substitute the value of 80 RPM into the formula and perform the calculation to find the angular velocity in radians per second.
Is there a Converter for RPM to Angular Velocity?
Yes, there are online converters available that can help you convert RPM to angular velocity. These converters usually require you to input the RPM value, and they will provide the corresponding angular velocity in radians per second. You can easily find these converters by searching online.
What is the Angular Velocity for 20 RPM?
To find the angular velocity for 20 RPM, you can use the same conversion formula mentioned earlier:
Angular Velocity (in radians per second) = 20 * (2π/60)
By substituting the value of 20 RPM into the formula and performing the calculation, you can determine the angular velocity in radians per second.
What is the Relationship between RPM and Angular Speed?
RPM and angular speed are closely related in circular motion. Angular speed represents the rate at which an object rotates, similar to angular velocity. The only difference is that angular speed is measured in radians per unit of time, while RPM measures the number of complete revolutions per minute. The relationship between RPM and angular speed can be established using the conversion factor mentioned earlier.
How can I Convert Revolutions per Minute to Angular Velocity?
To convert revolutions per minute (RPM) to angular velocity, you can use the conversion formula:
Angular Velocity (in radians per second) = RPM * (2π/60)
By multiplying the RPM value by the conversion factor, you can obtain the angular velocity in radians per second.
Is there a Calculator to Convert RPM to Angular Velocity?
Yes, there are online calculators available that can help you convert RPM to angular velocity. These calculators typically require you to input the RPM value, and they will provide the corresponding angular velocity in radians per second. You can easily find these calculators by searching online.
Remember, understanding the relationship between rotational speed, revolutions per minute, and angular velocity is essential in the study of circular motion and rotational kinematics. By utilizing the appropriate conversion factors and motion equations, you can easily convert between RPM and angular velocity to analyze various aspects of rotational motion.
How do I Convert Rev/min to Angular Velocity?
Converting revolutions per minute (RPM) to angular velocity is a straightforward process that involves a simple conversion factor. Angular velocity is a measure of how quickly an object rotates or moves in a circular path. It is commonly used in physics and kinematics to describe rotational motion.
To convert RPM to angular velocity, you need to multiply the rotational speed by a conversion factor. The conversion factor depends on the units you want to convert to. In this case, we want to convert RPM to radians per second (rad/s), which is a commonly used unit for angular velocity.
The conversion factor for converting RPM to rad/s is given by:
Conversion Factor: 1 RPM = (2π/60) rad/s
This conversion factor is derived from the fact that there are 2π radians in one revolution and 60 seconds in one minute. By multiplying the RPM value by this conversion factor, we can obtain the corresponding angular velocity in rad/s.
Let’s take a specific example to illustrate this conversion.
What is the Angular Velocity for 2500 RPM?
To find the angular velocity for 2500 RPM, we can use the conversion factor mentioned earlier.
Given:
Rotational speed (RPM) = 2500 RPM
Conversion:
Angular velocity (rad/s) = 2500 RPM * (2π/60) rad/s
Simplifying the equation, we get:
Angular velocity (rad/s) = 2500 * (2π/60) rad/s
Calculating this expression, we find:
Angular velocity (rad/s) ≈ 261.799 rad/s
Therefore, the angular velocity for 2500 RPM is approximately 261.799 rad/s.
It’s important to note that angular velocity is a vector quantity, meaning it has both magnitude and direction. The direction of angular velocity depends on the direction of rotation. In this case, since we are only given the magnitude of the RPM, the direction of the angular velocity is not specified.
In addition to angular velocity, it is also common to consider other related quantities in rotational motion. These include rotational frequency (also known as angular frequency), rotational velocity, linear velocity, and tangential velocity. These quantities are interconnected through various motion equations and can be used to describe different aspects of circular motion and rotational kinematics.
So, whenever you need to convert RPM to angular velocity, remember to use the conversion factor of (2π/60) rad/s. This will allow you to accurately determine the angular velocity in rad/s for a given rotational speed in RPM.
Conclusion
In conclusion, understanding the concept of RPM (revolutions per minute) and angular velocity is crucial in various fields, including physics, engineering, and mechanics. RPM measures the number of complete rotations an object makes in one minute, while angular velocity measures the rate at which an object rotates in radians per second.
By converting RPM to angular velocity, we can determine the speed at which an object is rotating in a more precise and standardized unit. This conversion is done by multiplying the RPM value by 2π and dividing it by 60.
Having a clear understanding of RPM to angular velocity conversion allows us to analyze and calculate rotational motion accurately, making it an essential concept for anyone working with rotating objects or studying rotational dynamics.
How is angular velocity related to linear velocity?
Angular velocity and linear velocity are two concepts that are connected in the context of motion. Angular velocity refers to the rate at which an object rotates around a specific axis, while linear velocity represents the rate at which an object moves along a straight path. To understand the relationship between these two, it is important to explore how angular velocity is converted into linear velocity and vice versa. The article “Angular Velocity vs Linear Velocity: Explained” provides a detailed explanation of this connection and offers insights into the calculations and conversions involved.
Frequently Asked Questions
1. How do you calculate RPM from angular velocity?
To calculate RPM (Revolutions Per Minute) from angular velocity, you need to use the conversion factor. Angular velocity is typically measured in radians per second. To convert it to RPM, you divide the angular velocity by 2π (which is the radian equivalent of one revolution) and then multiply by 60 (to convert seconds to minutes).
2. Is RPM the same as angular velocity?
No, RPM and angular velocity are not the same, although they are related. RPM is a measure of how many times an object rotates around a circle in one minute, while angular velocity is a measure of the speed of rotation, typically expressed in radians per second.
3. What is the formula to convert RPM to angular velocity?
The formula to convert RPM to angular velocity is ω = RPM * 2π / 60, where ω is the angular velocity. This formula takes the RPM, multiplies it by 2π to convert revolutions to radians, and then divides by 60 to convert minutes to seconds.
4. How do you convert 20 RPM to angular velocity?
To convert 20 RPM to angular velocity, use the formula ω = RPM * 2π / 60. Substituting 20 for RPM gives ω = 20 * 2π / 60 = approximately 2.09 radians per second.
5. What is the relationship between angular velocity and RPM?
Angular velocity and RPM are both measures of rotational speed. They are related by the formula ω = RPM * 2π / 60, where ω is the angular velocity. This formula converts RPM to radians per second, which is the standard unit for angular velocity.
6. How do you convert 2500 RPM to angular velocity?
To convert 2500 RPM to angular velocity, use the formula ω = RPM * 2π / 60. Substituting 2500 for RPM gives ω = 2500 * 2π / 60 = approximately 261.8 radians per second.
7. Does angular velocity increase with radius?
No, angular velocity does not increase with radius. In circular motion, the angular velocity is independent of the radius. However, the linear or tangential velocity, which is the velocity of a point moving along the circumference, does increase with radius.
8. How do you convert RPM to angular velocity in radians per second?
To convert RPM to angular velocity in radians per second, use the formula ω = RPM * 2π / 60. This formula takes the RPM, multiplies it by 2π to convert revolutions to radians, and then divides by 60 to convert minutes to seconds.
9. How do you convert 400 RPM to angular velocity?
To convert 400 RPM to angular velocity, use the formula ω = RPM * 2π / 60. Substituting 400 for RPM gives ω = 400 * 2π / 60 = approximately 41.89 radians per second.
10. How do you find RPM given angular velocity?
To find RPM given angular velocity, you can use the formula RPM = ω * 60 / 2π, where ω is the angular velocity. This formula takes the angular velocity in radians per second, multiplies it by 60 to convert seconds to minutes, and then divides by 2π to convert radians to revolutions.
Also Read:
- How to find acceleration on a velocity vs time graph
- How to calculate velocity of string
- How to find orbital velocity of satellites
- How to calculate group velocity in wave mechanics
- How to find velocity in aerodynamics
- What is constant in velocity time graph
- How to find initial velocity
- Constant velocity example
- How to measure velocity in redshift observations
- How to derive velocity in chaos theory