The speed of light in a vacuum is a fundamental constant in physics, with a value of approximately 299,792 kilometers per second. According to the theory of special relativity, this speed is the same for all observers, regardless of their relative motion or the motion of the light source. Understanding the relationship between relative velocity and the speed of light is crucial for comprehending various phenomena in the realm of modern physics.
Reference Frames and Relative Velocity
When measuring the relative velocity between two objects, it is essential to specify the reference frame. A reference frame is a point of view from which events are observed. For example, if a train is moving at 40 m/s relative to the train track, the same train is stationary relative to a passenger on the train.
The relative velocity between two objects is the difference in their velocities as measured from a specific reference frame. This relative velocity can be calculated using the formula:
$v_{rel} = v_2 – v_1$
where $v_{rel}$ is the relative velocity, $v_2$ is the velocity of the second object, and $v_1$ is the velocity of the first object.
The Speed of Light Limit
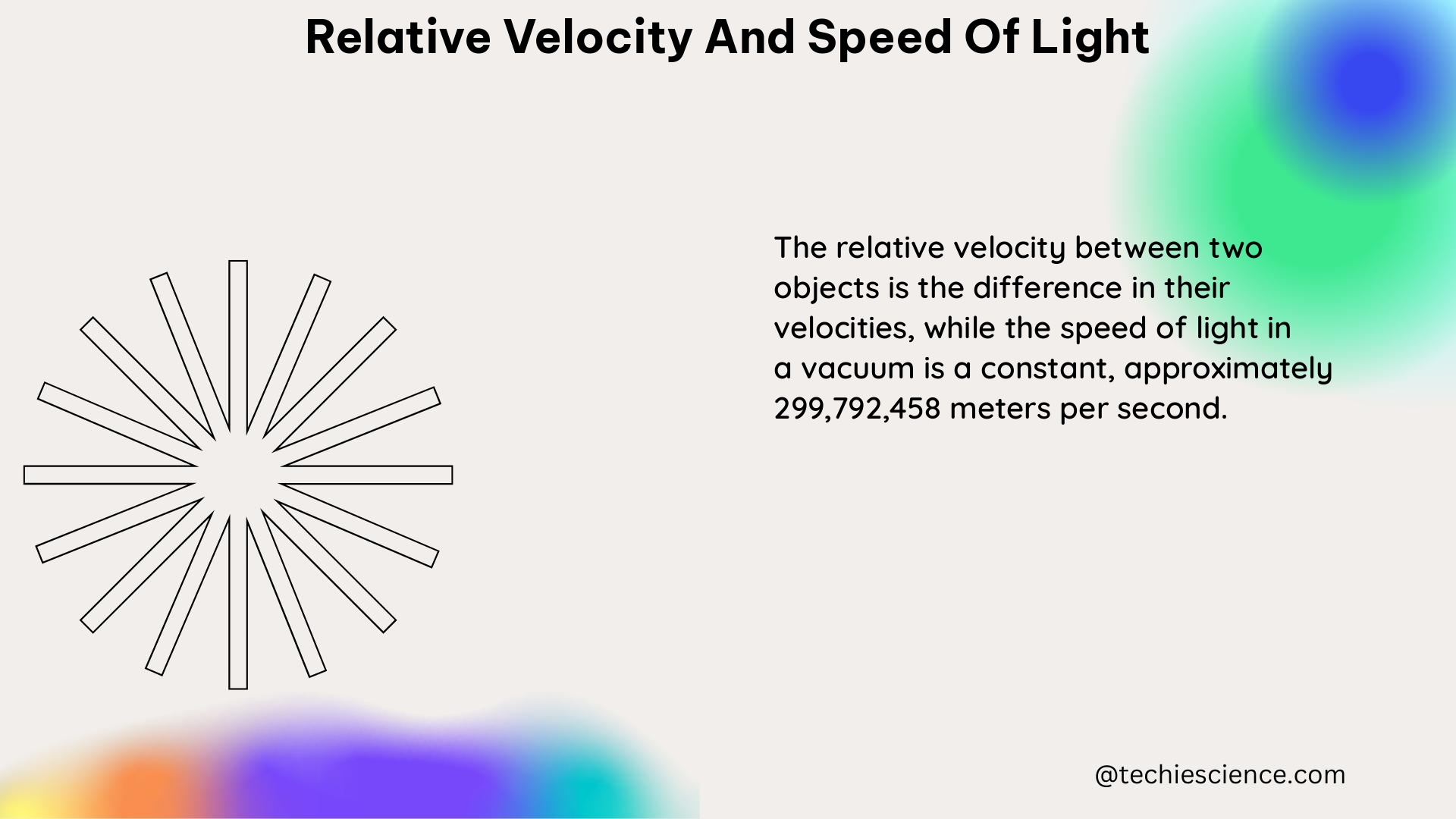
In the context of the speed of light, the relative velocity between two objects cannot exceed the speed of light. This is a fundamental principle of special relativity, known as the speed of light limit. However, it is possible for the relative velocity to appear to exceed the speed of light from a particular observer’s perspective. This apparent violation of the speed of light limit is a result of two key concepts in special relativity: time dilation and length contraction.
Time Dilation
Time dilation refers to the phenomenon where a moving observer’s clock will appear to tick slower than a stationary observer’s clock. This effect is described by the following equation:
$t’ = \gamma t$
where $t’$ is the time measured by the moving observer, $t$ is the time measured by the stationary observer, and $\gamma = \frac{1}{\sqrt{1 – \frac{v^2}{c^2}}}$ is the Lorentz factor.
Length Contraction
Length contraction, on the other hand, means that a moving object will appear shorter in the direction of motion to a stationary observer. The equation for length contraction is:
$L’ = \frac{L}{\gamma}$
where $L’$ is the length measured by the moving observer, $L$ is the length measured by the stationary observer, and $\gamma$ is the Lorentz factor.
Apparent Violation of the Speed of Light Limit
When combining the effects of time dilation and length contraction, the relative velocity between two objects can appear to exceed the speed of light from a particular observer’s perspective. This is known as the “apparent” violation of the speed of light limit.
For example, consider two objects moving towards each other at 55% the speed of light. From the perspective of a stationary observer, the closing velocity between the two objects would be 110% of the speed of light. However, this does not actually violate the speed of light limit, as it is a result of the way that time and space are perceived by the moving observers.
Numerical Problems
- Spaceship Traveling Away from Earth
- A spaceship is traveling away from Earth at 99% the speed of light.
- An astronaut on the spaceship sends a signal back to Earth.
- Question: How much time will pass on Earth between the moment the signal is sent and the moment it is received?
To solve this problem, we can use the time dilation equation:
$t’ = \gamma t$
where $t’$ is the time measured by the moving observer (the astronaut on the spaceship), $t$ is the time measured by the stationary observer (on Earth), and $\gamma = \frac{1}{\sqrt{1 – \frac{v^2}{c^2}}}$ is the Lorentz factor.
Given:
– Velocity of the spaceship: $v = 0.99c$
– Speed of light: $c = 299,792 \text{ km/s}$
Calculating the Lorentz factor:
$\gamma = \frac{1}{\sqrt{1 – \frac{(0.99c)^2}{c^2}}} = \frac{1}{\sqrt{1 – 0.9801}} = 7.089$
Therefore, the time that passes on Earth between the moment the signal is sent and the moment it is received is:
$t = \frac{t’}{7.089}$
This means that for every 7.089 seconds that pass on the spaceship, only 1 second will pass on Earth.
Figures, Data Points, and Measurements
- Speed of light in a vacuum: approximately 299,792 kilometers per second
- Time dilation: affects the perception of time for moving observers
- Length contraction: affects the perception of length for moving observers
Reference Links
- Special Relativity – Mr. Landgreen
- Relative velocity greater than speed of light – Physics Stack Exchange
- Measuring The Relative Velocity Of Light – Physics Forums
- Special Relativity – Physics LibreTexts
- The Speed of Light and Statics of Gravitational Field – Albert Einstein
This comprehensive guide on relative velocity and the speed of light covers the fundamental concepts, technical specifications, physics formulas, examples, and numerical problems. By understanding the principles of reference frames, time dilation, and length contraction, you can gain a deeper appreciation for the complex relationship between these two essential aspects of modern physics.