Torque and moment of inertia are fundamental concepts in the study of rotational motion, which is a crucial aspect of classical mechanics. Understanding these two quantities and their relationship is essential for solving a wide range of physics problems, from the motion of celestial bodies to the design of machinery and engineering systems.
Understanding Torque
Torque is a measure of the force that can cause an object to rotate about an axis. It is calculated as the cross product of the force and the distance from the axis to the point of application of the force. The unit of torque is the newton-meter (Nm).
The formula for calculating torque is:
τ = r × F
where:
– τ is the torque
– r is the distance from the axis of rotation to the point of application of the force
– F is the applied force
Torque can be thought of as the “twisting” or “turning” effect of a force on an object. The magnitude of the torque depends on the magnitude of the force, the distance from the axis of rotation, and the angle between the force and the line connecting the axis to the point of application.
Theorem: Torque and Angular Acceleration
The relationship between torque and angular acceleration is given by the equation:
τ = Iα
where:
– τ is the torque
– I is the moment of inertia
– α is the angular acceleration
This equation is known as the rotational analog of Newton’s second law of motion. It states that the torque acting on an object is equal to the product of its moment of inertia and its angular acceleration.
Examples of Torque Calculations
- Rotating a door: Consider a door with a mass of 10 kg and a length of 2 meters. If a force of 20 N is applied at a distance of 1 meter from the hinge, the torque acting on the door is:
τ = r × F = (1 m) × (20 N) = 20 Nm
- Tightening a nut with a wrench: Suppose you are using a wrench with a length of 0.5 meters to tighten a nut. If you apply a force of 50 N perpendicular to the wrench, the torque applied to the nut is:
τ = r × F = (0.5 m) × (50 N) = 25 Nm
- Rotating a pulley: A pulley with a radius of 0.2 meters is connected to a weight of 5 kg. If the weight is pulled with a force of 10 N, the torque acting on the pulley is:
τ = r × F = (0.2 m) × (10 N) = 2 Nm
These examples illustrate how the magnitude and direction of the applied force, as well as the distance from the axis of rotation, determine the torque acting on an object.
Understanding Moment of Inertia
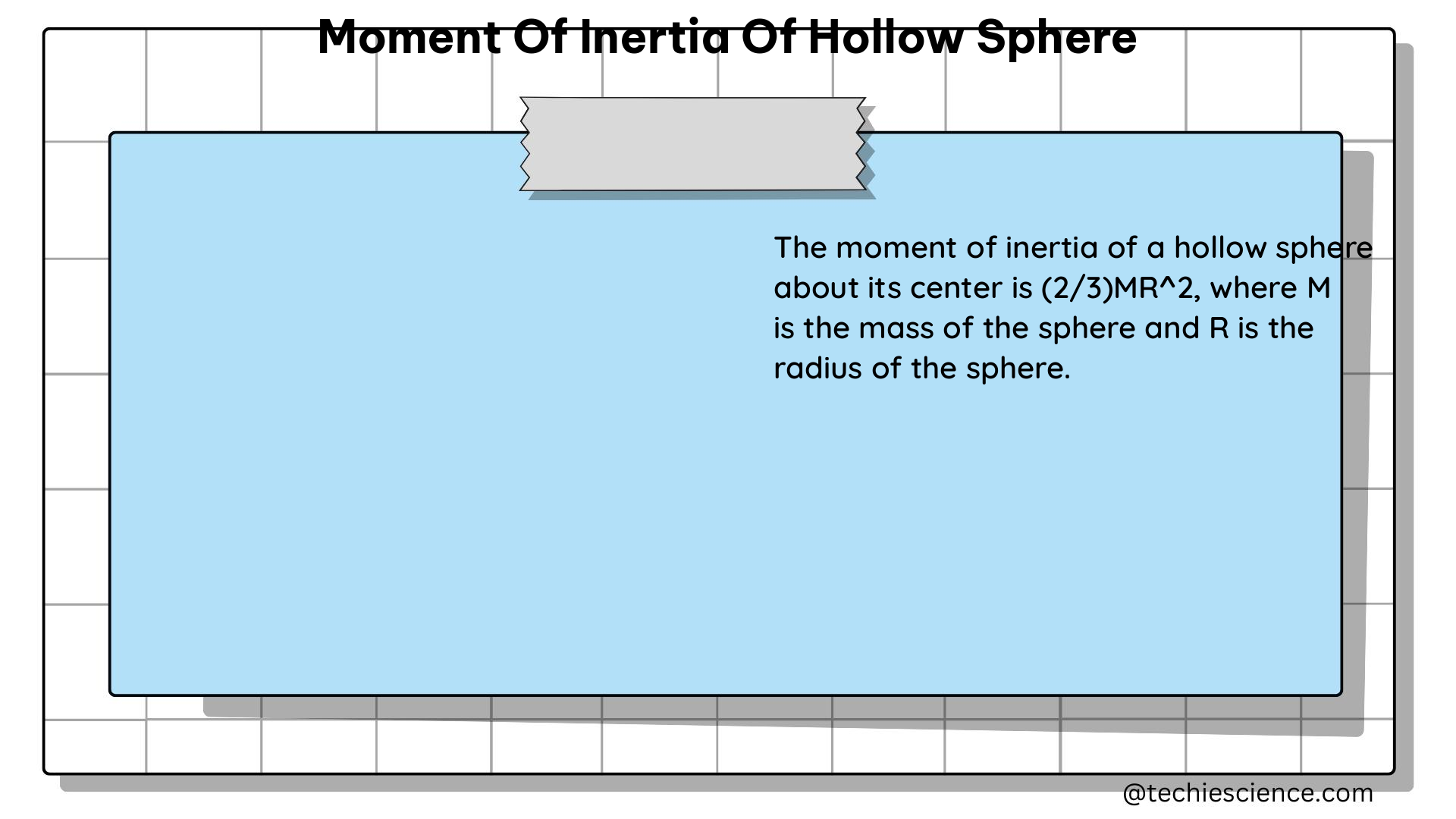
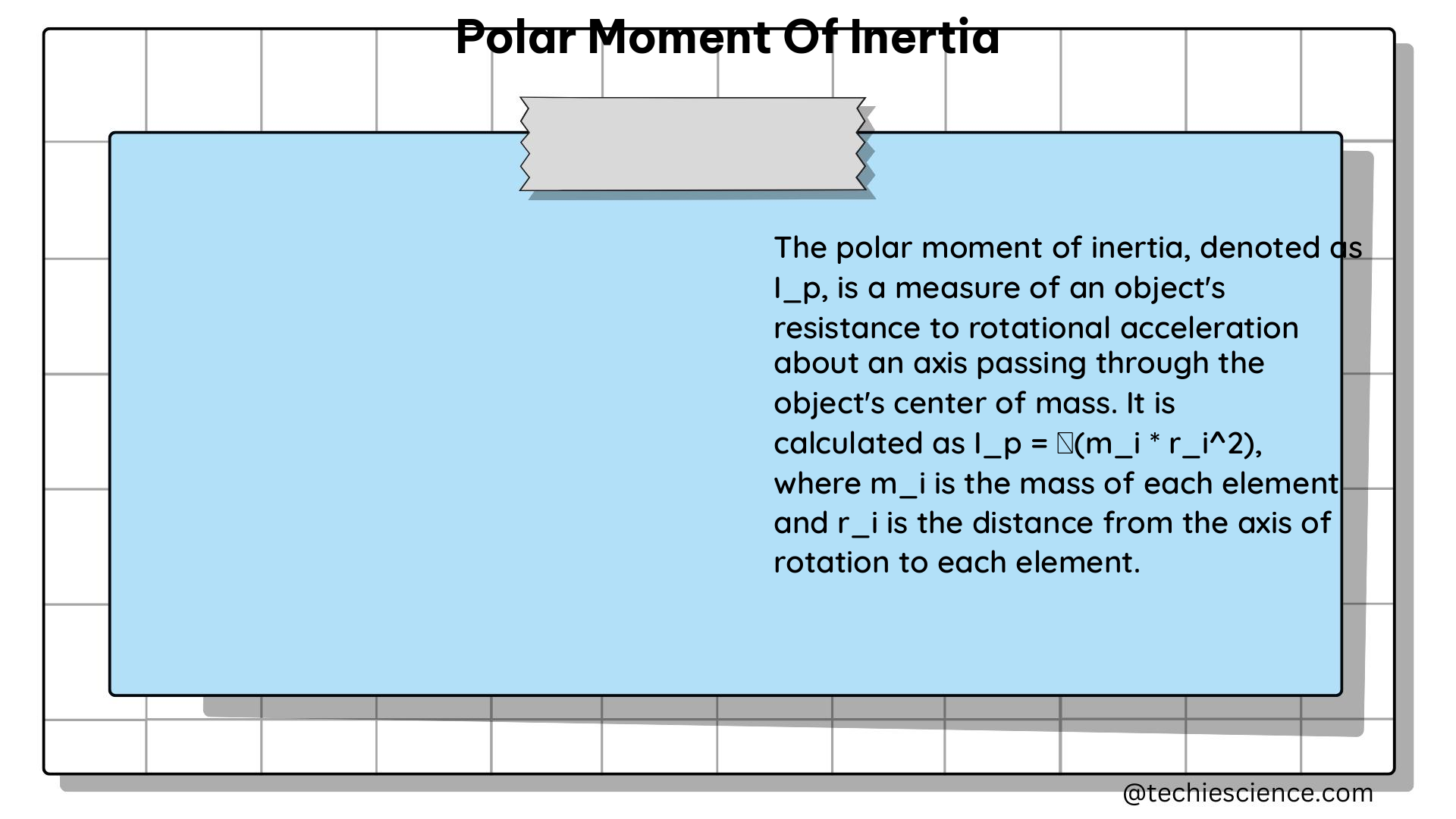
Moment of inertia, on the other hand, is a measure of an object’s resistance to rotational motion. It is calculated as the sum of the products of the mass of each particle in the object and the square of its distance from the axis of rotation. The unit of moment of inertia is kilogram-meter squared (kgm^2).
The formula for calculating the moment of inertia of a system of particles is:
I = Σ m_i r_i^2
where:
– I is the moment of inertia
– m_i is the mass of the i-th particle
– r_i is the distance of the i-th particle from the axis of rotation
Theorem: Moment of Inertia for Common Shapes
The moment of inertia for some common geometric shapes can be calculated using the following formulas:
-
Solid cylinder about its central axis:
I = (1/2) m r^2 -
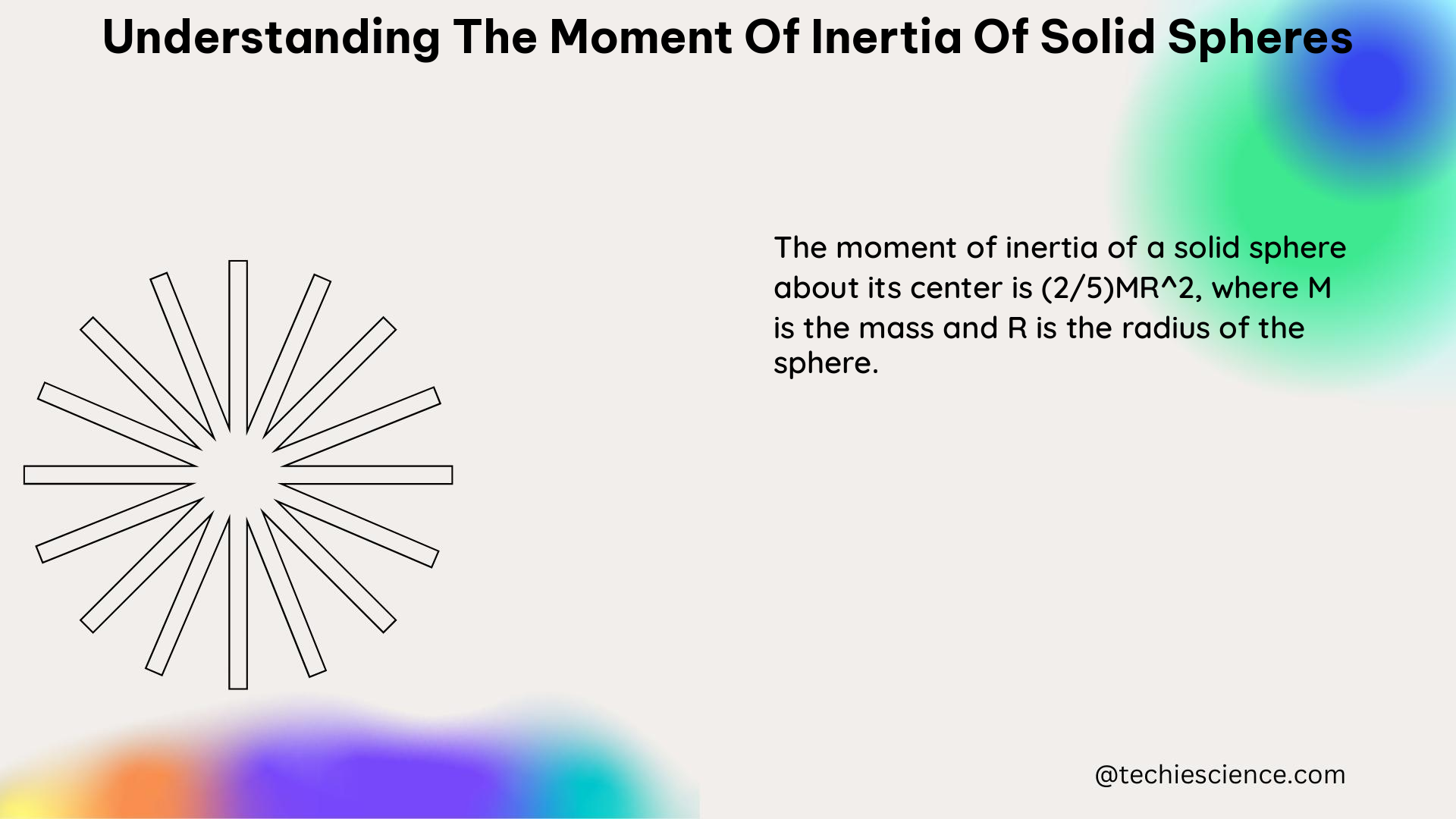
Solid sphere about its central axis:
I = (2/5) m r^2 -
Solid rod about an axis perpendicular to the rod and passing through its center:
I = (1/12) m L^2 -
Solid rectangular plate about an axis perpendicular to the plate and passing through its center:
I = (1/12) m (L^2 + W^2)
where:
– m is the mass of the object
– r is the radius of the cylinder or sphere
– L is the length of the rod or plate
– W is the width of the rectangular plate
These formulas provide a convenient way to calculate the moment of inertia for common geometric shapes, which can be useful in a variety of physics problems.
Examples of Moment of Inertia Calculations
- Rotating a solid cylinder: Consider a solid cylinder with a mass of 5 kg and a radius of 0.3 meters. The moment of inertia of the cylinder about its central axis is:
I = (1/2) m r^2 = (1/2) × (5 kg) × (0.3 m)^2 = 0.225 kgm^2
- Rotating a solid sphere: Suppose you have a solid sphere with a mass of 2 kg and a radius of 0.1 meters. The moment of inertia of the sphere about its central axis is:
I = (2/5) m r^2 = (2/5) × (2 kg) × (0.1 m)^2 = 0.004 kgm^2
- Rotating a solid rod: Consider a solid rod with a mass of 1 kg and a length of 0.5 meters. The moment of inertia of the rod about an axis perpendicular to the rod and passing through its center is:
I = (1/12) m L^2 = (1/12) × (1 kg) × (0.5 m)^2 = 0.0208 kgm^2
These examples demonstrate how the moment of inertia of an object depends on its mass and the distribution of that mass relative to the axis of rotation.
Relationship between Torque and Moment of Inertia
The relationship between torque and moment of inertia is given by the equation:
τ = Iα
where:
– τ is the torque
– I is the moment of inertia
– α is the angular acceleration
This equation is the rotational analog of Newton’s second law of motion and is a fundamental principle in the study of rotational dynamics.
Physics Formulas Involving Torque and Moment of Inertia
-
Rotational Kinetic Energy:
Rotational kinetic energy = (1/2) I ω^2
where ω is the angular velocity of the object. -
Torque Required for Acceleration:
Torque required to accelerate an object from rest to an angular velocity ω in time t:
τ = (1/2) I ω^2 / t -
Torque Required for Deceleration:
Torque required to stop an object rotating at an angular velocity ω in time t:
τ = (1/2) I ω^2 / t -
Moment of Inertia of a System of Particles:
I = Σ m_i r_i^2
where m_i is the mass of the i-th particle and r_i is its distance from the axis of rotation.
These formulas demonstrate the important role that both torque and moment of inertia play in the analysis of rotational motion and the design of mechanical systems.
Numerical Problems and Exercises
-
Rotating a Flywheel: A flywheel with a moment of inertia of 0.5 kgm^2 is initially at rest. If a constant torque of 10 Nm is applied to the flywheel, calculate:
a. The angular acceleration of the flywheel.
b. The time it takes for the flywheel to reach an angular velocity of 50 rad/s. -
Stopping a Rotating Wheel: A wheel with a moment of inertia of 0.2 kgm^2 is rotating at an angular velocity of 30 rad/s. If a constant torque of 5 Nm is applied to stop the wheel, calculate:
a. The time it takes for the wheel to come to a complete stop.
b. The angular displacement of the wheel during the stopping process. -
Lifting a Load with a Pulley: A pulley with a radius of 0.1 meters and a moment of inertia of 0.01 kgm^2 is used to lift a load of 20 kg. If a force of 50 N is applied to the pulley, calculate:
a. The torque acting on the pulley.
b. The angular acceleration of the pulley.
c. The time it takes for the load to be lifted 2 meters. -
Rotating a Solid Cylinder: A solid cylinder with a mass of 10 kg and a radius of 0.2 meters is rotating about its central axis. If the cylinder is subjected to a constant torque of 5 Nm, calculate:
a. The moment of inertia of the cylinder.
b. The angular acceleration of the cylinder.
c. The time it takes for the cylinder to reach an angular velocity of 20 rad/s. -
Moment of Inertia of a Compound Object: A system consists of a solid cylinder with a mass of 5 kg and a radius of 0.1 meters, and a solid sphere with a mass of 3 kg and a radius of 0.05 meters. The objects are connected by a massless rod of length 0.2 meters. Calculate the moment of inertia of the system about an axis passing through the center of the cylinder and perpendicular to the rod.
These problems cover a range of applications of torque and moment of inertia in rotational motion, allowing you to practice and reinforce your understanding of these important concepts.
Conclusion
Torque and moment of inertia are fundamental quantities in the study of rotational motion, and a deep understanding of these concepts is essential for solving a wide range of physics problems. By mastering the formulas, theorems, and examples presented in this guide, you will be well-equipped to tackle complex problems involving the dynamics of rotating systems.
References
- OpenStax, University Physics Volume 1. https://openstax.org/books/university-physics-volume-1/pages/10-4-moment-of-inertia-and-rotational-kinetic-energy
- Raptor Scientific, Why Is Moment of Inertia Important? https://raptor-scientific.com/news/why-moi-is-important/
- Hoffner Physics, Moment of Inertia Lab. http://hoffnerphysics.weebly.com/moment-of-inertia-lab.html
- Serway, R. A., & Jewett, J. W. (2018). Physics for Scientists and Engineers with Modern Physics (10th ed.). Cengage Learning.
- Halliday, D., Resnick, R., & Walker, J. (2013). Fundamentals of Physics (10th ed.). Wiley.