Frequency

The Science of Pitch and Frequency: A Comprehensive Guide for Physics Students

by
pitch and frequency

Pitch and frequency are fundamental concepts in the study of sound and acoustics. Frequency, measured in Hertz (Hz), is the number of complete back-and-forth vibrations of a particle of the medium per unit of time. Pitch, on the other hand, is the subjective perception of the frequency of a sound wave. This comprehensive guide will … Read more

Boost Your Productivity: A Comprehensive Guide for Physics Students

by
boost your productivity

As a physics student, maximizing your productivity is crucial for academic success and personal growth. This comprehensive guide will provide you with a detailed roadmap to boost your productivity, drawing from various productivity measurement techniques and strategies tailored specifically for physics students. Measure Productivity Effectively 1. Monitor Profitability Profitability is a key indicator of productivity … Read more

Does Amplitude Change with Frequency?

by
does amplitude change with frequency

Amplitude and frequency are two fundamental properties of waves, and understanding their relationship is crucial in various fields of physics, engineering, and beyond. This comprehensive guide delves into the intricate details of how amplitude and frequency interact, providing a thorough exploration of the underlying principles, theoretical explanations, and practical applications.

Understanding Amplitude and Frequency

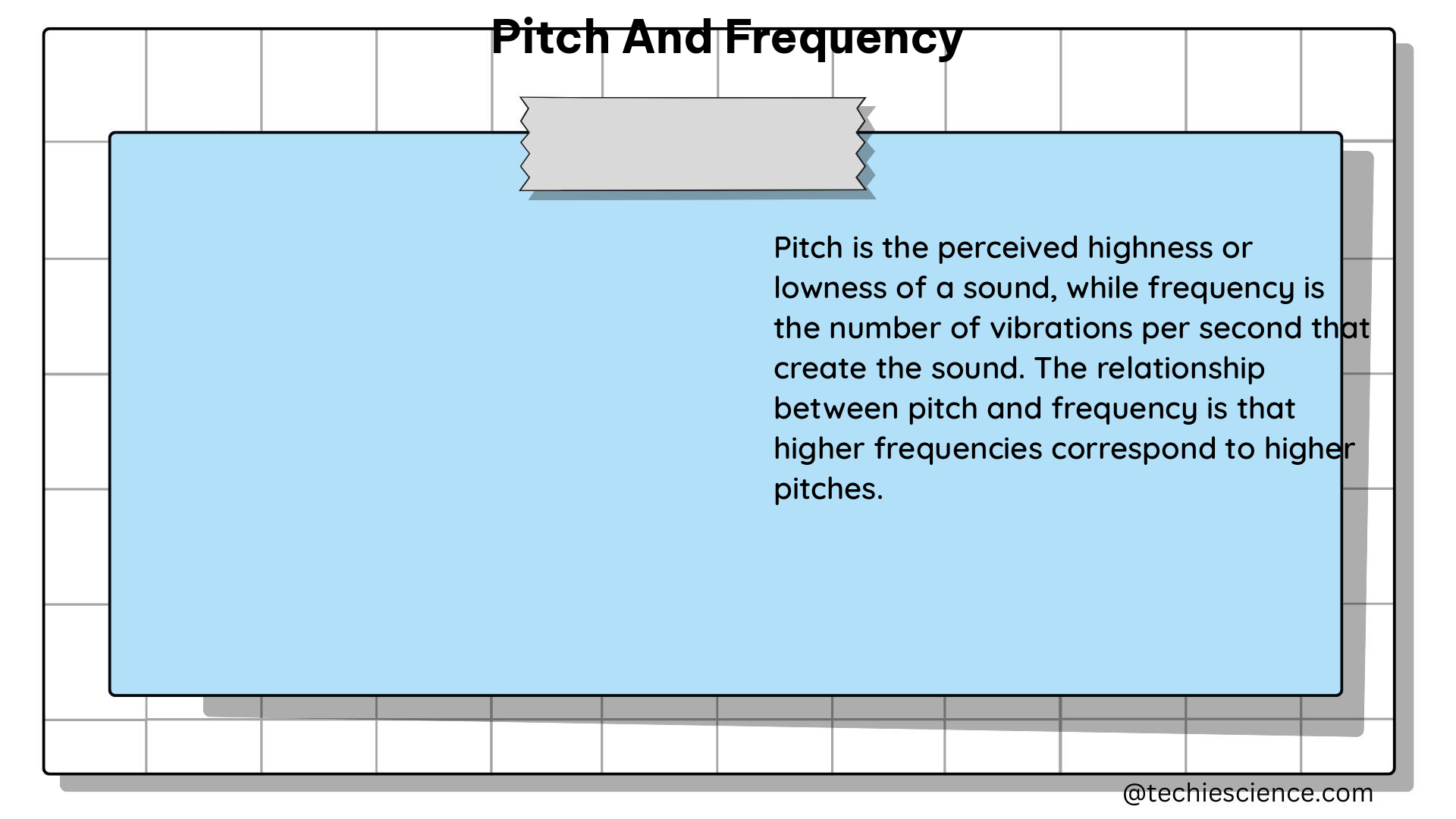
Amplitude refers to the maximum displacement of a wave from its equilibrium position, while frequency represents the number of oscillations or cycles per unit of time. These two properties are independent, meaning that changing the frequency of a wave does not inherently affect its amplitude, and vice versa.

The relationship between amplitude and frequency is described by the wave equation, which shows that they are multiplicative factors in the expression for a wave’s energy. Specifically, the energy of a wave is proportional to the square of both its amplitude and frequency. This means that altering the frequency of a wave while keeping its amplitude constant will result in a change in the wave’s energy, but not in its amplitude.

Theoretical Explanations

does amplitude change with frequency

The independence of amplitude and frequency can be understood through various theoretical explanations, including the analogy of a spring-mass system. When a spring is stretched or compressed and then released, it oscillates up and down with a certain amplitude and frequency, which are determined by the spring constant and the mass of the attached object. Increasing the frequency of the oscillations by changing the mass or spring constant does not affect the amplitude, unless there are other constraints or forces acting on the system.

Similarly, in the case of waves, the amplitude and frequency are determined by the properties of the medium and the source of the wave, and they can vary independently of each other, as long as there are no additional constraints or interactions. For example, in the case of electromagnetic waves, the amplitude corresponds to the electric field strength, while the frequency is determined by the wave’s wavelength and the speed of light. By changing the frequency of the wave, we can tune into different radio stations or observe different spectral lines in astronomical observations, without affecting the amplitude of the wave.

Exceptions and Constraints

While the general principle states that amplitude and frequency are independent properties, there are some cases where they can be related due to external factors or constraints. For instance, in the case of a string instrument, the amplitude and frequency of the sound waves produced by the instrument are related to the tension, mass, and length of the strings, as well as the force and duration of the pluck or strike. By changing the tension or the length of the strings, we can alter the frequency of the sound waves, but this will also affect the amplitude, due to the changes in the string’s vibrational properties.

Practical Applications and Implications

The independence of amplitude and frequency has important implications in various fields, such as:

  1. Physics: The principle of the independence of amplitude and frequency is a fundamental concept in wave physics, with applications in areas like optics, acoustics, and electromagnetism.

  2. Engineering: Understanding the relationship between amplitude and frequency is crucial in the design and analysis of various systems, such as communication systems, signal processing, and vibration analysis.

  3. Music and Acoustics: The independence of amplitude and frequency is a key principle in the production and perception of musical sounds, as it allows for the independent control of volume and pitch.

  4. Astronomy and Spectroscopy: The ability to change the frequency of electromagnetic waves without affecting their amplitude is essential for techniques like spectroscopy, which is used to study the composition of celestial objects.

Numerical Examples and Calculations

To further illustrate the independence of amplitude and frequency, let’s consider a few numerical examples and calculations:

  1. Electromagnetic Waves: Suppose we have an electromagnetic wave with a frequency of 100 MHz and an amplitude of 10 V/m. If we increase the frequency to 200 MHz, the amplitude will remain the same at 10 V/m, but the energy of the wave will increase by a factor of 4 (since the energy is proportional to the square of the frequency).

  2. Vibrating String: Consider a guitar string with a length of 0.6 m, a mass of 0.005 kg, and a tension of 100 N. The frequency of the fundamental mode of vibration is given by the formula: $f = \frac{1}{2L}\sqrt{\frac{T}{m}}$, where $L$ is the length of the string, $T$ is the tension, and $m$ is the mass. If we increase the tension to 200 N, the frequency will increase by a factor of $\sqrt{2}$, but the amplitude of the vibration will also change due to the change in the string’s properties.

  3. Sound Waves: Suppose we have a sound wave with a frequency of 1 kHz and an amplitude of 0.1 Pa. If we increase the frequency to 2 kHz, the amplitude will remain the same at 0.1 Pa, but the intensity of the sound wave (which is proportional to the square of the amplitude) will increase by a factor of 4.

These examples demonstrate the fundamental principle that amplitude and frequency are independent properties of waves, and that changing one does not inherently affect the other, unless there are external constraints or factors involved.

Conclusion

In summary, the amplitude and frequency of a wave are independent properties, meaning that changing the frequency of a wave does not affect its amplitude, and vice versa. This principle is supported by various theoretical explanations and experimental evidence, and it has important implications in numerous fields, such as physics, engineering, and music. While there are some cases where the amplitude and frequency can be related due to external factors or constraints, this is not a fundamental property of the wave itself.

References:

  • How does amplitude affect frequency of a wave? – Physics Stack Exchange
  • Relative Amplitude – an overview | ScienceDirect Topics
  • Does amplitude increase with an increase in frequency? – CK-12
  • Intensity – The Physics Hypertextbook
  • Does an amplitude change result in a frequency change? – Gearspace

What Is Oscillation Frequency: Interesting Facts and FAQs

by

Whether our vision can reach them or not, oscillations occur all around us. So, in this post, we’ll look at what is oscillation frequency, how to calculate oscillation frequency and oscillation frequency units.

The frequency of oscillations is a physical term that describes how many oscillations took place in a unit of time in an oscillating system such as a pendulum, spring mass system, or electronic system.

Before we go into what is oscillation frequency, let’s first define oscillation.

Oscillation:

Oscillation is a repeated variation in amplitude or position around a central point or equilibrium, with time following the same path.

A single oscillation is a complete movement over a period of time, which can be up and down or side to side. One cycle of oscillation is another name for it. The time it takes to complete one oscillation is the oscillation time period. Every oscillation is a periodic motion, but not all periodic motions are oscillations. Examples of oscillation are spring movement with mass, pendulum motion, the vibration of string instruments, etc.  

ลูกตุ้มธรรมชาติ 3
Oscillating Pendulum GIF Credits: Wikinana38, ลูกตุ้มธรรมชาติ, CC BY-SA 4.0

Oscillation frequency:

The oscillation frequency is the number of oscillations that repeat in unit time, i.e., one second. Taking reciprocal of time taken by oscillation will give the frequency of oscillation.

fudHMVq2rk5NSKFOlUsnNZDF3Qre7F3pO5RFRfAHEmK0So1a06Q9osPZ31urheNyN4ejXIhPL VpHt4uW QFzDigXEeYtTv50Sv9OAwwvrP2LfzVS1mJJ3mfWL kI271nyddfzTJ

fQfxZlgnktcw9aWsz43ai2d1orxjqOVCZA

To understand oscillation frequency, let’s consider a simple example of the guitar. While playing guitar, you pluck the string of a guitar. As the motion of the guitar string is repetitive for significant cycles, it is considered as oscillation. To complete one successive cycle time taken by the string is the same. Thus, if we take reciprocal of it, we get the frequency of guitar string oscillation. Suppose it takes 0.2 seconds to complete one cycle, then the number of oscillations in one second is five, which is the frequency of oscillating guitar strings.

5853120739 fca6e0b83b q
Image Credits: “Guitar strings close up” by richard_north , CC BY 2.0

Let us now look at the frequency of oscillation units.

Frequency of oscillation units:

The SI unit for the oscillation time period is the second (s). Because the reciprocal of the oscillation’s time period determines its frequency, its unit is the reciprocal of the time period’s unit, i.e., s-1.

Many unit names are inspired by the scientists who worked on the unit’s research. Heinrich Hertz, a German physicist, made a significant contribution to the field of electromagnetic radiation. As a result, Hertz is also regarded as a SI unit of frequency in honour of this famous scientist. As Hertz represents cycles per second, we can say that

1 Hertz = one cycle per second.

Thus, s and Hertz are frequency of oscillation units that are used as SI frequency units, but Hertz is more commonly used.

After going through what is oscillation frequency and frequency oscillation units, you might wonder how to calculate oscillation frequency. So let’s see how to calculate oscillation frequency.

How to calculate oscillation frequency?

There are two ways to calculate oscillation frequency:

  • Mathematical 
  • Experimental

⇒ A mathematical way to calculate oscillation frequency:

To calculate the frequency of an oscillation, we must utilize period and frequency formulas. The formulas for calculating oscillation frequency vary depending on the system.

✦ Oscillation frequency of spring mass system:

As shown in the figure, a mass m is attached to the end of the spring. Spring will oscillate up and down due to the weight of the mass. Thus, if k is the spring constant of spring, then the frequency of oscillating frequency is given by:

8w NcR4aLAzF Ap68RManYvsw6kuoH YNZGW5Mat swLCv35bXlUhgK2 ffY3txmRJ0rxC0 Non eY5J7tBmCwE4c2VU DzU3yi01vR8Zp2DWrGmS25EAe8ZrUv3YBYNOZ1mNDRg

What is oscillation frequency
GIF credits: Svjo, Animated-mass-spring, CC BY-SA 3.0

✦ Oscillation frequency of simple pendulum:

In a simple pendulum, mass m is attached to the end of the string. Thus, due to the mass, the string will oscillate back and forth. Therefore, if L is the length of the string, the frequency of the simple pendulum is given by:

Pendulum no text
GIF credits: Stündle (modification Ideophagous), Pendulum-no-text, CC BY-SA 4.0

Thus, we can say that in the case of a simple pendulum, the frequency of oscillation is not dependent on the mass of the attached object.

✦ Oscillation frequency of the compound or physical pendulum:

A physical or compound pendulum is formed by suspending a rigid body to the fixed horizontal axis. As the rigid body is involved, its moment of inertia I will also come into action. Thus, the frequency of the compound pendulum is given by:

dwe6CDr7JR5f9vHsklDMclA29DnpuxjJo4eXD3DzaGeqO6SJ8tdeUZL2vUZBKTKRvcS5 Y4qbwxXC633S4vBqUscMQXeYK hNbMmLy6 lZ sgc6zB0GYWE4BSmzsVk70eedPf6pc

✦ Oscillation frequency of the torsional pendulum:

When a disc-like mass is suspended from a wire or thin rod instead of a rigid body, the system is known as a torsional pendulum. As a result, the torsional pendulum oscillation frequency is:

ucRqBWgSho1w9EQIPzNN BuJ 5l DuPdUq0iYYgQMzrCczwSbD2h edFvDSKWS1kQpiMRn5T5hLItKHTerqx704VWsNTF4 Kdcm B iT6x4Tg39xm0ORfwjou YCiPSK92Weqwq6

⇒ An experimental way to calculate oscillation frequency:

The oscillation frequency calculation for a pendulum or a spring mass system is nearly identical. The main difference is that the spring constant k must be calculated for the spring mass system. The method is as follows:

  • In a spring mass system, to calculate the spring constant, hang the mass on the spring and the spring will start to oscillate. Now, allow the mass to come to a motionless state where the gravitational force of mass and spring force will be balanced. After that, adding mass to spring will stretch, so record this change in spring stretch.

 Δmg -kΔy =0

Thus, spring constant k is:

xJ MltUTOKTsJQK3gg4 9q4Km8AAlMMLaCItWyT wqtD4Zbl0 R6gCfd5MyHS aebioNwTLWaQPiGh7jZn9nQZD80XV3T 2sPztMshv0gf5d6YCTS2Zc2RT5vfSXTTcIrT3VPQAM

  Here, Δy is the change in spring stretch.

  • Oscillate the spring or pendulum now. Then, for each mass, keep track of the time for ten oscillations. To acquire an accurate response, repeat this method three times. The average of the three times will be used to determine the time period. Take the inverse of that and you’ll get the frequency.

We hope that this article has answered your questions about what oscillation frequency is, what oscillation frequency units are, and how to calculate oscillation.

Also Read:

Angular Frequency vs Frequency: A Comprehensive Guide for Physics Students

by
angular frequency vs frequency

Summary

Angular frequency and frequency are both measures of the rate of repetitive events, but they differ in their units and applications. Angular frequency, denoted by ω, is measured in radians per second (rad/s) and represents the rate of change of the phase angle of a periodic function. Frequency, denoted by f, is measured in cycles or oscillations per second (Hz) and represents the number of complete cycles or oscillations per unit time. The relationship between angular frequency and frequency is given by the equation ω = 2πf, which is crucial in understanding the dynamics of various physical systems.

Understanding Angular Frequency

angular frequency vs frequency

Angular frequency, ω, is a fundamental concept in classical mechanics and wave mechanics. It represents the rate of change of the phase angle of a periodic function, such as an oscillation or a wave. The phase angle is the angle between the current position of the periodic function and its initial position.

Characteristics of Angular Frequency

  • Measured in radians per second (rad/s)
  • Represents the ‘speed’ or rate of change of a periodic function
  • Significant in understanding the dynamics of oscillating systems and wave propagation
  • Closely related to the period (T) of the periodic function through the equation ω = 2π/T

Calculating Angular Frequency

The angular frequency of a system can be calculated using various formulas, depending on the specific physical situation. Some common examples include:

  1. Simple Harmonic Motion:
  2. For a mass-spring system, the angular frequency is given by ω = √(k/m), where k is the spring constant and m is the mass.

  3. Example: For a mass-spring system with k = 1.2 N/m and m = 0.4 kg, the angular frequency is ω = √(1.2/0.4) = 1.7 rad/s.

  4. Electromagnetic Waves:

  5. The angular frequency of an electromagnetic wave is used in the temporal part of the wave function, indicating the rate of change of the wave’s phase angle.
  6. Example: The angular frequency of a radio wave with a frequency of 100 MHz is ω = 2πf = 2π × 100 × 10^6 = 6.28 × 10^8 rad/s.

Understanding Frequency

Frequency, f, is a measure of the number of complete cycles or oscillations per unit time. It is commonly used to describe the repetition rate of events, such as the number of times a pendulum swings per second or the number of cycles per second in an electrical signal.

Characteristics of Frequency

  • Measured in cycles or oscillations per second (Hz)
  • Represents the number of complete cycles or oscillations per unit time
  • Commonly used to describe the repetition rate of events
  • Closely related to the period (T) of the periodic function through the equation f = 1/T

Calculating Frequency

The frequency of a periodic function can be calculated using the following formula:

f = 1/T

Where T is the period of the periodic function, which represents the time taken for one complete cycle or oscillation.

Example:
– A pendulum oscillates with a period of 0.5 seconds.
– The frequency of the pendulum is f = 1/T = 1/0.5 = 2 Hz.

Relationship Between Angular Frequency and Frequency

The relationship between angular frequency and frequency is given by the equation:

ω = 2πf

This equation indicates that angular frequency is equal to 2π times the frequency. This means that if the frequency increases, the angular frequency also increases, and vice versa.

Numerical Examples

  1. Pendulum Oscillation:
  2. A pendulum oscillates at a frequency of 2 Hz.

  3. The angular frequency of the pendulum is ω = 2πf = 2π × 2 = 4π rad/s.

  4. Spring-Mass System:

  5. A spring-mass system has a spring constant of 5 N/m and a mass of 20 kg.
  6. The angular frequency of the system is ω = √(k/m) = √(5/20) = 0.5 rad/s.

Theorems and Physics Formulas

  • ω = 2πf (Relationship between angular frequency and frequency)
  • ω = √(k/m) (Angular frequency of a mass-spring system)
  • T = 1/f (Relationship between period and frequency)
  • ω = 2π/T (Relationship between angular frequency and period)

Figures and Data Points

  • Angular frequency is measured in radians per second (rad/s)
  • Frequency is measured in cycles or oscillations per second (Hz)
  • The period of an oscillation is the reciprocal of the frequency: T = 1/f
  • The angular frequency and period are related by: ω = 2π/T

Reference Links

  1. https://www.vaia.com/en-us/explanations/physics/classical-mechanics/angular-frequency-and-period/
  2. https://www.physicsforums.com/threads/the-difference-between-angular-frequency-and-frequency.938722/
  3. https://www.quora.com/What-is-the-difference-between-angular-frequency-and-frequency-with-example

Angular Frequency and Frequency: A Comprehensive Guide for Science Students

by
angular frequency and frequency

Angular frequency and frequency are fundamental concepts in physics that describe the periodic motion of objects. While they are related, they represent distinct quantities that are essential for understanding various phenomena in classical mechanics, electromagnetism, and quantum mechanics.

Understanding Angular Frequency

Angular frequency, denoted by the Greek letter omega (ω), is a measure of the angular displacement of an object per unit time. It represents the rate at which an object completes a full cycle of rotation or oscillation. Angular frequency is measured in radians per second (rad/s) and is calculated using the formula:

ω = 2πf

where f is the frequency of the periodic motion.

The angular frequency of a rotating object can be calculated using the formula:

ω = dθ/dt

where θ is the angular displacement and t is the time.

Examples of Angular Frequency

  1. Circular Motion: Consider a particle moving in a circular path with a constant speed v and radius r. The angular frequency of the particle is given by:

ω = v/r

  1. Simple Harmonic Motion: In a simple harmonic oscillator, such as a mass-spring system or a pendulum, the angular frequency is given by:

ω = √(k/m)

where k is the spring constant or the restoring force constant, and m is the mass of the oscillating object.

  1. Electromagnetic Waves: In the context of electromagnetic waves, the angular frequency is related to the frequency f and the wavelength λ by the equation:

ω = 2πf = 2πc/λ

where c is the speed of light.

Understanding Frequency

angular frequency and frequency

Frequency, denoted by the letter f, is a measure of the number of complete oscillations or rotations of a periodic motion in a given period of time. Frequency is measured in hertz (Hz), which represents the number of cycles per second.

The frequency of a periodic motion can be calculated using the formula:

f = 1/T

where T is the period of the motion, which is the time it takes to complete one full cycle.

Examples of Frequency

  1. Pendulum Clock: The frequency of a pendulum clock is determined by the length of the pendulum and the acceleration due to gravity. The period of a simple pendulum is given by the formula:

T = 2π√(L/g)

where L is the length of the pendulum and g is the acceleration due to gravity. The frequency can then be calculated as f = 1/T.

  1. Alternating Current (AC): In an AC electrical circuit, the frequency represents the number of complete cycles of the voltage or current per second. For example, in the United States, the standard AC frequency is 60 Hz, meaning the voltage and current oscillate 60 times per second.

  2. Radio Waves: Radio waves are a type of electromagnetic radiation, and their frequency is an important characteristic. Radio stations are assigned specific frequency bands, such as AM (amplitude modulation) and FM (frequency modulation), which operate at different frequency ranges.

Relationship between Angular Frequency and Frequency

As mentioned earlier, the relationship between angular frequency and frequency is given by the formula:

ω = 2πf

This formula allows you to convert between angular frequency and frequency, and vice versa. For example, if you know the frequency of a periodic motion, you can calculate the corresponding angular frequency by multiplying the frequency by 2π.

Numerical Examples

  1. Simple Pendulum:
  2. Suppose a simple pendulum has a length L = 1 m and is located on Earth, where the acceleration due to gravity g = 9.8 m/s².
  3. The period of the pendulum can be calculated using the formula T = 2π√(L/g), which gives T ≈ 2.01 s.
  4. The frequency of the pendulum can then be calculated as f = 1/T ≈ 0.497 Hz.

  5. Using the formula ω = 2πf, the angular frequency of the pendulum is ω ≈ 3.14 rad/s.

  6. Electromagnetic Waves:

  7. Consider a radio wave with a frequency of f = 100 MHz (100 million hertz).
  8. To calculate the angular frequency, we use the formula ω = 2πf, which gives ω ≈ 6.28 × 10^8 rad/s.

  9. The wavelength of the radio wave can be calculated using the formula λ = c/f, where c is the speed of light. Assuming c = 3 × 10^8 m/s, the wavelength is λ ≈ 3 m.

  10. Simple Harmonic Motion:

  11. Suppose a mass-spring system has a spring constant k = 50 N/m and a mass m = 2 kg.
  12. The angular frequency of the system can be calculated using the formula ω = √(k/m), which gives ω ≈ 5 rad/s.
  13. The corresponding frequency can be calculated as f = ω/(2π) ≈ 0.796 Hz.

These examples demonstrate the practical applications of angular frequency and frequency in various areas of physics, such as classical mechanics, electromagnetism, and quantum mechanics.

Conclusion

Angular frequency and frequency are fundamental concepts in physics that describe the periodic motion of objects. Angular frequency measures the angular displacement per unit time, while frequency measures the number of complete oscillations or rotations in a given period of time. The relationship between these two quantities is given by the formula ω = 2πf, which allows for the conversion between them.

Understanding the nuances of angular frequency and frequency is crucial for students and researchers in various fields of science, as these concepts are widely used in the analysis and description of a wide range of physical phenomena.

References:

  1. StudySmarter. (n.d.). Angular Frequency & Period: Relationship and Formula. Retrieved from https://www.studysmarter.co.uk/explanations/physics/classical-mechanics/angular-frequency-and-period/
  2. Study.com. (2021, October 11). How to Calculate Angular Frequency Given Standard Frequency. Retrieved from https://study.com/skill/learn/how-to-calculate-angular-frequency-given-standard-frequency-explanation.html
  3. MRI Questions. (n.d.). Angular Frequency (ω) – Questions and Answers ​in MRI. Retrieved from https://www.mriquestions.com/angular-frequency-omega.html
  4. HyperPhysics. (n.d.). Angular Frequency. Retrieved from http://hyperphysics.phy-astr.gsu.edu/hbase/rotq.html
  5. Khan Academy. (n.d.). Frequency and period. Retrieved from https://www.khanacademy.org/science/physics/oscillatory-motion-and-waves/introduction-to-waves/a/frequency-and-period