The half-life formula for radioactivity is a fundamental concept in nuclear physics and chemistry, describing the rate at which radioactive nuclei decay over time. This formula is essential for understanding the behavior of radioactive materials, their applications, and their potential hazards. In this comprehensive guide, we will delve into the intricacies of the half-life formula, its derivation, and its practical applications.
Understanding the Half-Life Formula
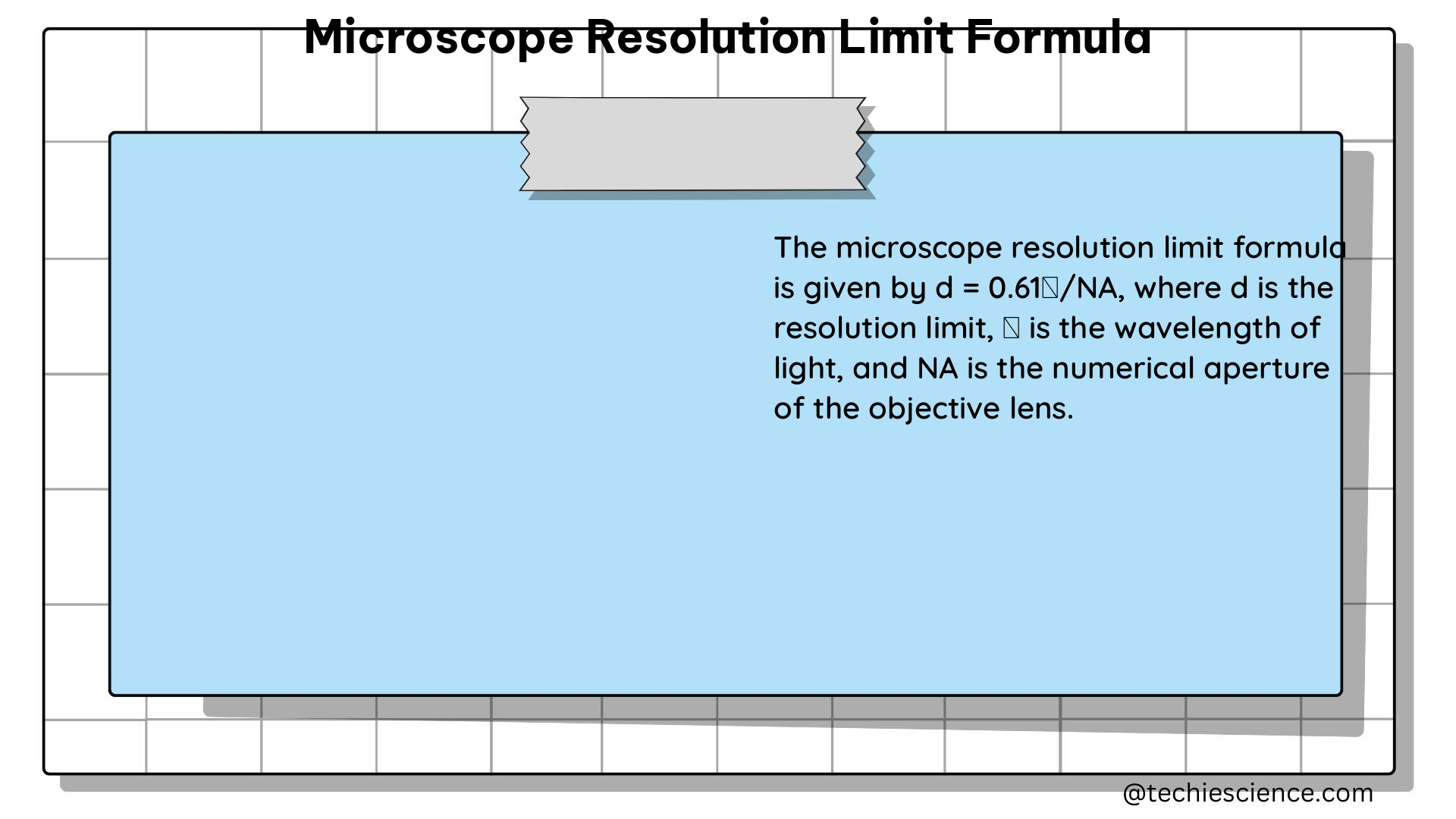
The half-life formula for radioactivity is given by:
t1/2 = ln(2) / λ
where:
– t1/2 is the half-life of the radioactive substance
– λ is the decay constant, which represents the probability of a radioactive nucleus decaying per unit of time
The decay constant, λ, can be calculated using the following formula:
λ = ln(2) / t1/2
The activity, R, of a radioactive substance can be calculated using the formula:
R = (0.693 * N) / t1/2
where N is the number of radioactive nuclei present.
The SI unit for activity is the becquerel (Bq), which is defined as one decay per second.
Derivation of the Half-Life Formula

The half-life formula is derived from the exponential decay law, which describes the rate of radioactive decay. The exponential decay law states that the number of radioactive nuclei, N, decreases exponentially with time, t, according to the equation:
N(t) = N0 * e^(-λt)
where N0 is the initial number of radioactive nuclei.
The half-life, t1/2, is the time it takes for the number of radioactive nuclei to decrease to half of its initial value. This means that:
N(t1/2) = N0 / 2
Substituting this into the exponential decay law, we get:
N0 / 2 = N0 * e^(-λt1/2)
Simplifying this equation, we arrive at the half-life formula:
t1/2 = ln(2) / λ
Examples and Applications
Example 1: Calculating the Half-Life of Carbon-14
Consider a sample of carbon-14 with an activity of 15 Bq. To calculate the half-life of carbon-14, we can use the following steps:
-
Calculate the decay constant,
λ:
λ = ln(2) / t1/2
λ = ln(2) / (5730 y)
λ = 1.21 × 10^-4 y^-1 -
Calculate the half-life,
t1/2:
t1/2 = ln(2) / λ
t1/2 = ln(2) / (1.21 × 10^-4 y^-1)
t1/2 = 5730 y
Therefore, the half-life of carbon-14 is 5730 years.
Example 2: Calculating the Activity of Uranium-238
Consider a sample of uranium-238 with a mass of 1.00 g. To calculate the activity of this sample, we can use the following steps:
-
Calculate the number of radioactive nuclei,
N:
N = 1.00 g / (238 u)
N = 4.20 × 10^21 nuclei -
Calculate the activity,
R:
R = (0.693 * N) / t1/2
R = (0.693 * 4.20 × 10^21 nuclei) / (4.5 × 10^9 y)
R = 1.53 × 10^-11 Bq
Therefore, the activity of a 1.00 g sample of uranium-238 is 1.53 × 10^-11 Bq.
Factors Affecting Half-Life
The half-life of a radioactive substance can be influenced by various factors, including:
-
Nuclear Stability: The stability of the nucleus is a crucial factor in determining the half-life. Unstable nuclei are more likely to undergo radioactive decay, resulting in shorter half-lives.
-
Nuclear Structure: The specific arrangement and composition of the nucleus can also affect the half-life. Certain nuclear configurations may be more or less stable, leading to variations in half-life.
-
Environmental Conditions: External factors, such as temperature, pressure, and the presence of other materials, can sometimes influence the rate of radioactive decay and, consequently, the half-life.
-
Radioactive Decay Modes: The type of radioactive decay (e.g., alpha decay, beta decay, gamma decay) can also affect the half-life, as different decay modes have different probabilities of occurrence.
Limitations and Uncertainties
While the half-life formula provides a reliable way to calculate the decay rate of radioactive substances, there are some limitations and uncertainties to consider:
-
Measurement Uncertainties: The experimental determination of half-life can be subject to various sources of uncertainty, such as measurement errors, statistical fluctuations, and environmental factors.
-
Theoretical Limitations: The half-life formula is based on the assumption of a constant decay rate, which may not always hold true, especially for complex nuclear systems or in the presence of external influences.
-
Quantum Mechanical Effects: At the atomic and subatomic scales, quantum mechanical effects can introduce additional complexities and uncertainties in the behavior of radioactive nuclei.
-
Radioactive Decay Chains: In some cases, radioactive substances undergo a series of decay processes, forming a radioactive decay chain. The half-life formula may need to be modified to account for these more complex scenarios.
Conclusion
The half-life formula is a fundamental tool in the study of radioactivity, providing a quantitative description of the rate of radioactive decay. By understanding the derivation, applications, and limitations of this formula, scientists and researchers can better analyze and predict the behavior of radioactive materials, leading to advancements in fields such as nuclear physics, chemistry, and medical diagnostics.
References
- The uncertainty of the half-life – IOPscience, https://iopscience.iop.org/article/10.1088/0026-1394/52/3/S51
- 5.7: Calculating Half-Life – Chemistry LibreTexts, https://chem.libretexts.org/Courses/Furman_University/CHM101:_Chemistry_and_Global_Awareness_%28Gordon%29/05:_Basics_of_Nuclear_Science/5.07:_Calculating_Half-Life
- How to Calculate the Half-Life of a Decaying Substance – Study.com, https://study.com/skill/learn/how-to-calculate-the-half-life-of-a-decaying-substance-explanation.html
- Half-Life and Activity | Physics – Lumen Learning, https://courses.lumenlearning.com/suny-physics/chapter/31-5-half-life-and-activity/
- 31.5 Half-Life and Activity – College Physics – UCF Pressbooks, https://pressbooks.online.ucf.edu/phy2053bc/chapter/half-life-and-activity/