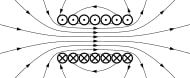
Static electricity is a phenomenon that occurs due to the imbalance of electrical charges on the surface of objects. It is not neutral, as it involves an excess or deficit of electrons on the surface of objects, which can lead to attractive or repulsive forces between objects. The measurement of static electricity is typically done in Coulombs, which is the scientific unit used to express the quantity of electric charge. However, it is not possible to measure the charge in a material directly in Coulombs. Instead, the electric field strength or surface voltage related to the static charge is measured, which is the accepted method of measuring static in industry.
Understanding Electrical Neutrality
According to The Physics Classroom, an electrically neutral object is one that has a balance of protons and electrons, while a charged object has an imbalance of protons and electrons. The quantity of charge on an object involves a counting process, where the total number of electrons and protons are compared to determine the difference between the number of protons and electrons. This difference is then multiplied by 1.6 x 10^-19 Coulombs to determine the overall quantity of charge on the object. The type of charge (positive or negative) is determined by whether the protons or the electrons are in excess.
Electrical Charge and Coulombs
The unit of electrical charge is the Coulomb (C), which is the amount of electric charge carried by a constant current of one ampere flowing for one second. One Coulomb is equivalent to approximately 6.24 x 10^18 electrons. However, it is not possible to measure the charge in a material directly in Coulombs. Instead, the electric field strength or surface voltage related to the static charge is measured, which is the accepted method of measuring static in industry.
Measuring Static Electricity
Fraser Anti-Static Techniques explains that measuring static electricity is important as it allows you to see if there is a static charge present, its size, and where it is being generated. Static electricity is a surplus or deficit of electrons which is measured in Coulombs. However, as it is not possible to measure the charge in a material directly in Coulombs, the electric field strength or surface voltage related to the static charge is measured. This is the accepted method of measuring static in industry.
Factors Affecting Static Electricity

Several factors can affect the generation and accumulation of static electricity, including:
-
Material Composition: The type of material, its surface properties, and the presence of conductive or insulating materials can influence the generation and accumulation of static electricity.
-
Humidity: The level of humidity in the environment can affect the ability of materials to hold or dissipate static charge. Lower humidity environments tend to have higher static electricity levels.
-
Temperature: Changes in temperature can also affect the generation and accumulation of static electricity, as temperature can influence the mobility of electrons and the dielectric properties of materials.
-
Friction and Contact: Rubbing or separating materials can cause the transfer of electrons, leading to the generation of static electricity.
-
Ionization: The presence of ionized air, such as from a corona discharge or radioactive sources, can neutralize static charges by providing a path for the flow of electrons.
Practical Applications of Static Electricity
Static electricity has a wide range of practical applications, including:
-
Electrostatic Printing: Electrostatic printing, such as in laser printers and photocopiers, uses static electricity to attract and transfer toner particles to the printing surface.
-
Electrostatic Painting: Electrostatic painting involves the use of static electricity to attract paint particles to the surface of an object, resulting in a more even and efficient coating.
-
Electrostatic Precipitation: Electrostatic precipitation is used in industrial settings to remove particulate matter from exhaust gases, such as in power plants and cement factories.
-
Electrostatic Discharge (ESD) Protection: Static electricity can be a significant problem in electronics and computer systems, as it can damage sensitive components. ESD protection measures, such as grounding and the use of anti-static materials, are essential in these industries.
-
Electrostatic Separation: Static electricity is used to separate different materials, such as in the recycling of plastics, where static electricity is used to separate different types of plastic.
Conclusion
While it is not possible to measure the charge in a material directly in Coulombs, the electric field strength or surface voltage related to the static charge can be measured, which is the accepted method of measuring static in industry. This allows you to see if there is a static charge present, its size, and where it is being generated. Understanding the nature of static electricity and its measurement is crucial in various industries and applications that rely on the controlled generation, management, and utilization of static electricity.
References:
– The Physics Classroom – Neutral vs. Charged Objects
– The Physics Classroom – Static Electricity Review Answers
– Fraser Anti-Static Techniques – Measurement of Static Electricity