Distance

In the realm of physics, the concepts of displacement and distance are closely intertwined, yet they possess distinct meanings. Displacement refers to the change in an object’s position relative to a fixed reference point, while distance describes the total length of the path traveled by an object, regardless of its direction.

Understanding Displacement and Distance

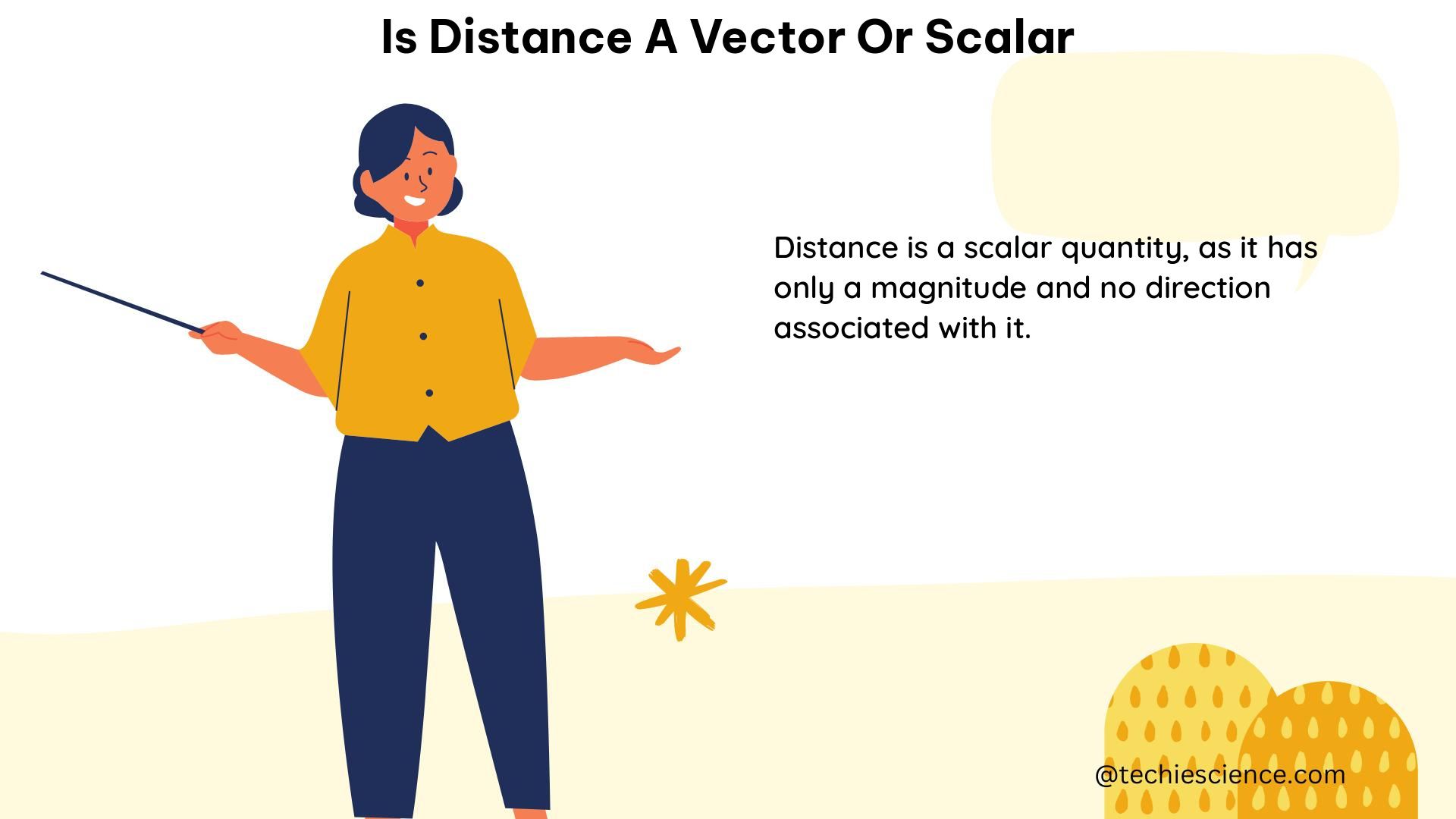
Displacement is a vector quantity, meaning it has both magnitude and direction. On the other hand, distance is a scalar quantity, which only has magnitude. This fundamental difference between the two concepts is the key to understanding why the magnitude of a particle’s displacement can never be greater than the total distance traveled.

Principles of Displacement and Distance

According to the principles of physics, the magnitude of a particle’s displacement can never exceed the total distance traveled. This is because the magnitude of a vector (displacement) cannot be greater than the magnitude of a scalar (distance).

When adding two displacements in the same direction, the magnitude of the resulting displacement will be equal to the sum of the magnitudes of the individual displacements. However, if the displacements are in opposite directions, the magnitude of the resulting displacement will be less than the sum of the magnitudes of the individual displacements.

Examples of Displacement and Distance

Let’s consider an example to illustrate the relationship between displacement and distance. Imagine a cyclist who rides 3 km west and then turns around and rides 2 km east. The displacement of the cyclist is 1 km west, while the total distance traveled is 5 km. The magnitude of the displacement is 1 km, which is less than the total distance traveled.

Displacement and Distance in Motion

To help students understand the difference between distance and displacement, teachers can use examples of motion to illustrate the concepts. For instance, they can walk in a straight line across a room and have students estimate the length of the path. Then, they can walk along a winding path to the same ending point and have students estimate the length of that path. This will help students see that the distance traveled is greater than the displacement when the path is not a straight line.

Displacement and Distance Formulas

The relationship between displacement and distance can be expressed mathematically using the following formulas:

1. Displacement (Δx) = Final position – Initial position
2. Distance (d) = Total length of the path traveled

These formulas highlight the fundamental differences between the two concepts, where displacement is a vector quantity that considers the change in position, while distance is a scalar quantity that measures the total length of the path.

Numerical Examples

To further solidify the understanding of displacement and distance, let’s consider a few numerical examples:

1. A car travels 50 km north and then 30 km south. The displacement is 20 km north, while the total distance traveled is 80 km.
2. A person walks 10 m east, then 5 m west, and finally 8 m east. The displacement is 3 m east, while the total distance traveled is 23 m.
3. A satellite orbits a planet in a circular path with a radius of 1000 km. The displacement of the satellite is 0 km (it returns to its starting point), while the total distance traveled is approximately 6,283 km (2πr).

In all these examples, the magnitude of the displacement is less than the total distance traveled, demonstrating the fundamental principle that the magnitude of a particle’s displacement can never be greater than the total distance traveled.

Conclusion

In summary, while displacement and distance are related concepts in physics, the magnitude of a particle’s displacement can never be greater than the total distance traveled. This is because displacement is a vector quantity, while distance is a scalar quantity, and the principles of physics dictate that the magnitude of a vector cannot be greater than the magnitude of a scalar.

Reference:

1. Relative Motion, Distance, and Displacement
2. Can the magnitude of a particle’s displacement be greater than the distance traveled by the particle?
3. Can displacement ever be greater than distance? If so, how?
4. Can displacement be greater than the distance traveled by an object?
5. Chapter 11 Review

In the realm of physics, the concept of distance being a curve is a fundamental aspect of non-Euclidean geometries, differential geometry, and general relativity. This intriguing idea challenges the traditional notion of distance as a straight line and opens up a world of fascinating mathematical and physical insights.

Understanding Curved Distances

The notion of distance as a curve arises from the study of non-Euclidean geometries, where the traditional Euclidean axioms of parallel lines and the sum of angles in a triangle being 180 degrees do not hold true. In these non-Euclidean spaces, the distance between two points is not necessarily represented by a straight line, but rather by a curve that minimizes the length between them.

One of the key concepts in this context is the geodesic, which is the shortest path between two points in a curved space. In the realm of general relativity, the path of a particle moving under the influence of gravity is a geodesic in spacetime. The length of a geodesic can be calculated using the metric tensor, which describes the geometry of spacetime.

Another important concept is the metric space, where the distance between two points is defined as the length of the shortest path between them, which can be a curve. The length of a curve in a metric space can be calculated using the integral of the norm of its velocity vector with respect to time.

Technical Specifications

Differential Geometry

In differential geometry, the length of a curve is given by the integral of the square root of the dot product of the derivative of the position vector with respect to time and itself. Mathematically, this can be expressed as:

$L = \int_{t_1}^{t_2} \sqrt{\dot{\mathbf{r}}(t) \cdot \dot{\mathbf{r}}(t)} dt$

where $\mathbf{r}(t)$ is the position vector of the curve as a function of time.

General Relativity

In the context of general relativity, the length of a curve in spacetime is given by the integral of the line element, which is a function of the metric tensor and the coordinates of the curve. The line element is expressed as:

$ds^2 = g_{\mu\nu} dx^\mu dx^\nu$

where $g_{\mu\nu}$ is the metric tensor and $dx^\mu$ are the differentials of the coordinates.

Metric Space

In a metric space, the distance between two points $x$ and $y$ is defined as the infimum of the set of lengths of all curves connecting them. Mathematically, this is expressed as:

$d(x, y) = \inf { L(\gamma) : \gamma \text{ is a curve connecting } x \text{ and } y }$

where $L(\gamma)$ is the length of the curve $\gamma$.

Theorems and Formulas

1. Curve Length in Differential Geometry: The length of a curve in differential geometry is given by the formula:
   $L = \int_{t_1}^{t_2} \sqrt{\dot{\mathbf{r}}(t) \cdot \dot{\mathbf{r}}(t)} dt$

2. Line Element in General Relativity: The line element in general relativity is given by the formula:
   $ds^2 = g_{\mu\nu} dx^\mu dx^\nu$

3. Distance in Metric Space: The distance between two points $x$ and $y$ in a metric space is defined as:
   $d(x, y) = \inf { L(\gamma) : \gamma \text{ is a curve connecting } x \text{ and } y }$

Examples and Numerical Problems

Example: Curve Length Calculation

Calculate the length of the curve given by the parametric equations:
$x(t) = t^2$, $y(t) = t^3$, and $z(t) = \sin(t)$ from $t = 0$ to $t = 1$.

Numerical Problem: Curve Fitting and Length Calculation

Given a set of data points in $\mathbb{R}^3$, find the curve of best fit and calculate its length.

Figures and Data Points

Figure: Curve in $\mathbb{R}^3$

A curve in $\mathbb{R}^3$ with its length marked.

Data Points: Object Position

Time (s)	X (m)	Y (m)	Z (m)
0	0	0	0
1	1	2	1
2	4	6	2
3	9	12	3
4	16	20	4

A set of data points in $\mathbb{R}^3$ representing the position of an object at different times.

Values and Measurements

• Value: The length of a curve can be measured in units of length, such as meters or feet.
• Measurement: The length of a curve can be measured using various techniques, such as numerical integration or approximating the curve with straight line segments.

Reference Links

1. Differential Geometry
2. General Relativity
3. Metric Space

Distance and displacement are closely related concepts in physics, but they are not the same. Distance is a scalar quantity that refers to the total length of the path covered by an object during its motion, regardless of the direction. Displacement, on the other hand, is a vector quantity that refers to the change in an object’s position from its initial position to its final position, taking into account both the magnitude and the direction of the change.

Understanding the Difference between Distance and Displacement

To illustrate the difference between distance and displacement, consider the example of a car driving around a circular track. If the car covers a distance of 1 mile during one lap around the track, its displacement after one lap is zero because it ends up at the same point where it started. However, if the car completes two laps around the track, its distance covered is 2 miles, while its displacement is still zero because it ends up at the same point where it started.

The key difference between distance and displacement is that distance is a measure of the total path length covered by an object, while displacement is a measure of the object’s change in position. Distance is a scalar quantity, which means it has only magnitude and no direction, while displacement is a vector quantity, which means it has both magnitude and direction.

Formulas for Distance and Displacement

The formula for distance is simply the total length of the path covered by an object, while the formula for displacement is the difference between the final and initial positions of the object. In mathematical terms, the formula for displacement is:

Δx = xf – xi

where Δx is the displacement, xf is the final position, and xi is the initial position.

Relationship between Distance and Displacement

Despite their differences, distance and displacement are related concepts that are often used together to describe an object’s motion. For example, the average speed of an object can be calculated by dividing the total distance covered by the time it takes to cover that distance, while the average velocity can be calculated by dividing the total displacement by the time it takes to cover that displacement.

Scalar and Vector Quantities

Distance is a scalar quantity, which means it has only magnitude and no direction. In contrast, displacement is a vector quantity, which means it has both magnitude and direction.

Scalar quantities are represented by a single number, such as the distance traveled or the mass of an object. Vector quantities, on the other hand, are represented by both a magnitude and a direction, such as the displacement of an object or the velocity of an object.

Examples of Distance and Displacement

1. Example 1: A car driving around a circular track
2. Distance covered: 1 mile per lap

3. Displacement: 0 (the car ends up at the same point where it started)

4. Example 2: A person walking from their house to the park and back

5. Distance covered: the total length of the path walked, including the return trip

6. Displacement: the difference between the final and initial positions (the distance between the house and the park)

7. Example 3: A ball thrown straight up in the air

8. Distance covered: the total length of the path traveled by the ball, including the upward and downward motion
9. Displacement: the difference between the final and initial positions (the height reached by the ball)

Numerical Problems

1. Problem 1: A person walks 5 km north, then 3 km east, and finally 2 km south. Calculate the distance traveled and the displacement.
2. Distance traveled = 5 km + 3 km + 2 km = 10 km

3. Displacement = √((5 km)^2 + (-2 km)^2) = √(25 + 4) = √29 km

4. Problem 2: A car travels 20 km east, then 10 km north, and finally 15 km west. Calculate the distance traveled and the displacement.

5. Distance traveled = 20 km + 10 km + 15 km = 45 km
6. Displacement = √((20 km)^2 + (10 km)^2 + (-15 km)^2) = √(400 + 100 + 225) = √725 km

Conclusion

In summary, distance and displacement are not the same, but they are closely related concepts in physics that are used to describe an object’s motion. Distance is a scalar quantity that refers to the total length of the path covered by an object, while displacement is a vector quantity that refers to the change in an object’s position from its initial position to its final position. The formula for distance is the total length of the path covered, while the formula for displacement is the difference between the final and initial positions. Despite their differences, distance and displacement are often used together to describe an object’s motion.

References:

• “Distance and Displacement – Definition, Formulas, and Examples” – GeeksforGeeks
• “Distance and Displacement review (article)” – Khan Academy
• “2.1 Relative Motion, Distance, and Displacement” – Physics OpenStax
• “Distance versus Displacement” – The Physics Classroom
• “Difference between Distance and Displacement” – DifferenceBetween.net

Distance is a fundamental concept in physics, and it is often used in conjunction with other variables such as time, velocity, and acceleration to describe the motion of objects. While distance is generally considered a positive quantity, there are certain contexts where negative values may be used to represent reverse travel or displacement in the negative direction.

Understanding Distance as a Scalar Quantity

Distance is a scalar quantity, which means it has only magnitude and no direction. This is in contrast to vector quantities, such as displacement, velocity, and acceleration, which have both magnitude and direction. As a scalar quantity, distance is always positive and cannot be negative.

The formula for calculating distance is:

d = |x2 - x1|

where d represents the distance, x2 is the final position, and x1 is the initial position. The absolute value function |x2 - x1| ensures that the distance is always positive, regardless of the direction of motion.

Negative Values in Displacement and Velocity

While distance itself is always positive, the related quantities of displacement and velocity can have negative values. Displacement is a vector quantity that represents the change in position of an object, and it can be positive or negative depending on the direction of motion.

The formula for calculating displacement is:

Δx = x2 - x1

where Δx represents the displacement, x2 is the final position, and x1 is the initial position. If the object moves in the positive direction, the displacement will be positive. If the object moves in the negative direction, the displacement will be negative.

Similarly, velocity is a vector quantity that represents the rate of change of an object’s position. Velocity can be positive or negative, depending on the direction of motion. The formula for calculating velocity is:

v = Δx / Δt

where v represents the velocity, Δx is the displacement, and Δt is the change in time.

Negative Values in Physics Experiments and Data Analysis

In physics experiments and data analysis, negative values may be used to represent reverse travel or displacement in the negative direction. This is done to accurately represent the data and maintain consistency in the measurement of position and velocity.

For example, consider an object moving back and forth along a straight line. If the object starts at a position of 0 meters, moves to a position of 5 meters, and then moves back to a position of -3 meters, the displacement would be:

Δx = -3 meters

The negative value of the displacement indicates that the object has moved in the negative direction.

Similarly, if an object is moving in the negative direction with a negative velocity, the velocity would be represented as a negative value. This allows for a more accurate representation of the object’s motion and facilitates the calculation of other quantities, such as acceleration.

Interpreting Negative Values in Physics

When encountering negative values in physics, it is important to understand the context and meaning of these values. Negative values do not necessarily indicate an error or a problem with the measurement; rather, they represent the direction of motion or displacement.

It is crucial to interpret negative values correctly to ensure meaningful analysis and interpretation of the data. For example, a negative displacement may indicate that an object has moved in the opposite direction, while a negative velocity may indicate that the object is moving in the opposite direction.

Examples and Numerical Problems

1. Example 1: An object starts at a position of 2 meters and moves to a position of -4 meters. Calculate the distance and displacement.

2. Distance: d = |x2 - x1| = |-4 - 2| = 6 meters

3. Displacement: Δx = x2 - x1 = -4 - 2 = -6 meters

4. Example 2: An object starts at a position of 0 meters, moves to a position of 10 meters, and then moves back to a position of -5 meters. Calculate the total distance and displacement.

5. Total distance: d = |x2 - x1| + |x3 - x2| = |10 - 0| + |-5 - 10| = 10 + 15 = 25 meters

6. Displacement: Δx = x3 - x1 = -5 - 0 = -5 meters

7. Numerical Problem 1: An object starts at a position of 3 meters, moves to a position of -7 meters, and then moves to a position of 5 meters. Calculate the total distance and displacement.

8. Total distance: d = |x2 - x1| + |x3 - x2| = |-7 - 3| + |5 - (-7)| = 10 + 12 = 22 meters

9. Displacement: Δx = x3 - x1 = 5 - 3 = 2 meters

10. Numerical Problem 2: An object starts at a position of -2 meters, moves to a position of 8 meters, and then moves to a position of -4 meters. Calculate the total distance and displacement.

11. Total distance: d = |x2 - x1| + |x3 - x2| = |8 - (-2)| + |-4 - 8| = 10 + 12 = 22 meters

12. Displacement: Δx = x3 - x1 = -4 - (-2) = -2 meters

These examples and numerical problems demonstrate how distance is always positive, while displacement and other vector quantities can have negative values to represent reverse travel or displacement in the negative direction.

Conclusion

In summary, while distance is a scalar quantity that is always positive, there are situations in physics where negative values may be used to represent reverse travel or displacement in the negative direction. Understanding the context and meaning of these negative values is crucial for accurate analysis and interpretation of data in physics experiments and calculations.

References:

1. CrossFit’s Measure of Intensity is Power Kinematics
2. University Physics – Lumen Learning
3. Very basic question regarding distance : r/AskPhysics – Reddit
4. Make Measurable: What Galileo Didn’t Say about the Subjectivity of Algorithms
5. Positive vs. Normative Economics: What’s the Difference?