Difference

Difference between Moment of Inertia and Momentum

Definition of Moment of Inertia

When it comes to understanding rotational motion, two important concepts that often get confused are moment of inertia and momentum. Let’s start by defining moment of inertia.

Moment of inertia, denoted by the symbol “I,” is a property of an object that describes its resistance to changes in rotational motion. It quantifies how the mass of an object is distributed around its axis of rotation. In simpler terms, it measures how difficult it is to change the rotational motion of an object.

To calculate the moment of inertia, we need to consider both the mass of the object and how that mass is distributed relative to the axis of rotation. Objects with a larger moment of inertia require more torque (rotational force) to produce the same angular acceleration compared to objects with a smaller moment of inertia.

Definition of Momentum

Now, let’s move on to momentum. Momentum is a fundamental concept in physics that describes the motion of an object. It is defined as the product of an object’s mass and its velocity. Momentum is a vector quantity, meaning it has both magnitude and direction.

The momentum of an object can be calculated using the formula:

where “p” represents momentum, “m” represents mass, and “v” represents velocity.

Momentum is conserved in a closed system, meaning that the total momentum before an event or interaction is equal to the total momentum after the event or interaction. This principle is known as the law of conservation of momentum.

Comparison of Moment of Inertia and Momentum

Now that we have defined both moment of inertia and momentum, let’s compare the two concepts.

1. Definition: Moment of inertia measures an object’s resistance to changes in rotational motion, while momentum describes the motion of an object in linear motion.

2. Calculation: Moment of inertia depends on the mass distribution of an object around its axis of rotation, while momentum depends on the mass and velocity of an object.

3. Units: Moment of inertia is measured in units of kilogram square meters (kg·m²), while momentum is measured in units of kilogram meters per second (kg·m/s).

4. Conservation: Moment of inertia is not conserved in a system, whereas momentum is conserved in a closed system.

5. Application: Moment of inertia is commonly used in rotational mechanics to analyze the behavior of rotating objects, such as wheels, gears, and flywheels. On the other hand, momentum is used to analyze the motion of objects in linear motion, such as collisions and projectile motion.

In summary, moment of inertia and momentum are two distinct concepts in physics. Moment of inertia relates to rotational motion and describes an object’s resistance to changes in rotational motion. Momentum, on the other hand, relates to linear motion and describes an object’s motion in terms of its mass and velocity. While both concepts are important in understanding the behavior of objects, they have different applications and calculations.

Difference between Torque and Bending Moment

Definition of Torque

Torque is a term commonly used in physics and engineering to describe a rotational force. It is a measure of the tendency of a force to cause an object to rotate about an axis. In simpler terms, torque can be thought of as a twisting or turning force. It is denoted by the symbol “τ” and is measured in units of Newton-meters (Nm) or foot-pounds (ft-lb).

Definition of Bending Moment

Bending moment, on the other hand, is a term used in structural engineering to describe the internal forces that act on a beam or any other structural element when subjected to external loads. It is a measure of the bending or flexural stress experienced by the material. Bending moment is denoted by the symbol “M” and is measured in units of Newton-meters (Nm) or foot-pounds (ft-lb).

Comparison of Torque and Bending Moment

While both torque and bending moment involve rotational forces, they are used in different contexts and have distinct applications. Let’s take a closer look at the key differences between the two:

1. Definition: Torque is a measure of the rotational force applied to an object, while bending moment is a measure of the internal forces experienced by a structural element when subjected to external loads.

2. Application: Torque is primarily used in the study of rotational motion, such as in the analysis of rotating machinery or the calculation of angular acceleration. Bending moment, on the other hand, is used in the design and analysis of structures, such as beams, columns, and bridges.

3. Axis of Rotation: Torque is associated with a specific axis of rotation, which is the point around which an object rotates. Bending moment, on the other hand, is associated with the neutral axis of a structural element, which is the line that experiences no deformation when subjected to bending.

4. Magnitude: The magnitude of torque depends on the force applied and the distance from the axis of rotation. In contrast, the magnitude of bending moment depends on the applied load and the distance from the neutral axis.

5. Effects: Torque causes an object to rotate or change its rotational speed. Bending moment, on the other hand, causes a structural element to deform or bend.

To summarize, torque and bending moment are both important concepts in the fields of physics and engineering, but they have different definitions, applications, and effects. Torque is associated with rotational motion, while bending moment is associated with the internal forces experienced by structural elements. Understanding the difference between these two concepts is crucial for engineers and physicists working in the respective fields.

Difference between Angular Momentum and Torque

Definition of Angular Momentum

Angular momentum is a fundamental concept in physics that describes the rotational motion of an object. It is a vector quantity that depends on both the mass and the distribution of mass within the object, as well as its rotational speed. Angular momentum is denoted by the symbol L and is defined as the product of the moment of inertia (I) and the angular velocity (ω) of the object.

In simpler terms, angular momentum is a measure of how fast an object is rotating and how much mass is distributed away from its axis of rotation. It is similar to linear momentum, which describes the motion of an object in a straight line, but angular momentum specifically applies to rotational motion.

Definition of Torque

Torque, on the other hand, is a measure of the rotational force applied to an object. It is a vector quantity that depends on the magnitude of the force applied and the distance from the axis of rotation at which the force is applied. Torque is denoted by the symbol τ and is defined as the product of the force (F) and the perpendicular distance (r) from the axis of rotation to the line of action of the force.

In simpler terms, torque can be thought of as a twisting or turning force that causes an object to rotate. It is similar to force in linear motion, but torque specifically applies to rotational motion.

Comparison of Angular Momentum and Torque

While both angular momentum and torque are related to rotational motion, they have distinct differences in their definitions and applications.

1. Definition: Angular momentum is a measure of the rotational motion of an object, taking into account its mass distribution and rotational speed. Torque, on the other hand, is a measure of the rotational force applied to an object.

2. Quantities: Angular momentum is a vector quantity, meaning it has both magnitude and direction. It depends on the moment of inertia and angular velocity of the object. Torque is also a vector quantity, depending on the magnitude and direction of the force applied and the distance from the axis of rotation.

3. Units: Angular momentum is measured in units of kilogram meters squared per second (kg·m²/s), while torque is measured in units of newton meters (N·m).

4. Conservation: Angular momentum is conserved in a closed system when no external torques act on the system. This is known as the conservation of angular momentum. Torque, on the other hand, is not conserved and can change the rotational motion of an object.

5. Applications: Angular momentum is used to describe the motion of rotating objects, such as planets, spinning tops, and rotating wheels. Torque is used to explain the rotational equilibrium of objects, the motion of gears, and the operation of machines.

In summary, angular momentum and torque are related concepts in rotational motion, but they have distinct definitions and applications. Angular momentum describes the rotational motion of an object, while torque represents the rotational force applied to an object. Understanding these concepts is essential in the study of rotational dynamics and mechanics.

Difference between Moment of Inertia and Torque

Definition of Moment of Inertia

When we talk about rotational motion, we often come across the terms “moment of inertia” and “torque.” These concepts play a crucial role in understanding the dynamics of rotating objects. Let’s start by defining the moment of inertia.

The moment of inertia, denoted by the symbol “I,” is a measure of an object’s resistance to changes in its rotational motion. It quantifies how mass is distributed around an axis of rotation. In simpler terms, it tells us how difficult it is to start or stop the rotation of an object.

To calculate the moment of inertia, we need to consider both the mass of the object and its distribution. Objects with more mass concentrated farther from the axis of rotation have a higher moment of inertia. On the other hand, objects with mass distributed closer to the axis have a lower moment of inertia.

Definition of Torque

Now, let’s move on to the definition of torque. Torque is the rotational equivalent of force. It is the measure of the force’s effectiveness in causing an object to rotate about an axis. In other words, torque is the twisting or turning force that causes an object to change its rotational motion.

Torque is denoted by the symbol “τ” and is calculated by multiplying the force applied to an object by the distance from the axis of rotation. The formula for torque is:

τ = F * r

Where:
– τ is the torque
– F is the force applied
– r is the distance from the axis of rotation

Comparison of Moment of Inertia and Torque

While both moment of inertia and torque are related to rotational motion, they have different roles and applications.

• Role: The moment of inertia determines how difficult it is to change the rotational motion of an object, while torque determines the rate at which the rotational motion changes.

• Measurement: The moment of inertia is a property of the object itself and depends on its mass distribution. Torque, on the other hand, is a measure of the force applied and the distance from the axis of rotation.

• Units: The moment of inertia is measured in units of kilogram square meters (kg·m²), while torque is measured in units of newton meters (N·m).

• Effect on Motion: The moment of inertia affects the object’s ability to resist changes in its rotational motion. A higher moment of inertia means it is more difficult to change the object’s rotational speed. Torque, on the other hand, directly affects the rate at which the object’s rotational speed changes. A larger torque will cause the object to rotate faster.

• Applications: Moment of inertia is used in various areas of physics and engineering, such as calculating the rotational kinetic energy and angular momentum of objects. Torque, on the other hand, is commonly used in mechanical systems, such as engines, motors, and levers, to produce or control rotational motion.

In summary, the moment of inertia and torque are both important concepts in rotational mechanics. The moment of inertia describes an object’s resistance to changes in its rotational motion, while torque represents the twisting force that causes an object to rotate. Understanding these concepts is essential for analyzing and predicting the behavior of rotating objects.

Differences between Moment and Bending Moment

Definition of Moment

In physics, the term “moment” refers to the turning effect produced by a force acting on an object. It is a measure of the rotational force or torque applied to an object. Moment is calculated by multiplying the magnitude of the force by the perpendicular distance from the point of rotation to the line of action of the force. It is denoted by the symbol “M” and is measured in units of newton-meters (Nm) or pound-feet (lb-ft).

Definition of Bending Moment

On the other hand, the term “bending moment” specifically relates to the bending or flexing of a structural element, such as a beam or a column. It is a measure of the internal forces within the structure that cause it to bend. Bending moment is calculated by multiplying the magnitude of the force applied perpendicular to the structure by the perpendicular distance from the point of rotation to the line of action of the force. It is denoted by the symbol “M” and is also measured in units of newton-meters (Nm) or pound-feet (lb-ft).

Comparison of Moment and Bending Moment

While both moment and bending moment involve the concept of rotational force, they differ in their applications and calculations.

1. Application: Moment is a general term used to describe the rotational force acting on any object, whereas bending moment specifically refers to the internal forces within a structural element that cause it to bend.

2. Calculation: Moment is calculated by multiplying the force magnitude by the perpendicular distance from the point of rotation to the line of action of the force. Bending moment, on the other hand, is calculated by multiplying the force magnitude by the perpendicular distance from the point of rotation to the line of action of the force, but only for forces that cause bending within a structure.

3. Sign Convention: In moment calculations, a positive sign indicates a counterclockwise rotation, while a negative sign indicates a clockwise rotation. In bending moment calculations, the sign convention depends on the type of bending being considered. For example, in a simply supported beam, a positive bending moment indicates sagging (concave upwards), while a negative bending moment indicates hogging (concave downwards).

4. Effects: Moment affects the rotational equilibrium and dynamics of an object, whereas bending moment affects the structural integrity and stability of a beam or column. Understanding the bending moment within a structure is crucial for designing safe and efficient structures.

To summarize, moment is a general term used to describe rotational forces, while bending moment specifically relates to the internal forces causing bending within a structure. Both concepts involve the calculation of forces and distances, but they have different applications and effects.

Difference between Moment Arm and Torque

Definition of Moment Arm

In the realm of rotational mechanics, the concept of a moment arm plays a crucial role. Also known as the lever arm, the moment arm refers to the perpendicular distance between the axis of rotation and the line of action of a force. It is denoted by the symbol ‘r’ and is measured in units of length, such as meters or feet.

The moment arm determines the effectiveness of a force in producing rotational motion or torque. It is an essential parameter in understanding the dynamics of rotational systems. The longer the moment arm, the greater the leverage and the more significant the effect of the force on the rotation.

Definition of Torque

Torque, on the other hand, is the rotational equivalent of force. It is a measure of the tendency of a force to cause an object to rotate about an axis. Torque is denoted by the symbol ‘τ’ and is measured in units of force multiplied by distance, such as newton-meters or foot-pounds.

Torque is calculated by multiplying the magnitude of the force applied perpendicular to the moment arm by the length of the moment arm. It represents the rotational force that causes an object to change its angular motion or maintain rotational equilibrium.

Comparison of Moment Arm and Torque

While the moment arm and torque are closely related, they are distinct concepts in rotational mechanics. Here are the key differences between moment arm and torque:

1. Definition: The moment arm refers to the perpendicular distance between the axis of rotation and the line of action of a force, while torque is the rotational force that causes an object to change its angular motion or maintain rotational equilibrium.

2. Symbol: The moment arm is represented by the symbol ‘r’, whereas torque is denoted by the symbol ‘τ’.

3. Units: The moment arm is measured in units of length, such as meters or feet, while torque is measured in units of force multiplied by distance, such as newton-meters or foot-pounds.

4. Calculation: The moment arm is a physical distance that remains constant, whereas torque is calculated by multiplying the magnitude of the force applied perpendicular to the moment arm by the length of the moment arm.

5. Effect: The moment arm determines the effectiveness of a force in producing rotational motion, while torque represents the rotational force that causes an object to change its angular motion or maintain rotational equilibrium.

In summary, the moment arm and torque are interrelated concepts in rotational mechanics. The moment arm determines the leverage of a force, while torque represents the rotational force that causes an object to rotate. Understanding the difference between these two concepts is essential for comprehending the dynamics of rotational systems.

Difference between Moment Couple and Torque

Definition of Moment Couple

In physics, a moment couple refers to a pair of equal and opposite forces that act on a body, but not along the same line. This creates a turning effect, also known as a moment, around a specific point or axis. The moment couple is characterized by two parallel forces with the same magnitude and opposite directions, but they are separated by a distance called the arm. The arm is the perpendicular distance between the line of action of the forces.

Definition of Torque

On the other hand, torque is a term commonly used in mechanics to describe the rotational effect of a force. It is a measure of the force’s ability to cause an object to rotate around an axis or pivot point. Torque is a vector quantity, meaning it has both magnitude and direction. It is calculated by multiplying the magnitude of the force by the perpendicular distance from the axis of rotation to the line of action of the force.

Comparison of Moment Couple and Torque

While both moment couple and torque involve rotational effects, there are some key differences between the two:

1. Nature of Forces: In a moment couple, the forces are equal in magnitude, opposite in direction, and act along parallel lines. On the other hand, torque is the product of a force and its perpendicular distance from the axis of rotation.

2. Direction of Rotation: A moment couple produces a pure rotation without any translation. It only causes the body to rotate around the axis. In contrast, torque can cause both rotation and translation of an object.

3. Application: Moment couples are commonly used in structural engineering and mechanics to analyze the stability and equilibrium of structures. They are often used to determine the effects of external loads on buildings, bridges, and other structures. Torque, on the other hand, is frequently used in the study of rotational motion, such as the motion of gears, wheels, and other rotating objects.

4. Units of Measurement: Moment couple is measured in newton-meters (N·m), while torque is also measured in newton-meters (N·m). The units are the same because both moment couple and torque represent the rotational effect of a force.

To summarize, moment couple and torque are related concepts that describe the rotational effects of forces. While moment couple refers specifically to a pair of equal and opposite forces acting on a body, torque is a more general term that describes the rotational effect of any force. Understanding the difference between these terms is crucial in the study of rotational mechanics and dynamics.
Difference between Moments and Torque

Definition of Moments

In physics, the term “moment” refers to the turning effect produced by a force around a point or axis. Moments are commonly associated with rotational motion and are used to describe the tendency of an object to rotate. They play a crucial role in understanding rotational equilibrium, dynamics, and mechanics.

A moment is calculated by multiplying the magnitude of the force by the perpendicular distance from the point or axis of rotation. Mathematically, it can be expressed as:

Moment = Force × Perpendicular Distance

Moments are vector quantities, meaning they have both magnitude and direction. The direction of a moment is determined by the right-hand rule, where the thumb points in the direction of the force and the fingers curl in the direction of the moment.

Definition of Torque

Torque, on the other hand, is a term commonly used in engineering and mechanics to describe the rotational force acting on an object. It is a measure of how effectively a force can cause an object to rotate about a specific axis. Torque is also known as the moment of force.

Torque is calculated by multiplying the magnitude of the force by the perpendicular distance from the axis of rotation. Mathematically, it can be expressed as:

Torque = Force × Perpendicular Distance

Similar to moments, torque is also a vector quantity and has both magnitude and direction. The direction of torque is determined by the right-hand rule, where the thumb points in the direction of the force and the fingers curl in the direction of the torque.

Comparison of Moments and Torque

While moments and torque are related concepts, there are some key differences between them. Let’s explore these differences:

1. Definition: Moments are defined as the turning effect produced by a force around a point or axis, whereas torque is defined as the rotational force acting on an object.

2. Usage: Moments are commonly used in physics to describe rotational motion, equilibrium, and dynamics. Torque, on the other hand, is primarily used in engineering and mechanics to analyze the effectiveness of a force in causing rotation.

3. Calculation: Both moments and torque are calculated by multiplying the magnitude of the force by the perpendicular distance from the point or axis of rotation. The main difference lies in their applications and the specific contexts in which they are used.

4. Direction: Moments and torque are both vector quantities and have direction associated with them. The direction of a moment or torque is determined by the right-hand rule, which helps establish the orientation of the rotational force.

5. Units: Moments and torque are measured in different units. Moments are typically measured in newton-meters (Nm), while torque is measured in the same unit, newton-meters (Nm), or foot-pounds (ft-lb) in some cases.

In summary, moments and torque are related concepts that describe the rotational effects of forces. Moments are more commonly used in physics, while torque finds its applications in engineering and mechanics. While they share similarities in their calculation and direction, the specific contexts in which they are used and their units of measurement set them apart. Understanding the difference between moments and torque is essential for comprehending rotational motion and its applications in various fields.

Difference between Moment of Inertia and Torque

Definition of Moment of Inertia

When it comes to understanding the behavior of rotating objects, the concept of moment of inertia plays a crucial role. Moment of inertia, denoted by the symbol I, is a measure of an object’s resistance to changes in its rotational motion. It quantifies how mass is distributed around an axis of rotation. In simpler terms, it tells us how difficult it is to change the rotational motion of an object.

To calculate the moment of inertia, we need to consider both the mass and the distribution of that mass relative to the axis of rotation. The formula for moment of inertia depends on the shape and mass distribution of the object. For example, the moment of inertia of a solid cylinder is given by the formula I = (1/2) * m * r^2, where m is the mass of the cylinder and r is its radius.

Definition of Torque

Torque, on the other hand, is a measure of the rotational force applied to an object. It is the product of the force applied and the perpendicular distance from the axis of rotation to the line of action of the force. Torque is denoted by the symbol τ and is measured in units of Newton-meters (N·m).

In simpler terms, torque can be thought of as a twisting force that causes an object to rotate around an axis. It is the rotational counterpart of linear force. Just as force can cause linear motion, torque can cause rotational motion.

Comparison of Moment of Inertia and Torque

While both moment of inertia and torque are related to rotational motion, they represent different aspects of it. Let’s take a closer look at the key differences between these two concepts:

1. Definition: Moment of inertia is a measure of an object’s resistance to changes in its rotational motion, based on its mass distribution. Torque, on the other hand, is a measure of the rotational force applied to an object.

2. Symbol: Moment of inertia is denoted by the symbol I, while torque is denoted by the symbol τ.

3. Units: Moment of inertia is measured in units of kilogram square meters (kg·m^2), while torque is measured in units of Newton-meters (N·m).

4. Calculation: Moment of inertia depends on the mass and distribution of mass relative to the axis of rotation. It requires knowledge of the object’s shape and mass distribution. Torque, on the other hand, depends on the force applied and the perpendicular distance from the axis of rotation to the line of action of the force.

5. Effect on Motion: Moment of inertia affects how an object responds to changes in its rotational motion. Objects with larger moment of inertia are more resistant to changes in their rotational motion. Torque, on the other hand, causes objects to rotate or change their rotational motion.

In summary, moment of inertia and torque are both important concepts in rotational mechanics. Moment of inertia quantifies an object’s resistance to changes in its rotational motion, while torque represents the rotational force applied to an object. Understanding these concepts helps us analyze and predict the behavior of rotating objects in various situations.

Why is Torque Called Moment

Explanation of the Term “Moment”

In the realm of physics, the term “moment” is often used to describe a turning effect or rotational force. It is closely related to the concept of torque, which is the measure of the force that causes an object to rotate around an axis. The term “moment” is derived from the Latin word “momentum,” meaning movement or motion.

When we talk about a moment in physics, we are referring to the rotational effect produced by a force acting on an object. This effect depends not only on the magnitude of the force but also on the distance between the point of application of the force and the axis of rotation. In other words, the moment is a measure of how much a force can cause an object to rotate.

Relationship between Torque and Moment

Torque and moment are often used interchangeably, especially in the context of rotational dynamics. While they are closely related, there is a subtle difference between the two.

Torque specifically refers to the twisting or turning force that causes an object to rotate. It is a vector quantity, meaning it has both magnitude and direction. In simple terms, torque can be thought of as the rotational equivalent of force in linear motion.

On the other hand, moment is a more general term that encompasses both torque and other rotational effects. It can refer to the rotational force produced by a single force acting on an object, as well as the overall rotational effect caused by multiple forces acting on different points of an object.

To put it simply, torque is a specific type of moment that deals with the twisting force, while moment is a broader term that encompasses various rotational effects.

To better understand the relationship between torque and moment, let’s consider an example. Imagine a seesaw with a person sitting on one end. When the person pushes down on their side, they exert a force that causes the seesaw to rotate around a pivot point. This force is the torque, and the resulting rotational effect is the moment.

In summary, torque and moment are closely related terms used to describe rotational forces and effects. Torque specifically refers to the twisting force that causes rotation, while moment is a broader term that encompasses various rotational effects. Understanding these concepts is crucial in the study of rotational mechanics and dynamics.

Difference between Moment and Bending Moment

Definition of Moment

In physics, the term “moment” refers to the turning effect produced by a force around a point or axis. It is a measure of the rotational force or torque applied to an object. The moment of a force is calculated by multiplying the magnitude of the force by the perpendicular distance from the point of rotation to the line of action of the force. The SI unit for moment is the Newton-meter (Nm).

Definition of Bending Moment

On the other hand, the bending moment is a specific type of moment that occurs in structural mechanics. It is the measure of the internal bending forces within a beam or any other structural element. When a beam is subjected to external loads, such as weight or applied forces, it experiences bending moments that cause it to bend or deform. The bending moment at any point along the beam is calculated by multiplying the magnitude of the force acting on the beam by the perpendicular distance from that point to the line of action of the force. The unit for bending moment is also the Newton-meter (Nm).

Comparison of Moment and Bending Moment

While both moment and bending moment involve the concept of rotational force, they differ in their applications and calculations.

1. Definition: Moment is a general term used to describe the rotational force around a point or axis, whereas bending moment specifically refers to the internal forces within a beam or structural element.

2. Calculation: The calculation of moment involves multiplying the force magnitude by the perpendicular distance to the line of action of the force. In contrast, the calculation of bending moment involves multiplying the force magnitude by the perpendicular distance to the point of interest along the beam.

3. Application: Moments are commonly used in various areas of physics, engineering, and mechanics to analyze rotational motion, equilibrium, and dynamics. Bending moments, on the other hand, are primarily used in structural analysis to determine the strength and stability of beams and other load-bearing structures.

4. Effects: Moments can cause an object to rotate or change its rotational motion. Bending moments, however, cause beams to bend or deform, leading to structural deflection or failure if the bending stresses exceed the beam’s capacity.

To summarize, while both moment and bending moment involve rotational forces, they differ in their definitions, calculations, applications, and effects. Moments have a broader scope and are used in various fields, while bending moments specifically pertain to the internal forces within beams and other structural elements. Understanding the distinction between these terms is crucial for engineers, physicists, and anyone involved in the analysis and design of structures.

Difference between Magnetic Dipole Moment and Torque

Definition of Magnetic Dipole Moment

The magnetic dipole moment is a fundamental concept in physics that describes the magnetic properties of an object. It is a vector quantity that represents the strength and orientation of a magnetic dipole. A magnetic dipole is formed when a current-carrying loop or a magnetized object generates a magnetic field. The magnitude of the magnetic dipole moment is given by the product of the current flowing through the loop and the area enclosed by the loop. The direction of the magnetic dipole moment is perpendicular to the plane of the loop, following the right-hand rule.

Definition of Torque

Torque, on the other hand, is a rotational force that causes an object to rotate around an axis. It is a vector quantity that depends on the magnitude of the force applied and the distance between the axis of rotation and the point where the force is applied. Torque is also known as the moment of force. It is measured in units of Newton-meters (N·m) or foot-pounds (ft·lb).

Comparison of Magnetic Dipole Moment and Torque

While both magnetic dipole moment and torque are related to rotational motion, they have distinct differences in their definitions and applications.

1. Nature of Quantity: The magnetic dipole moment is a property of an object that describes its magnetic behavior, whereas torque is a force that causes rotational motion.

2. Physical Representation: The magnetic dipole moment is represented by a vector quantity, indicating both magnitude and direction. Torque, on the other hand, is also a vector quantity but is represented by a cross product of the force vector and the displacement vector.

3. Units: The magnetic dipole moment is measured in units of Ampere-square meters (A·m²), while torque is measured in units of Newton-meters (N·m) or foot-pounds (ft·lb).

4. Application: The magnetic dipole moment is commonly used to describe the behavior of magnets, magnetic materials, and current-carrying loops in the presence of a magnetic field. It is crucial in understanding phenomena such as magnetism, electromagnetism, and magnetic interactions. Torque, on the other hand, is used to analyze rotational motion and equilibrium in mechanical systems. It is essential in areas such as mechanics, engineering, and physics.

In summary, the magnetic dipole moment is a property that describes the magnetic behavior of an object, while torque is a force that causes rotational motion. Both concepts have distinct definitions and applications, with the magnetic dipole moment being more focused on magnetism and the torque being more relevant to rotational mechanics. Understanding these differences helps in comprehending the underlying principles of magnetism and rotational dynamics.

Distinguish between Moment and Momentum

Definition of Moment

In physics, the term “moment” refers to the turning effect or rotational force that is applied to an object. It is a crucial concept in the study of rotational motion and equilibrium. The moment of an object is calculated by multiplying the force applied to it by the perpendicular distance from the point of rotation, also known as the pivot or fulcrum. The SI unit for moment is the Newton-meter (N·m).

Definition of Momentum

On the other hand, momentum is a fundamental concept in classical mechanics that describes the motion of an object. It is defined as the product of an object’s mass and its velocity. Momentum is a vector quantity, meaning it has both magnitude and direction. The SI unit for momentum is kilogram-meter per second (kg·m/s).

Comparison of Moment and Momentum

Although the terms “moment” and “momentum” sound similar, they have distinct meanings and applications in physics. Let’s explore the key differences between these two concepts:

1. Definition: Moment is a measure of the rotational force applied to an object, while momentum is a measure of the object’s motion.

2. Calculation: Moment is calculated by multiplying the force applied to an object by the perpendicular distance from the point of rotation. On the other hand, momentum is calculated by multiplying an object’s mass by its velocity.

3. Units: Moment is measured in Newton-meters (N·m), while momentum is measured in kilogram-meter per second (kg·m/s).

4. Type of Quantity: Moment is a scalar quantity, meaning it only has magnitude. Momentum, on the other hand, is a vector quantity, as it has both magnitude and direction.

5. Application: Moment is primarily used in the study of rotational motion, equilibrium, and dynamics. It helps determine the stability and behavior of objects in rotational systems. Momentum, on the other hand, is used to analyze the motion of objects in linear systems, such as collisions and projectile motion.

To summarize, moment and momentum are distinct concepts in physics. Moment relates to rotational forces and equilibrium, while momentum relates to the linear motion of objects. Understanding the difference between these two terms is essential for comprehending various aspects of rotational and linear mechanics.

Difference between Twisting Moment and Torque

Definition of Twisting Moment

In the realm of physics and engineering, the concept of a “twisting moment” refers to the rotational force applied to an object. It is also known as a “torque.” The twisting moment is the product of the force applied to an object and the distance from the axis of rotation. It causes an object to rotate around an axis, just like how a wrench applies a twisting force to a bolt. The twisting moment is denoted by the symbol “M.”

Definition of Torque

Torque, like the twisting moment, is a measure of the rotational force applied to an object. It is the product of the force applied perpendicular to the distance from the axis of rotation. Torque is a vector quantity, meaning it has both magnitude and direction. In physics, torque is denoted by the symbol “τ” (tau). Torque is commonly used to describe the rotational motion of objects, such as the spinning of a wheel or the movement of a lever.

Comparison of Twisting Moment and Torque

While the terms “twisting moment” and “torque” are often used interchangeably, there are some subtle differences between the two. Let’s explore these differences:

1. Definition: The twisting moment and torque have slightly different definitions. The twisting moment specifically refers to the rotational force applied to an object, while torque encompasses both the force and the distance from the axis of rotation.

2. Units: The units of measurement for the twisting moment and torque are different. The twisting moment is typically measured in newton-meters (Nm), while torque is measured in newton-meters (Nm) or pound-feet (lb-ft) depending on the system of measurement used.

3. Direction: The twisting moment is a scalar quantity, meaning it only has magnitude and no specific direction. On the other hand, torque is a vector quantity and has both magnitude and direction. The direction of torque depends on the direction of the force applied and the direction of the distance from the axis of rotation.

4. Application: The terms “twisting moment” and “torque” are often used in different contexts. Twisting moment is commonly used in structural engineering to analyze the stability and strength of structures, such as beams and columns. Torque, on the other hand, is frequently used in mechanical engineering to describe the rotational motion of machines and mechanisms.

To summarize, while the terms “twisting moment” and “torque” are closely related and often used interchangeably, they have slight differences in their definitions, units of measurement, direction, and application. Understanding these differences can help in accurately describing and analyzing rotational forces in various fields of science and engineering.

Difference between Moment, Torque, and Couple

Definition of Moment

In physics, the term “moment” refers to the turning effect produced by a force around a point or axis. It is also known as the “torque” or “rotational force.” The moment is a vector quantity, meaning it has both magnitude and direction. It is denoted by the symbol “M” and is measured in newton-meters (Nm) or pound-feet (lb-ft).

Definition of Torque

Torque, like moment, is a measure of the rotational force acting on an object. It is defined as the product of the force applied and the distance from the axis of rotation. Torque is a vector quantity, meaning it has both magnitude and direction. It is denoted by the symbol “τ” and is measured in newton-meters (Nm) or pound-feet (lb-ft).

Definition of Couple

A couple is a pair of equal and opposite forces that act on a body but do not have a net force or a net moment. The forces in a couple are parallel to each other but act in opposite directions. Couples are often used to create rotational motion or maintain rotational equilibrium. The moment produced by a couple is equal to the product of one of the forces and the perpendicular distance between the forces.

Comparison of Moment, Torque, and Couple

Aspect	Moment	Torque	Couple
Definition	The turning effect produced by a force	The rotational force acting on an object	A pair of equal and opposite forces
Symbol	M	τ	–
Vector	Yes	Yes	No
Measurement	Newton-meters (Nm) or pound-feet (lb-ft)	Newton-meters (Nm) or pound-feet (lb-ft)	–
Direction	Yes	Yes	–
Net Force	No	No	No
Net Moment	No	No	No
Purpose	Produces rotational motion or maintains balance	Produces rotational motion or maintains balance	Produces rotational motion or maintains balance

To summarize, the moment and torque are essentially the same, referring to the rotational force acting on an object. They are both vector quantities and measured in newton-meters or pound-feet. On the other hand, a couple is a pair of equal and opposite forces that do not have a net force or net moment. Couples are used to create rotational motion or maintain rotational equilibrium.
Difference of Moment and Torque

Definition of Moment

In physics, the term “moment” refers to the turning effect or rotational force produced by an object. It is a measure of the ability of a force to cause an object to rotate about a specific point or axis. The moment is also known as the “torque” or “rotational force” and is denoted by the symbol “M”.

The moment of a force is calculated by multiplying the magnitude of the force by the perpendicular distance between the point of rotation and the line of action of the force. Mathematically, it can be expressed as:

Moment = Force × Perpendicular Distance

The SI unit of moment is the Newton-meter (Nm). Moments play a crucial role in understanding rotational motion, equilibrium, and dynamics in physics.

Definition of Torque

Torque, on the other hand, is a term commonly used in engineering and mechanics to describe the rotational force acting on an object. It is a measure of the force’s ability to cause an object to rotate around an axis. Torque is denoted by the symbol “τ” and is calculated using the formula:

Torque = Force × Lever Arm

The lever arm is the perpendicular distance between the axis of rotation and the line of action of the force. The SI unit of torque is also the Newton-meter (Nm). Torque is an essential concept in understanding angular motion, equilibrium, and mechanics.

Comparison of Moment and Torque

While the terms “moment” and “torque” are often used interchangeably, there are subtle differences between them. Here are some key points of comparison:

1. Definition: Moment and torque both refer to rotational forces, but moment is a more general term that encompasses both rotational and turning effects. Torque, on the other hand, specifically refers to the rotational force acting on an object.

2. Usage: Moment is commonly used in physics, while torque is predominantly used in engineering and mechanics.

3. Calculation: The calculation of moment involves multiplying the force by the perpendicular distance, whereas torque is calculated by multiplying the force by the lever arm.

4. Direction: Moment is a vector quantity and has both magnitude and direction. It follows the right-hand rule, where the direction of the moment is perpendicular to the plane formed by the force and the lever arm. Torque, on the other hand, is also a vector quantity but is often represented by a signed scalar value, indicating the direction of rotation.

5. Application: Moment is used to analyze rotational motion, equilibrium, and dynamics in physics. It helps in understanding the behavior of objects under the influence of rotational forces. Torque, on the other hand, is primarily used in mechanical systems to analyze the effectiveness of forces in causing rotational motion.

In summary, while moment and torque are related concepts that describe rotational forces, they differ in their definitions, usage, calculation methods, directionality, and applications. Understanding these differences is crucial for comprehending the principles of rotational mechanics and their practical applications in various fields.

Difference between Angular Momentum and Torque

Definition of Angular Momentum

Angular momentum is a fundamental concept in physics that describes the rotational motion of an object. It is a vector quantity that depends on both the mass and the distribution of mass within the object, as well as its rotational speed. Angular momentum is denoted by the symbol “L” and is measured in units of kilogram meters squared per second (kg·m²/s).

In simpler terms, angular momentum is a measure of how much rotational motion an object possesses. It takes into account not only the object’s mass but also how that mass is distributed around its axis of rotation. For example, a spinning figure skater with her arms extended has a greater angular momentum than when she pulls her arms closer to her body, as her mass is distributed farther from her axis of rotation.

Definition of Torque

Torque, on the other hand, is a measure of the rotational force acting on an object. It is the product of the force applied to an object and the distance from the axis of rotation at which the force is applied. Torque is denoted by the symbol “τ” and is measured in units of newton meters (N·m).

To better understand torque, imagine trying to open a door. When you push or pull on the door handle, you are applying a force that creates a torque around the door‘s hinges. The farther away from the hinges you apply the force, the greater the torque will be. This is why it’s easier to open a door by pushing on the outer edge of the handle rather than close to the hinges.

Comparison of Angular Momentum and Torque

While both angular momentum and torque are related to rotational motion, they represent different aspects of it. Here are some key differences between the two:

1. Definition: Angular momentum is a measure of an object’s rotational motion, taking into account its mass and distribution of mass. Torque, on the other hand, is a measure of the rotational force acting on an object.

2. Units: Angular momentum is measured in kilogram meters squared per second (kg·m²/s), while torque is measured in newton meters (N·m).

3. Formula: The formula for angular momentum is L = Iω, where L is angular momentum, I is the moment of inertia, and ω is the angular velocity. The formula for torque is τ = rF, where τ is torque, r is the distance from the axis of rotation, and F is the force applied.

4. Effect on Rotation: Angular momentum affects the overall rotational motion of an object, while torque determines how an object’s rotation changes over time. Angular momentum is conserved in the absence of external torques, meaning it remains constant unless acted upon by an external force. Torque, on the other hand, can cause an object to start rotating, stop rotating, or change its rotational speed.

To summarize, angular momentum describes the rotational motion of an object, taking into account its mass and distribution of mass, while torque measures the rotational force acting on an object. While both concepts are related to rotational motion, they represent different aspects of it and have distinct formulas and units. Understanding the difference between angular momentum and torque is crucial in the study of rotational dynamics and mechanics.

Difference between Moment and Torsion

Definition of Moment

In physics, the term “moment” refers to the turning effect produced by a force around a point or an axis. It is also known as “torque” in the context of rotational motion. Moment is a vector quantity, which means it has both magnitude and direction. The magnitude of the moment is given by the product of the force applied and the perpendicular distance from the point of rotation to the line of action of the force.

Definition of Torsion

Torsion, on the other hand, is a specific type of moment that occurs when a torque is applied to a solid object, causing it to twist. It is the rotational equivalent of tension or compression in linear mechanics. Torsion is commonly observed in objects such as shafts, springs, and beams, where the applied torque causes a twisting deformation.

Comparison of Moment and Torsion

While both moment and torsion involve rotational forces, there are some key differences between the two:

1. Definition: Moment is a general term that refers to the turning effect produced by a force, whereas torsion specifically refers to the twisting deformation caused by an applied torque.

2. Magnitude: Moment is calculated by multiplying the force applied by the perpendicular distance from the point of rotation to the line of action of the force. Torsion, on the other hand, is determined by the product of the applied torque and the polar moment of inertia, which is a measure of an object’s resistance to torsional deformation.

3. Direction: Moment is a vector quantity, meaning it has both magnitude and direction. The direction of the moment is perpendicular to the plane formed by the force and the line of action. Torsion, on the other hand, is typically described in terms of clockwise or counterclockwise rotation.

4. Applications: Moment is commonly used in various fields, including engineering, mechanics, and physics, to analyze rotational equilibrium, dynamics, and mechanics. Torsion, on the other hand, is specifically relevant in the design and analysis of structures and components subjected to twisting forces, such as drive shafts, helicopter rotor blades, and torsion springs.

To summarize, moment and torsion are related concepts in the realm of rotational mechanics. Moment refers to the turning effect produced by a force, while torsion specifically refers to the twisting deformation caused by an applied torque. Understanding the distinction between these terms is crucial for analyzing and designing systems involving rotational forces.

Difference between Moment and Momentum in English

Definition of Moment

In English, the term “moment” refers to a concept used in physics, particularly in the study of rotational motion and equilibrium. It is often used interchangeably with the term “torque.” The moment of a force is a measure of its ability to cause an object to rotate about a specific point or axis. It depends on the magnitude of the force and the distance between the point of rotation and the line of action of the force.

Definition of Momentum

On the other hand, “momentum” is a concept used to describe the motion of an object. It is a property of a moving object that depends on its mass and velocity. Momentum is a vector quantity, meaning it has both magnitude and direction. The magnitude of momentum is equal to the product of an object’s mass and its velocity.

Comparison of Moment and Momentum

While both moment and momentum are terms used in physics, they have distinct meanings and applications. Let’s take a closer look at the differences between these two concepts:

Moment	Momentum
Moment is related to rotational motion and equilibrium.	Momentum is related to the linear motion of an object.
It is a measure of a force’s ability to cause rotation.	It is a measure of an object’s motion.
Moment depends on the magnitude of the force and the distance from the point of rotation.	Momentum depends on an object’s mass and velocity.
Moment is a scalar quantity.	Momentum is a vector quantity.
The SI unit of moment is the Newton-meter (Nm).	The SI unit of momentum is kilogram-meter per second (kg·m/s).

In summary, moment and momentum are distinct concepts in physics. Moment is associated with rotational motion and equilibrium, while momentum describes the linear motion of an object. Moment depends on force and distance, whereas momentum depends on mass and velocity. Understanding these differences is crucial in comprehending the various aspects of rotational and linear dynamics.

What is the Difference between Moment and Momentum?

Explanation of Moment

In physics, the terms “moment” and “momentum” are often used interchangeably, but they actually refer to different concepts. Let’s start by understanding what moment means.

Moment is a term used in rotational mechanics to describe the turning effect or rotational force acting on an object. It is also known as torque. When a force is applied to an object, it can cause the object to rotate around a fixed point or axis. The moment of a force is a measure of its ability to cause this rotation.

To better understand the concept of moment, let’s consider a simple example. Imagine you have a door that is hinged on one side. When you push or pull the door handle, you are applying a force to the door. This force creates a moment or torque that causes the door to rotate around its hinge.

The magnitude of the moment depends on two factors: the magnitude of the force applied and the distance between the point of application of the force and the axis of rotation. Mathematically, the moment (M) is calculated as the product of the force (F) and the perpendicular distance (r) between the point of application and the axis of rotation: M = F * r.

Explanation of Momentum

Now let’s shift our focus to momentum, which is a different concept from moment.

Momentum is a term used to describe the quantity of motion possessed by an object. It is a vector quantity, meaning it has both magnitude and direction. Momentum depends on the mass and velocity of an object.

The momentum of an object can be calculated by multiplying its mass (m) by its velocity (v): p = m * v. The SI unit for momentum is kilogram-meter per second (kg·m/s).

To illustrate the concept of momentum, let’s consider a moving car. If two cars of the same mass are traveling at different velocities, the car with the higher velocity will have a greater momentum. This is because momentum takes into account both the mass and the velocity of an object.

Comparison of Moment and Momentum

Although both moment and momentum are related to the motion of objects, they have distinct meanings and applications.

Moment is specifically associated with rotational motion and describes the turning effect or rotational force acting on an object. It is calculated by multiplying the force applied to an object by the perpendicular distance between the point of application and the axis of rotation.

Momentum, on the other hand, is a measure of the quantity of motion possessed by an object. It takes into account both the mass and velocity of an object and is calculated by multiplying the mass of the object by its velocity.

In summary, moment is related to rotational motion and describes the turning effect or rotational force, while momentum is related to linear motion and describes the quantity of motion possessed by an object. Both concepts are important in understanding the dynamics of objects in motion, but they have different applications and calculations.

What is the relationship between moment and torque, and how does it relate to dry friction and its types explained?

The relationship between moment and torque is an important concept in physics and mechanics. Torque is the measure of the force that can cause an object to rotate around an axis, while moment refers to the turning effect produced by a force around a given point. Both concepts are closely related as torque is the product of force and the distance from the axis, while moment is the torque multiplied by the perpendicular distance between the point and the axis. Understanding this relationship is essential when exploring the concept of dry friction and its types explained. Dry friction acts between surfaces in contact and opposes the relative motion or tendency of motion between them. It can be classified into static friction, sliding friction, rolling friction, and fluid friction. To gain a deeper understanding of dry friction and its different types, you can refer to the article “Dry friction and its types explained”.

Frequently Asked Questions

What is the difference between moment of inertia and momentum?

Moment of inertia is a measure of an object’s resistance to changes in its rotational motion, while momentum is a measure of an object’s motion due to its mass and velocity.

What is the difference between torque and bending moment?

Torque refers to the rotational force applied to an object, while bending moment refers to the internal force that causes a beam or structure to bend.

What is the difference between angular momentum and torque?

Angular momentum is a measure of an object’s rotational motion, while torque is the force that causes an object to rotate or change its rotational motion.

What is the difference between moment of inertia and torque?

Moment of inertia is a property of an object that determines its resistance to changes in rotational motion, while torque is the force that causes an object to rotate.

What is the difference between moment and bending moment?

Moment refers to the turning effect of a force about a point, while bending moment specifically refers to the internal force that causes a beam or structure to bend.

What is the difference between moment arm and torque?

Moment arm is the perpendicular distance between the line of action of a force and the axis of rotation, while torque is the product of the force and the moment arm.

What is the difference between moment couple and torque?

A moment couple refers to two equal and opposite forces that act on an object but do not produce any linear motion, while torque refers to a single force that causes an object to rotate.

What is the difference between moments and torque?

Moments refer to the turning effects of forces about a point, while torque specifically refers to the turning effect of a force about an axis of rotation.

Why is torque called moment?

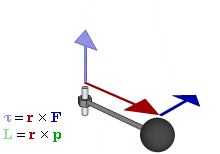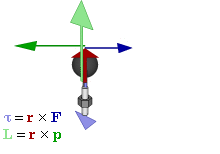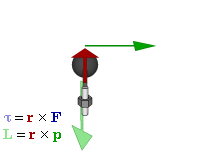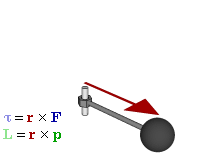
Torque is called moment because it is a measure of the turning effect or rotational force applied to an object.

What is the difference between moment and bending moment?

Moment refers to the turning effect of a force about a point, while bending moment specifically refers to the internal force that causes a beam or structure to bend.

What is the difference between moment and momentum?

Moment refers to the turning effect of a force about a point, while momentum is a measure of an object’s motion due to its mass and velocity.

Also Read:

• Difference between friction and viscosity
• How to find energy difference between orbitals
• Difference between damped oscillation and forced oscillation
• What s the difference between soft white and daylight bulbs at the store
• Potential energy vs potential difference
• Difference between velocity and acceleration
• How to calculate difference in energy levels
• Can potential difference be negative
• Velocity and speed difference
• How to calculate gravitational energy differences in gravitational time dilation experiments

Damped oscillation and forced oscillation are two different types of oscillatory motion. In damped oscillation, the amplitude of the oscillation gradually decreases over time due to the presence of damping forces, such as friction or air resistance. This results in the oscillation eventually coming to a stop. On the other hand, forced oscillation occurs when an external force is applied to a system, causing it to oscillate at a frequency determined by the force. The amplitude of the forced oscillation can vary depending on the frequency and magnitude of the applied force.

Key Takeaways

Damped Oscillation	Forced Oscillation
Amplitude decreases over time	Amplitude can vary
Damping forces present	External force applied
Oscillation comes to a stop	Oscillation continues
Frequency determined by system	Frequency determined by force

Understanding Oscillations

Oscillations are a fascinating phenomenon that can be observed in various systems, from mechanical systems to electrical circuits. They involve the repetitive back-and-forth motion of an object or a system around a central position. In simpler terms, oscillations refer to the regular swinging or vibrating motion of an object.

Definition of Oscillations

Oscillations can be defined as the periodic motion of an object or a system between two extreme points or positions. This motion is characterized by the presence of a restoring force that brings the object back to its equilibrium position. The restoring force acts in the opposite direction to the displacement of the object, causing it to oscillate around the equilibrium point.

In the context of oscillations, several key terms are important to understand:

1. Amplitude: The maximum displacement of an oscillating object from its equilibrium position.
2. Periodic Force: An external force that is applied periodically to an oscillating system, causing it to oscillate.
3. Restoring Force: The force that acts on an object or a system, bringing it back to its equilibrium position.
4. Oscillation Frequency: The number of complete oscillations or cycles that occur in a given time period.
5. Oscillation Period: The time taken for one complete oscillation or cycle to occur.
6. Phase Difference: The difference in phase between two oscillating objects or systems.
7. Damping Force: The force that opposes the motion of an oscillating object, leading to energy dissipation and a decrease in amplitude.
8. Damping Coefficient: A measure of the damping force in an oscillating system.
9. Damping Ratio: The ratio of the actual damping coefficient to the critical damping coefficient.
10. Critical Damping: The damping condition where the oscillating system returns to its equilibrium position without any oscillation.
11. Underdamping: The damping condition where the oscillating system experiences oscillations that gradually decrease in amplitude.
12. Overdamping: The damping condition where the oscillating system returns to its equilibrium position without oscillating, but with a slower rate of convergence.
13. Transient State: The initial phase of an oscillation where the system’s behavior is influenced by its initial conditions.
14. Steady State Oscillation: The long-term behavior of an oscillating system after the transient state has passed.
15. Natural Frequency: The frequency at which an oscillating system tends to oscillate in the absence of any external force.
16. Resonance: The phenomenon where an oscillating system is forced to oscillate at its natural frequency by an external force.
17. Resonance Frequency: The frequency at which resonance occurs in an oscillating system.
18. Harmonic Oscillator: A system that exhibits simple harmonic motion, where the restoring force is directly proportional to the displacement.

Types of Oscillations

Oscillations can be classified into different types based on various factors. Some common types of oscillations include:

1. Free Oscillation: Also known as natural or unforced oscillation, it occurs when an oscillating system is left to oscillate on its own without any external force.
2. Driven Oscillation: This type of oscillation occurs when an external force is continuously applied to an oscillating system, causing it to oscillate at a frequency different from its natural frequency.
3. Forced Vibration: When an oscillating system is subjected to an external force that matches its natural frequency, it undergoes forced vibration, resulting in large amplitude oscillations.
4. Mechanical Resonance: The phenomenon where an oscillating system vibrates with maximum amplitude at its natural frequency due to the resonance effect.
5. Oscillation System: A system that exhibits oscillatory motion, such as a pendulum, a mass-spring system, or an electrical LC circuit.

Understanding oscillations is crucial in various fields, including physics, engineering, and even music. By studying the behavior of oscillating systems, we can gain insights into the fundamental principles that govern the motion of objects and systems in our world.

Damped Oscillations

Definition and Explanation of Damped Oscillations

Damped oscillations refer to a type of oscillatory motion where the amplitude of the oscillations gradually decreases over time due to the presence of a damping force. In simple terms, it is the motion of a system that experiences energy dissipation, causing the oscillations to gradually come to a stop.

To understand damped oscillations better, let’s consider a harmonic oscillator, which is a mechanical system that exhibits oscillatory motion. In a harmonic oscillator, there are two main forces at play: the restoring force and the damping force. The restoring force acts to bring the system back to its equilibrium position, while the damping force opposes the motion and dissipates energy.

The behavior of damped oscillations is influenced by various factors, including the damping coefficient, the mass of the system, and the external forces acting on it. The damping coefficient determines the strength of the damping force, while the mass affects the natural frequency of the system. When the damping force is relatively weak compared to the restoring force, the system exhibits underdamping. On the other hand, if the damping force is too strong, the system shows overdamping. Critical damping occurs when the damping force is just enough to prevent oscillations from continuing indefinitely.

Factors affecting Damped Oscillations

Several factors can affect the behavior of damped oscillations:

1. Damping coefficient: The damping coefficient determines the strength of the damping force. A higher damping coefficient leads to faster energy dissipation and a quicker decay of the oscillations.

2. Mass of the system: The mass of the system affects the natural frequency of the oscillations. A higher mass results in a lower natural frequency, which in turn affects the rate at which the oscillations decay.

3. External forces: The presence of external forces can influence the behavior of damped oscillations. Periodic forces with frequencies close to the natural frequency of the system can cause resonance, leading to larger oscillations.

Real-world examples of Damped Oscillations

Damped oscillations can be observed in various real-world phenomena. Here are a few examples:

1. Pendulum: A swinging pendulum experiences damping due to air resistance. Over time, the pendulum‘s oscillations gradually decrease in amplitude until it comes to a stop.

2. Car suspension system: The suspension system of a car undergoes damped oscillations when encountering bumps or uneven road surfaces. The damping force helps absorb the energy and prevents excessive bouncing.

3. Musical instruments: Instruments like pianos, guitars, and drums exhibit damped oscillations when their strings or membranes are struck. The damping force helps control the decay of sound and prevents prolonged vibrations.

Forced Oscillations

Definition and Explanation of Forced Oscillations

Forced oscillations refer to the phenomenon where an oscillating system is subjected to an external periodic force, causing it to deviate from its natural frequency and amplitude. In simple terms, it is the forced vibration of a system that is driven by an external force.

When a mechanical oscillation system is subjected to a periodic force, it undergoes oscillatory motion known as forced oscillations. This external force can be of any frequency and amplitude, and it can either be in phase or out of phase with the system’s natural frequency. The system responds to this external force by oscillating with a frequency equal to the frequency of the applied force.

The behavior of forced oscillations is influenced by various factors, including the damping force, energy dissipation, and the natural frequency of the system. Let’s explore these factors in more detail.

Factors affecting Forced Oscillations

1. Damping Force: The damping force in a system plays a crucial role in forced oscillations. It determines the rate at which energy is dissipated from the system. The damping force can be classified into three categories: underdamping, overdamping, and critical damping. Underdamping occurs when the damping force is less than the critical damping, resulting in oscillations with a decreasing amplitude. Overdamping occurs when the damping force is greater than the critical damping, leading to slow decay of oscillations. Critical damping occurs when the damping force is equal to the critical damping, resulting in the fastest decay of oscillations.

2. Natural Frequency: The natural frequency of an oscillating system is the frequency at which it vibrates in the absence of any external force. When a periodic force is applied to the system, it can either be in resonance or out of resonance with the natural frequency. Resonance occurs when the frequency of the external force matches the natural frequency of the system, leading to a significant increase in the amplitude of oscillations. Out of resonance occurs when the frequency of the external force is different from the natural frequency, resulting in smaller amplitudes.

3. Amplitude and Phase Difference: The amplitude of forced oscillations depends on the amplitude of the external force. If the external force has a large amplitude, the oscillations will also have a large amplitude. The phase difference between the external force and the system’s response also affects the behavior of forced oscillations. In-phase forces result in maximum energy transfer, while out-of-phase forces result in energy cancellation.

Real-world examples of Forced Oscillations

Forced oscillations can be observed in various real-world scenarios. Here are a few examples:

1. Pendulum Clock: The swinging motion of a pendulum clock is an example of forced oscillations. The periodic force applied by the clock mechanism keeps the pendulum oscillating at a constant frequency.

2. Musical Instruments: When a musician plays a musical instrument, the strings or air columns in the instrument are forced to vibrate at specific frequencies, producing different notes. The musician controls the external force applied to the instrument to create the desired sound.

3. Suspension System in Vehicles: The suspension system in vehicles is designed to dampen the oscillations caused by uneven road surfaces. The system uses springs and dampers to absorb the external forces and minimize the impact on the vehicle’s body.

Difference between Damped Oscillation and Forced Oscillation

Damped oscillation and forced oscillation are two types of mechanical oscillations that exhibit different behaviors and characteristics.

Comparative Analysis of Damped and Forced Oscillations

Damped oscillation refers to the oscillatory motion of a system that experiences energy dissipation due to the presence of a damping force. This damping force causes the amplitude of the oscillation to decrease over time, eventually bringing the system to a rest. In contrast, forced oscillation occurs when an external force is applied to a system, causing it to oscillate at a frequency different from its natural frequency.

One key difference between damped and forced oscillations lies in their energy behavior. In damped oscillation, energy is gradually dissipated due to the damping force, resulting in a decrease in the amplitude of the oscillation. On the other hand, in forced oscillation, energy is continuously supplied to the system by the external force, allowing the oscillation to persist.

Another difference is observed in the response of the system to the applied force. In damped oscillation, the system’s response is influenced by both the damping force and the external force. The amplitude of the oscillation is determined by the balance between these two forces. In forced oscillation, the amplitude of the oscillation is primarily determined by the characteristics of the external force, such as its frequency and magnitude.

How Damping affects Forced Oscillations

The presence of damping in a forced oscillation system can significantly affect its behavior. The damping force can modify the amplitude, phase, and frequency response of the system. When the damping force is small, the system exhibits underdamping, where the amplitude of the oscillation is reduced but the frequency remains close to the natural frequency. In the case of overdamping, the system takes a longer time to return to its equilibrium position after being displaced.

The damping ratio, which represents the ratio of the actual damping to the critical damping, plays a crucial role in determining the response of the system. A higher damping ratio leads to a faster decay of the amplitude and a wider frequency response. Conversely, a lower damping ratio results in a slower decay of the amplitude and a narrower frequency response.

The role of external force in Damped and Forced Oscillations

In damped oscillation, the external force is not required for the system to oscillate. The system can undergo undriven oscillation, where it oscillates naturally at its own frequency. However, the presence of an external force can still affect the behavior of the system, altering its amplitude and phase.

In forced oscillation, the external force is essential for the system to oscillate. The system responds to the periodic force by oscillating at the frequency of the applied force. The amplitude of the forced oscillation depends on the frequency of the external force and the resonance frequency of the system. When the frequency of the external force matches the resonance frequency, the system exhibits resonance, resulting in a significant increase in the amplitude.

Special Case: Free Damped vs Forced Oscillations

Understanding Free Damped Oscillations

In the realm of mechanical oscillations, we encounter two fascinating phenomena: free damped oscillations and forced oscillations. Let’s delve into the intricacies of free damped oscillations first.

Free damped oscillations occur when a mechanical system, such as a harmonic oscillator, undergoes oscillatory motion in the absence of any external force. The motion is influenced by a damping force, which leads to energy dissipation over time. This damping force arises due to various factors like friction, air resistance, or other dissipative forces present in the system.

The behavior of free damped oscillations is characterized by the system’s natural frequency, damping ratio, and initial conditions. The natural frequency represents the frequency at which the system oscillates in the absence of damping. It is determined by the mass and stiffness of the system.

The amplitude of the oscillation gradually decreases over time due to the energy dissipation caused by the damping force. Eventually, the system reaches a state of equilibrium known as the steady state oscillation. In this state, the amplitude remains constant, and the system exhibits periodic motion.

The damping ratio plays a crucial role in free damped oscillations. It determines the type of damping present in the system: underdamping, overdamping, or critical damping. Underdamping occurs when the damping ratio is less than 1, resulting in oscillations with a gradually decreasing amplitude. Overdamping, on the other hand, occurs when the damping ratio is greater than 1, leading to slower and smoother oscillations. Critical damping occurs when the damping ratio is exactly 1, resulting in the fastest return to equilibrium without any oscillations.

Comparing Free Damped Oscillations with Forced Oscillations

Now that we have a good understanding of free damped oscillations, let’s compare them with forced oscillations.

Forced oscillations occur when a periodic force is applied to a mechanical system, causing it to oscillate at a frequency different from its natural frequency. This external force can be of various forms, such as vibrations, sound waves, or any other form of disturbance.

In forced oscillations, the system responds to the applied force by oscillating at the frequency of the external force. The amplitude of the oscillation depends on the resonance frequency, which is the frequency at which the system responds most strongly to the external force. When the resonance frequency matches the frequency of the external force, the system exhibits resonance, resulting in a significant increase in the amplitude of the oscillation.

One key difference between free damped oscillations and forced oscillations is the presence of the external force in the latter. While free damped oscillations occur naturally in the absence of any external force, forced oscillations require an external force to induce the oscillatory motion.

Damped oscillation occurs when an oscillating system gradually loses energy due to the presence of a damping force. This results in the amplitude of the oscillation decreasing over time until it eventually comes to rest. Damped oscillation is commonly observed in systems such as a swinging pendulum or a vibrating spring with friction.

On the other hand, forced oscillation occurs when an external force is applied to an oscillating system. This external force drives the system to oscillate at a specific frequency, known as the driving frequency. The amplitude of the forced oscillation depends on the frequency and magnitude of the applied force.

While both damped and forced oscillations involve the motion of an object back and forth, they differ in terms of the energy loss and the presence of an external driving force. Understanding these differences is crucial in various fields, including physics, engineering, and even music.

What is the difference between damped oscillation and forced oscillation, and how does it relate to the concept of overdamped and critically damped?

Damped oscillation refers to the phenomenon where the amplitude of an oscillating system gradually decreases over time due to energy dissipation. On the other hand, forced oscillation occurs when an external force causes a system to oscillate at a specific frequency. The concepts of overdamped and critically damped are related to damped oscillation and describe different behavior patterns. Difference between overdamped and critically damped. In overdamped systems, the damping force is greater than necessary to bring the system to equilibrium, resulting in slower decay and no oscillation. Critically damped systems reach equilibrium in the shortest possible time without any oscillation. Both these concepts illustrate different ways in which damping affects the behavior of oscillating systems.

Frequently Asked Questions

What is the difference between damped oscillation and forced oscillation?

Damped oscillation refers to the oscillatory motion where the amplitude of oscillation decreases over time due to the presence of a damping force, which leads to energy dissipation. On the other hand, forced oscillation is when an external force drives the oscillation at a frequency that may be different from the system’s natural frequency.

How do the differences between damped and forced oscillation affect the amplitude of the oscillation?

In damped oscillation, the amplitude decreases over time due to energy dissipation caused by the damping force. However, in forced oscillation, the amplitude is determined by the balance between the driving force and the damping force. If the driving force’s frequency matches the system’s natural frequency, the amplitude can increase significantly, a phenomenon known as resonance.

What is the difference between free damped and forced oscillations?

Free damped oscillation is a type of oscillatory motion where there is no external force acting on the system, and the amplitude decreases over time due to the damping force. On the contrary, forced oscillation occurs when an external force drives the system, and the amplitude does not necessarily decrease over time.

How does the damping ratio affect the type of damping in a mechanical oscillation?

The damping ratio determines the type of damping in a mechanical oscillation. If the damping ratio is less than 1, it’s underdamping, and the system oscillates with a gradually decreasing amplitude. If the damping ratio equals 1, it’s critical damping, and the system returns to equilibrium as quickly as possible without oscillating. If the damping ratio is greater than 1, it’s overdamping, and the system returns to equilibrium without oscillating but slower than in critical damping.

What is the difference between undriven and driven oscillation?

Undriven oscillation, also known as free oscillation, occurs when no external force is applied to the system after it is displaced from its equilibrium position. The frequency of this oscillation is the natural frequency of the system. Driven oscillation, also known as forced oscillation, occurs when an external force drives the system at a frequency that can be different from its natural frequency.

How does the oscillation period relate to the natural frequency and amplitude in simple harmonic motion?

In simple harmonic motion, the oscillation period is the time it takes for one complete cycle of oscillation. It is inversely proportional to the natural frequency of the system and is independent of the amplitude.

How does the restoring force contribute to the oscillatory motion?

The restoring force is the force that brings a system back to its equilibrium position. In oscillatory motion, it is proportional to the displacement from the equilibrium position and acts in the opposite direction. This force is responsible for the system’s tendency to oscillate around its equilibrium position.

What is the role of the damping coefficient in the oscillation equation?

The damping coefficient is a parameter in the oscillation equation that represents the amount of damping in the system. It determines how quickly the oscillations die out. A larger damping coefficient means more rapid energy dissipation and quicker damping of oscillations.

How does resonance occur in a forced vibration system?

Resonance in a forced vibration system occurs when the frequency of the external force matches the natural frequency of the system. This causes the amplitude of the oscillation to increase significantly, leading to large oscillations.

What is the significance of phase difference in steady state oscillation?

The phase difference in steady state oscillation refers to the difference in phase between the driving force and the response of the system. It provides information about how much the response of the system lags or leads the driving force. This phase difference depends on the damping and the difference between the driving frequency and the system’s natural frequency.

Also Read:

• Difference between friction and viscosity
• Difference between internal and external forces
• Potential energy vs potential difference
• How to calculate gravitational energy differences in gravitational time dilation experiments
• How to find energy difference between orbitals
• What s the difference between uv a and uv b light and how do they impact our skin
• Can potential difference be negative
• How to calculate energy difference
• How to find the energy difference between orbitals
• Velocity and speed difference