Calculate - lambdageeks.com

How To Calculate Drag Coefficient: Several Entities And Facts

January 20, 2024February 15, 2022 by Keerthi Murthi

How to Calculate Drag Coefficient

The drag coefficient is an essential parameter used to quantify the resistance an object experiences as it moves through a fluid medium, such as air or water. It plays a crucial role in understanding and predicting the aerodynamic behavior of various objects and scenarios. In this blog post, we will explore the definition, importance, factors influencing the drag coefficient, and different methods of calculating it. So, let’s dive in!

Definition and Importance of Drag Coefficient

how to calculate drag coefficient — Image by SchnellGewehr – Wikimedia Commons, Wikimedia Commons, Licensed under CC BY-SA 4.0.

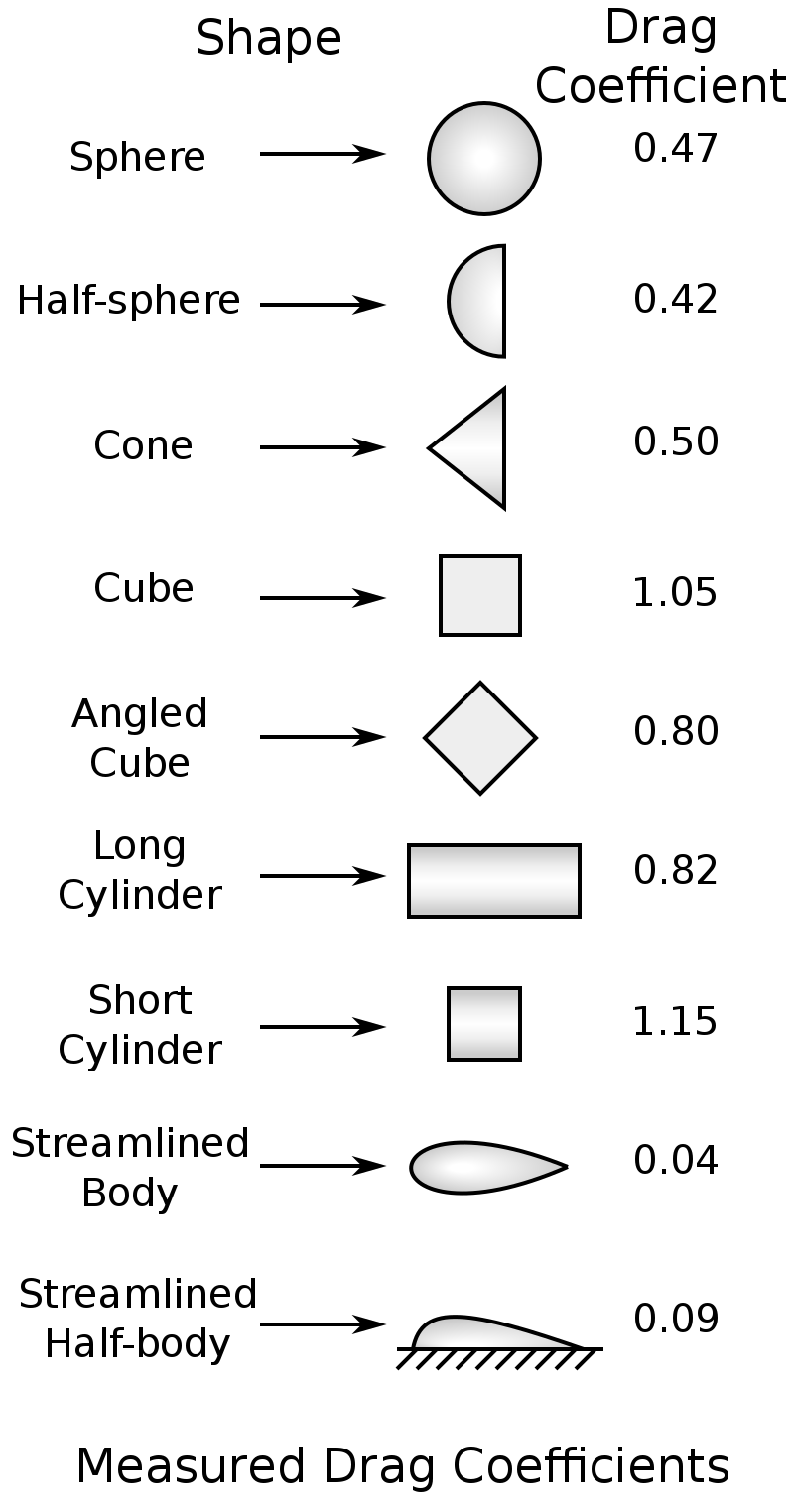
The drag coefficient is a dimensionless quantity that relates the drag force experienced by an object moving through a fluid to the reference area, flow velocity, and fluid density. It is denoted by the symbol Cd and is widely used in the fields of fluid dynamics, aerospace engineering, and automotive design.

The drag force is the resistance force exerted by the fluid on the object in the direction opposite to its motion. It depends on the shape, size, and surface characteristics of the object. By quantifying the drag force through the drag coefficient, engineers and researchers can assess the aerodynamic performance of vehicles, structures, or any object moving through a fluid medium.

The drag coefficient is crucial in determining other aerodynamic properties like the lift-to-drag ratio, which measures the efficiency of an object in generating lift compared to the drag it experiences. A low drag coefficient is desirable as it indicates lower air resistance and improved fuel efficiency, speed, and maneuverability.

Factors Influencing Drag Coefficient

Several factors influence the drag coefficient of an object. Let’s take a look at some of the key factors:

Shape and Surface Characteristics: The shape of an object significantly affects its drag coefficient. Streamlined or aerodynamic shapes, like teardrops, minimize drag by reducing the separation of the fluid flow. Surface roughness, coatings, and protrusions also impact the drag coefficient.
Reynolds Number: The Reynolds number is a dimensionless parameter that characterizes the flow regime around an object. It depends on the flow velocity, object size, and fluid properties. The drag coefficient can vary with the Reynolds number, transitioning between laminar and turbulent flows.
Flow Velocity: Higher flow velocities generally result in higher drag coefficients. As the fluid flow speed increases, the momentum transfer and pressure distribution around the object change, leading to increased drag.
Boundary Layer: The boundary layer is the thin layer of fluid adjacent to the object’s surface. The behavior of the boundary layer, whether laminar or turbulent, affects the drag coefficient. Turbulent boundary layers tend to have higher drag coefficients.

Now that we understand the basics of drag coefficient let’s explore how to calculate it using different software and simulations.

Calculating Drag Coefficient in Different Software and Simulations

How to Calculate Drag Coefficient in Paraview

Paraview is a popular open-source data visualization and analysis software used in various scientific and engineering fields. To calculate the drag coefficient in Paraview, you would typically follow these steps:

Import the simulation results or data representing the fluid flow around the object into Paraview.
Identify a suitable surface on the object for calculating the drag coefficient.
Compute the drag force acting on the surface using the pressure and velocity data from the simulation.
Calculate the reference area, which is the projected area of the surface perpendicular to the flow direction.
Finally, divide the drag force by the product of the fluid density, flow velocity squared, and reference area to obtain the drag coefficient.

How to Calculate Drag Coefficient in CFD

Computational Fluid Dynamics (CFD) is a powerful tool for simulating and analyzing fluid flow and aerodynamic behavior. To calculate the drag coefficient using CFD, you generally follow these steps:

Set up the geometry and boundary conditions of the object and the fluid domain in the CFD software.
Define the flow properties, such as fluid density and viscosity, and the flow velocity.
Run the CFD simulation to solve the governing equations for fluid flow and obtain the pressure and velocity fields.
Identify the surface(s) of interest and extract the relevant data, such as pressure and velocity, from the simulation results.
Calculate the drag force acting on the surface(s) by integrating the pressure distribution along the surface.
Determine the reference area and divide the drag force by the appropriate terms to obtain the drag coefficient.

How to Calculate Drag Coefficient in Solidworks

Solidworks is a widely used 3D computer-aided design (CAD) software that also offers tools for simulating fluid flow and analyzing aerodynamic performance. To calculate the drag coefficient in Solidworks, you would typically follow these steps:

Create or import the 3D model of the object into Solidworks.
Define the fluid properties, such as density and viscosity, and the flow conditions, including velocity and temperature.
Set up the appropriate boundary conditions and mesh the fluid domain.
Run the fluid flow simulation and obtain the pressure and velocity data.
Identify the surface(s) on the object for which you want to calculate the drag coefficient.
Calculate the drag force acting on the surface(s) by integrating the pressure distribution.
Determine the reference area and divide the drag force by the product of fluid density, flow velocity squared, and reference area to obtain the drag coefficient.

How to Calculate Drag Coefficient in Ansys Fluent

Ansys Fluent is a powerful computational fluid dynamics (CFD) software widely used in various industries for simulating and analyzing fluid flow and aerodynamics. To calculate the drag coefficient using Ansys Fluent, you would typically follow these steps:

Set up the geometry and boundary conditions of the object and the fluid domain in Ansys Fluent.
Define the fluid properties, such as density and viscosity, and the flow conditions, including velocity and turbulence model.
Mesh the fluid domain appropriately to capture the flow features and capture the surface details of the object.
Run the CFD simulation and obtain the pressure and velocity fields.
Identify the surface(s) on the object for which you want to calculate the drag coefficient.
Calculate the drag force acting on the surface(s) by integrating the pressure distribution along the surface.
Determine the reference area and divide the drag force by the product of fluid density, flow velocity squared, and reference area to obtain the drag coefficient.

Calculating Drag Coefficient for Different Objects and Scenarios

Now that we have explored different software and simulations, let’s understand how to calculate the drag coefficient for various objects and scenarios.

How to Calculate Drag Coefficient of a Bullet

To calculate the drag coefficient of a bullet, you would typically perform wind tunnel tests or use computational simulations. In wind tunnel tests, the bullet is subjected to controlled airflow, and the drag force is measured. The drag coefficient is then calculated using the same formula we discussed earlier.

How to Calculate Drag Coefficient of an Airfoil

The drag coefficient of an airfoil depends on its shape, angle of attack, and Reynolds number. Wind tunnel tests or computational simulations are commonly used to determine the drag coefficient for different airfoil designs and operating conditions.

How to Calculate Drag Coefficient of a Car

The drag coefficient of a car is of significant importance in automotive design and fuel efficiency. It is typically determined through wind tunnel tests or computational simulations using software like Solidworks or Ansys Fluent.

How to Calculate Drag Coefficient of a Rocket

The drag coefficient of a rocket depends on its shape, size, and flight conditions. Computational simulations using software like CFD are commonly used to calculate the drag coefficient for rockets.

How to Calculate Drag Coefficient of a Parachute

The drag coefficient of a parachute is crucial in understanding its performance during descent. Wind tunnel tests or computational simulations are used to calculate the drag coefficient for different parachute designs.

How to Calculate Drag Coefficient of a Sphere

The drag coefficient of a sphere depends on its size and Reynolds number. It can be calculated through wind tunnel tests or using empirical correlations available for different flow regimes.

How to Calculate Drag Coefficient of a Cylinder

The drag coefficient of a cylinder is influenced by its aspect ratio, surface roughness, and Reynolds number. It can be determined through wind tunnel tests or computational simulations.

Additional Considerations in Drag Coefficient Calculation

Let’s address a few additional considerations when calculating the drag coefficient:

Does Drag Coefficient Change with Size?

Yes, the drag coefficient can vary with the size of the object. It is influenced by the object’s shape and surface characteristics, which can change as the size scales. Therefore, it is essential to consider size effects when analyzing and comparing drag coefficients.

Does Drag Coefficient Have Units?

The drag coefficient is a dimensionless quantity and does not have any units. It is derived from the ratio of the drag force to the product of fluid density, flow velocity squared, and reference area.

How to Calculate Drag Coefficient from Pressure Coefficient

The pressure coefficient is a dimensionless quantity that measures the deviation of the local pressure from the ambient pressure. It is often used to calculate the drag coefficient. The drag coefficient can be obtained by integrating the pressure coefficient along the surface and applying appropriate formulas.

And that concludes our exploration of how to calculate the drag coefficient! We have covered its definition, importance, factors influencing it, different software and simulations, and calculations for various objects and scenarios. Understanding and accurately determining the drag coefficient is crucial for optimizing the performance and efficiency of vehicles, structures, and other objects moving through a fluid medium. Happy calculating!

Numerical Problems on how to calculate drag coefficient

Problem 1:

A car is moving with a velocity of 25 m/s. The mass of the car is 1200 kg. The frontal area of the car is 2.5 m^2. Calculate the drag force acting on the car. Assume the drag coefficient (Cd) to be 0.35.

Solution:

Given:
Velocity of the car (V) = 25 m/s
Mass of the car (m) = 1200 kg
Frontal area of the car (A) = 2.5 m^2
Drag coefficient (Cd) = 0.35

The drag force (F) can be calculated using the formula:

$F = \frac{1}{2} \cdot Cd \cdot \rho \cdot A \cdot V^2$

where:
F = Drag force
Cd = Drag coefficient
ρ = Density of the fluid (air)
A = Frontal area of the object
V = Velocity of the object

Substituting the given values into the formula:

$F = \frac{1}{2} \cdot 0.35 \cdot \rho \cdot 2.5 \cdot (25)^2$

Problem 2:

A ball is thrown horizontally with an initial velocity of 20 m/s. The mass of the ball is 0.5 kg. The drag force acting on the ball is 10 N. Calculate the drag coefficient (Cd). Assume the density of air (ρ) to be 1.2 kg/m^3.

Solution:

Given:
Initial velocity of the ball (V) = 20 m/s
Mass of the ball (m) = 0.5 kg
Drag force (F) = 10 N
Density of air (ρ) = 1.2 kg/m^3

The drag force (F) can be calculated using the formula:

$F = \frac{1}{2} \cdot Cd \cdot \rho \cdot A \cdot V^2$

Rearranging the formula, we can solve for the drag coefficient (Cd):

$Cd = \frac{2F}{\rho \cdot A \cdot V^2}$

Substituting the given values into the formula:

$Cd = \frac{2 \cdot 10}{1.2 \cdot A \cdot (20)^2}$

Problem 3:

A swimmer is swimming in a pool with a velocity of 2 m/s. The mass of the swimmer is 70 kg. The drag force acting on the swimmer is 50 N. Calculate the drag coefficient (Cd). Assume the density of water (ρ) to be 1000 kg/m^3 and the frontal area of the swimmer (A) to be 0.8 m^2.

Solution:

Given:
Velocity of the swimmer (V) = 2 m/s
Mass of the swimmer (m) = 70 kg
Drag force (F) = 50 N
Density of water (ρ) = 1000 kg/m^3
Frontal area of the swimmer (A) = 0.8 m^2

The drag force (F) can be calculated using the formula:

$F = \frac{1}{2} \cdot Cd \cdot \rho \cdot A \cdot V^2$

Rearranging the formula, we can solve for the drag coefficient (Cd):

$Cd = \frac{2F}{\rho \cdot A \cdot V^2}$

Substituting the given values into the formula:

$Cd = \frac{2 \cdot 50}{1000 \cdot 0.8 \cdot (2)^2}$

Also Read:

How to Calculate Momentum Before Collision: Elastic, Inelastic, Formula and Problems

January 20, 2024January 6, 2022 by Manish Naik

Master calculating momentum before a collision: Explore formulas, tackle problems, and understand elastic and inelastic collisions.

Before we dive into the calculations, let’s first understand what momentum is. Momentum is a fundamental concept in physics that describes the motion of an object. It is defined as the product of an object’s mass and velocity. In simpler terms, momentum tells us how much “oomph” an object has when it is in motion.

Now, let’s explore how to calculate momentum before a collision. In this blog post, we will discuss the momentum formula, provide a step-by-step guide on how to calculate momentum, and explore factors that affect momentum before a collision. We will also compare momentum before and after a collision and discuss the principle of conservation of momentum.

How to Calculate Momentum Before Collision

Explanation of the Momentum Formula

The momentum of an object can be calculated using the following formula:

$text{Momentum (p)} = text{Mass (m)} times text{Velocity (v)}$

The formula states that momentum is equal to the product of an object’s mass and velocity. Mass refers to the amount of matter an object contains, while velocity is the speed at which the object is moving in a specific direction.

Step-by-Step Guide on How to Calculate Momentum

To calculate momentum before a collision, follow these steps:

Identify the mass of the object (m) in kilograms.
Determine the velocity of the object (v) in meters per second.
Multiply the mass and velocity to find the momentum (p) of the object.

Let’s take a look at an example to better understand this process.

Worked Out Example: Calculating Momentum Before Collision

Let’s say we have a car with a mass of 1000 kg traveling at a velocity of 20 m/s. To calculate the momentum before a collision, we can use the formula:

$text{Momentum (p)} = text{Mass (m)} times text{Velocity (v)}$

Substituting the given values into the formula, we have:

$text{Momentum (p)} = 1000 , text{kg} times 20 , text{m/s}$

Simplifying the calculation, we find:

$text{Momentum (p)} = 20000 , text{kg} cdot text{m/s}$

So, the momentum before the collision is 20000 kg·m/s.

Factors Affecting Momentum Before Collision

how to calculate momentum before collision — Image by Fizped – Wikimedia Commons, Wikimedia Commons, Licensed under CC BY 3.0.

Now that we know how to calculate momentum before a collision, let’s explore the factors that can affect it.

Mass of the Object

The mass of an object plays a crucial role in determining its momentum. The greater the mass, the greater the momentum. This means that an object with a larger mass will be harder to stop or change its motion.

Velocity of the Object

The velocity of an object also has a significant impact on its momentum. The higher the velocity, the greater the momentum. An object moving at a faster speed will have a larger momentum compared to an object moving at a slower speed.

Direction of the Object’s Movement

The direction in which an object is moving is vital in determining its momentum. Momentum is a vector quantity, meaning it has both magnitude and direction. Two objects with the same mass and velocity but moving in opposite directions will have equal magnitudes of momentum but different directions.

Comparing Momentum Before and After Collision

Now that we understand how to calculate momentum before a collision, let’s explore how we can compare momentum before and after a collision. In this scenario, we will consider the principle of conservation of momentum.

How to Calculate Momentum After Collision

When two objects collide, their momentum can be calculated using the same formula we discussed earlier:

$text{Momentum (p)} = text{Mass (m)} times text{Velocity (v)}$

However, to calculate the momentum after a collision, we need to consider the masses and velocities of both objects involved in the collision.

Understanding the Principle of Conservation of Momentum

The principle of conservation of momentum states that the total momentum of a system of objects remains constant before and after a collision, provided no external forces act on the system. In simpler terms, the total momentum before the collision will be equal to the total momentum after the collision.

Worked Out Example: Comparing Momentum Before and After Collision

Let’s consider a collision between two objects: a ball with a mass of 0.5 kg and a velocity of 10 m/s, and another ball with a mass of 0.3 kg and a velocity of -5 m/s. The negative velocity indicates the opposite direction of motion. To compare the momentum before and after the collision, we can follow these steps:

Calculate the momentum before the collision using the individual masses and velocities of the objects.
Determine the momentum after the collision using the masses and velocities of both objects after the collision.

By applying the formula for momentum, we can calculate the momentum before the collision as follows:

$text{Momentum (p)} = text{Mass (m)} times text{Velocity (v)}$

For the first ball, the momentum before the collision is:

$text{Momentum (p1)} = 0.5 , text{kg} times 10 , text{m/s} = 5 , text{kg} cdot text{m/s}$

For the second ball, the momentum before the collision is:

$text{Momentum (p2)} = 0.3 , text{kg} times (-5) , text{m/s} = -1.5 , text{kg} cdot text{m/s}$

Now, let’s consider the momentum after the collision. The total momentum of the system after the collision will be the sum of the individual momenta of the balls. Let’s assume the first ball stops after the collision, and the second ball continues moving in the same direction. Therefore, the momentum after the collision can be calculated as:

$text{Total Momentum (p)} = text{Momentum (p1)} + text{Momentum (p2)}$

Substituting the values we calculated earlier, we have:

$text{Total Momentum (p)} = 5 , text{kg} cdot text{m/s} + (-1.5 , text{kg} cdot text{m/s}) = 3.5 , text{kg} cdot text{m/s}$

So, the total momentum after the collision is 3.5 kg·m/s.

How is momentum calculated before a collision and in a system, and how do they relate to each other?

Calculating momentum in a system is an essential concept in physics, and it involves determining the mass and velocity of each object within the system. By using the formula p = mv, where p represents momentum, m is the mass, and v is the velocity, we can calculate the momentum of individual objects before a collision and the total momentum of the system. The link Calculating momentum in a system provides detailed information on how to perform these calculations. Understanding the momentum before a collision and in a system allows us to analyze and predict the resulting motion and energy changes during interactions between objects.

Numerical Problems on how to calculate momentum before collision

Problem 1:Two cars, A and B, are traveling towards each other on a straight road. Car A has a mass of 800 kg and is traveling at a velocity of 20 m/s towards the east. Car B has a mass of 1200 kg and is traveling at a velocity of 10 m/s towards the west. Calculate the momentum of each car before the collision.

Solution:
Given:
Mass of car A, $m_A = 800$ kg
Velocity of car A, $v_A = 20$ m/s (towards the east)
Mass of car B, $m_B = 1200$ kg
Velocity of car B, $v_B = -10$ m/s (towards the west)

The momentum of an object is given by the product of its mass and velocity.

The momentum of car A before collision, $p_A = m_A cdot v_A = 800 cdot 20 = 16000$ kg·m/s (towards the east)

The momentum of car B before collision, $p_B = m_B cdot v_B = 1200 cdot (-10) = -12000$ kg·m/s (towards the west)

Therefore, the momentum of car A before the collision is 16000 kg·m/s towards the east, and the momentum of car B before the collision is 12000 kg·m/s towards the west.

Problem 2: Two objects, X and Y, are moving towards each other on a frictionless surface. Object X has a mass of 2 kg and is moving towards the east with a velocity of 4 m/s. Object Y has a mass of 3 kg and is moving towards the west with a velocity of 6 m/s. Calculate the total momentum before the collision.

Solution:
Given:
Mass of object X, $m_X = 2$ kg
Velocity of object X, $v_X = 4$ m/s (towards the east)
Mass of object Y, $m_Y = 3$ kg
Velocity of object Y, $v_Y = -6$ m/s (towards the west)

The total momentum before the collision is the sum of the individual momenta of the objects.

The momentum of object X before collision, $p_X = m_X cdot v_X = 2 cdot 4 = 8$ kg·m/s (towards the east)

The momentum of object Y before collision, $p_Y = m_Y cdot v_Y = 3 cdot (-6) = -18$ kg·m/s (towards the west)

Total momentum before collision, $p_{text{total}} = p_X + p_Y = 8 + (-18) = -10$ kg·m/s

Therefore, the total momentum before the collision is -10 kg·m/s.

Problem 3: A stationary object X with a mass of 5 kg is struck by an object Y with a mass of 2 kg. Object Y is initially moving towards the east with a velocity of 10 m/s. After the collision, object X and object Y move together with a velocity of 4 m/s towards the west. Calculate the initial velocity of object X before the collision.

Solution:
Given:
Mass of object X, $m_X = 5$ kg
Mass of object Y, $m_Y = 2$ kg
Initial velocity of object Y, $v_{Y,text{initial}} = 10$ m/s (towards the east)
Final velocity of both objects, $v_{text{final}} = -4$ m/s (towards the west)

Let the initial velocity of object X be $v_{X,text{initial}}$ .

According to the law of conservation of momentum, the total momentum before the collision is equal to the total momentum after the collision.

The momentum of object X before collision, $p_{X,text{initial}} = m_X cdot v_{X,text{initial}}$

The momentum of object Y before collision, $p_{Y,text{initial}} = m_Y cdot v_{Y,text{initial}}$

The momentum after the collision, $p_{text{final}} = text{total mass} cdot v_{text{final}}$

Since the total mass after the collision is the sum of the masses of object X and object Y, $m_{text{total}} = m_X + m_Y$

Using the law of conservation of momentum:

$p_{X,text{initial}} + p_{Y,text{initial}} = p_{text{final}}$

$m_X cdot v_{X,text{initial}} + m_Y cdot v_{Y,text{initial}} = (m_X + m_Y) cdot v_{text{final}}$

Substituting the given values:

$5 cdot v_{X,text{initial}} + 2 cdot 10 = 5 + 2) cdot (-4)$

$5 cdot v_{X,text{initial}} + 20 = 7 cdot (-4)$

$5 cdot v_{X,text{initial}} = -28 - 20$

$5 cdot v_{X,text{initial}} = -48$

$v_{X,text{initial}} = frac{-48}{5} = -9.6$ m/s

Therefore, the initial velocity of object X before the collision is -9.6 m/s towards the west.

Also Read:

How to Find Net Force: Various Methods, Problems and Facts

January 20, 2024December 20, 2021 by Manish Naik

Net force is a fundamental concept in physics that helps us understand the motion of objects. It refers to the overall force acting on an object, taking into account both magnitude and direction. In this blog post, we will explore how to calculate net force, determine its direction, examine special cases, delve into practical applications, and highlight common mistakes and misconceptions.

How to Calculate Net Force

The Basic Net Force Equation

To calculate net force, we need to consider all the individual forces acting on an object. The basic equation for net force is:

$F_{text{net}} = F_1 + F_2 + F_3 + ldots$

Here, $F_{text{net}}$ represents the net force, and $F_1$ , $F_2$ , $F_3$ , and so on, represent the individual forces. Each force is a vector quantity, meaning it has both magnitude and direction.

Finding Net Force without Mass or Acceleration

In some cases, we may not have information about the mass or acceleration of an object. However, we can still determine the net force using Newton’s second law of motion, which states that the net force acting on an object is equal to the mass of the object multiplied by its acceleration:

$F_{text{net}} = m cdot a$

Here, $m$ represents the mass of the object, and $a$ represents its acceleration. By knowing the values of mass and acceleration, we can calculate the net force.

Calculating Net Force with Mass and Acceleration

In situations where we have both the mass and acceleration of an object, we can directly calculate the net force using the formula:

$F_{text{net}} = m cdot a$

For example, let’s consider a car with a mass of 1000 kilograms and an acceleration of 5 meters per second squared. By substituting these values into the formula, we find that the net force acting on the car is 5000 Newtons.

Determining the Direction of Net Force

how to find net force — Image by Raul654 – Wikimedia Commons, Wikimedia Commons, Licensed under CC BY-SA 3.0.

Understanding Vector Components

Since force is a vector quantity, it has both magnitude and direction. To determine the direction of net force, we need to break down the forces into their vector components. This involves resolving the forces into their horizontal (x) and vertical (y) components.

Finding Net Force in X and Y Directions

To find the net force in the x and y directions, we can use the following equations:

$F_{text{net}, x} = F_{1x} + F_{2x} + F_{3x} + ldots$

$F_{text{net}, y} = F_{1y} + F_{2y} + F_{3y} + ldots$

Here, $F_{text{net}, x}$ and $F_{text{net}, y}$ represent the net forces in the x and y directions, respectively. $F_{1x}$ , $F_{2x}$ , $F_{3x}$ , and so on, represent the x-components of the individual forces. Similarly, $F_{1y}$ , $F_{2y}$ , $F_{3y}$ , and so on, represent the y-components of the individual forces.

Calculating Net Force of Two Vectors

When dealing with two vectors at an angle, we can use trigonometry to find the net force. By breaking down the vectors into their x and y components and adding up the components separately, we can determine the net force.

For example, let’s consider two forces: $F_1$ with a magnitude of 10 Newtons at an angle of 30 degrees above the x-axis, and $F_2$ with a magnitude of 5 Newtons at an angle of 60 degrees below the x-axis. By finding the x and y components of each force and summing them up, we can calculate the net force.

Special Cases in Finding Net Force

Finding Net Force with Friction

When an object is moving on a surface, there are usually forces acting on it. The net force on the object is the vector sum of all the forces, including friction, that are acting on the object. Friction is a force that opposes the relative motion or tendency of such motion of two surfaces in contact. The magnitude of the frictional force $F_f$ can be calculated using the formula:

$F_f = mu cdot N$

where:

$F_f$ is the frictional force,
$μ$ is the coefficient of friction, which is a dimensionless scalar value that represents the frictional properties of the surfaces in contact,
$N$ is the normal force, which is the component of a contact force that is perpendicular to the surface that an object contacts.

The net force $F_{net}$ is the sum of all the forces acting on an object. When considering friction, this can be written as:

$F_{net} = F_{applied} - F_f$

where $F_{applied}$ is the external force applied to the object.

Now, let’s go through a worked-out example.

Example:

Suppose a 5 kg block is sliding on a horizontal surface. An external force of 30 N is applied to the block in the direction of motion. The coefficient of friction between the block and the surface is 0.4. What is the net force acting on the block?

Step 1: Calculate the normal force (N).

Since the block is on a horizontal surface and there’s no vertical acceleration, the normal force is equal to the weight of the block.

$N = m cdot g$

$N = 5 , text{kg} cdot 9.8 , text{m/s}^2$

$N = 49 , text{N}$

Step 2: Calculate the frictional force (F_f).

$F_f = mu cdot N$

$F_f = 0.4 cdot 49 , text{N}$

$F_f = 19.6 , text{N}$

Step 3: Calculate the net force (F_{net}).

$F_{net} = F_{applied} - F_f$

$F_{net} = 30 , text{N} - 19.6 , text{N}$

$F_{net} = 10.4 , text{N}$

So the net force acting on the block is 10.4 N in the direction of the applied force.

This net force will cause an acceleration according to Newton’s second law, $F = m \cdot a$ . To find this acceleration $a$ , we can rearrange the formula:

$a = frac{F_{net}}{m}$

$a = frac{10.4 , text{N}}{5 , text{kg}}$

$a = 2.08 , text{m/s}^2$

Calculating Net Force on an Inclined Plane

When dealing with objects on an inclined plane, the gravitational force acting on the object can be resolved into two components – one perpendicular to the plane and one parallel to it. The net force on the object is the sum of all forces acting along the incline (parallel to it), taking into account the frictional force that opposes the motion. Here’s how to calculate it step by step:

1. Resolve the Forces:

The gravitational force can be broken down into two components:

Parallel to the incline:
Perpendicular to the incline:

where:

$m$ is the mass of the object,
$g$ is the acceleration due to gravity,
$θ$ is the angle of the incline.

2. Determine the Frictional Force:

The frictional force, which opposes the motion, can be calculated using:

where $μ$ is the coefficient of friction and $F_{text{normal}}$ is the normal force, which equals $F_{text{perpendicular}}$ if there are no other vertical forces.

3. Calculate Net Force on the Incline:

The net force along the incline is the sum of all forces parallel to the incline. If we consider an upward force along the incline to be positive, the net force $F_{text{net}}$ can be calculated as:

$F_{text{net}} = F_{text{applied}} - F_{text{friction}} - F_{text{parallel}}$

Example Calculation:

Let’s calculate the net force for a 10 kg object on a 30-degree incline with an applied force of 50 N up the incline, a frictional force of 20 N, and a coefficient of friction $μ = 0.3$ .

1. Calculate the Weight Components:

$F_{text{parallel}} = 10 , text{kg} cdot 9.8 , text{m/s}^2 cdot sin(30^circ)$

$F_{text{perpendicular}} = 10 , text{kg} cdot 9.8 , text{m/s}^2 cdot cos(30^circ)$

2. Calculate the Frictional Force:

$F_{text{friction}} = 0.3 cdot F_{text{perpendicular}}$

3. Calculate the Net Force:

$F_{text{net}} = 50 , text{N} - 20 , text{N} - F_{text{parallel}}$

After calculating

$F_{text{parallel}}$ and $F_{text{friction}}$ with the values obtained above, you would insert those to find $F_{text{net}}$

Determining Net Force in Circular Motion

In circular motion, an object experiences a centripetal force directed towards the center of the circular path. This force is responsible for keeping the object in its circular trajectory. By considering this centripetal force and other forces, we can determine the net force.

Formula for finding the net force in circular motion:

$F_{text{net}} = frac{mv^2}{r}$

Where:
– $F_{text{net}}$ is the net force acting on the object.
– $m$ is the mass of the object.
– $v$ is the velocity of the object.
– $r$ is the radius of the circular path.

Example:
Let’s say you have a 500-gram object moving in a circular path with a radius of 2 meters. The object has a velocity of 4 meters per second. Calculate the net force acting on the object.

Solution:
1. First, convert the mass to kilograms since the SI unit for mass is kilograms. 500 grams is equal to 0.5 kilograms.

2. Plug the values into the formula:
$F_{text{net}} = frac{(0.5, text{kg}) cdot (4, text{m/s})^2}{2, text{m}}$

3. Calculate the net force:
$F_{text{net}} = frac{0.5 , text{kg} cdot 16 , text{m}^2/text{s}^2}{2 , text{m}} = 4 , text{N}$

So, the net force acting on the object is 4 Newtons.

Calculating Net Force on a Charge

To calculate the net force on a charge, you must consider all of the forces exerted by other charges in the vicinity. This involves using Coulomb’s Law, which states that the force between two point charges is directly proportional to the product of the magnitudes of the charges and inversely proportional to the square of the distance between them. The formula is given by:

$F = k cdot frac{|q_1 cdot q_2|}{r^2}$

Where:

$F$ is the magnitude of the force between the charges,
$k$ is Coulomb’s constant ( $8.9875 times 10^9 , text{N} cdot text{m}^2/text{C}^2$ ),
$q_1$ and $q_2$ are the magnitudes of the charges,
$r$ is the distance between the centers of the two charges.

The force is attractive if the charges are of opposite signs and repulsive if the charges have the same sign.

Example: Calculating Net Force on a Charge

Imagine three point charges in space:

The first charge $Q_1$ is $+2 mu C$ at position $(0, 0)$ .
The second charge $Q_2$ is $-3 mu C$ at position $(0, 4)$ meters.
The third charge $Q_3$ is $+1 mu C$ at position $(3, 0)$ meters.

We want to calculate the net force on charge $Q_1$ .

First, calculate the force between $Q_1$ and $Q_2$ :

$F_{12} = k cdot frac{|Q_1 cdot Q_2|}{r_{12}^2}$

Substitute the known values:

$F_{12} = (8.9875 times 10^9) cdot frac{|2 times 10^{-6} cdot -3 times 10^{-6}|}{4^2}$

$F_{12} = (8.9875 times 10^9) cdot frac{6 times 10^{-12}}{16}$

$F_{12} = 3.3684375 times 10^{-3} , text{N}$

This force is attractive, so it acts along the line connecting $Q_1$ and $Q_2$ , towards $Q_2$ .

Now, calculate the force between $Q_1$ and $Q_3$ :

$F_{13} = k cdot frac{|Q_1 cdot Q_3|}{r_{13}^2}$

$F_{13} = (8.9875 times 10^9) cdot frac{|2 times 10^{-6} cdot 1 times 10^{-6}|}{3^2}$

$F_{13} = (8.9875 times 10^9) cdot frac{2 times 10^{-12}}{9}$

$F_{13} = 1.9955 times 10^{-3} , text{N}$

This force is repulsive, so it acts along the line connecting $Q_1$ and $Q_3$ , away from $Q_3$ .

The net force on $Q_1$ is the vector sum of $F_{12}$ and $F_{13}$ . Since these forces act at right angles to each other, we can use the Pythagorean theorem to find the resultant force $F_{net}$ :

$F_{net} = sqrt{F_{12}^2 + F_{13}^2}$

$F_{net} = sqrt{(3.3684375 times 10^{-3})^2 + (1.9955 times 10^{-3})^2}$

$F_{net} = sqrt{(11.3476 times 10^{-6}) + (3.9822 times 10^{-6})}$

$F_{net} = sqrt{15.3298 times 10^{-6}}$

$F_{net} = 3.915 times 10^{-3} , text{N}$

The direction of this force can be determined by the angle $θ$ it makes with the x-axis, which can be found using trigonometry:

To determine the direction of the net force on charge $( Q_1 )$ , we need to consider the forces exerted by charges $( Q_2 )$ and $( Q_3 )$ . Since $( Q_2 )$ is located above $( Q_1 ) and ( Q_3 )$ is to the right of $( Q_1 )$ , we calculate the net force direction by finding the angle ( theta ) with respect to the negative y-axis.

The force due to $( Q_2 )$ is directed vertically downward (negative y-direction), and the force due to $( Q_3 )$ is directed horizontally to the right (positive x-direction). To calculate $( theta )$ , we use the arctangent function:

$[ theta = arctanleft(frac{F_{12}}{F_{13}}right) ]$

Substitute the values of $( F_{12} ) and ( F_{13 ) to calculate ( theta )$ :

$[ theta = arctanleft(frac{3.3684375 times 10^{-3} , text{N}}{1.9955 times 10^{-3} , text{N}}right) ] [ theta approx arctan(1.687) ] [ theta approx 59.9^circ ]$

The angle $( theta )$ is measured counterclockwise from the positive x-axis and determines the direction of the net force. Since $( Q_2 )$ exerts a force downward and $( Q_3 )$ exerts a force to the right, the net force’s direction is in the fourth quadrant of the coordinate system.

Hence, the direction of the net force on charge $( Q_1 )$ is approximately $( 300.1^circ )$ counterclockwise from the positive x-axis.

Practical Applications of Net Force

The Atwood Machine and Net Force

The Atwood machine is a mechanical device that utilizes the concept of net force. It consists of a pulley, a string, and two masses. By applying Newton’s second law and considering the net force, we can analyze the motion of the masses in the Atwood machine.

Net Force in Science and Everyday Life

Net force is a crucial concept in various scientific disciplines, including physics, engineering, and astronomy. Its understanding helps us explain and predict the motion of objects in our everyday lives, such as the movement of vehicles, the behavior of sports equipment, or the flight of a ball.

The Role of Net Force in Vehicle Motion and Safety

Net force plays a vital role in understanding the motion and safety of vehicles. By considering the net force acting on a vehicle, we can analyze its acceleration, braking, and stability. This knowledge allows us to design safer vehicles and develop strategies for accident prevention.

Worked Out Examples

Example of Finding Net Force with Given Mass and Acceleration

Let’s consider an object with a mass of 5 kilograms and an acceleration of 10 meters per second squared. To find the net force acting on the object, we can use the formula $F_{text{net}} = m cdot a$ . Substituting the given values, we have $F_{text{net}} = 5 , text{kg} times 10 , text{m/s}^2 = 50 , text{N}$ . Therefore, the net force acting on the object is 50 Newtons.

Example of Calculating Net Force on an Inclined Plane

Suppose we have an object on an inclined plane with a mass of 2 kilograms. The angle of the incline is 30 degrees, and the force of friction is 5 Newtons. The force of gravity can be resolved into two components: one parallel to the plane and one perpendicular to the plane. By considering these components and subtracting the force of friction, we can calculate the net force.

Example of Determining Net Force in Circular Motion

Consider an object moving in a circular path with a radius of 3 meters and a speed of 4 meters per second. To maintain circular motion, the object experiences a centripetal force directed towards the center of the circle. By considering this centripetal force and any other applicable forces, we can determine the net force acting on the object.

Common Mistakes and Misconceptions in Finding Net Force

Image by w:File:Non-parallel net force.jpg – Wikimedia Commons, Wikimedia Commons, Licensed under CC BY-SA 3.0.

Misunderstanding of Vector Components

One common mistake is misunderstanding vector components. It is crucial to accurately break down forces into their x and y components to correctly determine the net force in different directions.

Confusion between Net Force and Individual Forces

Sometimes, students confuse net force with individual forces. Net force represents the overall effect of all the forces acting on an object, whereas individual forces act independently on the object.

Overlooking the Effects of Friction and Air Resistance

Another common mistake is overlooking the effects of friction and air resistance. These forces can significantly impact the net force acting on an object, especially when considering real-world scenarios.

Quick Facts:

Q: What should one take into account when considering the concept of Net Force?

A: When considering net force, one should take into account that it is essentially the sum of all the forces acting upon an object. It’s necessary to note that forces come from different directions and can cancel each other out if they are equal and opposite. Meanwhile, unbalanced forces will lead to a change in motion or direction according to Newton’s first law.

Q: Can you illustrate the application of net force in a given situation?

A: Sure. Let’s imagine an object at rest on the floor. It has two main forces acting upon it: the gravitational force pulling it downward and the normal force from the floor pushing it upward. If these forces balance, the object remains at rest because the total sum of all the forces is zero, which we refer to as the net force of zero.

Q: How can diagrams be useful in understanding Net Force?

A: Diagrams can effectively help us visually understand how multiple forces are acting on an object and illustrate how these forces can add up to a net force. They can demonstrate vectors showing the direction and magnitude of each force, making it clear when forces cancel each other out or create an unbalanced, net force.

Q: What is the role of friction force in the account of net force?

A: Friction force always acts in the opposite direction of an object’s motion. If you push an object on a surface, the friction force from the surface is trying to resist or slow down this motion. Therefore, in calculating the net force, you need to count the friction force as a negative force if your push force is considered positive.

Q: What’s the standard unit of measurement for net force?

A: The standard unit of measurement for net force is the Newton (N). For example, if a 20 N force is acting to the right, and a 20 N force is also acting to the left, the net force would be 0 N because they cancel each other out.

Q: What happens when the net force is zero?

A: When the net force is zero, it means that all the forces acting on an object are balanced. As per Newton’s First Law, an object at rest tends to stay at rest, and an object in motion tends to stay in motion with the same speed and in the same direction unless acted upon by an unbalanced force. So, if the net force is zero, an object will maintain its state of motion.

How can the concepts of finding net force and calculating net force using mass and speed be combined?

The intersection between finding net force and calculating net force using mass and speed is a crucial aspect in understanding the physical forces involved in different scenarios. By considering the mass and speed of an object, the net force acting upon it can be determined. To explore this further, check out the article on “Calculating net force using mass and speed”.

Q: How can I calculate net force in a given situation?

A: To calculate net force in any given situation, you need to understand the direction and magnitude of each force acting upon an object. You add all the forces that are acting in the same direction and consider those in the opposite direction as negative. For constant forces, the net force is the sum of all these forces.

Also Read:

How to Calculate Tension Between Two Objects: A Comprehensive Guide

June 18, 2024October 13, 2021 by Keerthi Murthi

Calculating the tension between two objects is a fundamental concept in physics, particularly in the study of mechanics and statics. This comprehensive guide will provide you with a deep understanding of the principles, formulas, and practical applications involved in determining the tension between two objects.

Understanding Tension and Its Importance

Tension is a force that acts along the length of a rope, string, or cable, and it is responsible for supporting the weight of an object or maintaining the equilibrium of a system. Accurately calculating tension is crucial in various engineering applications, such as the design of structures, the analysis of mechanical systems, and the study of forces in everyday life.

Fundamental Principles and Equations

To calculate the tension between two objects, we need to apply the principles of Newton’s laws of motion, specifically Newton’s second law, which states that the net force acting on an object is equal to its mass multiplied by its acceleration.

The general equation for calculating tension is:

T = mg + ma

Where:
– T is the tension force
– m is the mass of the object
– g is the acceleration due to gravity (9.8 m/s²)
– a is the acceleration of the object

Free Body Diagrams and Force Analysis

One of the key steps in calculating tension is to draw a free body diagram (FBD) of the system. The FBD represents all the forces acting on the object, including the tension force, the force of gravity, and any other external forces.

By analyzing the FBD and applying Newton’s second law, you can set up a system of equations to solve for the unknown tension force. This process involves breaking down the forces into their horizontal and vertical components and using the equations of equilibrium to find the tension.

Example 1: Tension in a Hanging Object

Consider a scenario where a 5 kg object is suspended from a rope. To calculate the tension in the rope, we can follow these steps:

Draw the free body diagram of the object.
Identify the known and unknown forces acting on the object.
Known forces: Weight of the object (mg)
Unknown force: Tension in the rope (T)
Apply Newton’s second law in the vertical direction:
Σ Fy = ma T - mg = 0 T = mg T = (5 kg) × (9.8 m/s²) = 49 N
The tension in the rope is 49 N.

Example 2: Tension in a Pulley System

Now, let’s consider a more complex system involving a pulley. Suppose a 10 kg object is suspended from a rope that passes over a frictionless pulley, and the other end of the rope is attached to a 5 kg object.

Draw the free body diagram of the system.
Identify the known and unknown forces acting on each object.
Known forces: Weight of the 10 kg object (10 × 9.8 = 98 N), Weight of the 5 kg object (5 × 9.8 = 49 N)
Unknown force: Tension in the rope (T)
Apply Newton’s second law to the 10 kg object in the vertical direction:
Σ Fy = ma T - 98 = 0 T = 98 N
Apply Newton’s second law to the 5 kg object in the vertical direction:
Σ Fy = ma T - 49 = 0 T = 49 N
The tension in the rope is 98 N on the side of the 10 kg object and 49 N on the side of the 5 kg object.

Advanced Concepts and Applications

Tension in Inclined Planes

When an object is placed on an inclined plane, the tension in the supporting rope or cable can be calculated by considering the components of the weight force along the inclined surface.

Tension in Rotating Systems

For objects undergoing circular motion, the tension force must account for the centripetal force acting on the object, which is proportional to the mass, velocity, and radius of the circular path.

Tension in Elastic Materials

In the case of elastic materials, such as springs or cables, the tension force is related to the deformation of the material and its elastic properties, which can be described by Hooke’s law.

Tension in Fluid Dynamics

In the study of fluid mechanics, the concept of tension is important in the analysis of surface tension, capillary action, and the behavior of fluids in narrow channels or porous media.

Numerical Problems and Practice

To solidify your understanding of calculating tension between two objects, it is essential to practice solving numerical problems. Here are a few examples:

A 2 kg object is suspended from a rope. Calculate the tension in the rope.
A 5 kg object is attached to one end of a rope, and the other end is pulled with a force of 20 N. Calculate the tension in the rope.
A 10 kg object is placed on an inclined plane with an angle of 30 degrees. Calculate the tension in the supporting rope.
A 3 kg object is attached to a spring with a spring constant of 500 N/m. Calculate the tension in the spring when the object is displaced by 0.1 m.

By working through these problems and understanding the underlying principles, you will develop the skills necessary to calculate tension in a wide range of physical systems.

Conclusion

Calculating the tension between two objects is a fundamental skill in physics and engineering. By mastering the concepts, equations, and problem-solving techniques presented in this guide, you will be well-equipped to tackle a variety of tension-related problems in your studies and future career.

Remember, the key to success in this field is a deep understanding of the underlying principles, the ability to apply them in different scenarios, and a commitment to continuous learning and practice.

Reference:

How to Calculate Tension in a String: A Comprehensive Guide

June 18, 2024October 11, 2021 by Keerthi Murthi

Calculating the tension in a string is a fundamental concept in physics, engineering, and music. The tension in a string is a crucial parameter that determines the behavior and performance of various systems, from musical instruments to mechanical structures. In this comprehensive guide, we will delve into the details of how to calculate the tension in a string, providing you with a thorough understanding of the underlying principles and practical applications.

Understanding the Tension Formula

The formula used to calculate the tension in a string is derived from the wave equation and is given by:

T = (2 * π^2 * f^2 * m) / L

Where:
– T is the tension in the string, measured in Newtons (N) or pounds-force (lbf)
– f is the frequency of vibration, measured in Hertz (Hz)
– m is the mass per unit length (linear density) of the string, measured in kilograms per meter (kg/m) or pounds per foot (lb/ft)
– L is the length of the vibrating section of the string, measured in meters (m) or feet (ft)

This formula is based on the principle of wave propagation in a string, where the tension in the string is directly related to the frequency of vibration, the linear density of the string, and the length of the vibrating section.

Calculating Tension: Step-by-Step Approach

To calculate the tension in a string, follow these steps:

Determine the Frequency of Vibration (f): The frequency of vibration is the number of complete oscillations or cycles per unit of time, typically measured in Hertz (Hz). For musical instruments, the frequency of vibration can be determined by the pitch of the string.
Measure the Linear Density (m): The linear density, or mass per unit length, of the string is a crucial parameter in the tension calculation. This value can be obtained from the manufacturer’s specifications or by directly measuring the mass and length of the string.
Measure the Length of the Vibrating Section (L): The length of the vibrating section of the string is the distance between the two fixed points or supports, such as the bridge and the nut of a guitar.
Substitute the Values into the Tension Formula: Once you have the values for frequency, linear density, and length, you can substitute them into the tension formula and calculate the tension in the string.

T = (2 * π^2 * f^2 * m) / L

Here’s an example calculation for a guitar string:
– Frequency (f) = 330 Hz
– Linear Density (m) = 0.004 kg/m
– Length of Vibrating Section (L) = 0.66 m
– Tension (T) = (2 * π^2 * 330^2 * 0.004) / 0.66 ≈ 115.5 N or 25.9 lbf

This means that the tension in the guitar string is approximately 115.5 Newtons or 25.9 pounds-force.

Factors Affecting String Tension

Several factors can influence the tension in a string, including:

Material and Thickness: The material and thickness of the string affect its linear density and, consequently, the tension.
Tuning: The tuning of the string, which is determined by the frequency of vibration, directly impacts the tension.
Length of the Vibrating Section: The length of the vibrating section of the string, which is determined by the instrument’s design, affects the tension.
Environmental Conditions: Changes in temperature and humidity can cause the string to expand or contract, affecting its tension.

Understanding these factors is crucial when designing, maintaining, or troubleshooting systems that involve strings, such as musical instruments, tensioned cables, and mechanical systems.

Measuring String Tension

In addition to calculating the tension using the formula, you can also measure the tension in a string directly using a string tension gauge. A string tension gauge is a device that measures the force required to stretch the string by a certain distance.

To use a string tension gauge, follow these steps:

Choose the Appropriate Gauge: Select a string tension gauge that is suitable for your string type and gauge. There are various types of string tension gauges available, including digital, mechanical, and analog models.
Attach the Gauge to the String: Insert the hook or clamp of the gauge into the string and adjust the position of the gauge so that it is parallel to the string and does not touch any other part of the instrument.
Measure the Tension: Gently pull the string with the gauge and read the force value displayed on the gauge. The force value is typically measured in pounds (lbs), kilograms (kg), or newtons (N).
Compare to the Desired Tension: Compare the measured tension value with the desired or recommended tension value for the string. You can find the recommended tension value in the specifications of the string or the instrument, or you can calculate it using the formula above.
Adjust the Tension: If necessary, adjust the tension of the string by either tightening or loosening it until it reaches the desired or recommended tension value.

Measuring the tension in a string accurately and consistently is crucial for ensuring the optimal performance and longevity of the string and the instrument.

Advanced Considerations

For more advanced applications, there are additional factors and considerations to take into account when calculating the tension in a string:

Nonlinear Behavior: The tension formula assumes that the string is under small tension and vibrates in a plane. In some cases, the string may exhibit nonlinear behavior, which requires more complex models and analysis.
Damping and Energy Dissipation: The presence of damping and energy dissipation in the string can affect the tension and the overall behavior of the system.
Coupling and Interactions: In complex systems, the tension in a string may be influenced by its coupling and interactions with other components, such as the instrument’s body or other strings.
Numerical Simulations: For more accurate and detailed analysis, numerical simulations using finite element methods or other computational techniques can be employed to model the behavior of strings under various conditions.

These advanced considerations are typically explored in specialized fields, such as musical acoustics, structural engineering, and computational physics.

Conclusion

Calculating the tension in a string is a fundamental skill in physics, engineering, and music. By understanding the tension formula, the factors that affect string tension, and the methods for measuring tension, you can gain a deeper understanding of the behavior and performance of various systems that involve strings.

Whether you’re working with musical instruments, tensioned cables, or mechanical systems, mastering the techniques presented in this guide will equip you with the knowledge and tools necessary to analyze, design, and troubleshoot string-based systems effectively.

References

String Tension Formula and Calculator – Liutaio Mottola
https://www.liutaiomottola.com/formulae/tension.htm
Tension (Physics): Definition, Formula, How to Find (w/ Diagrams & Examples) – Sciencing
https://sciencing.com/tension-physics-definition-formula-how-to-find-w-diagrams-examples-13720451.html
Calculating the Tension in the Strings – Physics Ninja (YouTube)
https://www.youtube.com/watch?v=UaBPwH3_odU
Guitar String Tension Calculator – Omnicalculator
https://www.omnicalculator.com/other/guitar-string-tension
How to measure string tension easily – PR Gomez
https://prgomez.com/how-to-measure-string-tension-easily/

How to Calculate Projectile Motion: A Comprehensive Guide

June 18, 2024September 26, 2021 by Alpa P. Rajai

Projectile motion is a fundamental concept in physics that describes the motion of an object that is launched into the air and subjected to the constant acceleration of gravity. To accurately calculate various aspects of projectile motion, such as the time of flight, range, and maximum height, you can use a set of equations derived from the principles of kinematics and the constant acceleration due to gravity.

Understanding the Equations of Projectile Motion

The key equations used to calculate projectile motion are as follows:

Horizontal Velocity Component (Vx):
Equation: Vx = V₀ cos(α)
Where:
- Vx is the horizontal velocity component
- V₀ is the initial velocity
- α is the launch angle
Vertical Velocity Component (Vy):
Equation: Vy = V₀ sin(α) – gt
Where:
- Vy is the vertical velocity component
- V₀ is the initial velocity
- α is the launch angle
- g is the acceleration due to gravity (9.8 m/s²)
- t is the time
Time of Flight (t):
If the initial height (h) is 0:
- Equation: t = 2Vy₀/g
If the initial height (h) is greater than 0:
- Equation: t = [Vy₀ + √(Vy₀²+ 2gh)]/g
Range of the Projectile (R):
If the initial height (h) is 0:
- Equation: R = 2VxVy₀/g
If the initial height (h) is greater than 0:
- Equation: R = Vx[Vy₀ + √(Vy₀²+ 2gh)]/g
Maximum Height (hmax):
If the initial height (h) is 0:
- Equation: hmax = Vy₀²/(2g)
If the initial height (h) is greater than 0:
- Equation: hmax = h + Vy₀²/(2g)

In these equations, the following variables are used:
– V₀: Initial velocity
– α: Launch angle
– g: Acceleration due to gravity (9.8 m/s²)
– t: Time
– h: Initial height
– Vx: Horizontal velocity component
– Vy: Vertical velocity component
– R: Range of the projectile
– hmax: Maximum height of the projectile

Understanding Vectors and Right Triangles

To calculate the horizontal and vertical velocity components, it is essential to understand the concepts of vectors and right triangles. The initial velocity (V₀) can be represented as a vector, and the horizontal and vertical components can be determined using trigonometric functions.

The horizontal velocity component (Vx) is equal to the initial velocity (V₀) multiplied by the cosine of the launch angle (α):
– Vx = V₀ cos(α)

The vertical velocity component (Vy) is equal to the initial velocity (V₀) multiplied by the sine of the launch angle (α), minus the product of the acceleration due to gravity (g) and the time (t):
– Vy = V₀ sin(α) – gt

By understanding these vector relationships and applying the appropriate trigonometric functions, you can accurately calculate the horizontal and vertical velocity components.

Practical Examples and Numerical Problems

To better understand the application of these equations, let’s consider some practical examples and numerical problems.

Example 1: Projectile Launched from Ground Level
Suppose a projectile is launched from ground level (h = 0) with an initial velocity of 50 m/s and a launch angle of 30 degrees. Calculate the time of flight, range, and maximum height of the projectile.

Given:
– V₀ = 50 m/s
– α = 30 degrees
– h = 0

Step 1: Calculate the horizontal velocity component (Vx).
Vx = V₀ cos(α)
Vx = 50 m/s × cos(30°) = 43.30 m/s

Step 2: Calculate the vertical velocity component (Vy).
Vy = V₀ sin(α) – gt
Vy = 50 m/s × sin(30°) – (9.8 m/s²) × t

Step 3: Calculate the time of flight (t).
Since the initial height (h) is 0, the time of flight is given by:
t = 2Vy₀/g
t = 2 × (50 m/s × sin(30°)) / 9.8 m/s² = 2.04 s

Step 4: Calculate the range (R).
Since the initial height (h) is 0, the range is given by:
R = 2VxVy₀/g
R = 2 × (43.30 m/s) × (50 m/s × sin(30°)) / 9.8 m/s² = 86.60 m

Step 5: Calculate the maximum height (hmax).
Since the initial height (h) is 0, the maximum height is given by:
hmax = Vy₀²/(2g)
hmax = (50 m/s × sin(30°))²/(2 × 9.8 m/s²) = 31.63 m

Example 2: Projectile Launched from a Non-Zero Initial Height
Suppose a projectile is launched from a height of 5 meters with an initial velocity of 60 m/s and a launch angle of 45 degrees. Calculate the time of flight, range, and maximum height of the projectile.

Given:
– V₀ = 60 m/s
– α = 45 degrees
– h = 5 m

Step 1: Calculate the horizontal velocity component (Vx).
Vx = V₀ cos(α)
Vx = 60 m/s × cos(45°) = 42.43 m/s

Step 2: Calculate the vertical velocity component (Vy).
Vy = V₀ sin(α) – gt
Vy = 60 m/s × sin(45°) – (9.8 m/s²) × t

Step 3: Calculate the time of flight (t).
Since the initial height (h) is greater than 0, the time of flight is given by:
t = [Vy₀ + √(Vy₀²+ 2gh)]/g
t = [60 m/s × sin(45°) + √((60 m/s × sin(45°))² + 2 × 9.8 m/s² × 5 m)]/9.8 m/s² = 4.24 s

Step 4: Calculate the range (R).
Since the initial height (h) is greater than 0, the range is given by:
R = Vx[Vy₀ + √(Vy₀²+ 2gh)]/g
R = (42.43 m/s) × [60 m/s × sin(45°) + √((60 m/s × sin(45°))² + 2 × 9.8 m/s² × 5 m)]/9.8 m/s² = 120.00 m

Step 5: Calculate the maximum height (hmax).
Since the initial height (h) is greater than 0, the maximum height is given by:
hmax = h + Vy₀²/(2g)
hmax = 5 m + (60 m/s × sin(45°))²/(2 × 9.8 m/s²) = 35.63 m

These examples demonstrate the application of the projectile motion equations and the importance of considering the initial height in the calculations.

Additional Considerations and Factors

When calculating projectile motion, there are a few additional factors and considerations to keep in mind:

Air Resistance: In real-world scenarios, air resistance can have a significant impact on the motion of a projectile. The equations presented in this guide assume negligible air resistance, but in some cases, it may be necessary to incorporate air resistance into the calculations.
Angle of Elevation: The angle of elevation, which is the angle between the horizontal and the line of sight to the target, can also affect the projectile’s trajectory and range.
Coriolis Effect: For long-range projectiles, the Coriolis effect, which is the apparent deflection of moving objects due to the Earth’s rotation, may need to be considered.
Projectile Shape and Drag Coefficient: The shape and aerodynamic properties of the projectile can influence its motion, and the drag coefficient should be taken into account for more accurate calculations.
Environmental Factors: Factors such as wind, temperature, and humidity can also affect the projectile’s motion and should be considered in certain applications.

By understanding these additional factors and incorporating them into the calculations, you can further refine your understanding of projectile motion and improve the accuracy of your predictions.

Conclusion

Calculating projectile motion is a fundamental skill in physics and can be applied in various fields, from ballistics and sports to engineering and astronomy. By mastering the equations and concepts presented in this guide, you can accurately determine the time of flight, range, and maximum height of a projectile, given the initial conditions.

Remember to always consider the initial height, understand the relationships between vectors and right triangles, and be aware of any additional factors that may influence the projectile’s motion. With practice and a solid understanding of the underlying principles, you can become proficient in calculating projectile motion and apply these skills to a wide range of real-world scenarios.

References

Projectile Motion – University Physics Volume 1, https://pressbooks.bccampus.ca/universityphysicssandbox/chapter/projectile-motion/
Projectile Motion Calculator, https://www.omnicalculator.com/physics/projectile-motion
Physics 223 General Physics Lab Experiment 5: Projectile Motion, https://www.phy.olemiss.edu/lab/LabPDFs/223/LabManual/5_ProjectileMotion_223/TAP_Projectiles_223.pdf
Projectile Motion: Equations and Examples, https://www.thoughtco.com/projectile-motion-equations-2698949
Projectile Motion: Theory and Examples, https://www.physicsclassroom.com/class/vectors/Lesson-4/Projectile-Motion-Theory-and-Examples

How to Calculate Instantaneous Velocity Formula

June 18, 2024August 9, 2021 by Raghavi Acharya

The instantaneous velocity formula is a fundamental concept in physics that describes the velocity of an object at a specific moment in time. It is the derivative of the position function with respect to time, which represents the rate of change of an object’s position over an infinitesimally small interval. Understanding and applying the instantaneous velocity formula is crucial for analyzing the motion of objects in various fields, including mechanics, engineering, and even biology.

Understanding Instantaneous Velocity

Instantaneous velocity is the velocity of an object at a specific moment in time, as opposed to the average velocity, which is the change in position divided by the change in time over a finite interval. Instantaneous velocity is the limit of the average velocity as the time interval approaches zero.

Mathematically, the instantaneous velocity, v(t), is defined as the derivative of the position function, x(t), with respect to time:

v(t) = dx/dt

This formula represents the rate of change of the object’s position at a specific time t. By taking the derivative of the position function, we can determine the instantaneous velocity of the object at any given moment.

Calculating Instantaneous Velocity

To calculate the instantaneous velocity formula, follow these steps:

Identify the position function: Determine the function that describes the object’s position as a function of time, x(t).
Take the derivative of the position function: Differentiate the position function with respect to time to obtain the instantaneous velocity formula, v(t) = dx/dt.
Evaluate the formula at the desired time: Substitute the specific time value t into the instantaneous velocity formula to find the velocity at that moment.

Let’s consider an example to illustrate the process:

Suppose an object’s position is given by the function x(t) = 3t^2 + 2t + 1, where t is the time in seconds and x is the position in meters.

The position function is x(t) = 3t^2 + 2t + 1.
To find the instantaneous velocity formula, we take the derivative of the position function with respect to time:
v(t) = dx/dt = 6t + 2
To find the instantaneous velocity at a specific time, say t = 2 seconds, we substitute t = 2 into the formula:
v(2) = 6(2) + 2 = 14 m/s

Therefore, the instantaneous velocity of the object at t = 2 seconds is 14 m/s.

Practical Applications of Instantaneous Velocity

The instantaneous velocity formula has numerous applications in various fields:

Mechanics: In the study of motion, the instantaneous velocity formula is used to analyze the movement of objects, such as projectiles, vehicles, and celestial bodies.
Engineering: Engineers use the instantaneous velocity formula to design and optimize the performance of mechanical systems, such as engines, robots, and transportation systems.
Biology: Biologists use the instantaneous velocity formula to study the movement of organisms, such as the locomotion of animals or the transport of molecules within cells.
Aerospace: In the aerospace industry, the instantaneous velocity formula is crucial for understanding the motion of aircraft, spacecraft, and satellites, which is essential for navigation, control, and trajectory planning.
Finance: In the financial domain, the instantaneous velocity formula can be applied to analyze the rate of change in stock prices, currency exchange rates, and other financial variables.

Advanced Concepts and Numerical Examples

To further enhance your understanding of the instantaneous velocity formula, let’s explore some advanced concepts and numerical examples:

Theorem: Instantaneous Velocity as the Derivative of Position

The instantaneous velocity formula, v(t) = dx/dt, can be derived from the fundamental theorem of calculus, which states that the derivative of a function is the limit of the average rate of change as the time interval approaches zero.

Mathematically, the instantaneous velocity can be expressed as:

v(t) = lim(Δt→0) (x(t + Δt) - x(t)) / Δt

where Δt represents the infinitesimally small time interval.

Numerical Example 1: Motion with Constant Acceleration

Consider an object with a position function x(t) = 1/2 * a * t^2 + v_0 * t + x_0, where a is the constant acceleration, v_0 is the initial velocity, and x_0 is the initial position.

To find the instantaneous velocity formula, we take the derivative of the position function:

v(t) = dx/dt = a * t + v_0

For example, if a = 2 m/s^2, v_0 = 3 m/s, and x_0 = 1 m, the instantaneous velocity formula becomes:

v(t) = 2t + 3 m/s

Numerical Example 2: Motion with Sinusoidal Position

Suppose an object’s position is described by the function x(t) = A * sin(ω * t + φ), where A is the amplitude, ω is the angular frequency, and φ is the phase shift.

To find the instantaneous velocity formula, we take the derivative of the position function:

v(t) = dx/dt = A * ω * cos(ω * t + φ)

For instance, if A = 5 m, ω = 2π rad/s, and φ = π/4 rad, the instantaneous velocity formula becomes:

v(t) = 10π * cos(2πt + π/4) m/s

Numerical Example 3: Motion with Exponential Position

Consider an object with a position function x(t) = A * e^(k * t), where A is the initial position, and k is the growth rate.

To find the instantaneous velocity formula, we take the derivative of the position function:

v(t) = dx/dt = A * k * e^(k * t)

For example, if A = 2 m and k = 0.5 s^-1, the instantaneous velocity formula becomes:

v(t) = A * k * e^(k * t) = 1 * e^(0.5t) m/s

These numerical examples demonstrate the application of the instantaneous velocity formula in various types of motion, highlighting the importance of understanding the underlying position functions and their derivatives.

Conclusion

The instantaneous velocity formula is a fundamental concept in physics that describes the velocity of an object at a specific moment in time. By understanding the derivation of this formula and applying it to various scenarios, you can gain valuable insights into the motion of objects in a wide range of applications, from mechanics and engineering to biology and finance.

Remember, the key to mastering the instantaneous velocity formula is to practice applying it to different position functions and scenarios, as well as to develop a deep understanding of the underlying principles and theorems that govern this concept.

References

University Physics Volume 1. 3.2 Instantaneous Velocity and Speed. https://courses.lumenlearning.com/suny-osuniversityphysics/chapter/3-2-instantaneous-velocity-and-speed/
Measurement of Instantaneous Velocity Vectors of Organelle Transport. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC2527267/
Science Ready. Instantaneous and Average Velocity – HSC Physics. https://scienceready.com.au/pages/instantaneous-and-average-velocity
wikiHow. How to Calculate Instantaneous Velocity. https://www.wikihow.com/Calculate-Instantaneous-Velocity
Integral Physics. Calculate Average & Instantaneous Velocity From a Position Function. https://www.youtube.com/watch?v=krtqLXsylXs