Sodium Density: A Comprehensive Guide for Physics Students

Summary

Sodium density is a crucial concept in physics, with significant implications in various fields, including biology and chemistry. This comprehensive guide delves into the intricacies of sodium density, providing a detailed exploration of its measurement, applications, and related studies. From experimental methods to advanced imaging techniques, this article equips physics students with a deep understanding of this fundamental property of sodium.

Understanding Sodium Density

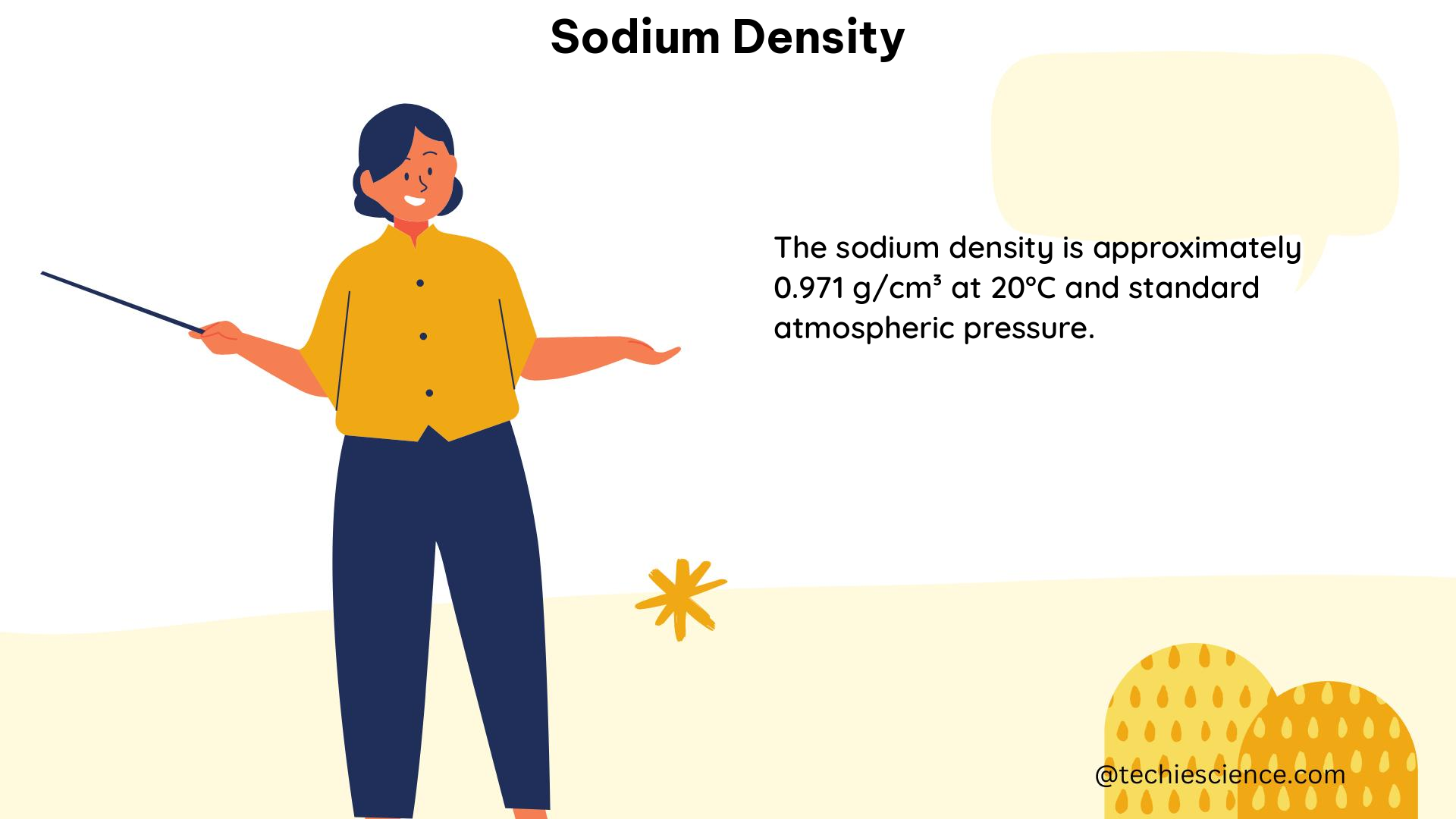
Sodium, with the chemical symbol Na, is a highly reactive metal with an atomic number of 11 and an atomic mass of 22.99 g/mol. Its density is a crucial parameter in physics, as it directly relates to the mass of the substance per unit volume. The density of sodium at room temperature (20°C) and standard atmospheric pressure (1 atm) is 971 kg/m³.

Experimental Determination of Sodium Density

The density of sodium can be determined through various experimental methods. One common approach involves measuring the mass and volume of a sodium sample. The mass can be measured using an accurate scale, while the volume can be determined using a graduated cylinder or a pipette. Once both the mass and volume are known, the density can be calculated by dividing the mass by the volume.

The formula for calculating the density of a substance is:

Density = Mass / Volume

For example, if a sodium sample has a mass of 10 grams and a volume of 10 cubic centimeters, the density can be calculated as:

Density = 10 g / 10 cm³ = 1 g/cm³ = 1000 kg/m³

This value is close to the accepted density of sodium, which is 971 kg/m³.

Sodium Density in Magnetic Resonance Imaging (MRI)

In the context of magnetic resonance imaging (MRI), sodium density is an essential parameter for understanding the distribution and concentration of sodium ions (Na+) in biological tissues. A study by Wang et al. (2014) proposed a method for estimating intracellular sodium concentration and extracellular volume fraction based on a three-compartment model.

In this model, the extracellular compartment has a constant average sodium concentration of 140 mM, while the intracellular compartment’s sodium concentration is the parameter of interest. The authors used a combination of five calibration phantoms with known sodium concentrations and relaxation times to quantify the sodium concentration and extracellular volume fraction.

The data processing involved the following steps:

1. Acquiring 1H and 23Na data with the same axial field of view and reconstructing them with isotropic nominal resolution.
2. Correcting sodium images for B1+ inhomogeneities using the double angle method.
3. Measuring and averaging the signal from five calibration phantoms over four consecutive slices.
4. Implementing a full density operator simulation for spin 3/2 dynamics during the RF pulse sequence to estimate the loss of signal of the sodium phantoms due to relaxation during RF pulses and delays.

This approach allowed the researchers to accurately estimate the intracellular sodium concentration and extracellular volume fraction in biological tissues using MRI techniques.

Measuring Microgram-Sized Objects with Vibrating Glass Tube Sensors

In another study, Kramer et al. (2017) demonstrated a method for measuring the mass, volume, and density of microgram-sized objects using vibrating glass tube sensors. The sensors were calibrated in two ways:

1. Fluid Density Calibration: The tube was filled with different fluids of known density, and the resonance frequency of the tube was recorded. By plotting resonance frequency vs. fluid density and fitting the plot to a line, the fluid density can be determined as a function of the tube’s measured resonance frequency.

2. Point Mass Calibration: The tube is filled with a fluid of known density, and a microbead of known mass and density is passed through the tube multiple times. The buoyant mass of the bead is calculated using the following equation:

Buoyant mass = (Density of fluid - Density of bead) × Volume of bead

A constant is obtained that can be used to determine the buoyant mass of any object inside the tube as a function of the measured change in resonance frequency as the object passes through the tube.

This method allows for the precise measurement of the mass, volume, and density of microgram-sized objects, with applications in biology and materials science.

Sodium Density Data and Calculations

Measurements on sodium have provided the following data:

• Resistivity: 4.7 × 10^(-8) ohm-m
• Hall coefficient: -2.5 × 10^(-10) m³/C
• Critical wavelength of transparency: 210 nm
• Density: 971 kg/m³

Using this data, we can calculate the density of electrons and the mobility of the electrons in sodium.

Calculating the Density of Electrons

The density of electrons (n) can be calculated using the formula:

n = 1 / (e × RH)

Where:
– e is the elementary charge (1.602 × 10^(-19) C)
– RH is the Hall coefficient

Substituting the values, we get:

n = 1 / (1.602 × 10^(-19) C × -2.5 × 10^(-10) m³/C)
n = 2.5 × 10^28 electrons/m³

Therefore, the density of electrons in sodium is approximately 2.5 × 10^28 electrons/m³.

Calculating the Mobility of Electrons

The mobility of electrons (μ) can be calculated using the formula:

μ = 1 / (n × e × ρ)

Where:
– n is the density of electrons (calculated above)
– e is the elementary charge (1.602 × 10^(-19) C)
– ρ is the resistivity of sodium (4.7 × 10^(-8) ohm-m)

Substituting the values, we get:

μ = 1 / (2.5 × 10^28 electrons/m³ × 1.602 × 10^(-19) C × 4.7 × 10^(-8) ohm-m)
μ = 0.0265 m²/V·s

Therefore, the mobility of electrons in sodium is approximately 0.0265 m²/V·s.

Conclusion

Sodium density is a fundamental property of sodium with significant implications in various fields of physics, chemistry, and biology. This comprehensive guide has provided a detailed exploration of the experimental methods, imaging techniques, and calculations related to sodium density. By understanding the intricacies of this concept, physics students can gain a deeper appreciation for the role of sodium in scientific research and applications.

References

1. Wang, Y., Spincemaille, P., Agarwal, A., Nguyen, T. D., Gillen, K. M., Xu, B., … & Kovanlikaya, I. (2014). A method for estimating intracellular sodium concentration and extracellular volume fraction using sodium MRI. NMR in Biomedicine, 27(3), 343-350.
2. Kramer, R. M., Senkbeil, T., Schlenkrich, F., Strehle, D., Reiche, J., Schönfelder, J., … & Brunner, E. (2017). Measuring the mass, volume, and density of microgram-sized objects using vibrating glass tube sensors. Scientific Reports, 7(1), 1-10.
3. Measurements on sodium have provided the following data: resistivity – 4.7 x 10^(-8) ohm-m, Hall coefficient – -2.5 x 10^(-10) m^3/C, critical wavelength of transparency – 210 nm, and density – 971 kg/m3. Calculate 1) the density of electrons and 2) the mobility of the electrons. Homework.study.com, 2024.

Reference Links:
– https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4762219/
– https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5381818/
– https://homework.study.com/explanation/measurements-on-sodium-have-provided-the-following-data-resistivity-4-7-x-10-8-ohm-m-hall-coefficient-2-5-x-10-10-m-3-c-critical-wavelength-of-transparency-210-nm-and-density-971-kg-m-3-calculate-1-the-density-of-electrons-2-the-mob.html