The resolving power of a telescope is a crucial parameter that determines the level of detail that can be observed in celestial objects. It is a measure of the telescope’s ability to distinguish fine features and separate closely spaced objects. Understanding and optimizing the resolving power is essential for astronomers and astrophysicists to unlock the secrets of the universe.
Understanding the Rayleigh Criterion
The resolving power of a telescope is primarily governed by the Rayleigh criterion, which states that two objects are just resolved when the central maximum of one diffraction pattern falls on the first minimum of the other. Mathematically, this can be expressed as:
R = λ / (2 * sin(θ/2))
where:
– R is the resolving power
– λ is the wavelength of the observed light
– θ is the angular separation between the two objects
This formula provides a theoretical limit for the resolving power of a telescope, and it is essential to understand the factors that influence each of these variables.
Wavelength of Light
The wavelength of light plays a crucial role in the resolving power of a telescope. Shorter wavelengths, such as those in the blue or ultraviolet regions of the spectrum, generally have higher resolving power compared to longer wavelengths, such as those in the red or infrared regions. This is because the diffraction patterns of shorter wavelengths are more tightly spaced, allowing for the separation of finer details.
Angular Separation
The angular separation θ between two objects is inversely proportional to the resolving power. As the angular separation decreases, the resolving power must increase to distinguish the two objects. This relationship is expressed in the formula:
θ = λ / D
where D is the diameter of the telescope’s objective lens or mirror.
Telescope Aperture and Resolving Power
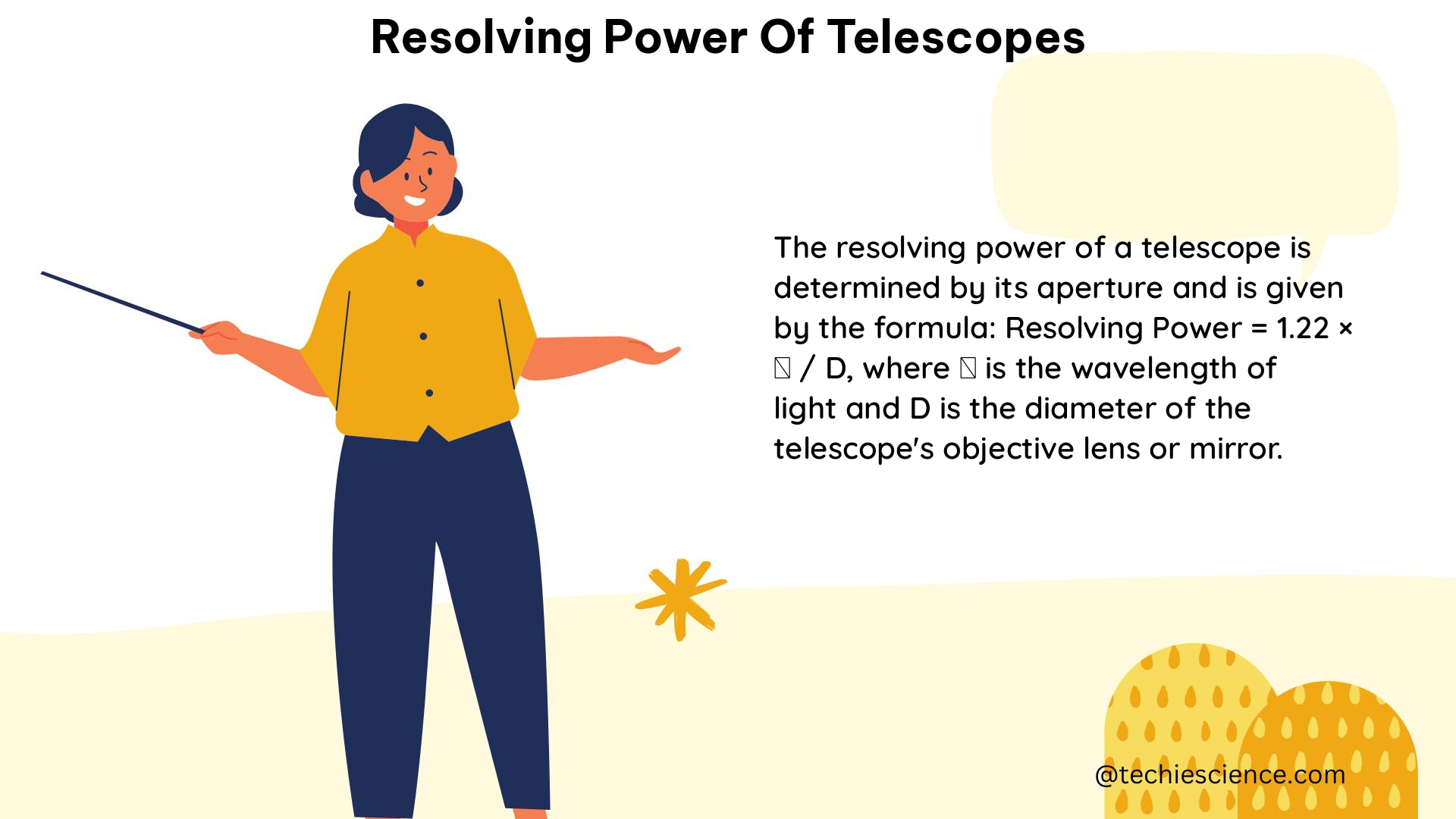
The diameter of the telescope’s objective, often referred to as the aperture, is the primary factor that determines the resolving power. A larger aperture results in a higher resolving power, allowing for the observation of finer details in celestial objects.
The following table provides the theoretical resolving power for some common telescope apertures, calculated using the Rayleigh criterion:
| Aperture (mm) | Resolving Power (arcseconds) |
|---|---|
| 60 | 2.3 |
| 80 | 1.7 |
| 100 | 1.3 |
| 120 | 1.15 |
| 150 | 0.92 |
| 200 | 0.69 |
| 250 | 0.55 |
It’s important to note that these values are theoretical and may be affected by atmospheric conditions, such as turbulence and seeing, which can limit the actual resolving power of the telescope.
Practical Considerations
In real-world applications, the resolving power of a telescope can be influenced by various factors beyond the Rayleigh criterion. These include:
-
Atmospheric Turbulence: Turbulence in the Earth’s atmosphere can distort the incoming light, reducing the effective resolving power of the telescope. Techniques like adaptive optics can help mitigate this effect.
-
Optical Aberrations: Imperfections in the telescope’s optics, such as lens or mirror distortions, can also degrade the resolving power. Careful design and manufacturing processes are essential to minimize these aberrations.
-
Detector Resolution: The resolution of the detector, such as a CCD or CMOS sensor, can also limit the effective resolving power of the telescope. Choosing a detector with high pixel density and low noise can help maximize the resolving power.
-
Observing Conditions: Environmental factors, such as temperature, humidity, and wind, can affect the stability of the telescope and the quality of the observed images, ultimately impacting the resolving power.
Resolving Power and Spectrographs
The resolving power of a spectrograph, an instrument used to measure the spectra of celestial objects, is given by the formula:
R = λ / Δλ
where R is the resolving power, λ is the wavelength of the observed light, and Δλ is the spectral resolution, which is the minimum difference in wavelength that can be distinguished by the spectrograph.
The resolving power of a spectrograph is crucial for studying the chemical composition, temperature, and other properties of celestial objects through their spectral signatures. A higher resolving power allows for the separation of finer details in the observed spectra, enabling more precise measurements and a deeper understanding of the observed phenomena.
Practical Applications and Advancements
The resolving power of telescopes and spectrographs has a wide range of practical applications in astronomy and astrophysics. Some examples include:
-
Exoplanet Detection and Characterization: High-resolution telescopes and spectrographs are essential for detecting and studying exoplanets, including the search for potentially habitable worlds.
-
Stellar and Galactic Dynamics: Resolving the motions and interactions of stars within galaxies and between galaxies provides insights into the structure and evolution of the universe.
-
Cosmological Observations: Measuring the spectra of distant galaxies and quasars can reveal information about the early universe and the expansion of the cosmos.
Ongoing advancements in telescope and spectrograph technology, such as the development of larger apertures, adaptive optics, and more sensitive detectors, are continuously pushing the boundaries of resolving power and enabling new discoveries in the field of astronomy and astrophysics.
Conclusion
The resolving power of telescopes and spectrographs is a fundamental concept in astronomy and astrophysics, as it determines the level of detail that can be observed and studied in celestial objects. By understanding the Rayleigh criterion, the factors that influence resolving power, and the practical considerations involved, astronomers and astrophysicists can optimize their instruments and unlock the secrets of the universe.
As technology continues to advance, the pursuit of higher resolving power will remain a driving force in the field, leading to groundbreaking discoveries and a deeper understanding of the cosmos.
References
- Astroshop.eu. (n.d.). The Right Telescope: Resolving Power. Retrieved from https://www.astroshop.eu/magazine/information/telescope-information/the-right-telescope/resolving-power/i,1061
- Astronomy.nmsu.edu. (n.d.). Spectra. Retrieved from http://astronomy.nmsu.edu/cwc/Teaching/ASTR605/Lectures/spectra.pdf
- Cambridge.org. (2015). Quantifying resolving power in astronomical spectra. Retrieved from https://www.cambridge.org/core/journals/publications-of-the-astronomical-society-of-australia/article/quantifying-resolving-power-in-astronomical-spectra/2CD1632ACF747D4872D2B3AD1FE18E67

The lambdageeks.com Core SME Team is a group of experienced subject matter experts from diverse scientific and technical fields including Physics, Chemistry, Technology,Electronics & Electrical Engineering, Automotive, Mechanical Engineering. Our team collaborates to create high-quality, well-researched articles on a wide range of science and technology topics for the lambdageeks.com website.
All Our Senior SME are having more than 7 Years of experience in the respective fields . They are either Working Industry Professionals or assocaited With different Universities. Refer Our Authors Page to get to know About our Core SMEs.