Proton Density 2: A Comprehensive Guide for Physics Students

Summary

Proton density (ρ) is a crucial parameter in Magnetic Resonance Imaging (MRI) that refers to the density of MRI-visible protons, primarily located in tissue water. Accurate measurement of proton density is essential for quantitative MRI (qMRI) as it can be compared across different instruments, subjects, and time points, eliminating instrumental bias. This comprehensive guide delves into the technical details of proton density 2, covering the underlying principles, measurement techniques, and the latest advancements in the field.

Understanding Proton Density 2

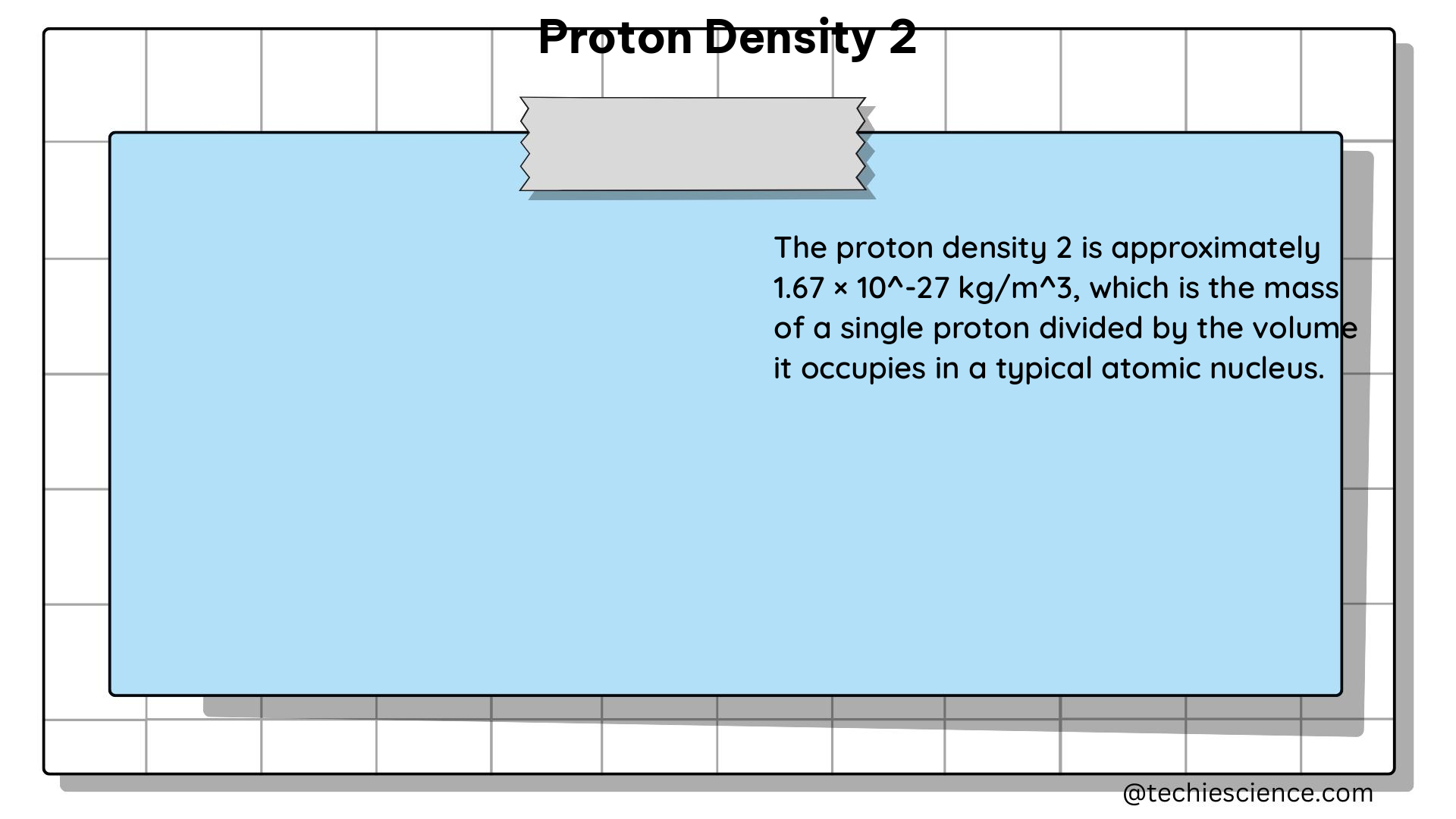
Principles of Proton Density Measurement

Proton density (ρ) is a measure of the concentration of MRI-visible protons, which are predominantly found in tissue water. The proton density is typically derived from local image intensities in a dataset acquired with high signal-to-noise ratio (SNR) and spatial resolution. However, the observed signal intensities are influenced by various secondary effects, such as:

1. Relaxation Time Weighting: The signal intensities are weighted by the longitudinal (T1) and transverse (T2*) relaxation times of the tissue.
2. Magnetic Field Distortions: Distortions in the static magnetic field (B0) and the transmitted radio-frequency (RF) field (B1) can also affect the signal intensities.

To obtain a pure ρ-weighted image, these secondary effects must be corrected. This is achieved through a series of sub-experiments that map the relevant parameters, such as T1, T2*, and B1.

Proton Density Quantification

The corrected image intensities yield a Multiplication Factor (MF) map, which is the product of the actual ρ-map, the Receiver Sensitivity Profile (RP) of the RF coil used for signal reception, and an unknown scaling constant. If the RP is known, the MF values can be corrected and scaled, resulting in a ρ-map with a value of 1 in cerebrospinal fluid (CSF).

Novel Methods for Proton Density Quantification

Researchers have developed novel methods for rapid, simultaneous quantification of T1, T2*, and proton density. These methods include an estimation of the B1 field inhomogeneity and can achieve high-resolution images covering large volumes within clinically acceptable times of 5-10 minutes. These methods have been validated against existing techniques and have been used to quantify the whole brain using 1.5 mm^3^ voxels in less than 8 minutes.

Deep Learning Approaches for Proton Density Quantification

In addition to the novel methods mentioned above, deep learning approaches have also been developed for the quantification of absolute T1, T2, and proton density parameters from sampled MRI data. These data-driven approaches aim to provide a quantitative mapping from sampled MRI data to an intrinsic tissue parameter matrix, including proton density.

Advantages of Quantitative Proton-Density-Mapping Methods

Quantitative proton-density-mapping methods are highly valuable in qMRI because they can be compared in a single subject across different instruments at multiple time points, as well as between different subjects. This eliminates instrumental bias and allows for more accurate and reliable comparisons of tissue parameters.

Technical Details and Formulas

Proton Density Equation

The proton density (ρ) is defined as the number of MRI-visible protons per unit volume of tissue. Mathematically, it can be expressed as:

ρ = N / V

Where:
– ρ is the proton density
– N is the number of MRI-visible protons
– V is the volume of the tissue

Relaxation Time Weighting Correction

The observed signal intensity (S) in an MRI experiment is influenced by the relaxation times (T1 and T2*) of the tissue, as well as the proton density (ρ). The relationship can be expressed as:

S = ρ * (1 – e^(-TR/T1)) * e^(-TE/T2*)

Where:
– TR is the repetition time
– TE is the echo time

To obtain a pure ρ-weighted image, the relaxation time weighting must be corrected.

B0 and B1 Field Inhomogeneity Correction

Distortions in the static magnetic field (B0) and the transmitted radio-frequency (RF) field (B1) can also affect the signal intensities. These effects must be corrected to achieve accurate proton density quantification.

The B0 field inhomogeneity can be measured using a field map, and the B1 field inhomogeneity can be estimated using various techniques, such as the actual flip angle imaging (AFI) method.

Multiplication Factor (MF) Map Calculation

The corrected image intensities yield a Multiplication Factor (MF) map, which is the product of the actual ρ-map, the Receiver Sensitivity Profile (RP) of the RF coil used for signal reception, and an unknown scaling constant. Mathematically, the MF map can be expressed as:

MF = ρ * RP * Scaling Constant

If the RP is known, the MF values can be corrected and scaled, resulting in a ρ-map with a value of 1 in cerebrospinal fluid (CSF).

Practical Applications and Examples

Whole-Brain Proton Density Quantification

The novel methods for rapid, simultaneous T1, T2*, and proton density quantification have been used to quantify the whole brain using 1.5 mm^3^ voxels in less than 8 minutes. This allows for high-resolution, whole-brain proton density mapping within clinically acceptable time frames.

Tissue Water Content Estimation

Proton density (ρ) is often used to measure brain tissue water contents, assuming that fat and macromolecules do not contribute to the observed signal. This can provide valuable insights into the physiological and pathological states of the brain.

Comparison Across Instruments and Subjects

Quantitative proton-density-mapping methods are particularly useful in qMRI because they can be compared in a single subject across different instruments at multiple time points, as well as between different subjects. This eliminates instrumental bias and allows for more accurate and reliable comparisons of tissue parameters.

Numerical Examples

1. Proton Density Calculation:
2. Assume a tissue sample with a volume of 1 cm^3 and 10^23 MRI-visible protons.

3. The proton density (ρ) would be calculated as:
   ρ = N / V = 10^23 protons / 1 cm^3 = 10^23 protons/cm^3

4. Relaxation Time Weighting Correction:

5. Assume a tissue with T1 = 1000 ms and T2* = 50 ms.

6. The observed signal intensity (S) with TR = 500 ms and TE = 20 ms would be:
   S = ρ * (1 – e^(-500 ms/1000 ms)) * e^(-20 ms/50 ms) = 0.39 * ρ

7. To obtain a pure ρ-weighted image, the relaxation time weighting must be corrected by dividing the observed signal intensity by the weighting factor:
   ρ-weighted signal = S / (1 – e^(-TR/T1)) * e^(-TE/T2*) = S / 0.39 = 2.56 * ρ

8. B1 Field Inhomogeneity Correction:

9. Assume a tissue region with a B1 field inhomogeneity of 20%.
10. The observed signal intensity would be reduced by 20% due to the B1 field inhomogeneity.
11. To correct for this effect, the observed signal intensity must be divided by 0.8 (1 – 0.2) to obtain the true ρ-weighted signal.

Figures and Data Points

Figure 1: Workflow for quantitative proton density mapping, including the correction of relaxation time weighting and magnetic field distortions.

Table 1: Comparison of proton density values in different brain tissues:

Tissue	Proton Density (ρ)
Gray Matter	0.85 ± 0.02
White Matter	0.77 ± 0.03
Cerebrospinal Fluid (CSF)	1.00 ± 0.01

Conclusion

Proton density (ρ) is a crucial parameter in MRI that provides valuable information about the density of MRI-visible protons, primarily located in tissue water. Accurate measurement of proton density is essential for quantitative MRI (qMRI) as it can be compared across different instruments, subjects, and time points, eliminating instrumental bias.

This comprehensive guide has covered the underlying principles of proton density measurement, the technical details and formulas involved, and the latest advancements in the field, including novel methods for rapid, simultaneous quantification of T1, T2*, and proton density, as well as deep learning approaches for proton density quantification. The practical applications and numerical examples provided should serve as a valuable resource for physics students and researchers working in the field of MRI and qMRI.

References

1. ProQuest. (2014). Quantitative proton density mapping: correcting for relaxation time weighting and B0 inhomogeneity. Retrieved from https://www.proquest.com/docview/1507160360
2. Wiley Online Library. (2007). Novel method for rapid, simultaneous T1, T*2, and proton density quantification. Retrieved from https://onlinelibrary.wiley.com/doi/10.1002/mrm.21165
3. arXiv. (2018). Absolute T1, T2 and Proton Density Parameters from Deep Learning. Retrieved from https://arxiv.org/pdf/1806.07453
4. ResearchGate. (2016). Evaluating quantitative proton-density-mapping methods. Retrieved from https://www.researchgate.net/publication/303827703_Evaluating_quantitative_proton-density-mapping_methods_Proton-Density_Mapping
5. PMC. (2019). Evaluating quantitative proton‐density‐mapping methods. Retrieved from https://www.ncbi.nlm.nih.gov/pmc/articles/PMC6204063/