Bildnachweis – “Freundschaft an Bord”(CC DURCH-NC-ND 2.0) durch Elf-8
Diskussionspunkte
- Einführung in die Parabolreflektorantenne
- Übersicht der Parabolreflektorantenne
- Anwendungen der Parabolreflektorantenne
- Eigenschaften
- Geometrieanalyse
- Richtwirkung der Parabolreflektorantenne
- Apertureffizienz der Parabolreflektorantenne
- Mathematische Probleme
Einführung in die Parabolreflektorantenne
Antenne oder Strahler ist ein Mittel zum Strahlen und Empfangen elektromagnetischer Informationen. Parabolreflektorantenne ist eine der weit verbreiteten Antennen. Es ist ein besonderer Typ von Reflektorantennen. Der Einsatz von Reflektorantennen begann mit dem Beginn des Zweiten Weltkriegs mit der Weiterentwicklung der Kommunikationstechnologien.
The most straight-forward reflector and more comfortable to implement the reflector antenna is ‘Plane Reflector’ antenna. There are some other types of reflectors also, like – corner reflector, parabolic reflector, Cassegrain reflectors, spherical reflectors. Parabolic reflectors have another type known as ‘Front fed parabolic reflector antenna’.
Was ist eine Hornantenne? Erkunden hier!
Übersicht der Parabolreflektorantenne
Die Strahlungsparameter einer Reflektorantenne können durch Verbesserung des Strukturmusters des Bodens verbessert werden. Auf diesem Gebiet kommt für diesen Parabolreflektor die optische Wissenschaft ins Spiel. Die optische Mathematik beweist, dass einfallende parallele Strahlen durch Reflexion an einer parabelförmigen Struktur zu einem bestimmten Punkt (bekannt als Brennpunkt) konvergiert werden können.
Die reflektierten Wellenformen treten als paralleler Strahl aus. Dies ist ein mathematisches Phänomen, das als “Reziprozitätsregel” bekannt ist. Der proportionierte Punkt wird als Scheitelpunkt bezeichnet. Die ausgehenden, reflektierten Strahlen werden als kollimiert bezeichnet (da sie parallel sind). Obwohl die praktischen Beobachtungen gezeigt haben, dass die austretenden Strahlen nicht als paralleler Strahl bezeichnet werden können, unterscheiden sie sich geringfügig von der richtigen Form.
Der Sender dieser Antenne befindet sich im Allgemeinen an den Brennpunkten der Schale oder des Reflektors. Diese Art der Einrichtung wird als “Front-Feed” bezeichnet. Wir werden im nächsten Teil dieses Artikels eine Analyse dieser Art von Parabolreflektoren diskutieren.
Was macht eine Übertragungsleitung? Erforschen!
Anwendungen der Parabolreflektorantenne

Eine der größten Reflektorantennen in Deutschland für Satellitenkommunikation, Image Credit – Richard Bartz, München aka Makro-Freak, Erdfunkstelle Raisting 2, CC BY-SA 2.5
Parabolreflektoren sind eine der weit verbreiteten, hocheffizienten Antennen, deren Nachfrage von Tag zu Tag steigt. Vom Empfang des Signals für unser Fernsehgerät bis zur Übertragung des Signals für die Raumstationen findet dieser Antennentyp Anwendungen in nahezu allen Bereichen der Kommunikationstechnologie. Einige der bemerkenswerten sind – auf Flughäfen, in Satelliten, in Raumstationen, in Teleskopen usw.
Eigenschaften
Einige signifikante Eigenschaften des Parabolreflektors sind unten angegeben. Die Eigenschaften betreffen Aperturamplitude, Polarisationseigenschaften, Phasenwinkel usw.
- Der Magnitudenanteil hängt vom Abstand der Einspeisung zur Reflektoroberfläche ab. Die Proportionalität variiert von Struktur zu Struktur. Wie bei einer parabelförmigen Form ist sie umgekehrt proportional zum Quadrat des Radius der Parabel, und bei einer zylindrischen Struktur ist die Beziehung umgekehrt proportional zu ρ.
- Der Brennpunkt des Reflektors wirkt für verschiedene Arten von geometrischen Konfigurationen unterschiedlich. Die zylindrische Struktur hat eine Linienquelle und parabolische Strukturen haben eine Punktquelle.
- Wenn der Vorschub lineare Polarisationen parallel zur Zylinderachse aufweist, besteht keine Möglichkeit von Kreuzpolarisationen. Parabolische Strukturen haben nicht die gleiche Eigenschaft.
Überprüfen Sie das Strahlungsmuster von Yagi Uda Antenne!
Geometrische Analyse
Wenn eine geometrisch perfekte Parabel um ihre Achse gedreht wird, entsteht eine andere Struktur. Diese Struktur ist als Parabolreflektor bekannt. So entsteht ein parabolisch geformter Reflektor. Es gibt einen bestimmten Grund für die Form dieses Reflektors. Die parabolische Form hilft, aus den austretenden Strahlen eine einfache und ebene Wellenform zu erzeugen.
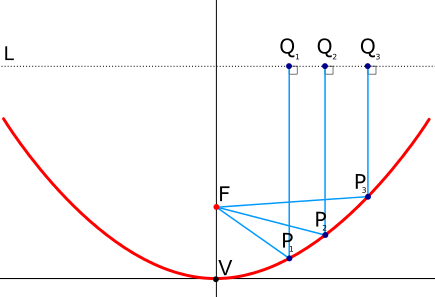
Aus dem Bild können wir ersehen, dass die geometrische Länge OP + PQ einen konstanten Wert für das Entwerfen ergibt.
Wir können schreiben, OP + PQ = 2f; 2f ist der konstante Term.
Nehmen wir das an OP = r und so kommt PQ als PQ = r * cosϴ.
Nun ist der Wert von OP + PQ nach dem Ersetzen der Werte,
OP + PQ = r + r * cosϴ = 2f
Oder r (1 + cosϴ) = 2f
Oder r = 2f / (1 + cosϴ) = f * sec2(ϴ / 2)
In der Antennentheorie müssen wir nun die Grundlagen des Koordinatensystems in Form von Sachleistungen halten. Die obige Gleichung kann in rechteckigen Koordinatensystemen unter Verwendung von x`, y`, z` geschrieben werden. Das ergibt die folgende Form.
r + r * cosϴ = √ [(x`) 2 + (y`) 2 + (z`) 2] + z` = 2f
Lassen Sie uns den Einheitsvektor herausfinden, der senkrecht zur Tangente des Reflexionspunktes ist.
f – r * cos2(ϴ / 2) = 0 = S.
Durch einige Rechenoperationen finden wir den Einheitsvektor. Es wird unten beschrieben.
n = N / | N | = – (a) `r cos (ϴ / 2) + – (a) `ϴ Sünde (ϴ / 2)
Mithilfe der geometrischen Analyse können wir nun einen Ausdruck für den Neigungswinkel finden. Es wird unten beschrieben.
tan (ϴ0) = (d / 2) Z.0
Das Z0 ist die Messung der Entfernung von der Achse zum Brennpunkt. Mathematische Ausdrücke können es auch darstellen.
Z0 = f – [(x02 + y02) / 4f]
Oder Z.0 = f – [(d / 2)2/ 4f]
Oder Z.0= f – d2 / 16f
Überprüfen wir den Wert von tan (ϴ0) nach dem Ersetzen des Wertes von Z0.
tan (ϴ0) = [(f / 2d) / {(f / d)2 – (1/16)}]
Entdecken Sie die Anwendungen der Helixantenne! Klick hier!
Richtwirkung der Parabolreflektorantenne
Bevor wir uns mit der Richtwirkung einer Parabolantenne befassen, informieren Sie uns über die Richtwirkung einer Antenne.
Die Richtwirkung einer Antenne ist definiert als das Verhältnis der Strahlungsintensität einer Antenne in einer bestimmten Richtung zur gemittelten Strahlungsintensität über alle Richtungen.
Die Richtwirkung wird als Parameter zur Berechnung der Gütezahl der Antenne betrachtet. Der folgende mathematische Ausdruck beschreibt die Richtwirkung.
D = U / U.0 = 4πU / P.rad
Wenn die Richtung nicht angegeben ist, ist die Standardrichtung die Richtung der maximalen Strahlungsintensität.
Dmax = D0 = U.max / U.0 = 4πUmax / Prad
Hier ist ‘D’ die Richtwirkung und hat keine Richtung, da es sich um ein Verhältnis handelt. U ist die Strahlungsintensität. U.max ist die maximale Strahlungsintensität. U.0 ist die Strahlungsintensität der isotropen Quelle. P.rad ist die gesamte abgestrahlte Leistung. Seine Einheit ist Watt (W).
U = ½ r2 * | E (r, ϴ = π) |2 * √ (ε / μ)
Für U (ϴ = π) und Ersetzen des Energiewerts E wird aus dem vorherigen Wert –
U (ϴ = π) = [16 π2 f2 * Pt * | ∫.0 ϴ tan (ϴ / 2) * √ (G.f (ϴ)) dϴ |2] / 4πλ2
Die Direktivität kommt als – D = U / U.0 = 4πU / P.rad
Oder D = [16 π2 f2 * | ∫.0 ϴ tan (ϴ / 2) * √ (G.f (ϴ)) dϴ |2] /2
Apertureffizienz der Parabolreflektorantenne

Mikrowellen-Relaisschalen, eine Art Reflektorantenne, Image Credit- Bidgee, Parabolantennen auf einem Telekommunikationsturm auf Willans Hill, CC BY-SA 2.5 AU
Der mathematische Ausdruck für die Parabolreflektorantenne ist unten angegeben.
εap =s * εt * εp * εx * εb * εr
Hier
εap repräsentiert die Apertureffizienz.
εs ist Spillover-Effizienz. Es kann als der Teil der Leistung definiert werden, der von der Einspeisung übertragen und von der Oberfläche der Reflexion parallel geschaltet wird.
εt repräsentiert die Effizienz der Verjüngung. Es kann als die Singularität der Streuung der Größe für das Feed-Design über die Oberfläche des Reflektors beschrieben werden.
εp gibt uns die Effizienz der Phase. Es kann als die Gleichmäßigkeit der praktischen Feldphase über die Ebene der Apertur beschrieben werden.
εx repräsentiert die Effizienz der Polarisation.
εb ist die Effizienz des Rückstands.
Und εr stellt die Fehlereffizienz dar, berechnet über die gesamte Reflektorfläche.
Mathematisches Problem
1. Eine Parabolreflektorantenne hat einen Durchmesser von 10 Metern. Das f / d-Verhältnis wird mit 0.5 angegeben. Die Betriebsfrequenz ist auf 3 GHz eingestellt. Die Antenne, die mit dem Reflektor gespeist wird, ist symmetrisch aufgebaut. Es ist auch gegeben, dass –
Gf (ϴ) = 6 cos2ϴ; wo ϴo ≤ ϴ ≤ 90o und null an jedem anderen Punkt.
Berechnen Sie nun i) die Apertureffizienz (εap). ii) Richtwirkung der Antenne. iii) Verjüngungseffizienz und Effizienz des Überlaufens. iv) Ermitteln Sie die Richtwirkung der Antenne, wenn die Aperturphasenabweichung auf π / 4 Radian eingestellt ist.
Lösung:
Wir wissen, dass der Neigungswinkel durch den folgenden Ausdruck gegeben ist.
tan (ϴ0) = [(f / 2d) / {(f / d)2 – (1/16)}]
Oder tan (ϴ0) = [(0.5 · 0.5) / {(0.5 · 0.5) – (1/16)}]
Oder tan (ϴ0) = 0.25 / 0.0625
Oder ϴ0 = 53.13o
Die Apertureffizienz ist gegeben als –
εap = 24 [(Sünde2 (26.57o) + ln {cos (26.57o)}]2 * Kinderbett2(26.57o)
oder εap = 0.75
Der Öffnungswirkungsgrad beträgt also 75%.
Lassen Sie uns nun die Richtwirkung der Antenne herausfinden.
Es kann wie folgt berechnet werden.
D = 0.75 * [π * (100)]2
Oder D = 74022.03
Oder D = 48.69 dB.
Die Überlauffrequenz beträgt εs.
εs = 2 cos3 |0 53.13 / 2 cos3 |0 90
oder εs = 0.784
Die Spillover-Effizienz der Antenne beträgt also 78.4%.
Jetzt Zeit für die Berechnung der Effizienz des Gewindeschneiders. Die Tapper-Effizienz wird als & epsi; dargestelltt.
εt = (2 · 0.75) / 1.568
oder εt = 0.9566
Der Tapper-Wirkungsgrad für die Parabolreflektorantenne beträgt also 95.66%.
Jetzt wird die Aperturphasenabweichung auf π / 4 Radian eingestellt.
Das heißt m = π / 4 = 0.7854
Wir wissen, dass D / D.0 ≥ [1 – m2/ 2]2
Oder D / D.0 ≥ [1 – (0.7854 * 0.7854) / 2]2
Oder D / D.0 ≥ 0.4782737
Oder D ≥ 0.4782737 * D.0.
Oder D = 0.4782737 * 74022.03
Oder D = 35402.8
Oder D = 45.5 dB.
Die Richtwirkung unter den gegebenen Bedingungen beträgt 45.5 dB.

Hi, I am Sudipta Roy. I have done B. Tech in Electronics. I am an electronics enthusiast and am currently devoted to the field of Electronics and Communications. I have a keen interest in exploring modern technologies such as AI & Machine Learning. My writings are devoted to providing accurate and updated data to all learners. Helping someone in gaining knowledge gives me immense pleasure.
Let’s connect through LinkedIn –