The Orbital Velocity Formula: A Comprehensive Guide for Physics Students

The orbital velocity formula is a fundamental concept in physics and astronomy that allows us to calculate the velocity at which a satellite or a celestial body must move to maintain a stable orbit around another body. This formula is a crucial tool for understanding the dynamics of celestial bodies and designing spacecraft trajectories.

Understanding the Orbital Velocity Formula

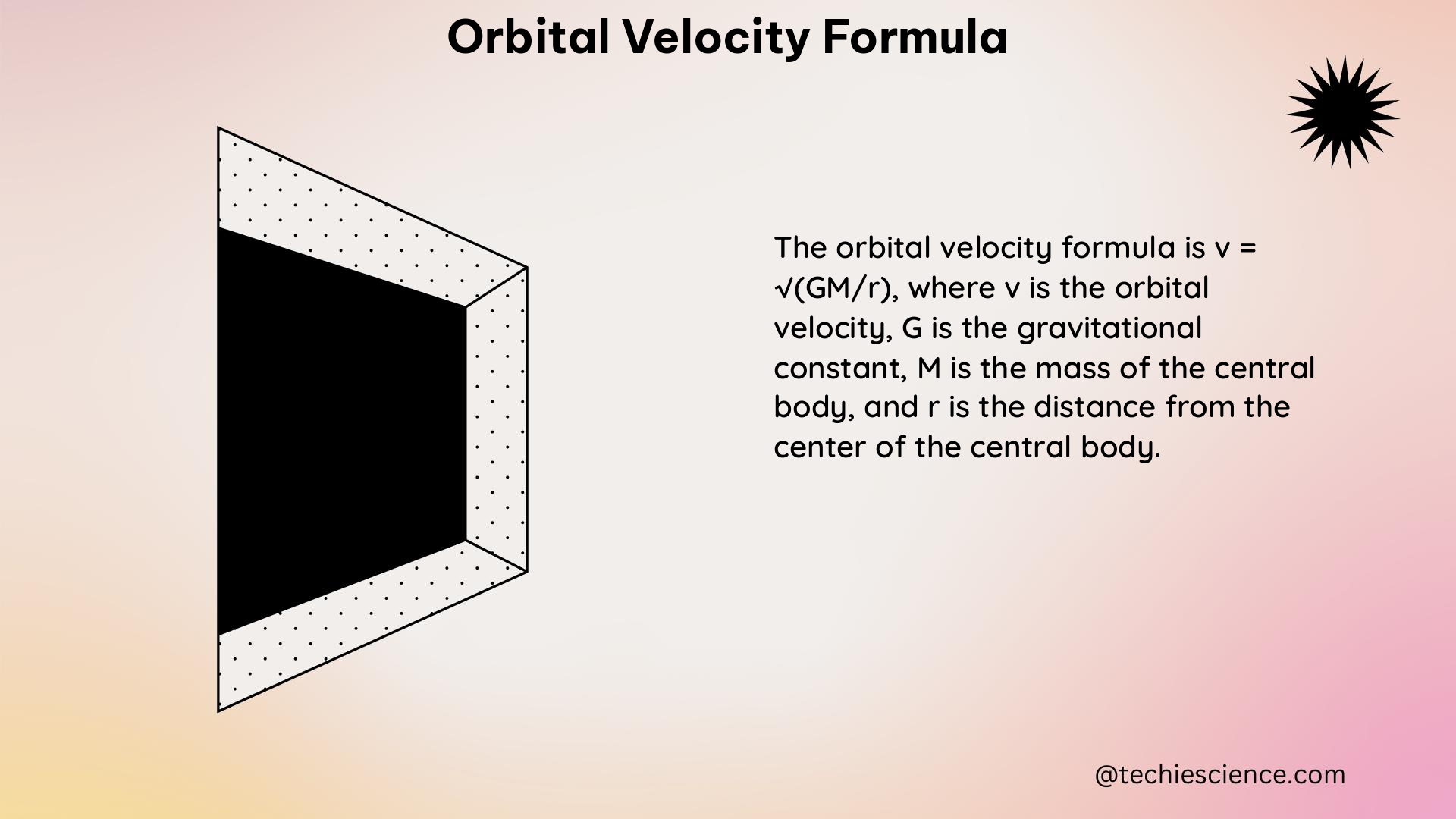
The orbital velocity formula is given by:

v = √(GM/R)

where:

• v is the orbital velocity
• G is the gravitational constant (6.67408 × 10^-11 m^3 kg^-1 s^-2)
• M is the mass of the central body (e.g., Earth, Jupiter, etc.)
• R is the radius of the orbit

This formula shows that the orbital velocity depends only on the mass of the central body and the radius of the orbit, and not on the mass of the satellite or celestial body in orbit. This is because the force of gravity, which keeps the satellite in orbit, depends only on the mass of the central body and the distance between the two bodies.

Calculating Orbital Velocity: Examples and Applications

Let’s explore some examples and applications of the orbital velocity formula.

Example 1: Calculating the Orbital Velocity of a Satellite around the Earth

To calculate the orbital velocity of a satellite around the Earth, we can use the following values:

• M = 5.9722 × 10^24 kg (mass of the Earth)
• R = 6.5 × 10^6 m (radius of the Earth’s orbit)

Substituting these values into the formula, we get:

v = √[(6.67408 × 10^-11 m^3 kg^-1 s^-2) × (5.9722 × 10^24 kg) / (6.5 × 10^6 m)]
v = 7.5 × 10^3 m/s (approximately)

This means that the satellite must move at a speed of 7.5 km/s to maintain a stable orbit around the Earth.

Example 2: Calculating the Orbital Velocity using the Period of the Orbit

Another way to calculate the orbital velocity is to use the formula:

v = 2πR/T

where T is the period of the orbit, which is the time it takes for the satellite to complete one full revolution around the central body.

For example, if we know that the period of the satellite’s orbit is 90 minutes (T = 5400 seconds), we can use the formula to calculate the orbital velocity:

v = 2π(6.5 × 10^6 m) / (5400 s)
v = 7.5 × 10^3 m/s (approximately)

This confirms the result we obtained using the first formula.

Applications of the Orbital Velocity Formula

The orbital velocity formula has numerous applications in various fields, including:

1. Satellite and Spacecraft Design: The formula is used to determine the velocity required for a satellite or spacecraft to maintain a stable orbit around a planet or other celestial body.

2. Planetary and Stellar Dynamics: The formula is used to study the motion of planets, moons, and other celestial bodies around their parent stars or other massive objects.

3. Gravitational Slingshot Maneuvers: The formula is used to calculate the velocity changes required for spacecraft to perform gravitational slingshot maneuvers, where they use the gravity of a planet or other body to gain or lose velocity.

4. Orbital Mechanics: The formula is a fundamental tool in the field of orbital mechanics, which is the study of the motion of objects in orbit around other objects.

5. Astronomy and Astrophysics: The formula is used to understand the dynamics of binary star systems, exoplanets, and other celestial phenomena involving orbiting bodies.

Factors Affecting Orbital Velocity

The orbital velocity formula shows that the velocity of a satellite or celestial body in orbit depends on two key factors:

1. Mass of the Central Body: The greater the mass of the central body, the higher the orbital velocity required to maintain a stable orbit. This is because the gravitational force exerted by the central body is proportional to its mass.

2. Radius of the Orbit: The orbital velocity is inversely proportional to the square root of the radius of the orbit. As the radius of the orbit increases, the orbital velocity decreases.

It’s important to note that the orbital velocity formula assumes a circular orbit. For elliptical orbits, the formula needs to be modified to account for the varying distance between the satellite and the central body.

Limitations and Assumptions of the Orbital Velocity Formula

The orbital velocity formula is based on several assumptions and simplifications:

1. Circular Orbit: The formula assumes that the orbit is circular, with a constant radius. In reality, most orbits are elliptical, with varying distances from the central body.

2. Uniform Gravitational Field: The formula assumes a uniform gravitational field, where the gravitational acceleration is constant throughout the orbit. In reality, the gravitational field can vary due to factors such as the shape of the central body and the presence of other celestial bodies.

3. Negligible Atmospheric Drag: The formula does not consider the effects of atmospheric drag, which can significantly impact the orbital velocity of satellites in low-Earth orbits.

4. Constant Mass: The formula assumes that the mass of the central body remains constant throughout the orbit. In reality, the mass of a celestial body can change due to factors such as mass loss or accretion.

It’s important to keep these limitations and assumptions in mind when using the orbital velocity formula, especially for more complex or realistic scenarios.

Conclusion

The orbital velocity formula is a fundamental concept in physics and astronomy that allows us to calculate the velocity at which a satellite or a celestial body must move to maintain a stable orbit around another body. This formula is a crucial tool for understanding the dynamics of celestial bodies and designing spacecraft trajectories.

By understanding the factors that affect orbital velocity, such as the mass of the central body and the radius of the orbit, we can gain valuable insights into the behavior of orbiting objects and apply this knowledge to a wide range of applications, from satellite design to the study of planetary and stellar dynamics.

As with any scientific formula, it’s important to be aware of the limitations and assumptions underlying the orbital velocity formula, and to use it judiciously in the appropriate contexts. By mastering this concept, physics students can develop a deeper understanding of the fundamental principles of orbital mechanics and their practical applications.

References

1. Orbital Velocity Formula – Solved Example with Equations – BYJU’S. https://byjus.com/orbital-velocity-formula/
2. Circular Velocity and Escape Velocity – Lesson – Study.com. https://study.com/academy/lesson/circular-velocity-escape-velocity.html
3. Orbital Velocity – an overview | ScienceDirect Topics. https://www.sciencedirect.com/topics/physics-and-astronomy/orbital-velocity