Mastering Orbital Velocity: A Comprehensive Guide for Physics Students

by

Orbital velocity is a fundamental concept in orbital mechanics, describing the speed at which an object orbits around a central body, such as a planet or a star. This velocity is crucial in understanding the dynamics of celestial bodies and the design of spacecraft and satellites. In this comprehensive guide, we will delve into the intricacies of orbital velocity, exploring the underlying physics, formulas, and practical applications.

Understanding the Basics of Orbital Velocity

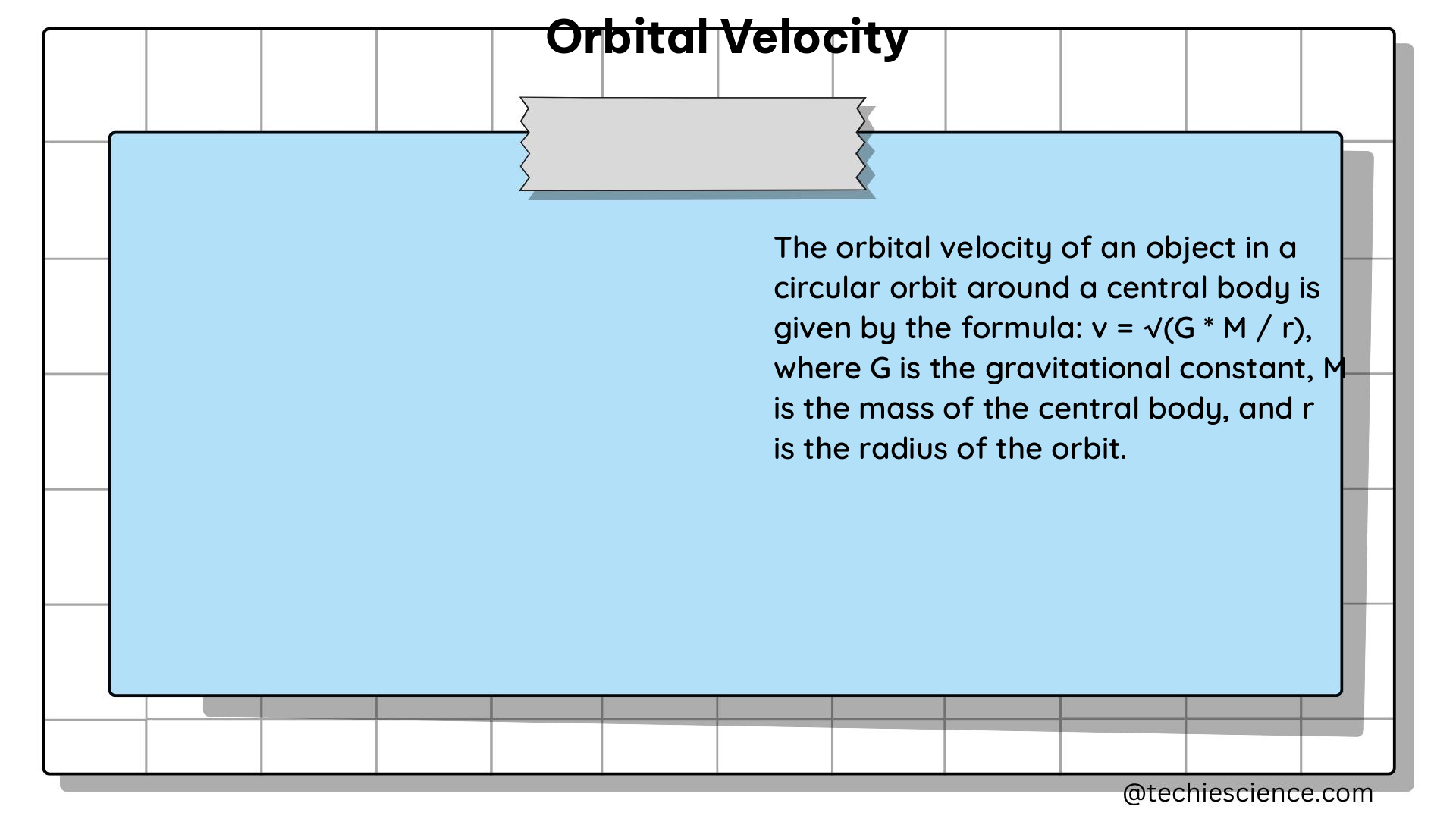
Orbital velocity, denoted as v, is the speed at which an object orbits around a central body. This velocity is determined by the balance between the gravitational force exerted by the central body and the centrifugal force acting on the orbiting object. The formula for orbital velocity is given by:

v = √(G * M / R)

Where:
– G is the gravitational constant, approximately 6.67 × 10^-11 N⋅m^2/kg^2
– M is the mass of the central body
– R is the orbital radius, which is the distance between the center of the central body and the orbiting object

This formula is derived from the principles of Newtonian mechanics and is a fundamental relationship in orbital mechanics.

Factors Affecting Orbital Velocity

orbital velocity

The orbital velocity of an object is influenced by several key factors:

  1. Mass of the Central Body: The mass of the central body, M, has a direct impact on the orbital velocity. A more massive central body will result in a higher orbital velocity, as the gravitational force exerted on the orbiting object is greater.

  2. Orbital Radius: The orbital radius, R, is the distance between the center of the central body and the orbiting object. As the orbital radius increases, the orbital velocity decreases, following the inverse square root relationship in the formula.

  3. Orbital Period: The orbital period, T, is the time it takes for an object to complete one full revolution around the central body. The orbital period and orbital velocity are inversely related, as a shorter orbital period corresponds to a higher orbital velocity.

  4. Kepler’s Third Law: The relationship between the orbital period and the orbital radius is described by Kepler’s third law, which states that the square of the orbital period is proportional to the cube of the orbital radius. This law can be expressed mathematically as:

T^2 = (4π^2 / G * M) * R^3

This equation allows for the calculation of the orbital period given the orbital radius and the mass of the central body.

Examples of Orbital Velocity

Let’s consider some practical examples of orbital velocity:

  1. Low Earth Orbit (LEO): A satellite in a low Earth orbit, at an altitude of 220 km above the Earth’s surface, has an orbital velocity of approximately 7,750 m/s (27,900 km/h or 17,500 mph).

  2. Earth’s Orbit around the Sun: The Earth, in its orbit around the Sun, has an orbital velocity of approximately 29,800 m/s (107,000 km/h or 66,600 mph).

  3. Geostationary Orbit: A geostationary satellite, orbiting the Earth at an altitude of 35,786 km, has an orbital velocity of approximately 3,070 m/s (11,000 km/h or 6,900 mph).

  4. Orbital Velocity of the Moon: The Moon, in its orbit around the Earth, has an orbital velocity of approximately 1,020 m/s (3,700 km/h or 2,300 mph).

  5. Orbital Velocity of the International Space Station (ISS): The ISS, orbiting the Earth at an average altitude of 400 km, has an orbital velocity of approximately 7,660 m/s (27,600 km/h or 17,100 mph).

These examples illustrate the wide range of orbital velocities encountered in various celestial and artificial satellite systems.

Orbital Velocity Calculations

To calculate the orbital velocity of an object, you can use the formula:

v = √(G * M / R)

Where:
– v is the orbital velocity (in m/s)
– G is the gravitational constant (6.67 × 10^-11 N⋅m^2/kg^2)
– M is the mass of the central body (in kg)
– R is the orbital radius (in m)

Here’s an example calculation:

Example: Calculate the orbital velocity of a satellite orbiting the Earth at an altitude of 500 km.

Given:
– Radius of the Earth: 6,371 km
– Altitude of the satellite: 500 km
– Mass of the Earth: 5.97 × 10^24 kg

Step 1: Calculate the orbital radius.
Orbital radius = Radius of the Earth + Altitude of the satellite
Orbital radius = 6,371 km + 500 km = 6,871 km = 6.871 × 10^6 m

Step 2: Calculate the orbital velocity.
Orbital velocity, v = √(G * M / R)
v = √(6.67 × 10^-11 N⋅m^2/kg^2 * 5.97 × 10^24 kg / 6.871 × 10^6 m)
v = 7,611 m/s

Therefore, the orbital velocity of the satellite orbiting the Earth at an altitude of 500 km is approximately 7,611 m/s.

Orbital Velocity Numerical Problems

  1. Problem: A satellite is orbiting the Earth at an altitude of 300 km. Calculate the orbital velocity of the satellite.

Given:
– Radius of the Earth: 6,371 km
– Altitude of the satellite: 300 km
– Mass of the Earth: 5.97 × 10^24 kg

Solution:
Orbital radius = Radius of the Earth + Altitude of the satellite
Orbital radius = 6,371 km + 300 km = 6,671 km = 6.671 × 10^6 m

Orbital velocity, v = √(G * M / R)
v = √(6.67 × 10^-11 N⋅m^2/kg^2 * 5.97 × 10^24 kg / 6.671 × 10^6 m)
v = 7,760 m/s

  1. Problem: The International Space Station (ISS) orbits the Earth at an average altitude of 400 km. Calculate the orbital velocity of the ISS.

Given:
– Radius of the Earth: 6,371 km
– Altitude of the ISS: 400 km
– Mass of the Earth: 5.97 × 10^24 kg

Solution:
Orbital radius = Radius of the Earth + Altitude of the ISS
Orbital radius = 6,371 km + 400 km = 6,771 km = 6.771 × 10^6 m

Orbital velocity, v = √(G * M / R)
v = √(6.67 × 10^-11 N⋅m^2/kg^2 * 5.97 × 10^24 kg / 6.771 × 10^6 m)
v = 7,660 m/s

  1. Problem: A weather satellite is orbiting the Earth in a circular orbit at an altitude of 833 km. Calculate the orbital velocity of the weather satellite.

Given:
– Radius of the Earth: 6,371 km
– Altitude of the weather satellite: 833 km
– Mass of the Earth: 5.97 × 10^24 kg

Solution:
Orbital radius = Radius of the Earth + Altitude of the weather satellite
Orbital radius = 6,371 km + 833 km = 7,204 km = 7.204 × 10^6 m

Orbital velocity, v = √(G * M / R)
v = √(6.67 × 10^-11 N⋅m^2/kg^2 * 5.97 × 10^24 kg / 7.204 × 10^6 m)
v = 7,670 m/s

These examples demonstrate the application of the orbital velocity formula to calculate the velocities of satellites and spacecraft orbiting the Earth at different altitudes.

Orbital Velocity and Kepler’s Laws

The concept of orbital velocity is closely related to Kepler’s laws of planetary motion, which describe the motion of objects orbiting a central body. Specifically, Kepler’s third law, also known as the law of harmonies, relates the orbital period and the orbital radius of an object.

Kepler’s third law states that the square of the orbital period of a planet is proportional to the cube of the semi-major axis of its orbit. Mathematically, this can be expressed as:

T^2 = (4π^2 / G * M) * R^3

Where:
– T is the orbital period (in seconds)
– R is the semi-major axis of the orbit (in meters)
– G is the gravitational constant (6.67 × 10^-11 N⋅m^2/kg^2)
– M is the mass of the central body (in kg)

This relationship allows us to calculate the orbital period given the orbital radius and the mass of the central body, or vice versa.

Orbital Velocity and Escape Velocity

Orbital velocity is also related to the concept of escape velocity, which is the minimum velocity an object needs to escape the gravitational pull of a central body. The escape velocity, denoted as v_e, is given by the formula:

v_e = √(2 * G * M / R)

Where:
– v_e is the escape velocity (in m/s)
– G is the gravitational constant (6.67 × 10^-11 N⋅m^2/kg^2)
– M is the mass of the central body (in kg)
– R is the radius of the central body (in m)

The escape velocity is always greater than the orbital velocity, as the object needs to overcome the gravitational pull of the central body to escape its influence.

Orbital Velocity and Spacecraft Design

Orbital velocity is a crucial factor in the design and operation of spacecraft and satellites. Engineers must consider the orbital velocity when determining the propulsion requirements, fuel consumption, and trajectory planning for a spacecraft. Accurate calculations of orbital velocity are essential for ensuring the successful launch, insertion, and maintenance of a spacecraft in its desired orbit.

Furthermore, orbital velocity plays a role in the design of spacecraft components, such as the thermal protection system, which must withstand the heat generated by the high-speed motion of the spacecraft through the atmosphere during launch and re-entry.

Conclusion

Orbital velocity is a fundamental concept in orbital mechanics that describes the speed at which an object orbits around a central body. This velocity is determined by the balance between the gravitational force and the centrifugal force acting on the orbiting object, and it is influenced by factors such as the mass of the central body, the orbital radius, and the orbital period.

Understanding the principles of orbital velocity is crucial for the design and operation of spacecraft, satellites, and other celestial bodies. By mastering the formulas, calculations, and practical applications of orbital velocity, physics students can gain a deeper understanding of the dynamics of the universe and the engineering challenges involved in space exploration.

Reference: