Nusselt Number | Its Important Relations and Formulas

Content: Nusselt Number

What is Nusselt number | Nusselt number definition

“The Nusselt number is the ratio of convective to conductive heat transfer across a boundary.”

https://en.wikipedia.org/wiki/Nusselt_number

• The convection and conduction heat flows in-parallel to each other.
• The surface will be normal of the boundary surface, and vertical to the mean fluid-flow.

Nusselt number equation | Nusselt number formula

Average Nusselt Number can be formulated as:

Nu = Convective heat transfer / conductive heat transfer

Nu = h/(k/L_c)

Nu = hL_c/k

where h = convective heat transfer coefficient of the flow

 L = the characteristic length

 k = the thermal conductivity of the fluid.

The Local Nusselt Number is represented as

Nu = hx/k

x = distance from the boundary surface

Significance of Nusselt number.

Thisrelates in-between convective and conductive heat transfer for the similartypes of fluids.

It also helps in enhancing the convective heat transfer through a fluid layer relative to conductive heat transfer for the same fluid.

It is useful in determining the heat transfer coefficient of the fluid.

It helps to identify the factors which are providing the resistance to the heat transfer and helps in enhancing the factors which can improve the heat transfer process.

Nusselt number correlations.

In case of free-convection, the Nusselt number is represented as the function of Rayleigh number (Ra) and Prandtl Number (Pr), In simple representation

Nu = f (Ra, Pr).

In case of forced-convection, the Nusselt number is represented as the function of Reynold’s number (Re) and Prandtl Number (Pr), in simple way

Nu = f (Re, Pr)

Nusselt number for free convection.

For Free convection at vertical wall

For Ra_L<10⁸

For horizontal Plate

1. If top surface of hot body is in cold environment

Nu_L = 0.54Ra_L^1/4     for Rayleigh number in the range 10⁴<Ra_L< 10⁷

Nu_L = 0.15Ra_L^1/3for Rayleigh number in the range 10⁷<Ra_L< 10¹¹

1. If bottom surface of hot body is in contact with cold environment
2. Nu_L = 0.52Ra_L^1/5for Rayleigh number in the range 10⁵<Ra_L< 10¹⁰

Nusselt number correlations for forced convection.

For fully developed Laminar flow over flat plate

Re < 5×10⁵, Local Nusselt number

Nu_L = 0.332 (Re_x)^1/2(Pr)^1/3

But For fully developed Laminar flow

Average Nusselt number = 2 * Local Nusselt number

Nu = 2*0.332 (Re_x)^1/2(Pr)^1/3

Nu = 0.664 (Re_x)^1/2(Pr)^1/3

For Combined laminar and Turbulent boundary layer

Nu = [0.037Re_L^4/5 – 871] Pr^1/3

Nusselt number for laminar flow | Average Nusselt number flat plate

For fully developed Laminar flow over flat plate[Forced Convection]

Re < 5×10⁵, Local Nusselt number

Nu_L = 0.332 (Re_x)^1/2(Pr)^1/3

But For fully developed Laminar flow

Average Nusselt number = 2 * Local Nusselt number

Nu = 2*0.332 (Re_x)^1/2(Pr)^1/3

Nu = 0.664 (Re_x)^1/2(Pr)^1/3

For horizontal Plate [ Free Convection]

1. If top surface of hot body is in cold environment

Nu_L = 0.54Ra_L^1/4     for Rayleigh number in the range 10⁴<Ra_L< 10⁷

Nu_L = 0.15Ra_L^1/3     for Rayleigh number in the range 10⁷<Ra_L< 10¹¹

1. If bottom surface of hot body is in contact with cold environment
2. Nu_L = 0.52Ra_L^1/5for Rayleigh number in the range 10⁵<Ra_L< 10¹⁰

Nusselt number for laminar flow in pipe

For a circular pipe with diameter D with a fully developed region throughout the pipe, Re < 2300

Nu = hD/k

Where h = convective heat transfer coefficient of the flow

 D =Diameter of pipe

 k = the thermal conductivity of the fluid.

For a circular pipe with diameter D with a Transient flow throughout the pipe, 2300 < Re < 4000

Nusselt number for turbulent flow in pipe

Nusselt Number For a circular pipe with diameter D with a turbulent flow throughout the pipe Re > 4000

According to The Dittus-Boelter equation

Nu = 0.023 Re^0.8 Prⁿ

n = 0.3 for heating, n = 0.4 for cooling

Nusselt number in terms of Reynolds number

For fully developed Laminar flow over flat plate

Re < 5×10⁵, Local Nusselt number

Nu_L = 0.332 (Re_x)^1/2(Pr)^1/3

But For fully developed Laminar flow

Average Nusselt number = 2 * Local Nusselt number

Nu = 2*0.332 (Re_x)^1/2(Pr)^1/3

Nu = 0.664 (Re_x)^1/2(Pr)^1/3

For Combined laminar and Turbulent boundary layer

Nu = [0.037Re_L^4/5 – 871] Pr^1/3

Nusselt Number For a circular pipe with diameter D with a turbulent flow throughout the pipe Re > 4000

According to The Dittus-Boelter equation

Nu = 0.023 Re^0.8 Prⁿ

n = 0.3 for heating, n = 0.4 for cooling

Local Nusselt number

For fully developed Laminar flow over flat plate[Forced Convection]

Re < 5×10⁵, Local Nusselt number

Nu_L = 0.332 (Re_x)^1/2(Pr)^1/3

But For fully developed Laminar flow

Average Nusselt number = 2 * Local Nusselt number

Nu = 2*0.332 (Re_x)^1/2(Pr)^1/3

Nu = 0.664 (Re_x)^1/2(Pr)^1/3

Nusselt number correlations for natural convection

For Laminar flow over vertical plate (natural convection)Nux = 0.59 (Gr.Pr)0.25

Where Gr = Grashoff Number

Pr = Prandtl Number

g = acceleration due to gravity

β = fluid coefficient of thermal expansion

ΔT = Temperature difference

L = characteristic length

ν = kinematic viscosity

μ = dynamic viscosity

C_p = Specific heat at constant pressure

k = the thermal conductivity of the fluid.

For Turbulent Flow

Nu = 0.36 (Gr.Pr)^1/3

Nusselt number heat transfer coefficient

Average Nusselt Number can be formulated as:

Nu = Convective heat transfer / conductive heat transfer

Nu = h/(k/L_c)

Nu = hL_c/k

where h = convective heat transfer coefficient of the flow

 L = the characteristic length

 k = the thermal conductivity of the fluid.

Local Nusselt Number is given by

Nu = hx/k

x = distance from the boundary surface

For a circular pipe with diameter D,

Nu = hD/k

Where h = convective heat transfer coefficient of the flow

 D =Diameter of pipe

 k = the thermal conductivity of the fluid.

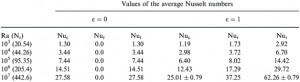
Nusselt number table | Nusselt number of air.

Biot number vs. Nusselt number

Both are dimensionless number used to find the convective heat transfer coefficient between wall or solid body and the fluid flowing over the body. They both are formulated as hL_c/k. However, Biot Number is used for solids and Nusselt number is used for fluids.

In Biot number formula hL_c/k for the thermal conductivity (k) of solid is taken into consideration, while in Nusselt Number the thermal conductivity (k) of fluid flowing over the solid is taken into consideration.

Biot number is useful in identifying whether the small body has homogenous temperature all around or not.

Nusselt number heat exchanger

For a circular pipe with diameter D with a fully developed region throughout the pipe, Re < 2300

Nu = hD/k

Where h = convective heat transfer coefficient of the flow

 D =Diameter of pipe

 k = the thermal conductivity of the fluid.

For a circular pipe with diameter D with a Transient flow throughout the pipe, 2300 < Re < 4000

Nusselt number for turbulent flow in pipe: Nusselt Number For a circular pipe with diameter D with a turbulent flow throughout the pipe Re > 4000

According to The Dittus-Boelter equation

Nu = 0.023 Re^0.8 Prⁿ

n = 0.3 for heating, n = 0.4 for cooling

Problems

Q.1)The non-dimensional fluid temp at vicinity of surface of a convectively-cool flat plate is specified as given below . Here y is computed vertical to the plate, L is the plate’s length, and a, b and c are constant. T_w and T_∞ are wall and ambient temp, correspondingly.

If the thermal conductivity (k)and the wall heat flux(q′′) then proof that, Nusselt number

Nu = q/Tw – T / (L/k) = b

Solution:

Tw – T (Tw – T) = a + b (y/L) + c (y/L) = 0

at y = 0

Nu = q (tw – T )(L/k) = b

Hence proved

Q.2) Water flowing through a tube having dia. of 25 mm at velocity of 1 m/sec. Thegiven properties of water are density ρ = 1000kg/m³, μ = 7.25*10^-4 N.s/m², k= 0.625 W/m. K, Pr = 4.85. and Nu = 0.023Re^0.8 Pr^0.4. Then calculate what will be convective heat transfer’s coefficient?

GATE ME-14-SET-4

Solution:

Re = p VD = 1000 x 1 x 25 x 10

(-3) (7.25)

Re = 34482.75

Pr = 4.85, Nu = 0.023Re^0.8 Pr^0.4,

Nu = 0.023*34482.758^0.8 * 4.85^0.4

Nu = 184.5466 = hD/k

h = 184.5466 / 0.625 (25 x 10 (-3)

FAQ

1. What is the difference between Biot number and Nusselt number?

Ans: Both are dimensionless number used to find the convective heat transfer coefficient between wall or solid body and the fluid flowing over the body. They both are formulated as hL_c/k. However, Biot Number is used for solids and Nusselt number is used for fluids.

In Biot number formula hL_c/k for the thermal conductivity (k) of solid is taken into consideration, while in Nusselt Number, the thermal conductivity (k) of fluid flowing over the solid is taken into consideration.

Biot number is useful in identifying whether the small body has homogenous temperature all around or not.

2. How do you find the average of a Nusselt number?

Ans: Average Nusselt Number can be formulated as:

Nu = Convective heat transfer / conductive heat transfer

Nu = h/(k/L_c)

Nu = hL_c/k

where h = convective heat transfer coefficient of the flow

 L = the characteristic length

 k = the thermal conductivity of the fluid.

Local Nusselt Number is given by

Nu = hx/k

x = distance from the boundary surface

3. how to calculate Nusselt number?

Ans: Average Nusselt Number can be formulated as:

Nu = Convective heat transfer / conductive heat transfer

Nu = h/(k/L_c)

Nu = hL_c/k

where h = convective heat transfer coefficient of the flow

 L = the characteristic length

 k = the thermal conductivity of the fluid.

Local Nusselt Number is given by

Nu = hx/k

x = distance from the boundary surface

For fully developed Laminar flow over flat plate[Forced Convection]

Re < 5×10⁵, Local Nusselt number

Nu_L = 0.332 (Re_x)^1/2(Pr)^1/3

But For fully developed Laminar flow

Average Nusselt number = 2 * Local Nusselt number

Nu = 2*0.332 (Re_x)^1/2(Pr)^1/3

Nu = 0.664 (Re_x)^1/2(Pr)^1/3

4. Can Nusselt number be negative?

Ans: Average Nusselt Number can be formulated as:

Nu = Convective heat transfer / conductive heat transfer

Nu = h/(k/L_c)

Nu = hL_c/k

where h = convective heat transfer coefficient of the flow

 L = the characteristic length

 k = the thermal conductivity of the fluid.

For all the properties being constant, heat transfer coefficient is directly proportional to Nu.

Thus, if heat transfer coefficient is negative then the Nusselt number can also be negative.

5. Nusselt number vs. Reynolds number

Ans: In forced convection, the Nusselt number is the function of Reynolds number and Prandtl Number

Nu = f (Re, Pr)

For a circular pipe with diameter D with a fully developed region throughout the pipe, Re < 2300

Nu = hD/k

Where h = convective heat transfer coefficient of the flow

 D =Diameter of pipe

 k = the thermal conductivity of the fluid.

For a circular pipe with diameter D with a Transient flow throughout the pipe, 2300 < Re < 4000

Nusselt number for turbulent flow in pipe

Nusselt Number For a circular pipe with diameter D with a turbulent flow throughout the pipe Re > 4000

According to The Dittus-Boelter equation

Nu = 0.023 Re^0.8 Prⁿ

n = 0.3 for heating, n = 0.4 for cooling

Nusselt number in terms of Reynolds number

For fully developed Laminar flow over flat plate

Re < 5×10⁵, Local Nusselt number

Nu_L = 0.332 (Re_x)^1/2(Pr)^1/3

But For fully developed Laminar flow

Average Nusselt number = 2 * Local Nusselt number

Nu = 2*0.332 (Re_x)^1/2(Pr)^1/3

Nu = 0.664 (Re_x)^1/2(Pr)^1/3

For Combined laminar and Turbulent boundary layer

Nu = [0.037Re_L^4/5 – 871] Pr^1/3

Nusselt Number For a circular pipe with diameter D with a turbulent flow throughout the pipe Re > 4000

According to The Dittus-Boelter equation

Nu = 0.023 Re^0.8 Prⁿ

n = 0.3 for heating, n = 0.4 for cooling

6. Calculate Nusselt number with Reynolds?

Ans: For fully developed Laminar flow over flat plate[Forced Convection]

Re < 5×10⁵, Local Nusselt number

Nu_L = 0.332 (Re_x)^1/2(Pr)^1/3

But For fully developed Laminar flow

Average Nusselt number = 2 * Local Nusselt number

Nu = 2*0.332 (Re_x)^1/2(Pr)^1/3

Nu = 0.664 (Re_x)^1/2(Pr)^1/3

For Combined laminar and Turbulent boundary layer

Nu = [0.037Re_L^4/5 – 871] Pr^1/3

7. What is physical significance of Nusselt number?

Ans: It gives the relation between convective heat transfer and conductive heat transfer for the same fluid.

It also helps in enhancing the convective heat transfer through a fluid layer relative to conductive heat transfer for the same fluid.

It is useful in determining the heat transfer coefficient of the fluid.

It helps to identify the factors which are providing the resistance to the heat transfer and helps in enhancing the factors which can improve the heat transfer process.

8. Why is a Nusselt number always greater than 1?

Ans: This is ratio,In the meantime actual heat transfer cannot become less than 1. Nusselt number is always greater than 1.

9. What is the difference between the Nusselt number and the Peclet number What is their physical significance?

Ans: The Nusselt number is the ratio of convective or actual heat-transfer to conductive heat transfer around a borderline, if convective heat transfer become prominent in the system than conductive heat transfer, Nusselt number will be high.

Whereas, product of Reynold’s number and Prandtl number is represented as Peclet Number. Asit become higher, this will signify high flow rates and flow momentum transfer generally.

10. What is an average Nusselt number How does it differ from a Nusselt number?

Ans: For fully developed Laminar flow over flat plate

Re < 5×10⁵, Local Nusselt number

Nu_L = 0.332 (Re_x)^1/2(Pr)^1/3

But For fully developed Laminar flow

Average Nusselt number = 2 * Local Nusselt number

Nu = 2*0.332 (Re_x)^1/2(Pr)^1/3

Nu = 0.664 (Re_x)^1/2(Pr)^1/3

11. What is the Nusselt number formula for free convection from fuel inside a closed cylinder tank?

Ans: Average Nusselt Number can be formulated as:

Nu = Convective heat transfer / conductive heat transfer

Nu = h/(k/L_c)

Nu = hL_c/k

where h = convective heat transfer coefficient of the flow

 L_c = the characteristic length

 k = the thermal conductivity of the fluid.

For horizontal cylindrical tank L_c = D

Thus, Nu = hD/k

12. Nusselt number for cylinder

Ans: Average Nusselt Number can be formulated as:

Nu = Convective heat transfer / conductive heat transfer

Nu = h/(k/L_c)

Nu = hL_c/k

where h = convective heat transfer coefficient of the flow

 L_c = the characteristic length

 k = the thermal conductivity of the fluid.

For horizontal cylindrical tank L_c = D

Thus, Nu = hD/k

For vertical Cylinder L_c = Length / height of the cylinder

Thus, Nu = hL/k

13. Nusselt number for flat plate

Ans: For horizontal Plate

1. If top surface of hot body is in cold environment

Nu_L = 0.54Ra_L^1/4     for Rayleigh number in the range 10⁴<Ra_L< 10⁷

Nu_L = 0.15Ra_L^1/3     for Rayleigh number in the range 10⁷<Ra_L< 10¹¹

1. If bottom surface of hot body is in contact with cold environment

Nu_L = 0.52Ra_L^1/5     for Rayleigh number in the range 10⁵<Ra_L< 10¹⁰

For fully developed Laminar flow over flat plate

Re < 5×10⁵, Local Nusselt number

Nu_L = 0.332 (Re_x)^1/2(Pr)^1/3

But For fully developed Laminar flow

Average Nusselt number = 2 * Local Nusselt number

Nu = 2*0.332 (Re_x)^1/2(Pr)^1/3

Nu = 0.664 (Re_x)^1/2(Pr)^1/3

For Combined laminar and Turbulent boundary layer

Nu = [0.037Re_L^4/5 – 871] Pr^1/3

14. Nusselt number for laminar flow

Ans:For fully developed Laminar flow over flat plate

Re < 5×10⁵, Local Nusselt number

Nu_L = 0.332 (Re_x)^1/2(Pr)^1/3

But For fully developed Laminar flow

Average Nusselt number = 2 * Local Nusselt number

Nu = 2*0.332 (Re_x)^1/2(Pr)^1/3

Nu = 0.664 (Re_x)^1/2(Pr)^1/3

For a circular pipe with diameter D with a fully developed region throughout the pipe, Re < 2300

Nu = hD/k

Where h = convective heat transfer coefficient of the flow

 D =Diameter of pipe

 k = the thermal conductivity of the fluid.

For a circular pipe with diameter D with a Transient flow throughout the pipe, 2300 < Re < 4000

To know about Polytropic Process (click here)and Prandtl Number (Click here)