Moment of Inertia of a Hollow Sphere: A Comprehensive Guide

The moment of inertia of a hollow sphere is a crucial concept in classical mechanics, as it describes the object’s resistance to rotational motion. This comprehensive guide will delve into the theoretical foundations, derivation, and practical applications of the moment of inertia formula for a hollow sphere.

Understanding the Moment of Inertia of a Hollow Sphere

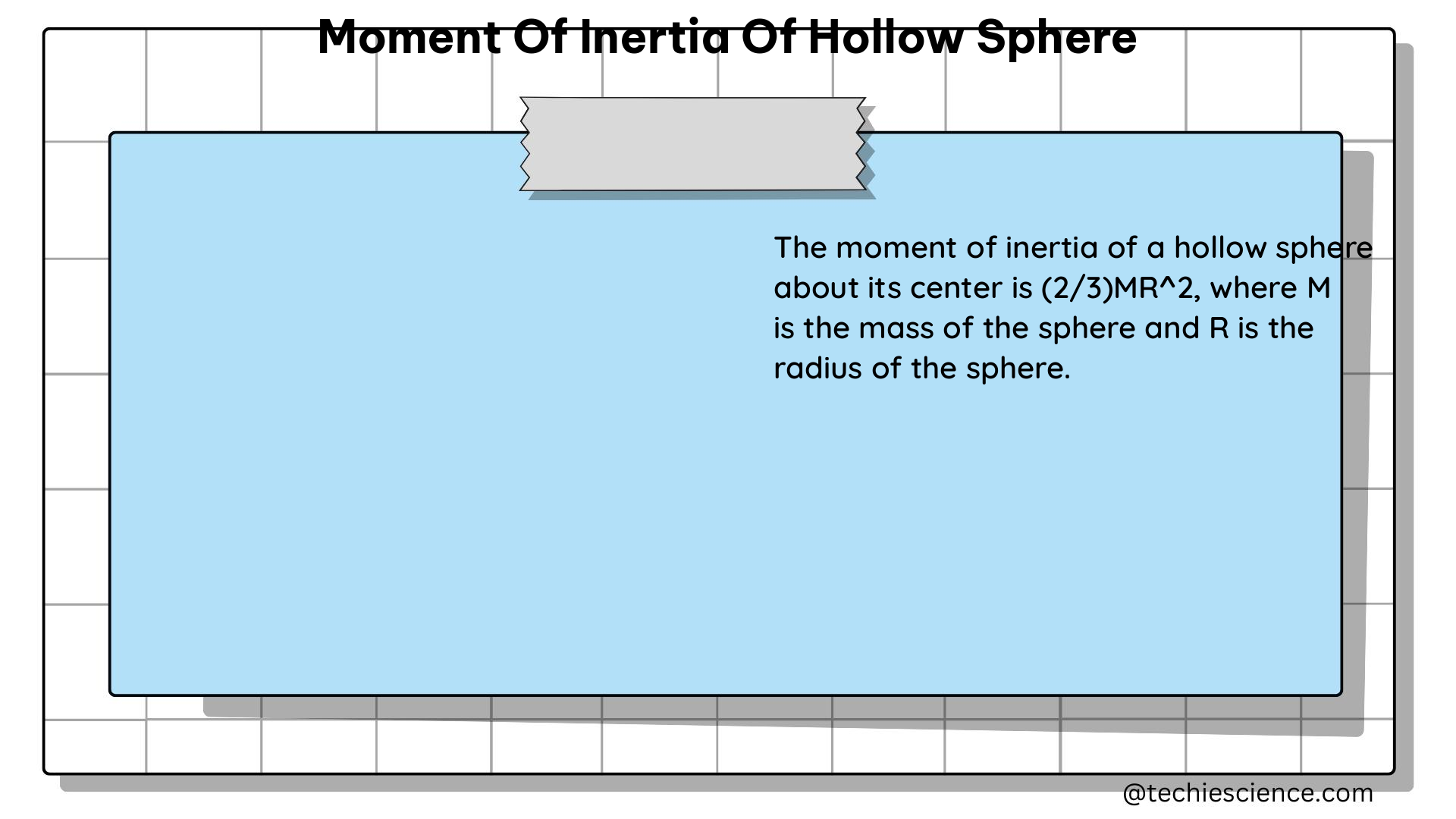
The moment of inertia of a hollow sphere is given by the formula:

$I = \frac{2}{3}MR^2$

Where:
– $I$ is the moment of inertia of the hollow sphere
– $M$ is the mass of the hollow sphere
– $R$ is the radius of the hollow sphere

This formula is derived by considering the hollow sphere as a collection of infinitesimal mass elements and summing their individual moments of inertia about the axis of rotation.

Derivation of the Moment of Inertia Formula

To derive the moment of inertia formula for a hollow sphere, we can follow these steps:

1. Divide the Sphere into Infinitesimal Mass Elements: Imagine the hollow sphere is composed of a large number of infinitesimal mass elements, each with a mass $dm$ and located at a distance $r$ from the axis of rotation.

2. Calculate the Moment of Inertia for Each Mass Element: The moment of inertia of each infinitesimal mass element is given by the formula $dI = r^2 dm$.

3. Integrate the Moment of Inertia over the Entire Sphere: To find the total moment of inertia of the hollow sphere, we need to integrate the moment of inertia of all the infinitesimal mass elements over the volume of the sphere. This can be done using spherical coordinates:

$I = \int dI = \int r^2 dm = \int_0^R \int_0^{\pi} \int_0^{2\pi} r^4 \rho \sin\theta dr d\theta d\phi$

Where $\rho$ is the density of the hollow sphere.

1. Evaluate the Integral: Evaluating the integral and simplifying the expression, we arrive at the final formula for the moment of inertia of a hollow sphere:

$I = \frac{2}{3}MR^2$

Examples and Numerical Problems

Let’s consider a few examples to illustrate the application of the moment of inertia formula for a hollow sphere.

Example 1: A hollow sphere has a mass of 55.0 kg and a radius of 0.120 m. Calculate its moment of inertia.

Given:
– $M = 55.0 \text{ kg}$
– $R = 0.120 \text{ m}$

Substituting the values into the formula:
$I = \frac{2}{3}MR^2$
$I = \frac{2}{3}(55.0 \text{ kg})(0.120 \text{ m})^2$
$I = 0.528 \text{ kg}\cdot\text{m}^2$

Therefore, the moment of inertia of the hollow sphere is 0.528 kg·m^2.

Example 2: A hollow sphere has a mass of 25 kg and a radius of 0.5 m. Calculate its moment of inertia.

Given:
– $M = 25 \text{ kg}$
– $R = 0.5 \text{ m}$

Substituting the values into the formula:
$I = \frac{2}{3}MR^2$
$I = \frac{2}{3}(25 \text{ kg})(0.5 \text{ m})^2$
$I = 2.083 \text{ kg}\cdot\text{m}^2$

Therefore, the moment of inertia of the hollow sphere is 2.083 kg·m^2.

Comparison with Solid Spheres

It is important to note that the moment of inertia of a hollow sphere is greater than that of a solid sphere with the same mass and radius. This is because the mass of a hollow sphere is distributed farther from the axis of rotation, which increases its resistance to rotational motion.

For a solid sphere, the moment of inertia formula is:

$I = \frac{2}{5}MR^2$

Comparing the two formulas, we can see that the moment of inertia of a hollow sphere is $\frac{2}{3}$ times the moment of inertia of a solid sphere with the same mass and radius.

Applications and Significance

The moment of inertia of a hollow sphere is an important concept in various fields, including:

1. Rotational Dynamics: The moment of inertia is a crucial parameter in the study of rotational motion, as it determines the object’s resistance to changes in angular velocity.

2. Mechanical Engineering: The moment of inertia is used in the design and analysis of rotating machinery, such as flywheels, gears, and turbines.

3. Astronomy: The moment of inertia of celestial bodies, such as planets and stars, is an important factor in understanding their rotational behavior and dynamics.

4. Sports and Recreation: The moment of inertia of sports equipment, such as balls and wheels, can affect their performance and handling characteristics.

Understanding the moment of inertia of a hollow sphere is essential for accurately predicting and analyzing the rotational behavior of various systems and objects.

Conclusion

The moment of inertia of a hollow sphere is a fundamental concept in classical mechanics, and its formula $I = \frac{2}{3}MR^2$ is derived by considering the sphere as a collection of infinitesimal mass elements. This formula is crucial for understanding the rotational dynamics of hollow spheres and their applications in various fields, such as engineering, astronomy, and sports. By mastering the concepts and examples presented in this guide, you will be well-equipped to tackle problems and analyses involving the moment of inertia of hollow spheres.

References

1. Lab Exp 02.docx – Experiment Title: Determine the moment of inertia of solid cylinder and sphere. Retrieved from https://www.coursehero.com/file/69341358/Lab-Exp-02docx/
2. Moment of Inertia for a hollow Sphere – Physics Forums. Retrieved from https://www.physicsforums.com/threads/moment-of-inertia-for-a-hollow-sphere.380715/
3. Moment of Inertia Of A Hollow Sphere – Expression, Derivation And … Retrieved from https://byjus.com/jee/moment-of-inertia-of-a-hollow-sphere/