The Microscope Resolution Limit Formula: A Comprehensive Guide for Physics Students

The microscope resolution limit formula is a fundamental principle in microscopy that quantifies the ability of a microscope to distinguish two nearby points in a specimen. This formula is a crucial tool for understanding the limitations and capabilities of various microscope designs, and it plays a vital role in the field of high-resolution imaging.

Understanding the Microscope Resolution Limit Formula

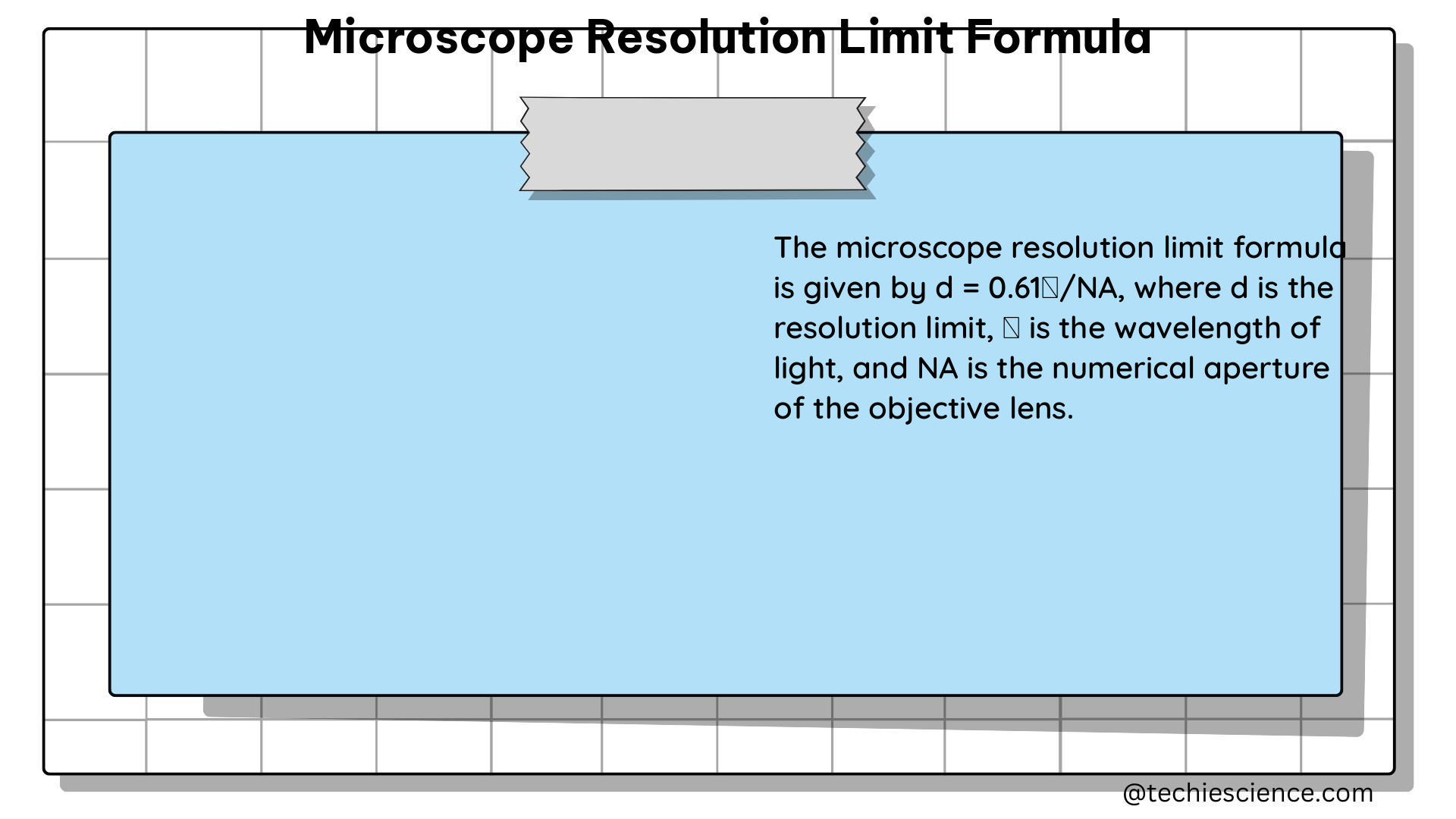
The microscope resolution limit formula is given by:

r = 0.61λ / NA

where:
– r is the resolution limit, which represents the minimum distance between two points in a specimen that can be distinguished as separate entities.
– λ is the wavelength of the light used for imaging.
– NA is the numerical aperture of the objective lens.

Numerical Aperture (NA)

The numerical aperture (NA) of an objective lens is a measure of its ability to collect light and is given by the formula:

NA = n * sin(α)

where:
– n is the refractive index of the medium between the lens and the specimen.
– α is the half-angle of the maximum cone of light that can enter the lens.

The numerical aperture is a crucial factor in determining the resolution limit of a microscope, as it directly affects the ability of the lens to gather light and resolve fine details.

Wavelength of Light (λ)

The wavelength of light used for imaging (λ) is another important factor in the microscope resolution limit formula. The wavelength of light can range from ultraviolet (UV) to infrared (IR), with visible light falling in the range of 400 to 700 nanometers (nm).

Generally, shorter wavelengths of light, such as UV or blue light, can provide higher resolution compared to longer wavelengths, such as red or infrared light. This is because the resolution limit is inversely proportional to the wavelength of light used for imaging.

Practical Considerations and Limitations

While the microscope resolution limit formula provides a theoretical framework for understanding the resolution capabilities of a microscope, there are several practical considerations and limitations that must be taken into account.

Diffraction and Aberrations

Diffraction and aberrations are two primary factors that can limit the achievable resolution of a microscope. Diffraction, which is the bending of light waves around the edges of an aperture, can introduce blurring and reduce the sharpness of the image. Aberrations, which are distortions in the optical system, can also degrade the image quality and limit the resolution.

Noise and Signal-to-Noise Ratio

The signal-to-noise ratio (SNR) is another important factor that can affect the ability to distinguish nearby points in a specimen. Noise, which can arise from various sources such as thermal fluctuations or electronic interference, can reduce the contrast and make it more difficult to resolve fine details.

Sampling Frequency and Pixel Size

The sampling frequency, which is related to the pixel size of the imaging sensor, can also impact the resolution. If the sampling frequency is too low, it can lead to aliasing and loss of high-frequency information, limiting the effective resolution of the microscope.

Improving Microscope Resolution

To achieve the highest possible resolution, it is essential to optimize the various factors that contribute to the microscope resolution limit. This can be accomplished through the following strategies:

1. Selecting Appropriate Objective Lenses: Choosing objective lenses with higher numerical apertures (NA) can significantly improve the resolution limit.
2. Utilizing Shorter Wavelengths of Light: Using light sources with shorter wavelengths, such as UV or blue light, can provide better resolution compared to longer wavelengths.
3. Minimizing Diffraction and Aberrations: Employing advanced optical design techniques and using high-quality optical components can help mitigate the effects of diffraction and aberrations.
4. Enhancing Signal-to-Noise Ratio: Improving the signal-to-noise ratio through techniques like signal averaging, noise reduction, and advanced image processing can enhance the ability to distinguish nearby points.
5. Optimizing Sampling Frequency: Ensuring an appropriate sampling frequency, in accordance with the Nyquist-Shannon sampling theorem, can help preserve high-frequency information and improve the effective resolution.

Advanced Microscopy Techniques

In addition to the strategies mentioned above, there are several advanced microscopy techniques that can further push the boundaries of resolution:

1. Confocal Microscopy: Confocal microscopy uses a focused laser beam and a pinhole to selectively illuminate and detect light from a specific focal plane, improving the resolution and contrast of the image.
2. Super-Resolution Microscopy: Techniques like Stimulated Emission Depletion (STED) microscopy, Structured Illumination Microscopy (SIM), and Single-Molecule Localization Microscopy (SMLM) can achieve resolutions beyond the diffraction limit of light.
3. Electron Microscopy: Electron microscopes, such as Scanning Electron Microscopes (SEM) and Transmission Electron Microscopes (TEM), can provide significantly higher resolutions compared to optical microscopes by using electron beams instead of light.

Practical Examples and Numerical Problems

To illustrate the application of the microscope resolution limit formula, let’s consider a few examples:

1. Example 1: Visible Light Microscope
2. Wavelength of light (λ): 550 nm
3. Numerical Aperture (NA): 1.25

4. Calculated Resolution Limit (r): r = 0.61 * 550 nm / 1.25 = 0.268 μm

5. Example 2: Ultraviolet (UV) Microscope

6. Wavelength of light (λ): 365 nm
7. Numerical Aperture (NA): 1.4

8. Calculated Resolution Limit (r): r = 0.61 * 365 nm / 1.4 = 0.158 μm

9. Numerical Problem: Improving Resolution by Increasing NA

10. Wavelength of light (λ): 500 nm
11. Initial Numerical Aperture (NA1): 1.0
12. Improved Numerical Aperture (NA2): 1.4
13. Initial Resolution Limit (r1): r1 = 0.61 * 500 nm / 1.0 = 0.305 μm
14. Improved Resolution Limit (r2): r2 = 0.61 * 500 nm / 1.4 = 0.218 μm
15. Percentage Improvement in Resolution: (r1 - r2) / r1 * 100 = 28.5%

These examples demonstrate the practical application of the microscope resolution limit formula and how various parameters, such as the wavelength of light and the numerical aperture, can be adjusted to improve the resolution of a microscope.

Conclusion

The microscope resolution limit formula is a fundamental principle in microscopy that provides a quantitative understanding of the ability of a microscope to distinguish nearby points in a specimen. By understanding the factors that contribute to the resolution limit, such as the numerical aperture and the wavelength of light, physicists and researchers can optimize their microscope systems to achieve the highest possible resolution for their specific applications.

Through the use of advanced microscopy techniques, such as confocal microscopy and super-resolution microscopy, the boundaries of resolution can be pushed even further, enabling the visualization of increasingly smaller and more intricate structures. By mastering the concepts and practical applications of the microscope resolution limit formula, physics students and researchers can unlock the full potential of microscopy and contribute to the advancement of scientific discovery.

References:

1. Microscope Resolution Explained Using Blood Cells. Microscope World. https://www.microscopeworld.com/p-3468-microscope-resolution-explained-using-blood-cells.aspx
2. Super-resolution Microscopy. Northwestern University. https://www.feinberg.northwestern.edu/sites/cam/docs/learning-resources/super-resolution-microscopy.pdf
3. Modulation Transfer Function. Nikon’s MicroscopyU. https://www.microscopyu.com/microscopy-basics/modulation-transfer-function
4. Principles of Optics. Born, M., & Wolf, E. (1980). Cambridge University Press.
5. Fundamentals of Photonics. Saleh, B. E., & Teich, M. C. (2019). John Wiley & Sons.