Methanol Density 2: A Comprehensive Guide for Physics Students

Summary

Methanol, a widely used chemical compound, has a well-defined density that is a fundamental property of the substance. Contrary to the query, the density of methanol is not 2, but rather approximately 792 kg/m³ (or 0.792 g/cm³) at standard temperature and pressure. This article delves into the technical details and provides a comprehensive understanding of methanol density for physics students.

Understanding Methanol Density

Methanol, also known as wood alcohol or methyl alcohol, is a simple organic compound with the chemical formula CH3OH. Its density is a crucial property that is widely used in various applications, such as in the chemical industry, fuel production, and scientific research.

Density as a Fundamental Property

The density of a substance is a fundamental property that does not change based on specific conditions, unless under extreme circumstances like high pressure or temperature. This means that the density of methanol at a given temperature and pressure is a fixed value that can be found in reference tables or determined through experiments.

Factors Affecting Methanol Density

The density of methanol can be influenced by several factors, including:

1. Temperature: As the temperature of methanol increases, its density typically decreases due to the expansion of the liquid.
2. Pressure: Increasing the pressure on methanol can slightly increase its density, as the molecules are compressed.
3. Purity: The presence of impurities or other substances mixed with methanol can affect its overall density.

Standard Methanol Density

At standard temperature and pressure (25°C or 298K, and 1 atmosphere or 101.3 kPa), the density of pure methanol is approximately 792 kg/m³ (or 0.792 g/cm³). This value is widely accepted and used as a reference in various calculations and applications.

Methanol Density Calculations

To calculate the density of methanol, you can use the following formula:

Density (ρ) = Mass (m) / Volume (V)

Where:
– Density (ρ) is measured in kg/m³ or g/cm³
– Mass (m) is measured in kilograms (kg) or grams (g)
– Volume (V) is measured in cubic meters (m³) or cubic centimeters (cm³)

Example Calculation

Let’s say you have 10 grams of pure methanol and you need to find its volume.

Given:
– Mass (m) = 10 g
– Density (ρ) = 0.792 g/cm³ (or 792 kg/m³)

To find the volume (V), we can rearrange the density formula:

Volume (V) = Mass (m) / Density (ρ)
Volume (V) = 10 g / 0.792 g/cm³
Volume (V) = 12.63 cm³

Therefore, 10 grams of pure methanol has a volume of 12.63 cubic centimeters (cm³).

Methanol Density Measurement Techniques

There are several methods to measure the density of methanol, including:

1. Pycnometry: This technique involves measuring the mass of a known volume of methanol using a calibrated pycnometer.
2. Hydrometry: Hydrometric methods, such as using a hydrometer, can determine the density of methanol by measuring its buoyancy in the liquid.
3. Oscillating U-tube: This method uses an oscillating U-shaped tube filled with methanol to determine its density based on the oscillation frequency.
4. Displacement: The displacement method involves measuring the volume of methanol displaced by a known mass of the liquid.

Each of these techniques has its own advantages and limitations, and the choice of method depends on the specific requirements of the application and the available equipment.

Methanol Density Applications

The density of methanol is an important property that is widely used in various applications, including:

1. Chemical Industry: Methanol is a versatile chemical used in the production of formaldehyde, acetic acid, and other chemicals, where its density is a crucial parameter.
2. Fuel Production: Methanol can be used as a fuel or fuel additive, and its density is a key factor in fuel blending and engine performance calculations.
3. Scientific Research: In scientific experiments and analyses, the density of methanol is often required for accurate calculations and data interpretation.
4. Environmental Studies: The density of methanol is relevant in environmental studies, such as understanding its behavior and transport in water bodies or soil.

Methanol Density Numerical Problems

Here are a few numerical problems to help you practice your understanding of methanol density:

1. Problem: A sample of pure methanol has a mass of 50 grams. Calculate the volume of the sample, given that the density of methanol is 792 kg/m³.

Solution:
– Given: Mass (m) = 50 g, Density (ρ) = 792 kg/m³
– To find: Volume (V)
– Using the density formula: Density (ρ) = Mass (m) / Volume (V)
– Rearranging the formula: Volume (V) = Mass (m) / Density (ρ)
– Substituting the values: Volume (V) = 50 g / (792 kg/m³)
– Converting the units: Volume (V) = 0.063 m³ or 63 liters

1. Problem: A container has a volume of 1 liter and is filled with pure methanol. Calculate the mass of the methanol in the container.

Solution:
– Given: Volume (V) = 1 liter = 0.001 m³, Density (ρ) = 792 kg/m³
– To find: Mass (m)
– Using the density formula: Density (ρ) = Mass (m) / Volume (V)
– Rearranging the formula: Mass (m) = Density (ρ) × Volume (V)
– Substituting the values: Mass (m) = 792 kg/m³ × 0.001 m³
– Mass (m) = 0.792 kg or 792 grams

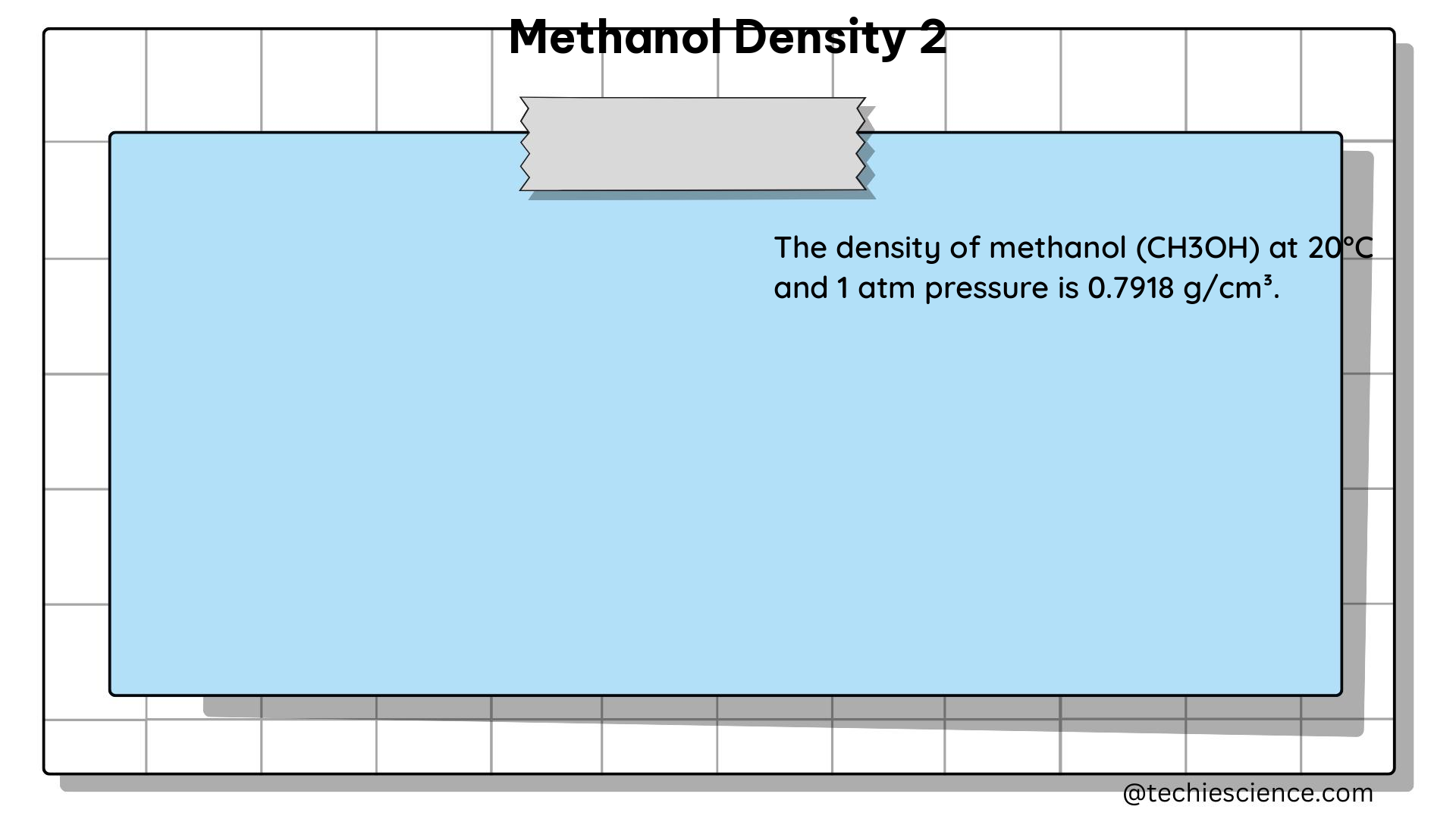
1. Problem: The density of methanol at 20°C is 0.7918 g/cm³. Calculate the mass of 500 milliliters of methanol at this temperature.

Solution:
– Given: Volume (V) = 500 mL = 0.5 L, Density (ρ) = 0.7918 g/cm³
– To find: Mass (m)
– Using the density formula: Density (ρ) = Mass (m) / Volume (V)
– Rearranging the formula: Mass (m) = Density (ρ) × Volume (V)
– Substituting the values: Mass (m) = 0.7918 g/cm³ × 0.5 L
– Converting the units: Mass (m) = 395.9 g

These problems demonstrate the application of the density formula and the conversion of units to calculate the mass or volume of methanol given its density.

Conclusion

In conclusion, the density of methanol is a fundamental property that is well-defined and widely used in various applications. Contrary to the initial query, the density of methanol is not 2, but rather approximately 792 kg/m³ (or 0.792 g/cm³) at standard temperature and pressure. This article has provided a comprehensive guide for physics students, covering the technical details, calculation methods, measurement techniques, and applications of methanol density.

References

[A] Density of methanol: https://www.engineeringtoolbox.com/methanol-density-d_1302.html
[B] Methanol properties: https://www.nist.gov/pml/chemical-thermodynamics-data-center/compendium-chemical-thermodynamic-properties-fluids-second
[C] Methanol density calculation: https://www.calculatoratoz.com/en/methanol-density-calculator/Calculate-Methanol-Density
[D] Methanol density measurement techniques: https://www.sciencedirect.com/topics/engineering/methanol-density