This article discusses about mass flow rate and pressure. They both have a direct relation between them (although no direct formula). Lets study more about it.
Anything which flows is bound to have certain mass. The amount of mass which passes through a point per second is called as mass flow rate. The term mass flow rate finds its use in thermal engineering and fluid mechanics. Lets discuss more about mass flow rate in this article.
What is pressure?
Pressure is the amount of force exerted per unit area. For the same amount of force, if the area is smaller then value of pressure is more and if the area is more then the value of pressure is less.
The units of pressure is N/m^2. Mathematically, pressure can be given by-
P = F/A
Where,
F is the force applied normal to the cross section
A is the area of the cross section
What is mass flow rate?
The term flow means anything pertaining to movement. Mass flow rate refers to an amount of mass passing through a point per second. The mass can be of anything such as gas, water, oil or any other fluid.
The term mass flow rate is very important term used in fluid mechanics and thermal engineering. Its applications lie in turbo machinery, rockets, aeroplane and many other fluid related applications. Mathematically, mass flow rate can be given as,
Mass flow rate and pressure relation
Logically, more the pressure applied to the inlet section will mean more pressure difference is created between inlet and outlet hence more mass will try to rush through the section. Hence, we can say that mass flow rate is directly proportional to pressure (gradient).
Even vice versa is true, when more mass flows through a point per second then the force exerted by the mass molecules on the surface of the section will be greater hence pressure will be more if mass flow rate is more. Hence we can say both are directly proportional to each other. Note that this completely true for incompressible fluids like water.
Does mass flow rate change with pressure?
Note that alone pressure has no effect on mass flow rate, it is the pressure difference created that affects the flow rate.
The value of pressure difference between the inlet section and outlet section affects the mass flow rate. If the pressure difference is more then the mass flow rate will be more and if the pressure difference will be less then the mass flow rate will be less.
Alone greater pressure has no effect on the flow rate, if both the inlet and outlet has high value of pressures and low difference between them then the flow rate will be low due to low pressure difference. We will get more clarity by looking at an example.
Mass flow rate and pressure difference relation example
As discussed in earlier section, pressure difference directly affects the mass flow rate. This can be explained using simple example discussed below.
The aeroplane will generate more lift when there is a larger pressure difference (as in cambered airfoils). If there is large pressure values on both the sides of airfoil then there won’t be any significant change in pressure values and thus no or very less pressure difference will be there. Due to this very less air will flow hence generating lesser lift.
Bernoulli’s equation
The Bernoulli’s principle is meant for incompressible fluids which states that when a fluid is flowing in a streamline flow then velocity increases with decrease in static pressure.
In simple terms, Bernoulli’s principle means- Static pressure+Dynamic pressure= Total pressure and that is said to be constant.
Mathematically, Bernoulli’s principle can be given as-
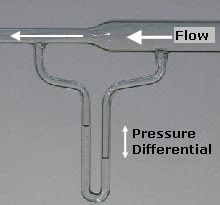
Image credits: user:ComputerGeezer and Geof, VenturiFlow, CC BY-SA 3.0
Hagen Poisueille law
This law given the direct relation between pressure difference and the volumetric flow rate.
This law gives the relation for pressure drop for incompressible Newtonian fluids in a laminar flow. The Hagen Poisueille equation is given as follows-
What are the different types flow?
There are three main types of flows- Laminar, turbulent and transient flow.
Laminar flow
This type of flow is characterized by fluid particles flowing in a smooth manner. Each layer moves past the adjacent layer in such a manner that they don’t mix. We can tell whether the flow is laminar or not by looking at the value of Reynold’s number of the flow. Reynold’s number is discussed in later sections of this article.
Turbulent flow
This type of layer is characterized by mixing of two fluid layers in a flow. The flow is more violent than laminar flow. It is desired when mixing of two fluids is to be done.
Transient flow
Transient flow is simply the transition between laminar and turbulent flow.
Reynold’s number
Reynold’s number is dimensionless number which is used for determining the type of flow in the system.
The ratio of inertial forces to viscous forces is called as Reynold’s number. The general formula for Reynold’s number is given below-
where,
mu is the dynamic viscosity
V is the velocity of flow
Significance of Reynold’s number
As discussed in above section, Reynold’s number is used to find the type of flow in the system. It gives us an idea about the inertial and viscous effects of flow on the system.
For fluid flowing over a flat plate-
- Laminar flow- Re<3×10^5
- Turbulent flow- Re>3×10^5
For fluid in a circular pipe-
- Laminar flow- Re<2000
- Turbulent flow-Re>4000
- Transient flow-2000<Re<4000
Prandtl number
Prandtl number is named after the physicist Ludwig Prandtl. It is a dimensionless number which is used for determining the behaviour of heat transfer.
Prandtl number is the ratio of momentum diffusivity to thermal diffusivity. The mass analog of Prandtl number is Schmidt number. Mathematically, it can be written as-
Cp is the specific heat at constant pressure
k is the thermal conductivity
Mass flow rate example
Let us assume following data for a system.
Density of the fluid- 0.2 kg/m^3
Area of the cross section- 1m^2
Volume flow rate- 10m^3/s
Use the following data to calculate the mass flow rate in the system.
Mass flow rate can be found using the formula given below-
From using the formula given above, we get mass flow rate as- 2kg/s.
Hi ….I am Abhishek Khambhata, have pursued B. Tech in Mechanical Engineering. Throughout four years of my engineering, I have designed and flown unmanned aerial vehicles. My forte is fluid mechanics and thermal engineering. My fourth-year project was based on the performance enhancement of unmanned aerial vehicles using solar technology. I would like to connect with like-minded people.