Mastering the Lensmaker’s Equation: A Comprehensive Guide for Physics Students

The lensmaker’s equation is a fundamental principle in optics that allows us to calculate the focal length of a lens based on its curvature, thickness, and refractive index. This equation is a crucial tool for designing and understanding various types of lenses, from simple to complex, and is essential knowledge for physics students.

Understanding the Lensmaker’s Equation

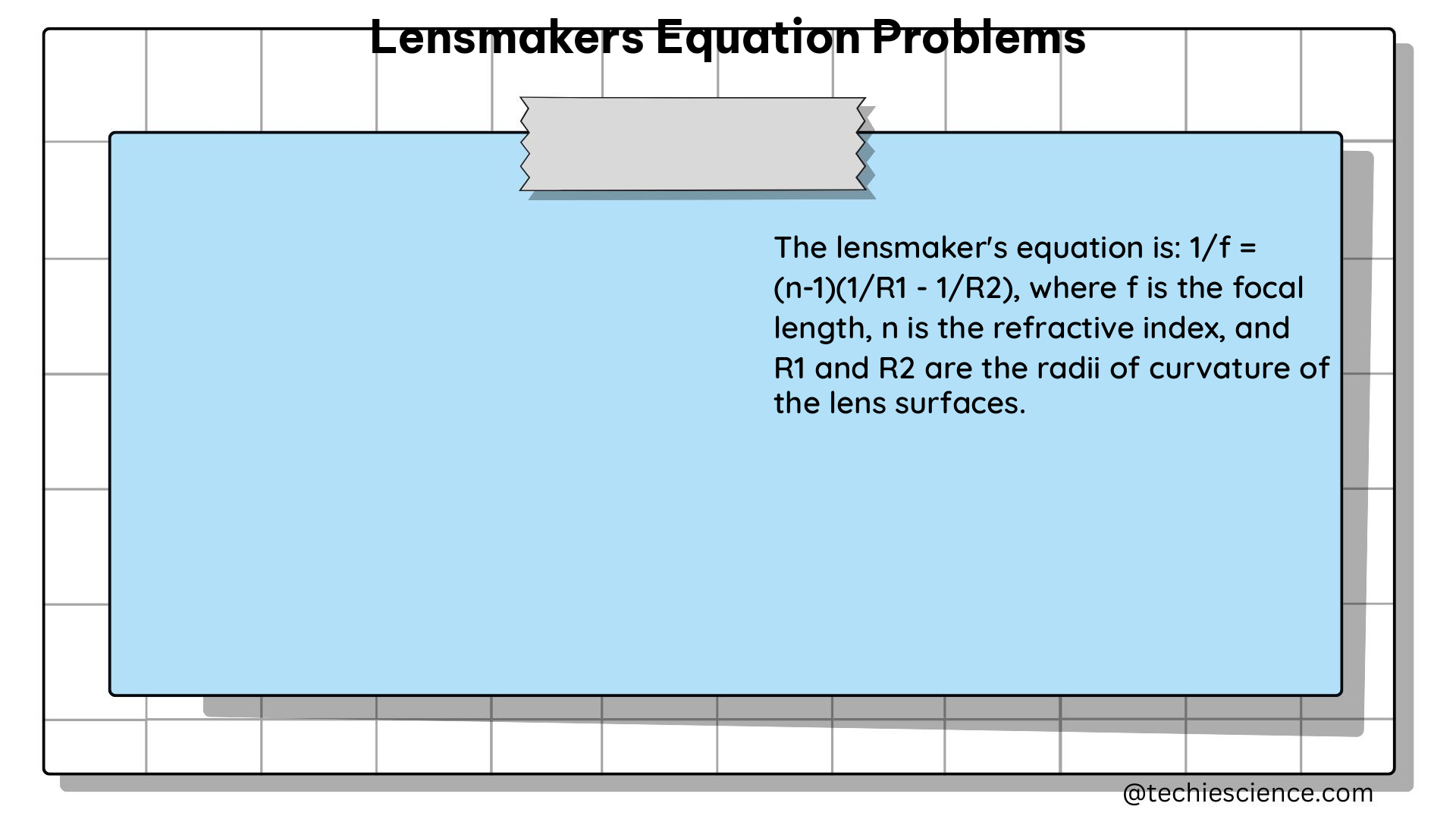
The lensmaker’s equation is given by the formula:

1/f = (n-1) ⋅ [(1/R1) – (1/R2) + {[(n-1)d]/(n⋅R1⋅R2)}]

Where:
– f is the focal length of the lens
– n is the refractive index of the lens material
– R1 and R2 are the radii of curvature of the two surfaces of the lens
– d is the thickness of the lens

The sign convention used in this equation is crucial to understand. A positive radius, R, occurs when the center of curvature is further along in the path of the light ray, while a negative radius, R, occurs when the rays have already passed by the center of the surface of curvature. Convex lenses, which converge light, have a positive radius of curvature, while concave lenses, which diverge light, have a negative radius of curvature.

Lens Types and the Lensmaker’s Equation

The lensmaker’s equation can be used to design a variety of simple and complex lenses, including:

1. Double-Convex or Double-Concave Lenses:
2. In a double-convex lens, both surfaces have a positive radius of curvature (R1 and R2 are positive).

3. In a double-concave lens, both surfaces have a negative radius of curvature (R1 and R2 are negative).

4. Meniscus Lenses:

5. A meniscus lens has one convex and one concave surface.

6. The lensmaker’s equation can be used to design meniscus lenses by considering the different signs of R1 and R2.

7. Plano-Convex or Plano-Concave Lenses:

8. A plano-convex lens has one flat (plano) surface and one convex surface.
9. A plano-concave lens has one flat (plano) surface and one concave surface.
10. In these cases, one of the radii of curvature (R1 or R2) is infinite, simplifying the lensmaker’s equation.

Numerical Examples and Problem-Solving

To better understand the application of the lensmaker’s equation, let’s consider some numerical examples:

Example 1: Calculating the Focal Length of a Double-Convex Lens
Given:
– Refractive index (n) = 1.5
– Radius of curvature of the first surface (R1) = 10 cm
– Radius of curvature of the second surface (R2) = 15 cm
– Thickness of the lens (d) = 0.5 cm

Using the lensmaker’s equation:
1/f = (n-1) ⋅ [(1/R1) – (1/R2) + {[(n-1)d]/(n⋅R1⋅R2)}]
1/f = (1.5-1) ⋅ [(1/10) – (1/15) + {[(1.5-1)0.5]/(1.5⋅10⋅15)}]
1/f = 0.5 ⋅ [0.1 – 0.0667 + 0.0111]
1/f = 0.0444
f = 22.5 cm

Example 2: Calculating the Focal Length of a Plano-Convex Lens
Given:
– Refractive index (n) = 1.6
– Radius of curvature of the convex surface (R1) = 20 cm
– Thickness of the lens (d) = 0.3 cm

Using the lensmaker’s equation:
1/f = (n-1) ⋅ [(1/R1) – (1/∞) + {[(n-1)d]/(n⋅R1⋅∞)}]
1/f = (1.6-1) ⋅ [(1/20) – 0 + {[(1.6-1)0.3]/(1.6⋅20⋅∞)}]
1/f = 0.6 ⋅ [0.05 + 0]
1/f = 0.03
f = 33.33 cm

These examples demonstrate how the lensmaker’s equation can be applied to calculate the focal length of various lens types, considering their curvature, thickness, and refractive index.

Limitations and Considerations

When using the lensmaker’s equation, it’s important to consider the following limitations and factors:

1. Refractive Index Variation in the Human Crystalline Lens:
2. The refractive index of the human crystalline lens varies with age, ranging from a maximum of 1.42 at the core to a minimum of 1.37 at the surface.

3. Using a constant equivalent refractive index can lead to slight errors in the estimation of lens power, depending on the age of the individual.

4. Thin Lens Approximation:

5. The lensmaker’s equation is derived under the thin lens approximation, which assumes that the lens thickness is much smaller than the radii of curvature.

6. For thicker lenses, the equation may not provide accurate results, and more advanced models may be required.

7. Chromatic Aberration:

8. The lensmaker’s equation assumes a single, fixed refractive index for the lens material.
9. In reality, the refractive index of a lens material can vary with the wavelength of light, leading to chromatic aberration, which must be considered in lens design.

By understanding these limitations and considerations, physics students can effectively apply the lensmaker’s equation to solve a wide range of problems and design various types of lenses for different applications.

Conclusion

The lensmaker’s equation is a fundamental tool in optics that allows us to calculate the focal length of a lens based on its curvature, thickness, and refractive index. By mastering this equation and understanding its applications, physics students can gain a deeper understanding of lens design and the behavior of light in various optical systems.

References:

1. Lensmaker’s Equation – StatPearls – NCBI Bookshelf. (2023-07-08). Retrieved from https://www.ncbi.nlm.nih.gov/books/NBK594278/
2. Lensmaker’s Equation Example # 1 – AK Lectures. Retrieved from https://aklectures.com/lecture/thin-lenses-and-lensmaker%27s-equation/lensmakers-equation-example-1
3. Lenses Mini Report (docx) – Course Sidekick. Retrieved from https://www.coursesidekick.com/physics/2040971
4. The Mathematics of Lenses – The Physics Classroom. Retrieved from https://www.physicsclassroom.com/class/refrn/Lesson-5/The-Mathematics-of-Lenses
5. Lens Maker Equation Problem, Plano-Convex Lens – YouTube. Retrieved from https://www.youtube.com/watch?v=-oXqTkaDUpU