Mastering Lens Virtual Image Problems: A Comprehensive Guide

Lens virtual image problems are a fundamental concept in optics, where the formation and characteristics of virtual images created by lenses are studied. Understanding these problems is crucial for various applications, from photography and microscopy to optical instrument design. In this comprehensive guide, we will delve into the intricacies of lens virtual image problems, providing you with a thorough understanding of the underlying principles, formulas, and practical examples.

Understanding Lens Virtual Images

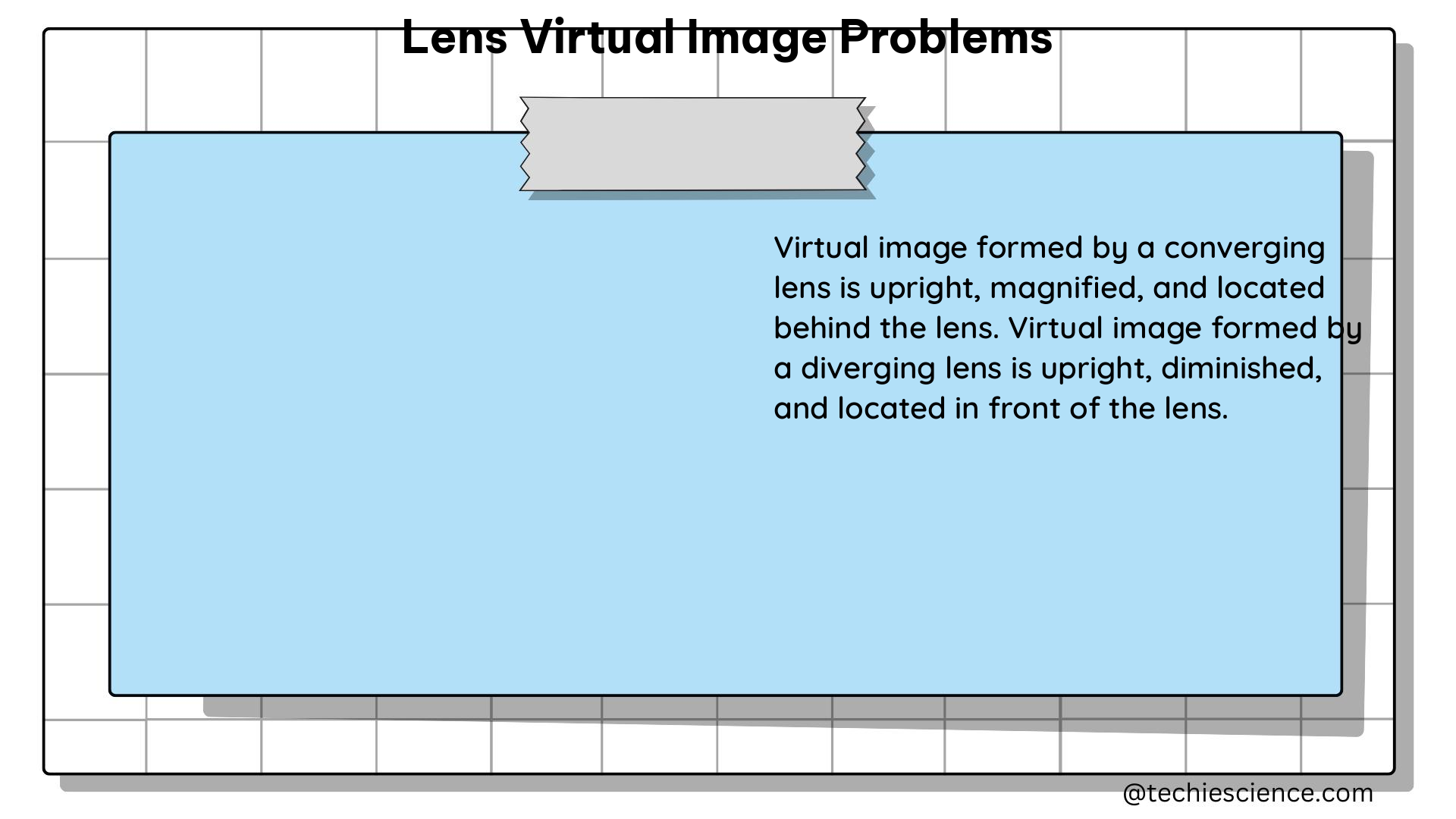
A virtual image is an image that appears to be formed behind a lens, but it cannot be projected onto a screen. Unlike real images, virtual images cannot be captured directly, but they can be observed by the human eye. The formation of virtual images is governed by the properties of the lens, such as its focal length and the position of the object relative to the lens.

Thin Lens Equation

The relationship between the object distance (do), image distance (di), and focal length (f) of a lens is described by the thin lens equation:

1/do + 1/di = 1/f

This equation is fundamental in understanding the formation of virtual images and can be used to determine the characteristics of the image, such as its position, size, and orientation.

Types of Lenses

Lenses can be classified into two main categories: converging (or positive) lenses and diverging (or negative) lenses. The type of lens used plays a crucial role in the formation of virtual images.

Converging Lenses

Converging lenses are thicker at the center than at the edges and have a positive focal length. They can form both real and virtual images, depending on the position of the object relative to the lens.

Diverging Lenses

Diverging lenses are thinner at the center than at the edges and have a negative focal length. They always form virtual images, regardless of the object’s position.

Virtual Image Formation with Diverging Lenses

When an object is placed in front of a diverging lens, a virtual image is always formed. The image is located on the same side of the lens as the object and is smaller than the object.

Example 1: Virtual Image with a Diverging Lens

Let’s consider the following example:

• Object Distance (do): 15 cm
• Focal Length (f): -8.2 cm
• Image Distance (di): -5.3 cm (negative, indicating a virtual image)

In this case, the image distance is negative, which means the image is located on the same side of the lens as the object, indicating a virtual image. The image is also smaller than the object, as the absolute value of the image distance is less than the object distance.

Virtual Image Formation with Converging Lenses

Converging lenses can form both real and virtual images, depending on the position of the object relative to the lens.

Example 5: Virtual Image with a Converging Lens

Let’s consider another example:

• Object Distance (do): 6 cm
• Focal Length (f): 10 cm
• Image Distance (di): -15 cm (negative, indicating a virtual image)

In this case, the object is placed between the lens and its focal point, resulting in a virtual image. The image distance is negative, indicating that the image is located on the same side of the lens as the object.

Real Image Formation with Converging Lenses

When an object is placed beyond the focal point of a converging lens, a real image is formed on the opposite side of the lens.

Example 2: Real Image with a Converging Lens

Let’s consider the following example:

• Object Distance (do): 22 m
• Focal Length (f): 8 m
• Image Distance (di): 12.57 m (positive, indicating a real image)

In this case, the object is placed beyond the focal point of the lens, resulting in a real image. The image distance is positive, indicating that the image is located on the opposite side of the lens from the object.

Image Characteristics

In addition to the position of the image, the size and orientation of the image are also important characteristics to consider.

Image Height

The height of the image (hi) can be calculated using the following formula:

hi = -do * hi / do

where hi is the object height and do is the object distance.

Example 3: Virtual Image with a Diverging Lens (Continued)

Continuing the previous example:

• Object Distance (do): 35.5 cm
• Focal Length (f): -12.2 cm
• Image Distance (di): -9.08 cm (negative, indicating a virtual image)
• Image Height (hi): -4.00 cm * (-9.08 cm) / (35.5 cm) = -1.01 cm (negative, indicating an inverted image)

In this case, the image height is negative, indicating that the image is inverted compared to the object.

Example 4: Real Image with a Converging Lens

Let’s consider another example:

• Object Distance (do): 8.30 cm
• Focal Length (f): 15.2 cm
• Image Distance (di): 18.3 cm (positive, indicating a real image)
• Image Height (hi): -4.00 cm * (-18.3 cm) / (8.30 cm) = 8.81 cm (positive, indicating an upright image)

In this case, the image height is positive, indicating that the image is upright compared to the object.

Practical Applications

Lens virtual image problems have numerous practical applications in various fields, including:

1. Photography: Understanding virtual image formation is crucial in the design and use of camera lenses, which can create both real and virtual images.
2. Microscopy: Microscopes often use converging lenses to form real images of small objects, which are then magnified and observed by the user.
3. Telescopes: Telescopes employ a combination of lenses and mirrors to create virtual and real images of distant objects, allowing for magnification and observation.
4. Optical Instruments: The principles of lens virtual image formation are applied in the design and development of various optical instruments, such as eyeglasses, magnifying glasses, and projectors.

Conclusion

Lens virtual image problems are a fundamental concept in optics, and understanding them is crucial for various applications. In this comprehensive guide, we have explored the underlying principles, formulas, and practical examples related to the formation and characteristics of virtual images created by lenses. By mastering these concepts, you will be well-equipped to tackle complex problems in optics and apply your knowledge to real-world scenarios.

Reference:

1. Hecht, E. (2016). Optics (5th ed.). Pearson.
2. Serway, R. A., & Jewett, J. W. (2018). Physics for Scientists and Engineers with Modern Physics (10th ed.). Cengage Learning.
3. Sears, F. W., Zemansky, M. W., Young, H. D., & Freedman, R. A. (2019). University Physics with Modern Physics (15th ed.). Pearson.