Why is voltage the same in parallel combination?
When it comes to understanding electrical circuits, one of the fundamental concepts to grasp is voltage. Voltage is the driving force that pushes electric charges through a circuit, and it plays a crucial role in determining how electrical components behave. In a parallel combination of components, such as resistors, capacitors, or inductors, the voltage remains the same across each component. This phenomenon is known as voltage consistency in parallel circuits.
Explanation using the analogy of water leaking from a bucket with pipes
To better understand why voltage remains the same in parallel circuits, let’s consider an analogy involving water. Imagine you have a bucket filled with water, and it has multiple pipes connected to it. Each pipe represents a component in the circuit. Now, if there is a leak in one of the pipes, the water will flow out of that pipe. However, the water level in the bucket remains the same, unaffected by the leak. Similarly, in a parallel circuit, the voltage remains constant across each component, just like the water level in the bucket.
Comparison with voltage in series circuits
To further emphasize the significance of voltage consistency in parallel circuits, let’s compare it with series circuits. In a series circuit, the components are connected one after another, forming a single path for the current to flow. In this configuration, the voltage is divided among the components based on their resistance. The voltage drop across each component adds up to the total voltage supplied by the source. However, in a parallel circuit, the voltage across each component remains the same, regardless of their individual resistances.
Explanation of voltage drop across resistors in parallel
In a parallel combination of resistors, each resistor provides a separate path for the current to flow. As a result, the voltage across each resistor remains constant. This can be explained using Kirchhoff’s voltage law, which states that the sum of the voltage drops across all components in a closed loop is equal to the applied voltage. In a parallel circuit, the voltage drop across each resistor is equal to the applied voltage, ensuring voltage consistency across the resistors.
Importance of parallel circuits in maintaining voltage consistency
Parallel circuits play a crucial role in maintaining voltage consistency in various electrical systems. By connecting components in parallel, engineers can ensure that each component receives the same voltage, regardless of their individual characteristics. This is particularly important in applications where voltage-sensitive devices are used, such as in electronic devices or power distribution systems. Parallel circuits allow for efficient voltage division, ensuring that each component operates at its optimal voltage level.
Why is voltage the same in parallel combination of capacitors?
In electronic circuits, capacitors are commonly used to store and release electrical energy. When multiple capacitors are connected in parallel, they share the same voltage. This phenomenon occurs due to the fundamental principles of electrical circuits and the behavior of capacitors. Let’s explore the reasons behind this phenomenon and understand its applications in electronic circuits.
Explanation of voltage distribution in parallel capacitors
When capacitors are connected in parallel, their positive terminals are connected together, and their negative terminals are connected together. This configuration allows the flow of current to divide among the capacitors based on their capacitance values. However, the voltage across each capacitor remains the same.
To understand this, let’s consider a simple analogy. Imagine a water pipe connected to multiple containers. Each container has a different capacity to hold water. When water flows through the pipe, it distributes itself among the containers based on their capacity. However, the water level in each container remains the same.
Similarly, in a parallel combination of capacitors, the voltage across each capacitor remains constant. This is because the voltage represents the potential difference between the positive and negative terminals of a component. Since the positive and negative terminals of capacitors in parallel are connected together, the potential difference across them is the same.
Capacitors in parallel share the same voltage
The reason why capacitors in parallel share the same voltage can be explained by Kirchhoff’s voltage law. According to this law, the sum of the voltages in a closed loop of an electrical circuit is equal to zero.
In the case of capacitors in parallel, the voltage across each capacitor can be considered as a loop. Since the voltage across each capacitor is the same, the sum of these voltages will be zero. This implies that the voltage across each capacitor in parallel is equal.
Application of parallel capacitors in electronic circuits
The fact that capacitors in parallel share the same voltage has practical implications in electronic circuits. One of the main applications is voltage division. By connecting capacitors in parallel, we can divide the voltage across a circuit into smaller voltages across individual capacitors.
This voltage division technique is often used in power supply circuits to provide different voltage levels to different components. By carefully selecting the capacitance values of the parallel capacitors, we can achieve the desired voltage division ratio.
Another application of parallel capacitors is in filtering circuits. Capacitors are commonly used to filter out unwanted noise or ripple in a circuit. By connecting capacitors in parallel, we can increase the overall capacitance and improve the filtering efficiency.
How is voltage the same in a parallel circuit?
When it comes to understanding electrical circuits, one important concept to grasp is how voltage behaves in parallel circuits. In a parallel circuit, multiple components are connected side by side, allowing the current to split and flow through each component independently. But what about voltage? Is voltage the same in parallel circuits? Let’s explore this question in more detail.
Description of parallel circuits and their characteristics
Before delving into the specifics of voltage in parallel circuits, let’s first understand what a parallel circuit is and its characteristics. In a parallel circuit, the components are connected in such a way that there are multiple paths for the current to flow. Each component has its own branch, and the total current entering the circuit is divided among these branches.
One key characteristic of parallel circuits is that the voltage across each component remains the same. This means that regardless of the individual resistance, whether it’s a resistor, capacitor, or inductor, the voltage across each component connected in parallel will be equal.
Analysis of voltage distribution in parallel circuits
To understand why voltage remains the same in parallel circuits, we need to consider Kirchhoff’s Voltage Law (KVL). KVL states that the sum of the voltage drops across all components in a closed loop is equal to the applied voltage. In a parallel circuit, each component has its own closed loop, and according to KVL, the sum of the voltage drops across each component should equal the applied voltage.
Since the voltage across each component in a parallel circuit is the same, it follows that the sum of the voltage drops across all components will also equal the applied voltage. This ensures that voltage remains consistent throughout the parallel circuit.
Calculation of equivalent resistance in parallel circuits
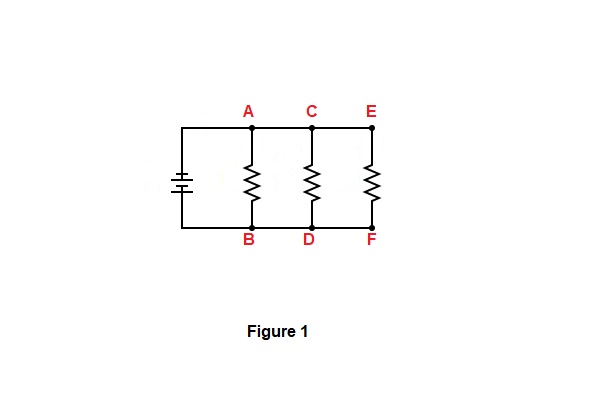
Another important aspect to consider in parallel circuits is the calculation of the equivalent resistance. The equivalent resistance is the single resistance value that would produce the same total current as the combination of all the parallel components.
To calculate the equivalent resistance in a parallel circuit, we use the formula:
1/Req = 1/R1 + 1/R2 + 1/R3 + ...
Where Req is the equivalent resistance and R1, R2, R3, etc., are the resistances of the individual components connected in parallel.
By calculating the equivalent resistance, we can determine the total current flowing through the parallel circuit. However, it’s important to note that even though the current may vary across each component, the voltage remains the same.
Demonstration of voltage consistency in parallel circuits
To further illustrate the concept of voltage consistency in parallel circuits, let’s consider a simple example. Imagine a parallel circuit consisting of three resistors: R1, R2, and R3. If we apply a voltage of 12 volts across the circuit, the voltage across each resistor will also be 12 volts.
Voltage across R1 = 12 volts
Voltage across R2 = 12 volts
Voltage across R3 = 12 volts
This example demonstrates that regardless of the individual resistance values, the voltage across each component in a parallel circuit remains the same.
Is voltage the same in parallel circuits according to Reddit?
When it comes to understanding electrical circuits, one question that often arises is whether the voltage remains the same in parallel circuits. To shed light on this topic, we turn to the discussions on Reddit, where users share their opinions and explanations. Let’s delve into the insights provided by the Reddit community regarding voltage in parallel circuits.
Overview of discussions on Reddit regarding voltage in parallel circuits
Reddit, being a platform for diverse perspectives, offers a wealth of discussions on various subjects, including electrical circuits. When it comes to voltage in parallel circuits, Redditors have engaged in lively conversations, sharing their knowledge and experiences.
Opinions and explanations from Reddit users
Many Reddit users have shared their opinions and explanations regarding voltage in parallel circuits. Some users emphasize that in an ideal scenario, where there are no resistances or losses, the voltage across parallel components remains the same. This concept aligns with Kirchhoff’s voltage law in parallel circuits, which states that the sum of the voltage drops across the parallel components equals the applied voltage.
Others have pointed out that in real-world scenarios, there may be slight variations in voltage due to factors such as resistance, impedance, or the presence of non-ideal components. These variations can lead to voltage drops in parallel circuits.
Consensus on voltage consistency in parallel circuits
While there may be slight variations in voltage due to real-world factors, the consensus among Reddit users is that the voltage across parallel components remains relatively consistent. This consensus is based on the understanding that, in an ideal scenario, the voltage across parallel components is the same.
To further illustrate this concept, let’s consider a simple example. Suppose we have two resistors connected in parallel to a power source. According to the consensus on Reddit, the voltage across both resistors would be the same, assuming no significant resistance or impedance.
Is voltage the same in parallel resistors?
When it comes to understanding electrical circuits, one fundamental concept is the distribution of voltage. In parallel resistor circuits, where multiple resistors are connected side by side, a common question arises: is the voltage the same across each resistor? In this section, we will explore the behavior of voltage in parallel resistor circuits and shed light on this intriguing question.
Explanation of voltage distribution in parallel resistors
To comprehend the distribution of voltage in parallel resistor circuits, we need to delve into the concept of Kirchhoff’s voltage law. According to this law, the sum of the voltages across all components in a closed loop is equal to zero. In the case of parallel resistors, each resistor forms a separate loop, allowing us to analyze the voltage distribution across them individually.
When resistors are connected in parallel, the voltage across each resistor is indeed the same. This is due to the fact that the voltage source connected to the circuit provides a constant potential difference, which is distributed equally across all the parallel branches. Therefore, regardless of the value of the resistors, the voltage across each one remains constant.
Analysis of voltage drop across parallel resistors
While the voltage across parallel resistors remains the same, the current flowing through each resistor may differ. This is a consequence of Ohm’s law, which states that the current flowing through a resistor is inversely proportional to its resistance. As a result, resistors with lower resistance will allow more current to pass through them compared to resistors with higher resistance.
To illustrate this, let’s consider a simple example. Suppose we have two resistors connected in parallel: R1 with a resistance of 2 ohms and R2 with a resistance of 4 ohms. If a voltage of 12 volts is applied across the circuit, the current flowing through R1 can be calculated using Ohm’s law: I = V/R. Thus, I1 = 12/2 = 6 amps. Similarly, the current flowing through R2 can be calculated as I2 = 12/4 = 3 amps.
Demonstration of voltage consistency in parallel resistor circuits
To further solidify our understanding, let’s conduct a practical demonstration using a simple circuit setup. We will connect three resistors in parallel and measure the voltage across each one.
- Gather the necessary materials: three resistors of different values, a power supply, and a voltmeter.
- Connect the resistors in parallel by connecting one terminal of each resistor to the positive terminal of the power supply and the other terminal to the negative terminal.
- Measure the voltage across each resistor using the voltmeter.
- Repeat the measurement multiple times and observe that the voltage across each resistor remains constant.
This experiment confirms that the voltage across parallel resistors is indeed the same, regardless of the individual resistor values. It showcases the consistent distribution of voltage in parallel resistor circuits.
Is voltage the same across resistors in parallel?
When it comes to understanding electrical circuits, one important concept to grasp is how voltage behaves in parallel resistor circuits. In this section, we will delve into the topic of voltage distribution in parallel resistor circuits and analyze the voltage drop across parallel resistors.
In a parallel circuit, multiple components are connected side by side, allowing the current to split and flow through each component independently. One common question that arises is whether the voltage across each resistor in a parallel circuit remains the same. Let’s explore this further.
Explanation of voltage distribution in parallel resistor circuits
In a parallel circuit, the voltage across each resistor is indeed the same. This can be attributed to the fact that the voltage across any two points in a circuit is determined by the electric potential difference between those points. Since the points connected to each resistor in a parallel circuit are at the same potential, the voltage across each resistor is equal.
To better understand this concept, let’s consider a simple example. Imagine a parallel circuit with three resistors connected to a power source. The voltage supplied by the power source is distributed equally across each resistor. This means that if the power source provides 12 volts, each resistor will have a voltage drop of 12 volts across it.
Analysis of voltage drop across parallel resistors
To analyze the voltage drop across parallel resistors, we can use Kirchhoff’s Voltage Law (KVL) in parallel circuits. According to KVL, the sum of the voltage drops across all components in a closed loop is equal to the applied voltage.
In a parallel circuit, each resistor forms a separate loop. Since the voltage across each resistor is the same, the sum of the voltage drops across all the resistors in a parallel circuit will be equal to the applied voltage.
Confirmation of voltage consistency across parallel resistors
To confirm the consistency of voltage across parallel resistors, we can also use the concept of equivalent voltage in parallel circuits. When resistors are connected in parallel, the reciprocal of their resistances is added together to determine the equivalent resistance of the parallel combination.
By applying Ohm’s Law (V = IR) to the equivalent resistance, we can calculate the current flowing through the parallel circuit. Since the current is the same across all resistors in a parallel circuit, the voltage drop across each resistor will be the same as well.
By understanding the behavior of voltage in parallel circuits, we can effectively design and analyze electrical circuits, ensuring proper distribution of voltage across components.
Is voltage split in a parallel circuit?
When it comes to understanding electrical circuits, one common question that often arises is whether voltage is split in a parallel circuit. In this section, we will explore the concept of voltage distribution in parallel circuits and clarify any misconceptions surrounding this topic.
Before diving into the specifics of voltage distribution in parallel circuits, let’s first establish what a parallel circuit is. In a parallel circuit, multiple components are connected side by side, allowing the current to flow through each component independently. This is in contrast to a series circuit, where the components are connected end to end, and the current flows through each component sequentially.
Explanation of voltage distribution in parallel circuits
In a parallel circuit, the voltage across each component remains the same. This means that the voltage across a resistor in parallel, for example, will be equal to the voltage across a capacitor or an inductor in parallel. This is due to the fact that the voltage across each component is determined by the voltage source connected to the circuit.
To understand why the voltage remains the same in a parallel circuit, let’s consider Kirchhoff’s voltage law. According to this law, the sum of the voltage drops across all components in a closed loop is equal to the voltage supplied by the source. In a parallel circuit, each component forms a separate loop, and the voltage drop across each component must add up to the total voltage supplied by the source.
Clarification on voltage splitting in series circuits, not parallel circuits
It is important to note that voltage splitting occurs in series circuits, not parallel circuits. In a series circuit, the total voltage supplied by the source is divided among the components based on their individual resistance. This results in different voltage drops across each component, with the sum of these voltage drops equaling the total voltage supplied.
In contrast, in a parallel circuit, the voltage across each component is the same, regardless of their individual resistance. This is because the components in a parallel circuit provide separate paths for the current to flow, allowing each component to have the same voltage drop.
Comparison of voltage distribution in parallel and series circuits
To further illustrate the difference in voltage distribution between parallel and series circuits, let’s consider a simple example. Imagine a circuit with two resistors connected in parallel and another circuit with the same two resistors connected in series.
In the parallel circuit, the voltage across each resistor will be the same, while in the series circuit, the voltage drop across each resistor will be different. This is because in a parallel circuit, the current is divided among the components, resulting in the same voltage drop across each component. In a series circuit, however, the current remains the same throughout the circuit, resulting in different voltage drops across each component.
To summarize, voltage is not split in a parallel circuit. Instead, the voltage across each component remains the same. This is due to the separate paths for current flow that parallel circuits provide, allowing each component to have the same voltage drop. In contrast, series circuits divide the total voltage among the components based on their individual resistance, resulting in different voltage drops across each component. Understanding these distinctions is crucial for comprehending the behavior of electrical circuits and designing efficient systems.
Is voltage the same across parallel circuits?
When it comes to understanding electrical circuits, one fundamental concept to grasp is the distribution of voltage. In parallel circuits, where multiple components are connected side by side, it is natural to wonder if the voltage remains the same across all the components. In this section, we will explore the behavior of voltage in parallel circuits and shed light on whether it remains consistent or not.
Explanation of voltage distribution in parallel circuits
In a parallel circuit, the components are connected across the same two points, forming multiple pathways for the current to flow. Each component in the circuit has its own voltage drop, which is the amount of voltage consumed by that specific component. However, despite these individual voltage drops, the total voltage across all the components in a parallel circuit remains the same.
To understand this better, let’s consider an analogy. Imagine a water pipe splitting into two branches, with each branch having a different resistance. The water pressure, analogous to voltage, will be the same at the beginning of each branch. Similarly, in a parallel circuit, the voltage across each component is the same at the points where they are connected.
Confirmation of voltage consistency across parallel circuits
The principle that voltage remains consistent across parallel circuits can be confirmed by applying Kirchhoff’s Voltage Law (KVL). KVL states that the sum of the voltage drops across all the components in a closed loop is equal to the applied voltage. In the case of parallel circuits, the applied voltage is the same across all the components, and therefore, the sum of the voltage drops across each component will also be equal to the applied voltage.
To illustrate this, let’s consider a simple parallel circuit with two resistors. If we apply a voltage of 12 volts across the circuit, each resistor will have a voltage drop of 12 volts. This means that the voltage across the first resistor will be 12 volts, and the voltage across the second resistor will also be 12 volts. Thus, the voltage remains consistent across parallel components.
Importance of voltage consistency in parallel circuit applications
The consistency of voltage across parallel components is crucial in various applications. One significant advantage is the ability to independently control each component in the circuit. Since the voltage across each component remains the same, it allows for precise control and manipulation of individual components without affecting the others.
Additionally, voltage consistency simplifies the analysis and calculations involved in designing parallel circuits. By knowing that the voltage across each component is the same, engineers can easily determine the values of resistors, capacitors, or inductors required to achieve the desired functionality.
Is voltage the same in parallel and series circuits?
When it comes to understanding electrical circuits, one of the fundamental concepts to grasp is voltage. Voltage is the potential difference between two points in a circuit and is often referred to as the “electric pressure” that pushes electrons through a circuit. In this article, we will explore the question: Is voltage the same in parallel and series circuits?
Comparison of voltage distribution in parallel and series circuits
To answer this question, let’s first compare how voltage is distributed in parallel and series circuits.
In a parallel circuit, multiple components are connected side by side, creating multiple paths for the current to flow. Each component in a parallel circuit has the same voltage across it. This means that the voltage across parallel components remains constant, regardless of the number of components connected. For example, if you have two resistors connected in parallel, each resistor will have the same voltage across it.
On the other hand, in a series circuit, components are connected end to end, forming a single path for the current to flow. The total voltage in a series circuit is divided among the components based on their resistance. This means that the voltage across each component in a series circuit can vary depending on its resistance. For instance, if you have two resistors connected in series, the voltage across each resistor will be different.
Explanation of voltage consistency in parallel circuits
The reason why voltage remains consistent across parallel components lies in Kirchhoff’s voltage law. According to this law, the sum of the voltage drops across all components in a closed loop is equal to the applied voltage. In a parallel circuit, each component forms a separate loop, allowing the voltage across each component to be the same.
Imagine a scenario where you have two resistors connected in parallel to a battery. Since the voltage across each resistor is the same, the current flowing through each resistor can be different. This is because the resistance of each resistor determines how much current will flow through it. So, while the voltage remains constant, the current can vary across parallel components.
Contrast with voltage division in series circuits
In contrast to parallel circuits, series circuits exhibit voltage division. The total voltage in a series circuit is divided among the components based on their resistance. This division of voltage is a result of the relationship between current, resistance, and voltage in Ohm’s Law (V = I * R).
Let’s consider a series circuit with two resistors. The total voltage across the circuit is equal to the sum of the voltage drops across each resistor. The voltage drop across each resistor is proportional to its resistance. Therefore, the resistor with a higher resistance will have a larger voltage drop, while the resistor with a lower resistance will have a smaller voltage drop.
To summarize, in a parallel circuit, the voltage across each component remains the same, while in a series circuit, the voltage is divided among the components based on their resistance.
In the next section, we will delve deeper into the concept of voltage division in series circuits and explore the mathematical calculations involved.
References
- Insert reference 1 here
- Insert reference 2 here
Why is voltage the same in parallel connection?
In electrical circuits, parallel connections play a crucial role in distributing voltage across various components. Understanding why voltage remains the same in parallel connections is essential for comprehending the behavior of these circuits. Let’s delve into the explanation, analysis, and importance of voltage consistency in parallel connections.
When components are connected in parallel, they share the same voltage across their terminals. This means that the potential difference across each component remains constant, regardless of the number of components connected. This fundamental principle is known as the voltage division rule.
Explanation of voltage distribution in parallel connections
To understand why voltage remains the same in parallel connections, we can turn to Kirchhoff’s Voltage Law (KVL). KVL states that the sum of the voltage drops across all components in a closed loop is equal to zero. In a parallel circuit, each component forms a separate loop, allowing us to analyze the voltage distribution across them individually.
Consider a simple parallel circuit with two resistors. Since the resistors are connected in parallel, they share the same voltage source. According to KVL, the sum of the voltage drops across the resistors must equal the voltage supplied by the source. Therefore, the voltage across each resistor is the same as the source voltage.
Analysis of voltage consistency in parallel connections
The concept of voltage consistency in parallel connections can be further understood by examining the behavior of other components, such as capacitors and inductors, in parallel circuits.
In a parallel circuit with capacitors, each capacitor stores charge independently. The voltage across each capacitor is determined by the amount of charge it stores and its capacitance. Since the voltage across each capacitor is the same, the total voltage across the parallel capacitors remains constant.
Similarly, in a parallel circuit with inductors, the voltage across each inductor is the same. This is because the rate of change of current through an inductor is directly proportional to the voltage across it. Therefore, in a parallel configuration, the voltage across each inductor remains consistent.
Importance of voltage consistency in parallel connections
The consistency of voltage in parallel connections is crucial for the proper functioning of electrical circuits. Here are a few reasons why voltage consistency is important:
-
Uniform operation: When components in a parallel circuit share the same voltage, they operate uniformly. This ensures that each component receives the necessary voltage to function optimally.
-
Balanced load: In parallel circuits, components with different resistances can be connected. By maintaining the same voltage across each component, the load is balanced, preventing any component from being overloaded.
-
Efficient power distribution: Parallel connections allow for efficient distribution of power. Since the voltage remains consistent across components, power can be distributed evenly, ensuring effective utilization of electrical energy.
Why is voltage the same everywhere in a parallel circuit?
In a parallel circuit, voltage remains the same across all components connected in parallel. This characteristic is essential to understand when analyzing and designing electrical circuits. Let’s delve into the reasons why voltage remains consistent in a parallel circuit and explore its significance.
Description of voltage distribution in parallel circuits
In a parallel circuit, multiple components are connected side by side, creating separate paths for current flow. Each component in the parallel circuit has its own voltage drop, which is the difference in voltage across the component. However, despite these individual voltage drops, the total voltage across all components remains the same.
To illustrate this, let’s consider a simple parallel circuit with two resistors. Each resistor has a specific voltage drop across it, but the total voltage across both resistors is the same as the voltage supplied by the source. This is a fundamental principle known as Kirchhoff’s voltage law, which states that the sum of the voltage drops in a closed loop is equal to the applied voltage.
Explanation of voltage consistency throughout a parallel circuit
The reason why voltage remains the same in a parallel circuit lies in the behavior of current. In a parallel circuit, the current splits and flows through each component independently. This means that the current passing through one component does not affect the current passing through another component.
Since voltage is directly proportional to current (according to Ohm’s law), the voltage drop across each component is determined by the current flowing through it and its resistance. However, the total voltage supplied by the source is divided among the components in such a way that the sum of the voltage drops across all components equals the source voltage.
Significance of voltage uniformity in parallel circuits
The consistent voltage across components in a parallel circuit has several practical implications. Here are a few key points:
-
Voltage division: The voltage division rule allows us to calculate the voltage across each component in a parallel circuit. By knowing the resistance values of the components, we can determine the voltage drop across each one, aiding in circuit analysis and design.
-
Equivalent voltage: In a parallel circuit, components with the same voltage rating can be connected together without any issues. This allows for flexibility in circuit design, as components can be easily added or removed without affecting the overall voltage.
-
Independent operation: Each component in a parallel circuit operates independently, meaning that if one component fails or is removed, the others continue to function unaffected. This redundancy can be advantageous in systems where reliability is crucial.
Is voltage the same in parallel capacitors?
Parallel capacitors are a common component in electronic circuits, and understanding how voltage is distributed across them is crucial for proper circuit design. In this section, we will explore the concept of voltage distribution in parallel capacitors and discuss its implications in electronic devices.
When capacitors are connected in parallel, they share the same voltage across their terminals. This means that the voltage across each capacitor in a parallel configuration is identical. Understanding this principle is essential for designing circuits that rely on the consistent distribution of voltage.
Explanation of voltage distribution in parallel capacitors
To understand why the voltage is the same in parallel capacitors, let’s delve into the underlying electrical principles. In a parallel circuit, the voltage across each component is determined by the voltage source connected to the circuit. Since capacitors store electrical energy, they resist changes in voltage. As a result, when capacitors are connected in parallel, they act as if they are a single capacitor with an increased capacitance.
When a voltage is applied to a parallel capacitor circuit, the charge distributes itself among the capacitors based on their capacitance values. The larger the capacitance of a capacitor, the more charge it can store. Consequently, the voltage across each capacitor remains the same because the charge distribution is proportional to the capacitance.
Confirmation of voltage consistency in parallel capacitor circuits
The principle of voltage consistency in parallel capacitors can be confirmed by applying Kirchhoff’s voltage law. According to this law, the sum of the voltage drops across all components in a closed loop is equal to the voltage supplied by the source.
In a parallel capacitor circuit, the voltage drop across each capacitor is the same, as discussed earlier. Therefore, the sum of the voltage drops across all the capacitors will be equal to the voltage supplied by the source. This confirms that the voltage is indeed consistent across parallel capacitors.
Application of parallel capacitors in electronic devices
The consistent voltage distribution in parallel capacitors makes them useful in various electronic devices. One common application is in power supply circuits, where parallel capacitors are used to filter out noise and stabilize voltage levels. By connecting capacitors of different capacitance values in parallel, designers can achieve the desired filtering effect and ensure a steady voltage output.
Parallel capacitors are also employed in audio circuits to improve the quality of sound reproduction. By strategically placing capacitors in parallel, engineers can create frequency-dependent voltage division, allowing specific frequencies to pass through while attenuating others. This technique, known as crossover design, enables the creation of high-quality audio systems with accurate sound reproduction.
Frequently Asked Questions
Why is the voltage the same in parallel circuits?
In parallel circuits, the voltage across each component is the same. This is because the voltage across each branch is determined by the voltage source connected to the circuit, and the branches in parallel share the same voltage source.
How is voltage the same in parallel combination?
In a parallel combination of components, such as resistors, capacitors, or inductors, the voltage across each component is the same. This is because the components are connected in parallel, and the voltage across parallel components is equal.
Is the voltage the same in parallel resistors?
Yes, the voltage is the same across resistors connected in parallel. In a parallel resistor configuration, the voltage across each resistor is equal to the total voltage supplied to the circuit.
Is the voltage the same across resistors in parallel?
Yes, in a parallel resistor configuration, the voltage across each resistor is the same. This is because the voltage across parallel components is equal.
Is the voltage split in a parallel circuit?
No, the voltage is not split in a parallel circuit. In a parallel circuit, the voltage across each branch or component is the same as the voltage supplied by the source.
Is the voltage the same across parallel circuits?
Yes, the voltage is the same across parallel circuits. In parallel circuits, the voltage across each branch or circuit is equal to the voltage supplied by the source.
Is the voltage the same in parallel and series?
No, the voltage is not the same in parallel and series circuits. In a series circuit, the voltage is divided among the components, whereas in a parallel circuit, the voltage across each component is the same.
Why is the voltage same in parallel connection?
The voltage is the same in a parallel connection because the components in parallel share the same voltage source. The voltage across each component is determined by the voltage source connected to the circuit.
Why is the voltage the same everywhere in a parallel circuit?
The voltage is the same everywhere in a parallel circuit because the components in parallel share the same voltage source. The voltage across each component is equal to the voltage supplied by the source.
Is the voltage the same in parallel capacitors?
Yes, the voltage is the same across capacitors connected in parallel. In a parallel capacitor configuration, the voltage across each capacitor is equal to the total voltage supplied to the circuit.

Hi……I am Kaushikee Banerjee completed my master’s in Electronics and Communications. I am an electronics enthusiast and am currently devoted to the field of Electronics and Communications. My interest lies in exploring cutting-edge technologies. I’m an enthusiastic learner and I tinker around with open-source electronics.