Modeling Potential Energy in Spring-Loaded Devices: A Comprehensive Guide

Modeling the potential energy in a spring-loaded device is a fundamental concept in physics, with applications ranging from mechanical engineering to sports equipment design. This comprehensive guide will delve into the intricacies of calculating spring potential energy, providing you with the necessary tools and techniques to master this essential skill.

Understanding Spring Potential Energy

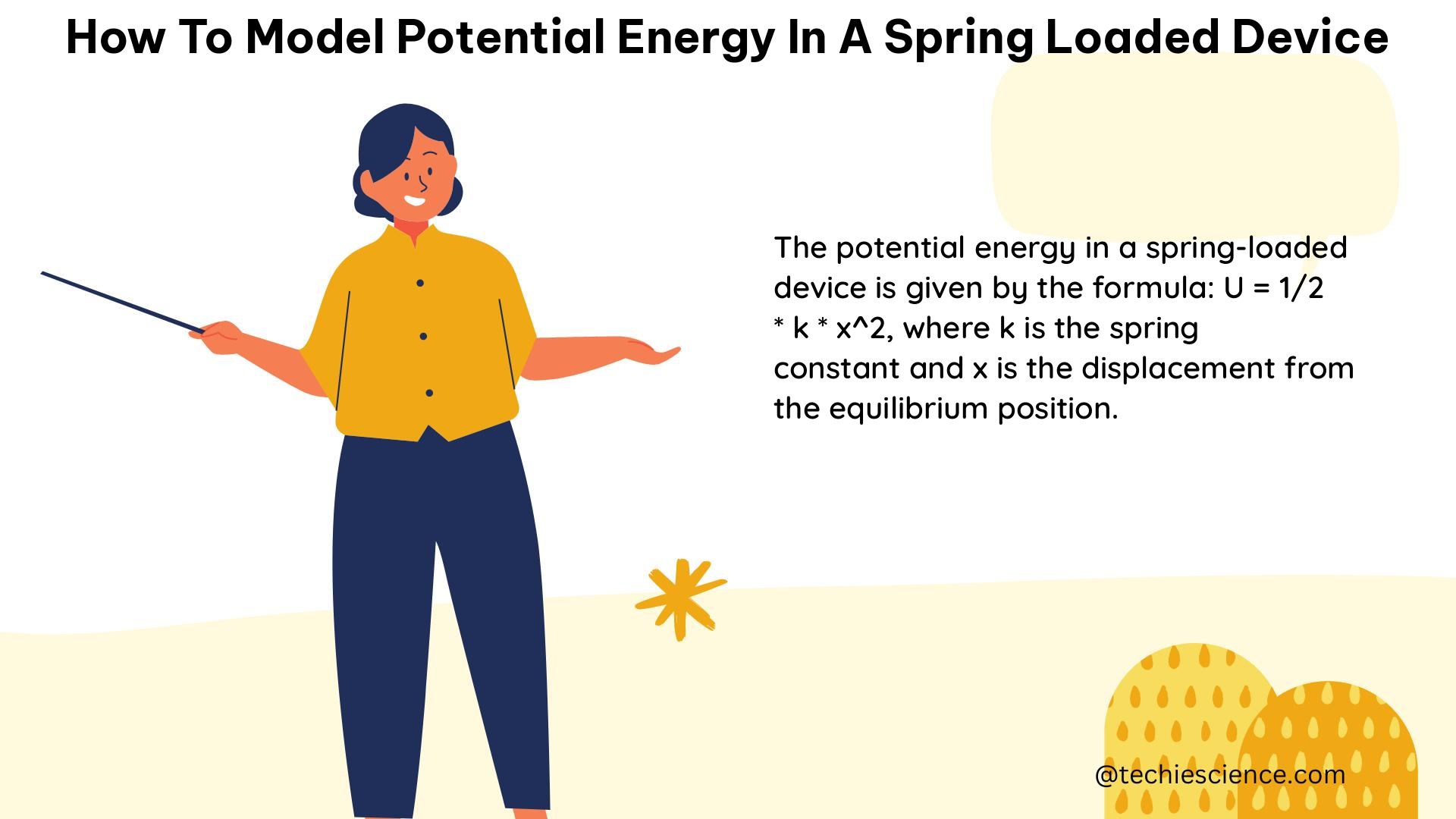
The potential energy stored in a spring-loaded device is directly related to the spring constant (k) and the distance the spring is compressed or stretched (Δx). The formula for calculating the spring potential energy (Uspring) is:

Uspring = 1/2 × k × Δx^2

Where:
– Uspring is the potential energy of the spring, measured in Joules (J)
– k is the spring constant, measured in Newtons per meter (N/m)
– Δx is the compressed or stretched distance of the spring from its normal position, measured in meters (m)

This formula is derived from the work-energy theorem, which states that the work done in compressing or stretching a spring is equal to the potential energy stored in the spring.

Determining the Spring Constant (k)

The spring constant (k) is a measure of the spring’s stiffness, where a more rigid spring has a larger spring constant. The spring constant can be determined through various methods, including:

1. Experimental Measurement: Attach one end of the spring to a fixed support and the other end to a mass. Measure the displacement of the spring under the weight of the mass and use the formula k = F/Δx, where F is the force applied (the weight of the mass) and Δx is the displacement.

2. Theoretical Calculation: For a simple spring with a uniform cross-section, the spring constant can be calculated using the formula k = (Ag)/L, where A is the cross-sectional area of the spring, g is the acceleration due to gravity, and L is the length of the spring.

3. Manufacturer Specifications: Many spring manufacturers provide the spring constant as part of the product specifications, making it easy to obtain this value.

It’s important to note that the spring constant may vary depending on the material, geometry, and other factors of the spring.

Calculating the Compressed or Stretched Distance (Δx)

The distance the spring is compressed or stretched (Δx) is the difference between the final position (xf) and the initial position (xi) of the spring. This can be measured directly using a ruler or other measurement device.

In some cases, the displacement may be given in terms of the applied force (F) and the spring constant (k) using Hooke’s law: F = k × Δx. Rearranging this equation, we can solve for the displacement: Δx = F/k.

Applying the Formula for Spring Potential Energy

Once you have determined the spring constant (k) and the compressed or stretched distance (Δx), you can use the formula Uspring = 1/2 × k × Δx^2 to calculate the potential energy stored in the spring.

For example, if a spring with a spring constant of 12 N/m is compressed 20 centimeters (or 0.2 meters), the spring potential energy is:

Uspring = 1/2 × 12 × 0.2^2 = 0.24 Joules

Therefore, the spring potential energy in this case is 0.24 Joules.

Advanced Considerations

1. Non-Linear Spring Behavior: In some cases, the spring may exhibit non-linear behavior, where the spring constant varies with the displacement. In such situations, the potential energy formula needs to be modified to account for the non-linear relationship between force and displacement.

2. Potential Energy Diagrams: Plotting the potential energy of a spring-loaded device as a function of the displacement can provide valuable insights into the system’s behavior, such as the equilibrium position and the stability of the system.

3. Energy Transformations: In a spring-loaded device, the potential energy stored in the spring can be converted into other forms of energy, such as kinetic energy or thermal energy, depending on the system’s design and the external forces acting on it.

4. Damping and Dissipation: Real-world spring-loaded devices often include damping mechanisms, such as friction or viscous forces, which can dissipate energy and affect the overall energy balance of the system.

Numerical Examples and Practice Problems

To solidify your understanding of modeling potential energy in spring-loaded devices, let’s work through some numerical examples and practice problems:

1. A spring with a spring constant of 20 N/m is compressed by 0.1 meters. Calculate the potential energy stored in the spring.

2. A mass of 2 kg is attached to a spring with a spring constant of 50 N/m. The mass is displaced 0.05 meters from its equilibrium position. Determine the potential energy stored in the spring.

3. A spring-loaded device is used to launch a projectile. The spring has a spring constant of 80 N/m and is compressed 0.15 meters. Calculate the potential energy stored in the spring and the maximum height the projectile can reach (assuming no air resistance).

4. A compression spring with a spring constant of 30 N/m is used in a shock absorber system. If the spring is compressed by 0.08 meters, find the potential energy stored in the spring.

5. A torsional spring with a spring constant of 0.5 N⋅m/rad is used in a door hinge. If the spring is twisted by 0.2 radians, calculate the potential energy stored in the spring.

Remember to show your work and provide the final answers with the appropriate units.

Conclusion

Modeling the potential energy in spring-loaded devices is a crucial skill in physics and engineering. By understanding the relationship between the spring constant, the displacement, and the potential energy, you can effectively analyze and design a wide range of spring-loaded systems, from mechanical devices to sports equipment.

This comprehensive guide has provided you with the necessary tools and techniques to master the art of calculating spring potential energy. Remember to practice the concepts and examples presented here to solidify your understanding and apply these principles to real-world problems.

Reference:

1. How to Calculate the Spring Potential Energy of an Object
2. Spring Force and Energy
3. How to Calculate the Potential and Kinetic Energy in a Spring
4. Potential Energy of a Spring
5. Hooke’s Law and Spring Potential Energy