The kinetic theory of gases provides a fundamental understanding of the behavior of gas molecules, which is crucial for measuring their velocity. This comprehensive guide will delve into the intricacies of using the kinetic theory to determine the root mean square (RMS) velocity of gas molecules, as well as explore the relationship between velocity, pressure, volume, and temperature through the ideal gas law.
Understanding the Kinetic Theory of Gases
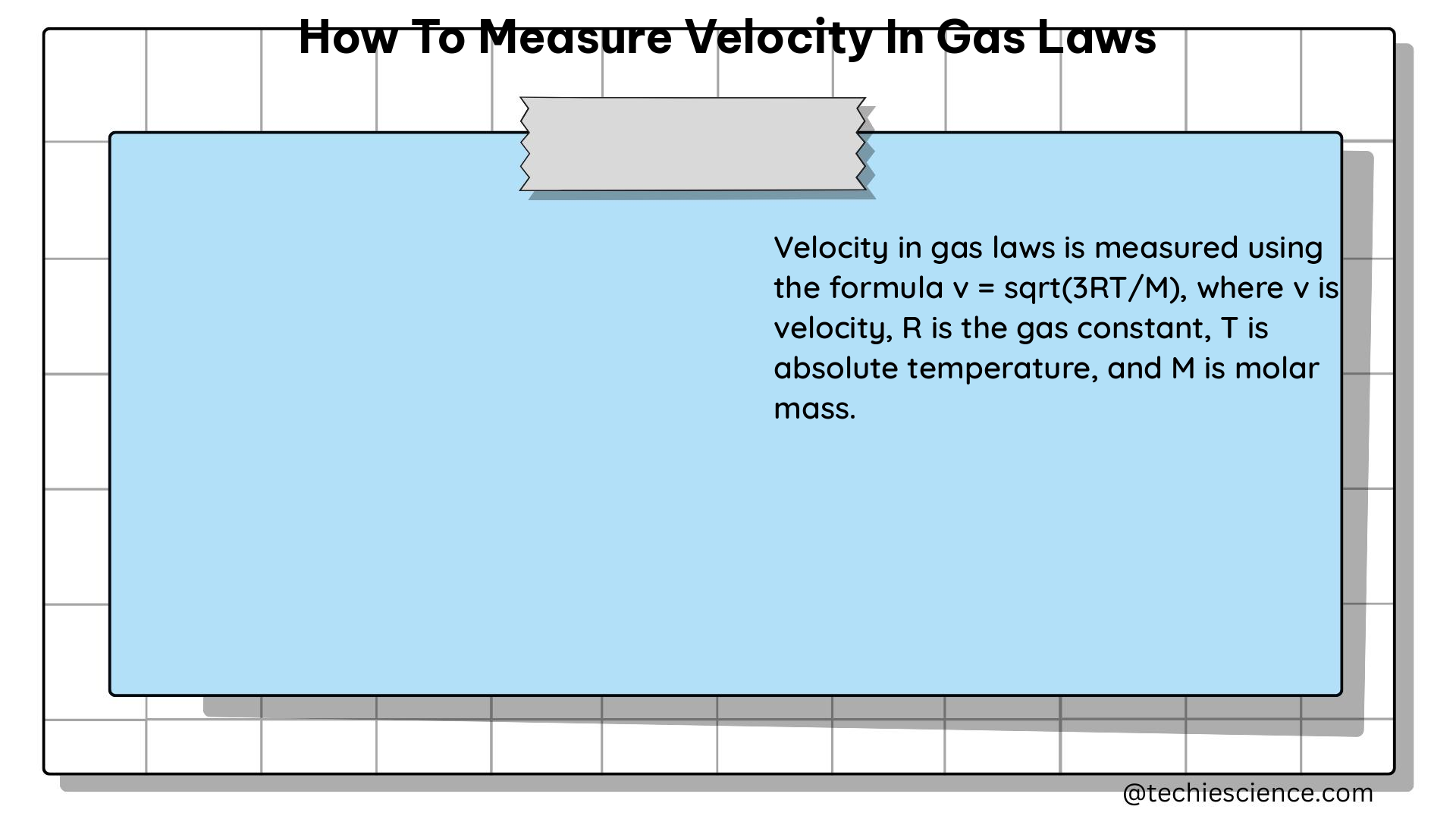
The kinetic theory of gases states that gas molecules are in constant random motion, and their kinetic energy is directly proportional to the temperature of the gas. This theory allows us to derive an equation for the RMS velocity of gas molecules, which is given by:
v = √(3RT/M)
where:
– v is the RMS velocity of the gas molecules
– R is the universal gas constant (8.314 J/mol·K)
– T is the temperature of the gas (in Kelvin)
– M is the molar mass of the gas (in kg/mol)
To measure the velocity of gas molecules, we need to know the temperature and molar mass of the gas. Let’s explore this in more detail.
Measuring Temperature and Molar Mass
Measuring Temperature
The temperature of the gas can be measured using a thermometer. It’s important to ensure that the thermometer is properly calibrated and placed in the gas sample to obtain an accurate reading. The temperature must be measured in Kelvin, as this is the unit required in the RMS velocity equation.
Measuring Molar Mass
The molar mass of the gas can be found using the periodic table. Each element has a specific molar mass, which can be used to calculate the molar mass of a compound. For example, the molar mass of oxygen (O2) is approximately 32.0 g/mol or 0.032 kg/mol.
Calculating the RMS Velocity
Once we have the temperature and molar mass of the gas, we can plug these values into the RMS velocity equation and solve for the velocity.
For example, let’s consider a sample of oxygen gas (O2) at a temperature of 300K. We can calculate the RMS velocity as follows:
v = √(3RT/M)
v = √(3 × 8.314 J/mol·K × 300K / 0.032 kg/mol)
v = 484 m/s
Therefore, the RMS velocity of O2 molecules at 300K is approximately 484 m/s.
It’s important to note that the RMS velocity is an average value, and individual gas molecules may have higher or lower velocities. However, the RMS velocity provides a useful measure of the overall motion of gas molecules.
Relationship between Velocity, Pressure, Volume, and Amount
In addition to the RMS velocity, we can also measure other measurable quantities of gases, such as pressure, volume, and amount. These quantities are related to each other through the ideal gas law, which states that the pressure of a gas is directly proportional to its temperature, volume, and amount.
The ideal gas law is given by the equation:
PV = nRT
where:
– P is the pressure of the gas
– V is the volume of the gas
– n is the amount of the gas (in moles)
– R is the universal gas constant (8.314 J/mol·K)
– T is the temperature of the gas (in Kelvin)
By measuring the pressure, volume, and temperature of a gas, we can use the ideal gas law to calculate the amount of the gas present. Conversely, if we know the amount of the gas and its temperature and volume, we can use the ideal gas law to calculate the pressure.
Units and Conversions
When measuring the velocity of gas molecules, it’s important to use the correct units for temperature, pressure, and volume. In the SI system, the unit for temperature is the Kelvin, the unit for pressure is the pascal (Pa), and the unit for volume is the cubic meter (m³).
However, in many chemical and engineering applications, it’s more common to use the unit of atmospheres (atm) for pressure and liters (L) for volume. To convert between these units, we can use the following conversion factors:
- 1 atmosphere (atm) = 101,325 pascals (Pa)
- 1 liter (L) = 0.001 cubic meters (m³)
By using the correct units and conversion factors, we can ensure accurate measurements and calculations when working with gas laws and velocities.
Practical Applications and Examples
The ability to measure the velocity of gas molecules has numerous practical applications in various fields, such as:
- Thermodynamics: Calculating the kinetic energy and temperature of gas systems.
- Fluid Dynamics: Analyzing the flow and behavior of gases in engineering applications.
- Astrophysics: Studying the motion and properties of gases in astronomical phenomena.
- Chemical Reactions: Understanding the collision dynamics and reaction rates of gas-phase reactions.
- Atmospheric Science: Modeling the behavior of gases in the Earth’s atmosphere.
Here’s an example of how to apply the RMS velocity equation:
Suppose we have a sample of helium gas (He) at a temperature of 400K. The molar mass of helium is 4.003 g/mol or 0.004003 kg/mol. Calculate the RMS velocity of the helium gas molecules.
v = √(3RT/M)
v = √(3 × 8.314 J/mol·K × 400K / 0.004003 kg/mol)
v = 1,307 m/s
Therefore, the RMS velocity of helium gas molecules at 400K is approximately 1,307 m/s.
Conclusion
Measuring the velocity of gas molecules is a fundamental aspect of understanding the behavior of gases. By using the kinetic theory of gases and the ideal gas law, we can determine the RMS velocity of gas molecules, as well as their relationship to other measurable quantities, such as pressure, volume, and amount.
This comprehensive guide has provided you with the necessary knowledge and tools to measure the velocity of gas molecules effectively. Remember to always use the correct units and conversion factors, and apply the principles of the kinetic theory and ideal gas law to your specific gas systems and applications.
References
- Non-Ideal Gases and the Van der Waals Equation – YouTube. Retrieved from https://www.youtube.com/watch?v=8zJrjEV9n8o
- Measurable Quantities of Gases – Chemistry LibreTexts. Retrieved from https://chem.libretexts.org/Courses/Heartland_Community_College/CHEM_120:_Fundamentals_of_Chemistry/06:_Gases/6.02:_Measurable_Properties_of_Gases
- Demonstrating the Relationship between Pressure, Number of Molecules, and Velocity – Study.com. Retrieved from https://study.com/skill/learn/demonstrating-the-relationship-between-pressure-number-of-molecules-and-velocity-explanation.html
- Measurable Quantity – an overview | ScienceDirect Topics. Retrieved from https://www.sciencedirect.com/topics/engineering/measurable-quantity
- Gas Velocity – ChemTeam. Retrieved from https://www.chemteam.info/GasLaw/gas-velocity.html

The lambdageeks.com Core SME Team is a group of experienced subject matter experts from diverse scientific and technical fields including Physics, Chemistry, Technology,Electronics & Electrical Engineering, Automotive, Mechanical Engineering. Our team collaborates to create high-quality, well-researched articles on a wide range of science and technology topics for the lambdageeks.com website.
All Our Senior SME are having more than 7 Years of experience in the respective fields . They are either Working Industry Professionals or assocaited With different Universities. Refer Our Authors Page to get to know About our Core SMEs.