How To Find Velocity With Constant Acceleration: Problems And Examples

Velocity is a fundamental concept in physics that measures the rate of change of an object’s position with respect to time. When an object experiences constant acceleration, the process of finding its velocity becomes a bit more complex. In this blog post, we will explore the topic of how to find velocity with constant acceleration. We will discuss the formula for velocity with constant acceleration, step-by-step guides on how to use the formula, and provide worked-out examples. Additionally, we will also cover how to find constant acceleration with velocity and time, as well as how to calculate the final velocity with constant acceleration.

How to Calculate Velocity with Constant Acceleration

The Formula for Velocity with Constant Acceleration

To calculate velocity with constant acceleration, we can use the following formula:

$v = u + at$

Where:
– $v$ represents the final velocity of the object.
– $u$ represents the initial velocity of the object.
– $a$ represents the constant acceleration of the object.
– $t$ represents the time interval during which the velocity changes.

Step-by-step Guide on How to Use the Formula

To use the formula for velocity with constant acceleration, follow these steps:

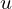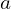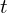Identify the values for $u$ , $a$ , and $t$ in the given problem.
Substitute the values into the formula: $v = u + at$ .
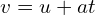Calculate the product of 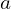$a$ and $t$ .
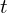Add the product to the initial velocity $u$ .
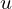The result is the final velocity $v$ .

Worked out Examples

Let’s take a look at a couple of examples to further illustrate how to calculate velocity with constant acceleration.

Example 1:
A car starts from rest and accelerates at a rate of 2 m/s^2 for a time interval of 5 seconds. What is its final velocity?

Here, we are given:
$u = 0 , m/s$ (initial velocity)
$a = 2 , m/s^2$ (constant acceleration)
$t = 5 , s$ (time interval)

Using the formula $v = u + at$ , we can substitute the values and calculate the final velocity:
$v = 0 + (2 , m/s^2)(5 , s)$
$v = 0 + 10 , m/s$
$v = 10 , m/s$

Therefore, the final velocity of the car is 10 m/s.

Example 2:
A ball is thrown upwards with an initial velocity of 15 m/s. It experiences a constant acceleration due to gravity of -9.8 m/s^2. What is its final velocity after 2 seconds?

Here, we are given:
$u = 15 , m/s$ (initial velocity)
$a = -9.8 , m/s^2$ (constant acceleration)
$t = 2 , s$ (time interval)

Using the formula $v = u + at$ , we can substitute the values and calculate the final velocity:
$v = 15 + (-9.8 , m/s^2)(2 , s)$
$v = 15 + (-19.6 , m/s)$
$v = -4.6 , m/s$

Therefore, the final velocity of the ball after 2 seconds is -4.6 m/s.

How to Find Constant Acceleration with Velocity and Time

The Formula for Finding Constant Acceleration

To find the constant acceleration when given the initial velocity, final velocity, and time interval, we can use the following formula:

$a = frac{v - u}{t}$

Where:
– $a$ represents the constant acceleration of the object.
– $v$ represents the final velocity of the object.
– $u$ represents the initial velocity of the object.
– $t$ represents the time interval during which the velocity changes.

Detailed Steps on How to Use the Formula

To find the constant acceleration using the formula, follow these steps:

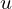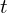Identify the values for $v$ , $u$ , and $t$ in the given problem.
Substitute the values into the formula: $a = frac{v - u}{t}$ .
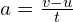Calculate the difference between $v$ and $u$ .
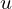Divide the difference by $t$ .
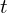The result is the constant acceleration $a$ .

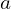Practical Examples

Let’s work through a couple of examples to demonstrate how to find constant acceleration with velocity and time.

Example 1:
A train starts from rest and reaches a velocity of 30 m/s in 10 seconds. What is its constant acceleration?

Here, we are given:
$u = 0 , m/s$ (initial velocity)
$v = 30 , m/s$ (final velocity)
$t = 10 , s$ (time interval)

Using the formula $a = frac{v - u}{t}$ , we can substitute the values and calculate the constant acceleration:
$a = frac{30 - 0}{10}$
$a = frac{30}{10}$
$a = 3 , m/s^2$

Therefore, the constant acceleration of the train is 3 m/s^2.

Example 2:
A rocket traveling at 100 m/s decelerates uniformly and comes to a stop in 5 seconds. What is its constant acceleration?

Here, we are given:
$u = 100 , m/s$ (initial velocity)
$v = 0 , m/s$ (final velocity)
$t = 5 , s$ (time interval)

Using the formula $a = frac{v - u}{t}$ , we can substitute the values and calculate the constant acceleration:
$a = frac{0 - 100}{5}$
$a = frac{-100}{5}$
$a = -20 , m/s^2$

Therefore, the constant acceleration of the rocket is -20 m/s^2.

How to Calculate Final Velocity with Constant Acceleration

The Formula for Final Velocity with Constant Acceleration

how to find velocity with constant acceleration — Image by P. Fraundorf – Wikimedia Commons, Licensed under CC BY-SA 4.0.

To calculate the final velocity of an object with constant acceleration, we can use the following formula:

$v = u + 2as$

Where:
– $v$ represents the final velocity of the object.
– $u$ represents the initial velocity of the object.
– $a$ represents the constant acceleration of the object.
– $s$ represents the displacement of the object.

Step-by-step Guide on How to Use the Formula

To use the formula for final velocity with constant acceleration, follow these steps:

Identify the values for 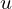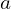$u$ , $a$ , and $s$ in the given problem.
Substitute the values into the formula: $v = u + 2as$ .
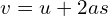Calculate the product of 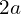$2a$ and $s$ .
Add the product to the initial velocity $u$ .
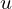The result is the final velocity $v$ .

Worked out Examples

Let’s look at a couple of examples to demonstrate how to calculate the final velocity with constant acceleration.

Example 1:
A car accelerates from rest at a rate of 4 m/s^2 for a distance of 100 meters. What is its final velocity?

Here, we are given:
$u = 0 , m/s$ (initial velocity)
$a = 4 , m/s^2$ (constant acceleration)
$s = 100 , m$ (displacement)

Using the formula $v = u + 2as$ , we can substitute the values and calculate the final velocity:
$v = 0 + 2(4 , m/s^2)(100 , m)$
$v = 0 + 800 , m/s$
$v = 800 , m/s$

Therefore, the final velocity of the car is 800 m/s.

Example 2:
A ball is dropped from a height of 50 meters. It accelerates uniformly at a rate of 9.8 m/s^2. What is its final velocity?

Here, we are given:
$u = 0 , m/s$ (initial velocity)
$a = 9.8 , m/s^2$ (constant acceleration)
$s = -50 , m$ (displacement)

Using the formula $v = u + 2as$ , we can substitute the values and calculate the final velocity:
$v = 0 + 2(9.8 , m/s^2)(-50 , m)$
$v = 0 + (-980 , m/s)$
$v = -980 , m/s$

Therefore, the final velocity of the ball is -980 m/s.

In this blog post, we discussed how to find velocity with constant acceleration. We explored the formula for velocity with constant acceleration, step-by-step guides on how to use the formula, and provided worked-out examples. We also covered how to find constant acceleration with velocity and time, as well as how to calculate the final velocity with constant acceleration. By understanding these concepts and formulas, you can effectively analyze and solve problems involving objects in motion with constant acceleration.

How can the concept of finding velocity with constant acceleration be used to explore the idea of Finding constant acceleration with distance?

The concept of finding velocity with constant acceleration involves determining the rate at which an object’s velocity changes over time. Similarly, in the idea of Finding constant acceleration with distance, the focus is on determining the acceleration of an object based on the distance it travels. By bridging these two themes, we can explore how the relationship between velocity, acceleration, distance, and time can be used to find constant acceleration when both distance and time are known. This understanding deepens our ability to analyze and interpret the motion of objects in various physical scenarios.

Numerical Problems on how to find velocity with constant acceleration

Problem 1:

A car accelerates from rest at a constant rate of 2 m/s² for a time of 5 seconds. Find the final velocity of the car.

Solution:

Given:
Initial velocity, $u = 0$ m/s
Acceleration, $a = 2$ m/s²
Time, $t = 5$ s

We can use the formula for velocity with constant acceleration:

$v = u + at$

Substituting the given values:

$v = 0 + (2)(5)$

Simplifying:

$v = 0 + 10$

Therefore, the final velocity of the car is $v = 10$ m/s.

Problem 2:

A train decelerates at a constant rate of 3 m/s² until it comes to a stop. If the initial velocity of the train is 20 m/s, how long will it take for the train to stop?

Solution:

Given:
Initial velocity, $u = 20$ m/s
Acceleration, $a = -3$ m/s² (negative sign indicates deceleration)
Final velocity, $v = 0$ m/s

We can use the formula for velocity with constant acceleration:

$v = u + at$

Substituting the given values:

$0 = 20 + (-3)t$

Simplifying:

$-3t = -20$

Dividing both sides by -3:

$t = frac{-20}{-3}$

Therefore, it will take the train approximately $t approx 6.67$ seconds to come to a stop.

Problem 3:

A rocket accelerates uniformly from rest at a rate of 10 m/s² for a distance of 500 meters. Find the final velocity of the rocket.

Solution:

Given:
Initial velocity, $u = 0$ m/s
Acceleration, $a = 10$ m/s²
Distance, $s = 500$ m

We can use the formula for final velocity with constant acceleration:

$v^2 = u^2 + 2as$

Substituting the given values:

$v^2 = (0)^2 + 2(10)(500)$

Simplifying:

$v^2 = 0 + 10000$

Taking the square root of both sides:

$v = sqrt{10000}$

Therefore, the final velocity of the rocket is $v = 100$ m/s.

Also Read:

Keerthi Murthi

I am Keerthi K Murthy, I have completed post graduation in Physics, with the specialization in the field of solid state physics. I have always consider physics as a fundamental subject which is connected to our daily life. Being a science student I enjoy exploring new things in physics. As a writer my goal is to reach the readers with the simplified manner through my articles.