How to Find Velocity Ratio: A Comprehensive Guide for Physics Students

Summary

Velocity ratio, also known as mechanical advantage, is a crucial concept in physics that describes the relationship between the input and output velocities of a mechanical system. This comprehensive guide will provide you with a deep understanding of the principles, formulas, and practical applications of velocity ratio, equipping you with the knowledge to solve complex problems in physics.

Understanding Velocity Ratio

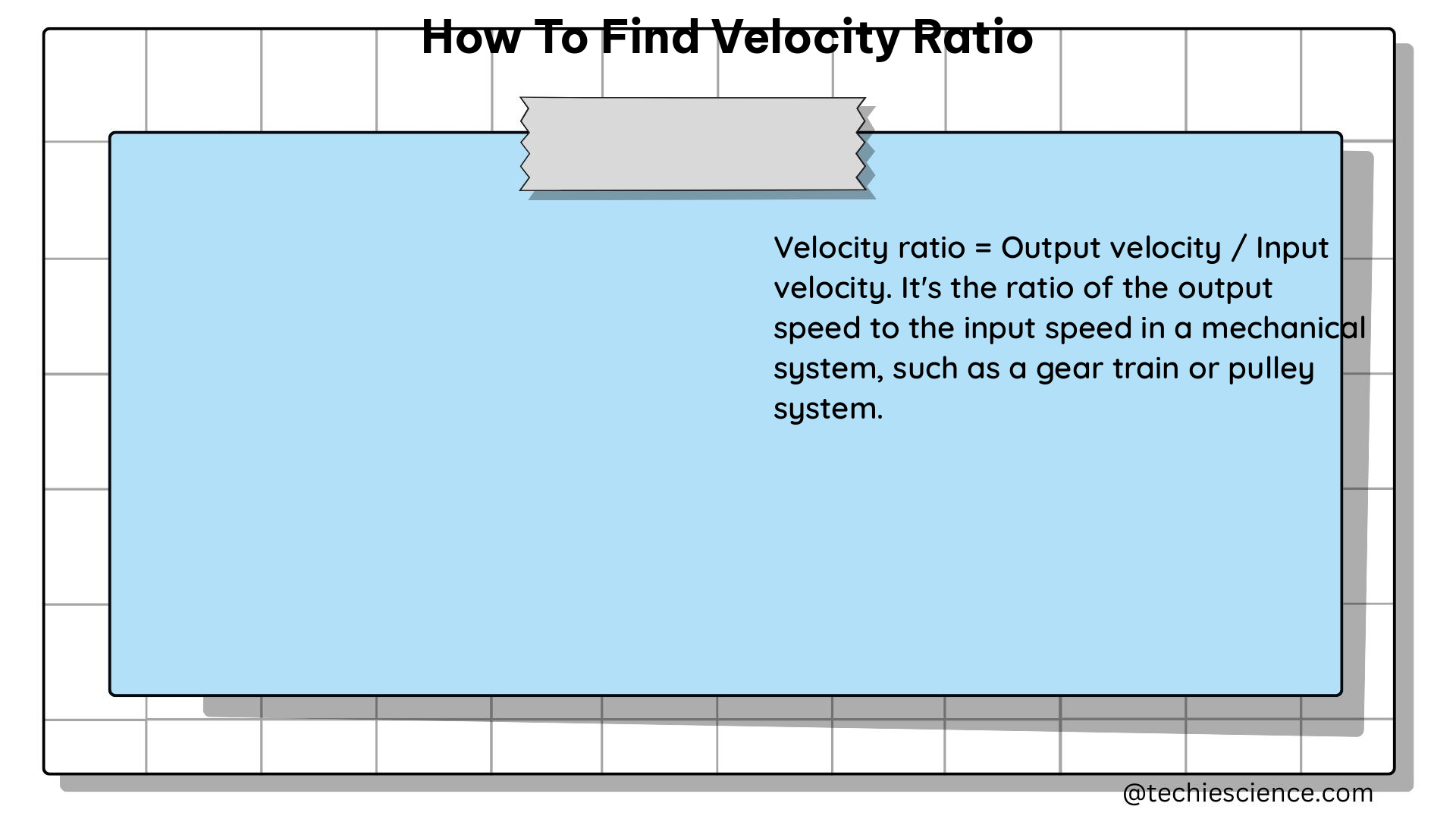
Velocity ratio, denoted as VR, is the ratio of the output velocity to the input velocity of a mechanical system. It is a dimensionless quantity that represents the theoretical speed increase or decrease achieved by the system. The velocity ratio is directly related to the mechanical advantage (MA) and the efficiency (η) of the system, as shown by the following formula:

Velocity Ratio (VR) = Mechanical Advantage (MA) / Efficiency (η) × 100

The mechanical advantage is the ratio of the load (output force) to the effort (input force) applied to the system, and the efficiency is the ratio of the output power to the input power, usually expressed as a percentage.

Calculating Velocity Ratio

To calculate the velocity ratio of a mechanical system, you can follow these steps:

1. Determine the Mechanical Advantage (MA): The mechanical advantage is the ratio of the load (output force) to the effort (input force) applied to the system. It can be calculated using the formula:

Mechanical Advantage (MA) = Load / Effort

For example, if a load of 400 Newtons is being lifted by an effort of 300 Newtons, the mechanical advantage would be:

MA = 400 N / 300 N = 1.33

1. Determine the Efficiency (η): The efficiency of a mechanical system is the ratio of the output power to the input power, usually expressed as a percentage. The efficiency can be measured experimentally or obtained from the system’s specifications.

2. Calculate the Velocity Ratio (VR): Once you have the mechanical advantage and the efficiency, you can calculate the velocity ratio using the formula:

Velocity Ratio (VR) = Mechanical Advantage (MA) / Efficiency (η) × 100

Continuing the previous example, if the efficiency of the system is 66.5%, the velocity ratio would be:

VR = 1.33 / 0.665 × 100 = 200%

This means that the output velocity is twice the input velocity, or the system has a 200% velocity ratio.

Velocity Ratio in Pulley Systems

In the context of pulley systems, the velocity ratio can be calculated as the number of rope segments or wheels in the system. This is because the output velocity is directly proportional to the number of rope segments or wheels.

For instance, in a simple pulley system with one wheel, the velocity ratio is 1, meaning the output velocity is the same as the input velocity. In a system with two wheels, the velocity ratio is 2, and in a system with three wheels, the velocity ratio is 3, and so on.

The general formula for the velocity ratio of a pulley system is:

Velocity Ratio (VR) = Number of Rope Segments or Wheels

This formula assumes that the system is frictionless and the rope or cable is inextensible.

Factors Affecting Velocity Ratio

The velocity ratio of a mechanical system can be affected by various factors, including:

1. Friction: Friction in the system can reduce the efficiency and, consequently, the velocity ratio. Higher friction leads to a lower velocity ratio.

2. Inertia: The inertia of the moving parts in the system can also affect the velocity ratio, especially during acceleration or deceleration.

3. Elasticity: If the rope or cable in a pulley system is not completely inextensible, it can affect the velocity ratio.

4. Mechanical Losses: Other mechanical losses, such as bearing losses, gear losses, and energy dissipation, can also contribute to a lower velocity ratio.

To account for these real-world factors, it is often more useful to calculate the efficiency of the system, which takes into account the actual performance of the system.

Practical Applications of Velocity Ratio

Velocity ratio is an important concept in various engineering applications, including:

1. Mechanical Advantage: Velocity ratio is directly related to the mechanical advantage of a system, which is crucial in the design of machines and devices that need to amplify force or torque, such as levers, pulleys, and gears.

2. Power Transmission: Velocity ratio is essential in the design of power transmission systems, such as those found in automobiles, industrial machinery, and robotics, where the goal is to transmit power efficiently while maintaining the desired speed and torque characteristics.

3. Mechanical Advantage Calculations: Velocity ratio is used to calculate the mechanical advantage of a system, which is important in the design and analysis of various mechanical devices, such as cranes, hoists, and winches.

4. Efficiency Optimization: Understanding the relationship between velocity ratio and efficiency can help engineers optimize the performance of mechanical systems by balancing the trade-offs between speed, force, and energy consumption.

5. Predictive Maintenance: Monitoring changes in the velocity ratio of a mechanical system can be used as a diagnostic tool for predictive maintenance, as it can indicate the onset of problems, such as wear, misalignment, or bearing failure.

Numerical Examples

1. Example 1: A simple pulley system has a load of 500 N and an effort of 300 N. The efficiency of the system is 80%. Calculate the velocity ratio.

Given:
– Load = 500 N
– Effort = 300 N
– Efficiency (η) = 80%

Step 1: Calculate the mechanical advantage (MA).
MA = Load / Effort
MA = 500 N / 300 N = 1.67

Step 2: Calculate the velocity ratio (VR).
VR = MA / η × 100
VR = 1.67 / 0.80 × 100 = 208.75%

1. Example 2: A compound pulley system has 3 wheels. Assuming the system is frictionless and the rope is inextensible, calculate the velocity ratio.

Given:
– Number of wheels = 3

Step 1: Calculate the velocity ratio (VR) using the formula for pulley systems.
VR = Number of rope segments or wheels
VR = 3

Therefore, the velocity ratio of the compound pulley system with 3 wheels is 3.

1. Example 3: A mechanical system has a load of 800 N and an effort of 400 N. The efficiency of the system is 75%. Calculate the velocity ratio.

Given:
– Load = 800 N
– Effort = 400 N
– Efficiency (η) = 75%

Step 1: Calculate the mechanical advantage (MA).
MA = Load / Effort
MA = 800 N / 400 N = 2

Step 2: Calculate the velocity ratio (VR).
VR = MA / η × 100
VR = 2 / 0.75 × 100 = 266.67%

These examples demonstrate the step-by-step process of calculating the velocity ratio of various mechanical systems, considering the mechanical advantage and the efficiency of the system.

Conclusion

Velocity ratio is a fundamental concept in physics that describes the relationship between the input and output velocities of a mechanical system. By understanding the principles, formulas, and practical applications of velocity ratio, you can effectively analyze and design mechanical systems, optimize their performance, and solve complex problems in physics. This comprehensive guide has provided you with the necessary knowledge and tools to become proficient in finding the velocity ratio of various mechanical systems.

References

1. Ratio Scales | Definition, Examples, & Data Analysis – Scribbr
2. How to calculate and improve inventory velocity in eCommerce
3. Velocity Ratio and its Application to Predicting Velocities – USGS
4. Calculate Velocity Ratio and Efficiency of a Pulley in Physics – YouTube
5. How to calculate velocity ratio, input and output speed – YouTube